Introduction
Institutional scholars have widely documented that institutions, as the shared rules, norms, strategies, and values that shape human decision making (North 1990), influence natural resource management. The institutions in a given system can shape whether resource management will be successful or not (Ostrom et al. 1994). In cases where natural resource management is deemed unsuccessful, people often seek to change the institutions governing that system (Burger et al. 2001; Ostrom 1990). Understanding how institutions change is a topic rife with difficulties, including observing change over long time scales, different theories about the mechanism of change, and analysis and measurement (Campbell 2004). In this paper, we present a theoretically driven agent-based model (ABM) examining institutional change in a social-ecological system grappling with management of an invasive plant, comparing theoretical perspectives of institutional change with empirical data on management efforts. A better understanding of which theories of institutional change are consistent with empirical data can lead to new theoretical insights just as when empirical studies of cooperative resource management confronted the tragedy of the commons (Janssen & Ostrom 2006).
Many institutional studies of common pool and natural resources have focused on operationalizing the role of rules in management decisions (Helmke & Levitsky 2004; Raiser 1997), but here we examine strategies and norms associated with the management of an invasive plant. We differentiate rules, norms, and strategies in terms of the institutional grammar, using the ADICO syntax (Crawford & Ostrom, 1995). In this syntax, A represents the attributes of an actor to which an institution applies (e.g. gender, education, experience); D represents the deontic logic operators may/must/must not; I represents the aIm or actions to which the deontic applies; C represents the conditions under which the aim is permitted; and O is the “or else” representing sanctions for deviating from a rule. Strategies contain the elements AIC, norms include ADIC, and rules are the most precise, written as ADICO. In practice, the boundaries between strategies and norms or norms and rules may be blurred (Crawford & Ostrom, 1995). In the background section, we explain why we categorize institutions related to invasive plant management in our model as strategies and norms using the ADICO syntax. Examining shared strategies and norms for natural resource management is relevant to understanding management outcomes, especially in decentralized situations. In decentralized cases, where local communities are responsible for natural resource management, there may be less emphasis on rules (including laws and policies) and more emphasis on social norms (Ostrom 2005).
Studies of successful common pool resource management are often case-study based and rely upon analysis of rich qualitative data. More recently, the field has focused on incorporating complementary quantitative data and computational analysis with qualitative data. Advances in the area of computational social science have made agent-based (also known as individual-based in ecology) models increasingly appealing to study natural resources and social-ecological systems (SES) (Bonabeau 2002; Heard et al. 2015). Such computational models provide researchers the opportunity to manipulate a wide variety of system characteristics to construct counterfactual situations, reevaluate past conditions, or explore the impact of added factors that cannot be or are difficult to directly observe. In this sense, agent-based models have been described as virtual laboratories for exploring social-ecological systems (Magliocca et al. 2015). Our agent-based model explores two theoretical perspectives of institutional change (rational choice and cultural diffusion) to understand which perspective better explains empirical data on strategies and norms used to manage an invasive plant in locally governed forests, known as community forests, in Chitwan, Nepal.
Invasive species represent one type of challenge facing social-ecological systems and are often interconnected with or exacerbated by other issues such as urbanization, climate change, and environmental pollution (Keller et al. 2014). Invasive species are most frequently studied in the context of their ecological or economic, but not social, impacts (Rai & Scarborough 2015; Schuettler et al. 2011). Yet it is recognized that it is important to understand invasive species’ social and ecological effects (Atlan & Darrot 2012). Without an understanding of how invasive plants impact both the social and ecological subsystems, management attempts may be contentious among social groups with different interests and values (Epanchin-Niell et al. 2010; Estevez et al. 2015) or ineffective due to poor understanding of the institutions that interact with management efforts. Murphy et al. (2013) find that future Mikania management efforts in Chitwan should incorporate plans to reduce burning and to introduce information about best practices. Successful implementation of these recommendations requires a detailed understanding of the social context, including institutions.
The primary objective of this study is to compare two theories of institutional change, rational choice and cultural diffusion, to understand which better fits empirical observations of Mikania management strategies and norms in Chitwan. Two secondary aims are: to test the hypothesis that higher initial percentages of agents adopting the best practice removal method will reduce Mikania (even with burning occurring) and to analyze the effect of the initial percentage of Mikania present. Our agent-based modeling approach adds value to this human-environment research, including acting as a platform to address uncertainty (for example, our analysis of different scenarios of strategy and norm adoption). The ABM allows us to perform theory-based experiments (what-if tests) to understand which parameters influence model outcomes and provides interesting insights into future research avenues.
Next, we present the details of the study site and literature related to institutional change that inform our model. We then provide the model conceptualization and overview, and results from the rational choice and cultural diffusion sub-models. The subsequent discussion identifies areas for further research based on the results, including empirical studies of the initial amount of Mikania removal and comparison of additional theories of institutional change.
Background
Study site
Chitwan, Nepal is a district located in southern Nepal, in the sub-tropical Terai region. The Terai is one of Nepal’s five physiographic regions and was historically densely forested. However, much deforestation has occurred in the nineteenth century and forested areas continue to decline at an annual rate of approximately 1.7 percent (Bhuju et al. 2007). Forests cover approximately 30 percent of the region, with other areas composed of wetlands, tall grasslands, and scrub savannah (Bhuju et al. 2007). Chitwan has been home to community forest user groups since the program was formalized in the 1990s by the national Forest Management Act (Gilmour 2003).
Community forestry programs give local users some degree of autonomous resource management, and include the forest ecosystem and the group of people that actively contribute to the management of the forest resources. Globally, they have encountered differing levels of success (Charnley & Poe 2007). Some are entirely managed by local organizations, while others are formally owned by the national, state, or regional governments with management rights held by locally established community forest management committees (White & Martin 2002). The complex human-environment dynamics and the heterogeneity in management and decision processes in community forestry situations make them an excellent candidate for agent-based modeling (Janssen & Ostrom 2006).
Chitwan community forest user groups have faced a variety of challenges, such as increasing urbanization, but more recently a rapidly growing invasive plant (Mikania micrantha, referred to as Mikania) has disturbed the system. Mikania is a vine-like plant that is difficult to successfully remove partially due to its sexual and asexual reproduction. If not properly contained after removal efforts during the flowering season, the seeds can further spread the plant (Barreto & Evans 1995) and pieces of dropped stem can result in unintended regrowth (Murphy et al. 2013). Mikania grows on the forest floor and climbs small trees, meaning it is often tangled in fodder and grasses that community forest users collect. Thus, commonplace resource collection and management efforts have resulted in aiding Mikania dispersal (Sullivan et al. 2017a).
To manage Mikania, people in Chitwan engage in a variety of removal strategies and/or follow management norms. These include doing nothing; mechanical removal (pulling/uprooting and cutting/slashing the plant); burning; use of herbicides; pulling the plant and burying it in a deep hole; and a best practice method that involves uprooting, bagging, burying, and burning the plant. These practices are considered strategies in terms of the institutional grammar (AIC), as they include attributes (e.g. households that are members of a community forest), an aim (e.g. to remove Mikania by pulling), and conditions (such as the time of year removal will be performed). These strategies can sometimes also be classified as norms (ADIC), as deontic elements are occasionally present. For example, households may be forbidden (must not) to use herbicides in some areas of their community forest, subject to their community’s rules, and typically at least one member of each household should participate in removal efforts. Additionally, there is a norm associated with burning, as burning in the forest is forbidden or permitted according to a given community forest’s rules (in most cases burning is forbidden). This burning norm does not become a rule in most cases, as there are not consistent sanctions (or else) associated with the practice.
How do institutions change?
There are several theories of institutional change (Table 1). These theories are at times competing, but often elements of separate theories are compatible. Here, we describe two main categories of institutional change, while acknowledging there are others.
| Type | Description | Examples | Problems | Citations |
| Centralized | Deliberate/purposeful; not usually accidental (but can have unintended consequences); often occurs via a political process or collective choice mechanism | Origin of property rights via ‘contracting’; Cost-benefit analysis embedded in Ostrom’s constitutional- collective choice- operational rule hierarchy | Difficulty explaining when/why ‘formal’ rules are ineffective/ignored and addressing “informal” institutions, such as social norms | Libecap (1994), Ostrom (2005), Alston (1996), Kantor (1998) |
| Decentralized | Described as evolutionary (where institutions emerge via a decentralized selection process), incremental; new institutions can emerge at random and sometimes through design | Transaction cost literature where most efficient institutions are assumed to survive; habits that cause emergent actions; punctuated equilibrium | Often neglects roles of collective action/political processes in institutional change | Williamson (2000), Veblen (1999), Hayek (1978), Young (1996) |
The primary distinction we draw between theories of institutional change is deliberate change that occurs via a centralized mechanism (like collective-choice situations) versus evolutionary change that occurs via a decentralized mechanism (Kingston & Caballero 2009). Institutional change that occurs in a deliberate manner in a centralized process (such as through legislation) tends to occur more quickly than institutional changes that occur via a decentralized process. It has been noted that ‘formal’ institutions, often defined as written rules (such as laws) and rules using the institutional grammar tool, are more frequently changed deliberately, whereas ‘informal’ institutions (strategies and norms using the institutional grammar tool) are slower to change and shift in a decentralized process resulting from uncoordinated micro-level behaviors.
Informal institutions include unwritten agreements, moral or ethical norms, and social norms. Institutional change may also occur, via both centralized and decentralized processes, in a punctuated manner with periods of stability interrupted by points of rapid transition. Understanding rates of institutional change is important to policy makers and stakeholders attempting to deliberately change either formal or informal institutions (Mahoney & Thelen 2010). The two perspectives in our model, rational choice and cultural diffusion, explore decentralized processes of institutional change, with individuals interacting on the micro-level potentially leading to changes in the composition of strategies and norms on the macro-level over time.
Rational choice is explored in the first sub-model. Considering the rational choice perspective, under a bounded rationality framework, individuals seek to maximize their own utility under cognitive, information, and time constraints (Bohensky 2014; Ostrom 2005). In this case, agents engage in a cost-benefit analysis; if the perceived value of adopting a specific strategy is greater than its cost, the agent can select a management method costlier than the least costly method. Although the cost-benefit analysis in the model occurs at the micro-level, the process is similar to Ostrom’s theory of institutional change where individuals engage in a cost-benefit analysis and agree to institutional change if a ‘minimum coalition’ is achieved (Ostrom 2005, p.61). Instead of the change taking place on the scale of the entire community simultaneously (i.e. individuals are not voting or agreeing on a threshold where everyone will adopt one institution after the 'minimum coalition' is met, such as a majority in democratic voting processes), the change takes place as individuals adopt specific strategies over time.
Our second perspective of change investigated is cultural diffusion, based on Axelrod (1997). Axelrod explored how simple interactions between agents with some level of cultural similarity stimulated changes in cultural heterogeneity over time. We modify the model to examine institutional change by modeling Mikania management strategies and norms and tracking the changes in these and Mikania patterns over time. They change via individual agent interactions and the mechanism of change can be thought of as social learning (Caldas & Coelho 1999).
Human decision making under assumptions of bounded rationality has been supported in some experimental studies, but these studies have also been criticized for bias, particularly regarding the narrow type of participants that have been included in the research (e.g. college educated, western, rich; Henrich et al. 2010). The model of cultural dissemination or diffusion has not been empirically validated, a common issue with many computational social science models (Railsback & Grimm 2011). However, Stivala et al. 2014 employed an empirical dataset related to public opinions to analyze the importance of spatial configurations in the results of the Axelrod model and discovered that the level of cultural diversity varied depending on spatial configurations. It is difficult to observe institutional change and there remains opportunity for computational models validated with empirical data to contribute to understanding institutional change and provide new directions for future empirical research.
Conceptual Model
This model is informed by ethnographic fieldwork and survey data collected in 2014 and 2015 in Chitwan, Nepal. The ethnographic fieldwork included semi-structured interviews with 87 individuals focusing on governance relationships in community forestry and Mikania in five community forests, while the survey included 1041 households in 21 community forests. All community forests in the fieldwork and survey are located around the border of Chitwan National Park in the area known as the buffer zone. The fieldwork and survey include data on Mikania management strategies and norms in communities and the specific strategies and norms employed by each household (Table 2). The ethnographic data are used to inform the removal cost parameters, while the survey data are compared to the model results to explore which perspective of institutional change best fits the data. The agents in this model represent households distributed on a virtual landscape. The model code is available at: https://www.openabm.org/model/5231/version/1/view.
| Strategies and norms | Characterization of time intensiveness (from ethnographic data, informs cost parameters) | Percent using method (from survey data, used for model validation) |
| Burning | Low cost | 17 |
| Mechanical removal | Medium cost | 34 |
| Pulling and burying | High cost | 7 |
| Best practice | Highest cost | 0 |
We provide an overview of the model setup and processes, including a summary of input and output variables in Table 4 in the Appendix, which follows the Overview, Design concepts, and Details (ODD) protocol (An et al. 2014; Grimm et al., 2006, 2010). We implemented our model using NetLogo (version 5.3.1) (Wilensky 1999).
Set up
The model includes two elements: the landscape and the agents. The agents represent households that make individual decisions regarding Mikania management. The model can be initialized with 100 to 1000 agents; all simulations analyzed here were initialized with 100 agents because this represents an average neighborhood size. The agents are aware of their geographic location (in NetLogo, their patch ID), their own features, and the environment (Mikania cover and land productivity). Agents are randomly placed on a landscape composed of individual spaces, called patches in NetLogo, and each patch represents one plot within a forest. The landscape is set up with a gradient of Mikania cover, with patches ranging from 0 to 75 percent initial cover (see Appendix).
Model sequence
After initializing model parameters, the model enters procedures to ‘remove Mikania’ and ‘redistribute Mikania.’ In order to manage Mikania (the ‘remove Mikania’ procedure), agents enter the rational choice or cultural diffusion sub-models, depending on which sub-model the model analyst has selected (the cultural diffusion and rational choice sub-models are independently processed). The ‘redistribute Mikania’ procedure impacts Mikania distribution depending on the removal method an agent used in that time step (i.e. Mikania in a given patch may change) based on a rate of increase. See pseudo code below.
Managing Mikania
Rational choice
In the ‘rational choice’ sub-model (Figure 1), an agent enters a cost-benefit analysis and observes their neighbors to adopt a Mikania management strategy (see pseudo code below). The cost (in in terms of time and personal effort) associated with each strategy is ranked based on the ethnographic fieldwork, essentially an ordinal variable. The ordering is accurate, but the distance between the numbers is unknown (i.e. how much costlier it is to conduct mechanical removal versus burning). Because of this, we systematically varied the value of each cost parameter to understand the impact of different costs for each strategy, while maintaining the ranking of the costs (Yang and Gilbert 2008). The analysis showed that as long as the ranking is not altered (i.e., not sensitive to the distance between different strategies), the pattern in adoption of strategies holds. The agent’s preferences and their observation (and possible imitation) of their neighbors’ strategies drives change. In absence of empirical data on management preferences, they are modeled as a random value between 0 and 1. In reality, this value could be influenced by income, reliance on forest resources, household size, and other factors. Similar factors have been modeled this way (Broekhuizen et al. 2011; Zhang & Vorobeychik 2016) and we subject this parameter to sensitivity analysis (for example, to understand what happens when more than half of agents have a value above 0.5, representing a strong preference to remove Mikania). This assumption is a limitation of the model, but the parameter can be recalibrated in the future with empirical survey data to explore the impact on the results, similar to the methods employed by Parker et al. (2012).

Cultural diffusion
The cultural diffusion sub-model is a modification of the “Diffusion of Culture” model from openABM (Lozano & Maes 2008), based on Axelrod’s (1997) article. It operates on the premise that agents interact with culturally similar agents, and have the possibility to imitate the Mikania management practices of culturally similar agents (Figure 2). The agents are initialized with high levels of mechanical burning (40 percent) and low levels of burning (10 percent) and best practice removal (5 percent), informed by the removal patterns in Chitwan from the ethnographic fieldwork. This percentage of agents initially adopting different strategies is varied in 16 different experimental scenarios later on. Agents each have a set of cultural traits represented as a randomly assigned string of length n (n ranges from 1 to 20 traits). Each of these traits has m possible features (m can range from 1 to 20). The first trait in the string represents the Mikania management strategy that an agent adopts, with five possible features (for the first trait, m = 5: doing nothing, mechanical removal, pulling and burying, burning, best practice). Agents evaluate whether to interact or not with the spatially closest agent based on the similarity of their features. If agents are similar, it is possible they will interact. If they interact, the active agent may adopt a feature of the other agent, increasing their similarity. Here again, if an agent engages in removal, they remove Mikania from their current location.

Redistributing Mikania
Each Mikania removal strategy is tracked within the model based on the cost of an agent’s current strategy (rational choice) or the value of the feature of an agent’s first trait (cultural diffusion). Each removal strategy corresponds to a parameter that influences how likely Mikania will increase and possibly spread into a neighboring patch, which was determined by discussing the different strategies with experts and was subject to a sensitivity analysis where the redistribution parameter for each strategy was varied between 0 and 1, in increments of 0.1, while holding other parameters constant. The analysis showed little variation in the overall model outcomes (e.g. the higher the removal parameters, the more Mikania increased).
Cultural diffusion scenarios
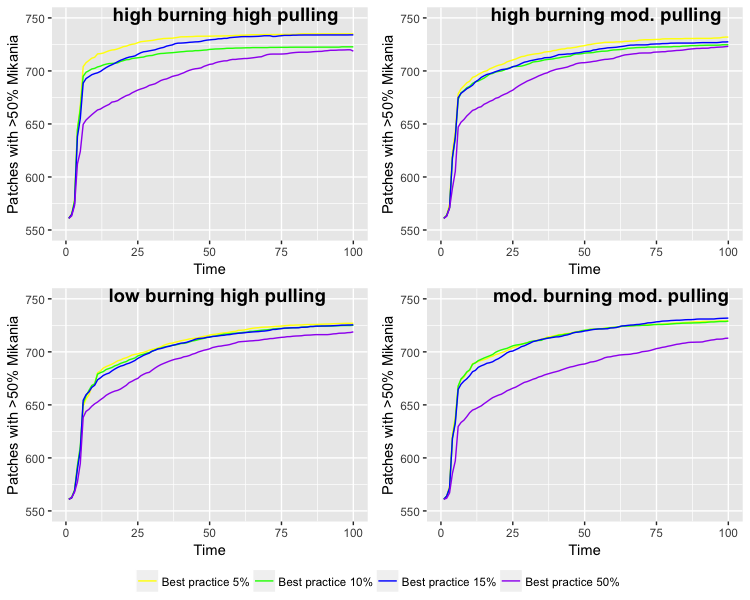
We additionally assess experimental scenarios to explore the impact of different percentages of agents adopting the best practice removal method in the cultural diffusion sub-model (Table 3). These scenarios are designed to test the hypothesis that higher initial percentages of agents adopting the best practice removal method will reduce Mikania, even with burning still occurring. We selected scenarios varying the initial percentage of agents adopting the best practice removal method from 5 to 50 percent informed by the ethnographic fieldwork. There are four scenarios with high, low, or moderate burning. Scenario C follows the observed management patterns (high mechanical removal, low burning). Scenarios A, B, and C are respectively high, moderate, and low burning paired with high levels of mechanical removal. Scenario D pairs moderate levels of burning with moderate levels of mechanical removal. In each scenario, we vary the percentage of agents initially adopting the best practice removal strategy from 5 to 50 percent, which represents part of our sensitivity analysis (ten Broeke et al. 2016).
| Initial best practice | Initial burning | Initial pulling | |
| (A)High burning, high mechanical removal | 0.05 0.1 | 0.4 0.4 | 0.4 0.4 |
| 0.3 0.5 | 0.35 0.25 | 0.435 0.25 | |
| (B) Moderate burning, high mechanical removal | 0.05 0.1 | 0.25 0.25 | 0.4 0.4 |
| 0.3 0.5 | 0.25 0.25 | 0.4 0.4 | |
| (C) Low burning, high mechanical removal | 0.05 0.1 | 0.1 0.1 | 0.4 0.4 |
| 0.3 0.5 | 0.1 0.1 | 0.4 0.4 | |
| (D) Moderate burning, moderate mechanical removal | 0.05 0.1 | 0.25 0.25 | 0.3 0.3 |
| 0.3 0.5 | 0.25 0.25 | 0.3 0.3 |
Results
The results are the averages of 30 model runs. Due to the agents’ fixed spatial configurations, the model parameters stabilized around 100 time steps; thus, each model was stopped after 100 time steps. In both the rational choice and cultural diffusion cases, Mikania gradually decreases over time, but Mikania decreases slightly more with cultural diffusion. In the rational choice case, most agents select the least costly management strategy (burning) even with observation of their neighbors’ strategies (Figure 3, top). In the cultural diffusion case, few agents (10 percent) begin with the best practice management strategy, and this amount is reduced as agents interact and adopt other common strategies (Figure 3, bottom).

In the cultural diffusion scenarios, we explore the change in management strategies over time when the percentage of agents initialized with the best practice strategy is altered (see cultural diffusion scenarios in the methods section). In the first analysis, the scenarios outlined in Table 3 were run with the initial amount of Mikania removed (by an agent participating in removal) set to less than 20 percent (Figure 4). Second, the scenarios were run with initial amount of Mikania removed set to greater than or equal to 20 percent (Figure 5). The results revealed a tipping point around 20 percent. With the initial amount removed varied between 0 and 19 percent, Mikania gradually increases over time, while with the initial amount removed varied between 20 and 70 percent, it gradually decreases over time. Regardless of the amount of Mikania initially removed, increasing the percentage of agents adopting the best practice method resulted in Mikania either increasing the least or decreasing the most.

Discussion
The primary objective of the model analysis was to assess which theoretical perspective of institutional change best fits empirical data on efforts to manage the invasive plant Mikania micrantha. The rational choice perspective explored institutional change subject to agents seeking to reduce their costs, while also considering what their neighbors were doing (Figure 3, top). The cultural diffusion perspective examined how institutions gradually shifted over time in response to interactions with other culturally similar agents (Figure 3, bottom; Figures 4 and 5). The model results from these perspectives are largely intuitive based on common pool resource, cooperation, and economics literature but the computational approach allowed us to alter and analyze features of these perspectives such as observation and the initial amount of Mikania removed. We found somewhat counterintuitively that the initial percentage of agents adopting the best practice Mikania removal method was not as important in reducing Mikania spread as the initial amount of Mikania removed (i.e. using any removal strategy was more effective if greater than 20 percent of the Mikania was removed). These results imply that it may be beneficial to conduct a study empirically assessing the impact of the initial amount of Mikania removed on the success of management efforts (i.e. amount of Mikania present a specified time after removal). This seems especially relevant to understand because the best practice strategy for Mikania removal is also the most time consuming strategy. If the success of less time consuming strategies could be increased by initially removing more Mikania, this would be useful information for community forest members in Chitwan allocating their limited time and hoping to maximize the success of their management efforts.
Many of the results from the rational choice case are intuitive from previous research. In particular, the finding that the majority of agents select the least costly common pool resource management strategy (burning Mikania) is consistent with utility-maximizing agents (Figure 3, top). In the cultural diffusion sub-model, the initial percent of agents adopting a given management strategy influenced the change in strategies, via meetings between culturally similar agents. There was variation in agents adopting different types of strategies, as opposed to primarily burning (Figure 3 bottom, 4, 5).
Validation: which perspective better fits empirical data?
To understand which of our theoretical perspectives, rational choice or cultural diffusion, most closely represents data on Mikania management in Chitwan, we compare model results to surveys of households near Chitwan National Park. Fieldwork and an understanding of on-the-ground conditions can be an important indicator of model validity (Ghorbani et al. 2015; Yang & Gilbert 2008).
In the rational choice perspective, most of the agents adopt the least costly strategy (burning). This was not the case in survey data from Chitwan, where only 17 percent of households reported burning Mikania. Based on interviews, discussing burning can be a sensitive subject as some community forests have rules against burning or restrictions on when burning can be conducted. Thus, the actual number of households engaging in burning is possibly higher than that reported in the household survey, but it is unlikely the percentage of agents engaging in burning reaches the levels in the rational choice sub-model. Consistent with empirical and experimental literature on rational choice and natural resources (Ostrom 2005), it is unlikely that the rational choice sub-model captures how institutional change occurs in Chitwan community forests. People reported engaging in collective action to remove Mikania based on their neighbors’ decisions or informal social norms that required at least one person from a household to participate. This decision making process is similar to the learning and imitation that is the primary mechanism of change in the cultural diffusion sub-model (as opposed to only partially influencing change, like observation in the rational choice case). Many humans do not conform to the rational actor model (e.g. Richerson & Henrich 2012’s review) and humanity’s ability to socially learn and imitate is likely what has allowed humans to thrive in changing environmental conditions (Mathew & Perreault 2015). Our survey data are most consistent with the results of the cultural diffusion scenario C, where only 10 percent of agents end with the burning strategy and 3 percent with the best practice method (from the survey, 17 percent burn and no one had yet adopted the best practice method). The observation that the results from the cultural diffusion sub-model better fit empirical data on Mikania management indicate that it is a possible mechanism of institutional change in Chitwan, but the results of this model cannot confirm that cultural diffusion is the actual or only way institutions will change over time. The challenges of empirically validating model parameters, like those influencing how Mikania spreads, means that our model results should be interpreted with caution, with a focus on the general patterns observed and possibilities identified for future empirical data collection and validation. Next steps include collecting additional data to empirically validate model parameters and comparison of cultural diffusion with other theories of institutional change.
Institutional fit and future directions
In cases where there are historical institutions that exacerbate a newer social-ecological disturbance, implementing best practices for common pool resource management, like monitoring and sanctioning, may not be effective. In Chitwan, the norm of burning for other reasons (i.e. traditional agricultural or forest management practices) is long standing (Nagendra 2009), but unintentionally aids in Mikania dispersal (Murphy et al. 2013). Because of the relative ease of burning in terms of labor/time compared to other management options, some agents still opt for this strategy even with sanctioning, which contributes to Mikania’s continued spread. The case of fit between existing institutions and current social-ecological challenges has been previously addressed (Dietz et al. 2003; Folke et al. 2007; Young 2002), with the conclusion that institutions need to change and evolve to support sustainable governance of the commons. Where existing institutions and new social-ecological challenges conflict, the introduction of outside information may be useful in supporting such governance and change.
In the case of Chitwan and Mikania, people engage in burning both because it is a less costly strategy, but also because they believe it will have some level of success in removing Mikania. Mikania is a relatively new disruption and issues of trust between actors in Chitwan can limit information sharing, resulting in many households and community members lacking access to information on effective removal (Sullivan et al. 2017b). As new disturbances appear as global climate and social structures continue to change, natural and common pool resource management situations may benefit from increased access to new knowledge coupled with implementing best practices. The introduction of new information to communities that are managing their own natural resources, particularly indigenous communities, may not always be welcome due to past experiences with colonialism, paternalistic knowledge imposition, and the disrespect of local ecological knowledge (Gratani et al. 2011; Mazzocchi 2006; Nightingale 2005). Thus, the information provider, an outsider versus a community member, is important (Nightingale 2005). It is also important that the community desires outside information or assistance with assuaging a disturbance or information provided is unlikely to be embraced or implemented. When exogenous institutions are imposed, they may crowd out a community's intrinsic environmental motivation to manage a resource sustainably. In contrast, when endogenous, participatory management norms (established at least partially by community members) are in place, intrinsic environmental motivation can facilitate successful natural resource management (Vallino 2014). This is important to consider in the context of Chitwan when introducing a new management method or other information, including suggestions informed by modeling such as to conduct empirical experiments on initial amount of Mikania removed.
Institutions can also change via migration processes, which can introduce new institutions, or shift the composition of existing ones. Migration is an integral part of the history of the Chitwan Valley, with new migrants regularly entering and others emigrating to nearby countries to work and send remittances to family members (Bohra & Massey 2009; Massey et al. 2010). The introduction of new institutions via migration is a process that could be explicitly modeled in future efforts. The model could also be extended to include local specifics (like geographic information systems data, social networks, etc.) to attempt to explicitly predict Mikania distribution in Chitwan or elsewhere. Further, agent-based models have also been designed in a process known as companion or participatory modeling where stakeholders are actively involved in structuring the model from the start to increase its structural validity and community relevance (Moss 2008), which is another potential avenue.
Conclusion
In this research, we assessed an agent-based model to explore how two different perspectives of institutional change fit empirical data in a social-ecological system facing rapid change. Agent-based models can serve as virtual laboratories that simultaneously allow researchers to explore generalizable properties and local implications (Magliocca et al. 2015). In this sense, they can further the study of different theories of institutional change important to natural resource management that would otherwise be challenging to observe and assess. We used survey data to understand the validity of the two perspectives and concluded that (1) it is unlikely the rational choice perspective represents how institutions change in Chitwan over time and (2) it is possible institutional change in Chitwan follows the cultural diffusion perspective, underscoring the importance of social learning in communities faced with variable environmental conditions (Mathew & Perreault 2015). The latter is an important area for further study, especially comparing cultural diffusion to other perspectives of institutional change and analyzing institutional change in other social-ecological systems.
Acknowledgements
This research was supported in part by National Science Foundation grants CNH-1211498 and SES-1462086. We thank two anonymous reviewers for their helpful feedback.Appendix: Model Details and ODD Protocol
Overview
In this appendix, we follow the ODD protocol (Grimm et al. 2010), with a few modifications and additions for coupled human and natural systems (CHANS) based on An et al. (2014), to present details of the agent-based model in the accompanying manuscript.
Purpose
The model is intended to explore how institutions for invasive species management change over time. Two perspectives of institutional change are examined, rational choice and cultural diffusion. The model is informed by data from locally governed community forests in Chitwan, Nepal and seeks to understand how management strategies influence the spread of a rapidly growing invasive plant, Mikania micrantha. The primary purpose of this model is to explore which theoretical perspective of institutional change best fits empirical data from Chitwan.
Entities, state variables, and scales
The model is constructed in NetLogo, where spaces are represented as “patches.” Agents are randomly placed on a landscape composed of individual spaces, called patches in NetLogo, and each patch represents one plot within a forest. The landscape is represented by a two-dimensional grid, consisting of 1024 patches. Patch, agent, and global variables are in Table 4.
Agents in the model represent households and the model can be initialized with 100 to 1000 households, which are randomly distributed on the landscape; the baseline is 100 households. Each patch represents an area of community forest land. The patch can either be highly productive to an agent, or completely degraded. Each patch is invaded by a percentage of Mikania, which varies depending on the set up (gradient distribution versus random distribution; see Table 4). The ranking/ordering of some of the parameters was determined from ethnographic fieldwork conducted in Chitwan in 2014. The model runs indefinitely (no stopping condition), but all simulations were stopped after 100 time steps because outcomes stabilized at this point.
| Variable | Features | Explanation |
| Agent_removed | Initialized to 0 for every agent | Changes to 1 if agent removes Mikania |
| Num_HH | 100-1000 in increments of 50 | The number of agents in the model |
| Mikania_cover | Patch variable; initialized between 0 and 1 | A value of zero corresponds to zero percent Mikania, a value of 1 corresponds to 100 percent of the patch being covered with Mikania |
| Redistribute_Mikania | 0-1 in increments of 0.5; Default is 0.1 for pulling/burying, 0.2 for pulling; 0.3 for burning | The higher the parameter, the more likely Mikania will spread; default parameter values were ranked based on discussion with experts; the range allows for sensitivity analysis |
| Only used in cultural diffusion sub-model | ||
| Number_of_regions | Initial value varies depending on number of features and traits selected | An outcome variable; the number of distinct cultural regions currently in the model |
| Regions_list | A list of identifiers for each region | |
| Closest-person | Equals the closest agent to the current agent based on agents’ x and y coordinates | Used to determine who the agent will evaluate if they interact |
| Feature_nb | After two agents have interacted, this is used to copy the value of one of the agent’s features to the active agent | |
| Overlap | The overlap between two agents, i.e. their similarity. This determines whether the agents will interact and adopt traits | |
| Chosen-feature | The feature that will be adopted by the active agent | |
| New-trait | The feature adopted from the active agent’s neighbor | |
| Feature | Initialized as a string of length N (N = 1 to 20; number of traits) | Abstract numerical list of the cultural features (including shared strategies and norms) of each agent |
| Region_id | The region an agent belongs to | |
| Institution_type | Equals 0, 1, 2, 3, or 4, corresponding to the first item in the feature list | Used to track the management strategy the agent has adopted |
| Featval0 | Equals the value of the first item in an agent’s feature list (0, 1, 2, 3, or 4) | Used to model the 5 different Mikania management norms and the change in their composition over time |
| Number_of_traits | Ranges from 1 to 20 | |
| Number_of_Features | Ranges from 1 to 20 | |
| Mutation_rate | Ranges from 0 to 0.1 in increments of 0.0005 | The rate of mutation, via random change in features. Set to zero for all model analyses; an area for future exploration |
| Random_interaction | Ranges from 0 to 100 percent | Set to zero for all model analyses; an area for future exploration |
| Only used in rational choice sub-model | ||
| Productivity_value | Patch variable; randomly initialized between 0 and 1 | A value of 0 indicates the patch is completely degraded/not useful to the agent; the lower the value, the less likely an agent will remove Mikania from the patch |
| Value_threshold | Each agent is randomly assigned a value between 0 and 1 | Used in the cost-benefit analysis; if the value is greater than 0.5, the agent selects a method other than the least costly method |
| Removal_cost | Initialized at zero, changes as agents make management decisions | Keeps track of the current management strategy an agent has adopted |
| Removal_list | List containing the possible Mikania removal costs (0.2, 0.3, 0.35, 0.5) | Each removal strategy corresponds to a cost |
| Three_removal_list | List containing the Mikania removal costs, less burning | Used when excessive burning fee is implemented (can only be implemented when “monitor_and_sanction_burning?” is turned on); agent selects alternative removal method if engaging in removal |
| Times_burned | 0 when simulation begins; updated after agent burns | Count of times agent has burned; used when “monitor_and_sanction_burning?” is turned on |
| Num_bp | Ranges from 0 to 1 | Slider in NetLogo; used to set the initial percentage of agents employing the best practice strategy |
| Num_nothing | Ranges from 0 to 1 | Slider in NetLogo; used to set the initial percentage of agents not engaging in removal |
| Num_pull | Ranges from 0 to 1 | Slider in NetLogo; used to set the initial percentage of agents employing the mechanical removal strategy |
| Num_pull_bury | Ranges from 0 to 1 | Slider in NetLogo; used to set the initial percentage of agents employing the pulling and burying strategy |
| Num_burn | Ranges from 0 to 1 | Slider in NetLogo; used to set the initial percentage of agents employing burning |
| Monitor_and_sanction_burning? | True, False | Button in NetLogo. Turns on/off the monitor and sanction burning procedure |
| Observe? | True, False | Button in NetLogo. Turns on/off the observe procedure |
Process overview and scheduling
In each time step, an agent makes decisions about which Mikania management strategy to adopt (including doing nothing). An agent will either enter the rational choice or cultural diffusion sub-model to make this decision depending on which is turned “on” in NetLogo (the sub-models can be controlled using a “button” in NetLogo). The agents only enter one of the decision making sub-models at a time. After making management decisions, the next procedure updates the amount of Mikania in each patch based on the agents’ selected strategies.
Set up
The landscape is represented by a two dimensional grid, consisting of 1024 patches. Each patch has a randomly assigned corresponding ‘productivity value’ ranging from 0 to 1, where 0 represents highly degraded land or land that is otherwise useless to an agent. Each patch additionally has an initial ‘Mikania cover’ value, ranging from 0 to 1, that represents the percent of the patch that is populated with Mikania. The landscape can be setup with a gradient of Mikania cover, with groups of patches initially ranging from 0 to 75 percent cover (0 to 0.75), or with a random distribution of Mikania cover, with each patch randomly assigned a cover value. Conversations with ecological experts working with Mikania data in Chitwan indicated that a gradient of cover more accurately reflects the actual distribution, so it is used as the basis for all analyses presented and discussed.
Remove Mikania
Rational choice
The cost (in terms of time and personal effort) associated with each strategy is ranked based on the ethnographic fieldwork, essentially an ordinal variable. The ordering is consistent with empirical observations, but the distance between the numbers is unknown (i.e. how much costlier it is to conduct mechanical removal versus burning). Because of this, we conducted a sensitivity analysis to explore the impact of different costs for each strategy, while maintaining the ranking of the costs. See Yang and Gilbert (2008) for a conversation on parametrizing qualitative data.
Cultural diffusion
The “Diffusion of Culture” model that this sub-model is based on investigates a variety of variables that influence how quickly culture homogenizes over time, including a rate of mutation and the inclusion of random interactions. In this modification, we focus on tracking the impact of the initial percentage of agents with each Mikania management strategy and do not analyze these additional variables.
Redistributing the Mikania
The values for the rate of increase for each strategy were selected based on a combination of literature and expert opinion. The values for the rate of increase were also systematically varied in the model to explore the impact of different rates and can be adjusted as new information is available. When the Mikania cover of a patch is greater than 0.5, the Mikania from that patch spreads to a neighboring patch.Design concepts
Basic elements
The model draws on theory from common pool resource and collective action literature, as well as literature on cultural dissemination, cooperation, and social learning (An 2012; Axelrod 1997; Mathew & Perreault 2015; Ostrom 1990). Changes in institutions (shared strategies and norms for Mikania management) influence the amount of Mikania in a given patch, which influences the cost of the agent’s actions and future management decisions/institutional change.
Adaptation
In the cultural diffusion sub-model, agents can adopt another agent’s Mikania removal strategy if their list of cultural traits are similar. Other adaptation could be possible in future models, but is not currently present. For instance, agents can change their behaviors (their selected removal strategy) in response to others and the environment, but the parameters that determine these behaviors are currently fixed. For instance, an agent’s “value threshold” in the rational choice sub-model does not change over time.
Observation
Data are collected for testing and observation using the BehaviorSpace extension in NetLogo (see https://ccl.northwestern.edu/netlogo/docs/behaviorspace.html and https://www.openabm.org/book/3138/how-use-behavior-space). We observe two primary outcomes: the change in Mikania over time and the change in composition of management strategies over time. The model allows for additional observation of other factors including the impact of a mutation rate and random interactions in the cultural diffusion case. However, these are not explored in this analysis of the model.
Emergence
Changes in the composition of Mikania removal strategies and amount of Mikania emerge over time based on low-level agent interactions and decisions. The agents’ interactions and decisions are governed by the sub-model components, either rational choice or cultural diffusion.
Objectives
The objective of the agents depends on the sub-model. In the rational choice case, an agent’s goal is to maximize their utility subject to a set of preferences. In the cultural diffusion sub-model, agents do not seek to maximize an objective; they may adopt other similar agent’s strategies and norms on the basis of interactions.
Prediction
Agents do not use prediction in their decisions.
Learning
One feature in the rational choice sub-model is “observation.” Agents observe their closest eight neighbors when the “observe” feature is turned on and may change their behavior to the most common behavior. In the cultural diffusion sub-model, the implicit mechanism of exchange of norms and strategies between similar, interacting agents is social learning or imitation.
Sensing
Each agent knows their own set of preferences in the rational choice sub-model. Each agent is assumed to know the productivity of each patch. These each inform agent decisions in the model. The agents do not know the total amount of Mikania in the world (global information).
Interaction
In the rational choice sub-model, agents check the behavior of other agents if the observe feature is on. In the cultural-diffusion sub-model, an agent has the opportunity to interact with the closest agent at each time step. If they are similar enough, they will possibly exchange cultural information.
Collectives
There are no collectives in the model.
Initialization
See Table 4 for the values agents and patches are initialized with.
Input data
No input data is used in this model.
Submodels
Both the rational choice and cultural diffusion sub-models are theoretically driven. The parameters for the cost of each of the management strategies in the rational choice sub-model were ranked based on ethnographic fieldwork. The model code is available at https://www.openabm.org/model/5231/version/1/view.
CHANS characteristic features
Human-environment systems have been known to exhibit features such as time lags, resilience, heterogeneity, and feedback loops (An et al. 2014). This model exhibits resilience to Mikania reduction beyond specific thresholds (once Mikania takes over the world, it is very difficult to remove or control). There is heterogeneity in the management strategies adopted over time. One of the feedbacks observed in the rational choice sub-model includes the relationship between the selected strategy, Mikania redistribution, and subsequent impacts on agents’ strategy selection. For example, an agent may select burning as their removal strategy; burning is associated with the highest rate of Mikania increase in the agent’s current patch after removal. If an agent continues to select burning as their removal method due to its low cost, the amount of Mikania in the patch will continue to increase and there will be an additional removal cost to the agent in patches with a density greater than 0.5; if the cost of removal becomes greater than the productivity of the patch the agent may decide to stop removing Mikania (a “do nothing” strategy).
Verification and validation
Model validation is discussed in the accompanying manuscript, with a general discussion here. Following advice from Railsback and Grimm (2011) and An et al. (2005), model validation included checks for structural validity, including conversations with experts, and a comparison of empirical fieldwork and model output. Verification was an iterative process that included a continuous debugging of the model as it was coded, running extreme value tests (where model responses when parameters were set to extreme values were assessed), and sensitivity analyses (assessing how the model responded to small parameter changes). The results of the extreme value tests and sensitivity analysis are largely consistent with our qualitative data and field observations.
The model parameters are primarily informed by previous literature and empirical observations from ethnographic fieldwork conducted in Chitwan in 2014. Although most agent-based models are validated using quantitative data, there has been a growing conversation about the importance of incorporating qualitative data into the model creation and validation processes and several authors have assessed agent-based models informed by ethnographic data (Dean et al. 2000; Agar 2005; Huigen et al. 2006; Yang and Gilbert 2008).
Simulation experiments and sensitivity analysis
Below are results from sensitivity analyses and extreme value tests.
| Parameters | Default value | Min, Max | Mikania cover: min, max |
| Initial-people | 100 | 100, 1000 | 542.3, 1080.7 |
| Monitor_and_sanction_burning? | False | False, True | 542.4, 528.5 |
| Observe? | False | False, True | 542.3, 541.4 |
At t=100, average of 30 runs.
| Parameters | Default value | Min, Max | Mikania cover: min, max |
| Initial-people | 100 | 100, 1000 | 524.2, 1061.3 |
| Num_bp | 0 | 0, 1 | 507.8, 524.3 |
| num_burn | 0.15 | 0, 1 | 527.2, 538.1 |
| Number_of_Features | 5 | 1, 20 | 546.2, 529.3 |
At t=100, average of 30 runs.
To calculate the sensitivity \(S_x\), below, the following formula was used (An et al. 2005; ten Broeke et al. 2016):
\(S_x = \frac{(\frac{\Delta D}{D})}{(\frac{\Delta )}{I})}\) where I is the value of the independent variable, \(\Delta I\) is the change in \(I\), \(D\) is the value of the dependent variable, and
\(S_x = \frac{(\frac{\Delta D}{D})}{(\frac{\Delta )}{I})}\) where I is the value of the independent variable, \(\Delta D\) is the change in \(D\) in response to the change in \(I\).
| Variable | Default value | Perturbation + 50% | Change in Mikania cover (number of patches with >50% cover) | Sensitivity |
| Initial-people | 100 | 150 | 4.6 | 0.006 |
| Initial-mikania | 0.3 | 0.45 | 2.8 | 0.004 |
At t=100, average of 30 runs.
| Variable | Default value | Perturbation + 50% | Change in Mikania cover (number of patches with >50% cover) | Sensitivity |
| Initial-people | 100 | 150 | 1.1 | 0.001 |
| Initial-mikania | 0.3 | 0.45 | 1.8 | 0.002 |
| Num_bp | 0 | 0.05 | 0.1 | 0.0001 |
| num_burn | 0.15 | 0.25 | 2.3 | 0.003 |
| Number_of_Features | 5 | 8 | 5.9 | 0.007 |
At t=100, average of 30 runs.
References
AGAR, M. (2005). Agents in living color: Towards emic agent-based models. Journal of Artificial Societies and Social Simulation, 8(1), 4: https://www.jasss.org/8/1/4.html.
ALSTON, L. (1996). 'Empirical Work in Institutional Economics: An Overview'. In L. Alston, T. Eggertsson, & D. North (Eds.), Empirical Studies in Institutional Change (pp. 25–30). Cambridge: Cambridge University Press. [doi:10.1017/CBO9781139174633.004 ]
AN, L. Linderman, M., Qi, J., Shortridge, A., & Liu, J. (2005). Exploring complexity in a human-environment system: An agent-based spatial model for multidisciplinary and multiscale integration. Annals of the Association of American Geographers, 95(1), 54-79. [doi:10.1111/j.1467-8306.2005.00450.x]
AN, L. (2012). Modeling human decisions in coupled human and natural systems: Review of agent-based models. Ecological Modelling, 229, 25–36.
AN, L., Zvoleff, A., Liu, J., & Axinn, W. (2014). Agent-Based Modeling in Coupled Human and Natural Systems (CHANS): Lessons from a Comparative Analysis. Annals of the Association of American Geographers, 104(4), 723–745. [doi:10.1080/00045608.2014.910085]
ATLAN, A., & Darrot, C. (2012). Invasive species between biology and social sciences: what distinctive features for French overseas territories?. Revue d'Écologie, Terre et Vie, 101-111.
AXELROD, R. (1997). The Dissemination of Culture A Model with Local Convergence and Global Polarization. Journal of Conflict Resolution, 41(2), 203–226. [doi:10.1177/0022002797041002001]
BARRETO, R. W., & Evans, H. C. (1995). The mycobiota of the weed Mikania Micrantha in Southern Brazil with particular reference to fungal pathogens for biological control. Mycological Research, 99(3), 343–352.
BHUJU, U. R., Shakya, P. R., Basnet, T. B., Shrestha, S. (2007). Nepal biodiversity resource book: protected areas, Ramsar sites, and World Heritage sites. International Centre for Integrated Mountain Development (ICIMOD). Retrieved from https://www.cabdirect.org/cabdirect/abstract/20073209405.
BOHENSKY, E. (2014). Learning dilemmas in a social-ecological system: An agent-based modeling exploration. Journal of Artificial Societies and Social Simulation, 17(1), 2: https://www.jasss.org/17/1/2.html. [doi:10.18564/jasss.2448 ]
BOHRA, P., & Massey, D. S. (2009). Processes of Internal and International Migration from Chitwan, Nepal. The International Migration Review, 43(3), 621–651. [doi:10.1111/j.1747-7379.2009.00779.x]
BONABEAU, E. (2002). Agent-based modeling: Methods and techniques for simulating human systems. Proceedings of the National Academy of Sciences, 99(suppl 3), 7280–7287.
BROEKHUIZEN, T. L. J., Delre, S. A., & Torres, A. (2011). Simulating the Cinema Market: How Cross-Cultural Differences in Social Influence Explain Box Office Distributions. Journal of Product Innovation Management, 28(2), 204–217. [doi:10.1111/j.1540-5885.2011.00792.x]
BURGER, J., Ostrom, E., Norgaard, R., Policansky, D., & Goldstein, B. D. (2001). Protecting the Commons: A Framework For Resource Management In The Americas (1 edition). Washington, D.C: Island Press.
CALDAS, J. C., & Coelho, H. (1999). The Origin of Institutions: socio-economic processes, choice, norms and conventions. Journal of Artificial Societies and Social Simulation, 2(2), 1: https://www.jasss.org/2/2/1.html.
CAMPBELL, J. L. (2004). Institutional Change and Globalization. Princeton, NJ: Princeton University Press.
CHARNLEY, S., & Poe, M. R. (2007). Community Forestry in Theory and Practice: Where Are We Now? Annual Review of Anthropology, 36, 301–336. [doi:10.1146/annurev.anthro.35.081705.123143]
CRAWFORD, S. E., & Ostrom, E. (1995). A grammar of institutions. American Political Science Review, 89(03), 582–600.
DEAN, J., Gumerman, G., Epstein, J., Axtell, R., Swedlund, A., Parker, M., & McCarroll, S. (2000). 'Understanding Anasazi culture through agent-based modeling.' In T. Kohler & G. Gummerman (Eds.), Dynamics in Human and Primate Societies: Agent-Based Modeling of Social and Spatial Processes (pp. 179-205). Oxford, UK: Oxford University Press.
DIETZ, T., Ostrom, E., & Stern, P. C. (2003). The Struggle to Govern the Commons. Science, 302(5652), 1907–1912. [doi:10.1126/science.1091015 ]
EPANCHIN-NIELL, R. S., Hufford, M. B., Aslan, C. E., Sexton, J. P., Port, J. D., & Waring, T. M. (2010). Controlling invasive species in complex social landscapes. Frontiers in Ecology and the Environment, 8(4), 210–216. [doi:10.1890/090029]
ESTEVEZ, R. A., Anderson, C. B., Pizarro, J. C., & Burgman, M. A. (2015). Clarifying values, risk perceptions, and attitudes to resolve or avoid social conflicts in invasive species management. Conservation Biology, 29(1), 19–30. [doi:10.1111/cobi.12359 ]
FOLKE, C., Pritchard, L., Berkes, F., Colding, J., & Svedin, U. (2007). The problem of fit between ecosystems and institutions: ten years later. Ecology and Society, 12(1), 30. [doi:10.5751/ES-02064-120130]
GHORBANI, A., Dijkema, G., & Schrauwen, N. (2015). Structuring qualitative data for agent-based modelling. Journal of Artificial Societies and Social Simulation, 18(1), 2: https://www.jasss.org/18/1/2.html. [doi:10.18564/jasss.2573 ]
GILMOUR, D. (2003). Retrospective and prospective view of community forestry in Nepal. Journal of Forest and Livelihood, 2(2), 5–7.
GRATANI, M., Butler, J. R. A., Royee, F., Valentine, P., Burrows, D., Canendo, W. I., & Anderson, A. S. (2011). Is Validation of Indigenous Ecological Knowledge a Disrespectful Process? A Case Study of Traditional Fishing Poisons and Invasive Fish Management from the Wet Tropics, Australia. Ecology and Society, 16(3), 25. [doi:10.5751/ES-04249-160325 ]
GRIMM, V., Berger, U., Bastiansen, F., Eliassen, S., Ginot, V., Giske, J., Goss-Custard, J., Grand, T., Heinz, S. K., Huse, G., Huth, A., Jepsen, J. U., Jørgensen, C., Mooij, W. M., Müller, B., Pe’er, G., Piou, C., Railsback, S. F., Robbins, A. M., Robbins, M. M., Rossmanith, E., Rüger, N., Strand, E., Souissi, S., Stillman, R. A., Vabø, R., Visser, U. DeAngelis, D. L. (2006). A standard protocol for describing individual-based and agent-based models. Ecological Modelling, 198(1–2), 115–126. [doi:10.1016/j.ecolmodel.2006.04.023]
GRIMM, V., Berger, U., DeAngelis, D. L., Polhill, J. G., Giske, J., & Railsback, S. F. (2010). The ODD protocol: a review and first update. Ecological Modelling, 221(23), 2760–2768. [doi:10.1016/j.ecolmodel.2010.08.019 ]
HAYEK, F. (1978). Law, Legislation and Liberty, Volume 1: Rules and Order. Chicago: University of Chicago Press. [doi:10.7208/chicago/9780226321233.001.0001]
HEARD, D., Dent, G., Schifeling, T., & Banks, D. (2015). Agent-Based Models and Microsimulation. Annual Review of Statistics and Its Application, 2(1), 259–272 [doi:10.1146/annurev-statistics-010814-020218 ]
HELMKE, G., & Levitsky, S. (2004). Informal Institutions and Comparative Politics: A Research Agenda. Perspectives on Politics, 2(04), 725–740. [doi:10.1017/S1537592704040472]
HENRICH, J., Heine, S. J., & Norenzayan, A. (2010). The weirdest people in the world? The Behavioral and Brain Sciences, 33(2-3), 61–83; discussion 83–135. [doi:10.1017/S0140525X0999152X ]
HUIGEN, M., Overmars, K., & de Groot, W. (2006). Multiactor modeling of settling decisions and behavior in the San Mariano watershed, the Philippines: A first application with the MameLuke framework. Ecology and Society, 11(2), 33. [doi:10.5751/ES-01738-110233]
JANSSEN, M. A., & Ostrom, E. (2006). Empirically based, agent-based models. Ecology and Society, 11(2), 37.
KANTOR, S. (1998). Politics and Property Rights: The Closing of the Open Range in the Postbellum South (1 edition). Chicago: University Of Chicago Press.
KELLER, R. P., Cadotte, M. W., & Sandiford, G. (Eds.). (2014). Invasive Species in a Globalized World: Ecological, Social, and Legal Perspectives on Policy. Chicago: University Of Chicago Press.
KINGSTON, C., & Caballero, G. (2009). Comparing theories of institutional change. Journal of Institutional Economics, 5(02), 151–180. [doi:10.1017/S1744137409001283]
LIBECAP, G. (1994). Contracting for Property Rights. Cambridge, MA: Cambridge University Press.
LOZANO, S., & Maes, M. (2008). Axelrod-culture NetLogo model. NetLogo. Retrieved from https://www.openabm.org/book/3138/114-diffusion-culture.
MAGLIOCCA, N. R., Shelley, M., & Smorul, M. (2015). Agent-based virtual laboratories for a novel experimental approach to socio-environmental syntheses. In International Environmental Modelling and Software Society (iEMSs). Retrieved from https://www.sesync.org/agent-based-virtual-laboratories-for-a-novel-experimental-approach-to-socio-environmental-syntheses.
MAHONEY, J., & Thelen, K. (2010). Explaining Institutional Change: Ambiguity, Agency, and Power. Cambridge University Press.
MASSEY, D. S., Axinn, W. G., & Ghimire, D. J. (2010). Environmental change and out-migration: evidence from Nepal. Population and Environment, 32(2-3), 109–136.
MATHEW, S., & Perreault, C. (2015). Behavioural variation in 172 small-scale societies indicates that social learning is the main mode of human adaptation. Proceedings of the Royal Society B, 282(1810), 20150061. [doi:10.1098/rspb.2015.0061]
MAZZOCCHI, F. (2006). Western science and traditional knowledge: Despite their variations, different forms of knowledge can learn from each other. EMBO Reports, 7(5), 463–466.
MOSS, S. (2008). Alternative Approaches to the Empirical Validation of Agent-Based Models. Journal of Artificial Societies and Social Simulation, 11(1), 5: https://www.jasss.org/11/1/5.html.
MURPHY, S. T., Subedi, N., Jnawali, S. R., Lamichhane, B. R., Upadhyay, G. P., Kock, R., & Amin, R. (2013). Invasive mikania in Chitwan National Park, Nepal: the threat to the greater one-horned rhinoceros Rhinoceros unicornis and factors driving the invasion. Oryx, 47(03), 361–368.
NAGENDRA, H., & Southworth, J. (2009). 'Reforestation and Regrowth in the Human Dominated Landscapes of South Asia.' In W. Jager, R. Verbrugge, A. Flache, G. de Roo, L. Hoogduin, & C. Hemelrijk (Eds.), Reforesting Landscapes: Linking Pattern and Process. Dordrecht: Springer, pp. 149-174. [doi:10.1007/978-1-4020-9656-3_7]
NIGHTINGALE, A. J. (2005). “The Experts Taught Us All We Know”: Professionalisation and Knowledge in Nepalese Community Forestry. Antipode, 37(3), 581–604.
NORTH, D. C. (1990). Institutions, Institutional Change and Economic Performance. Cambridge ; New York: Cambridge University Press. [doi:10.1017/CBO9780511808678]
OSTROM, E. (1990). Governing the Commons: The Evolution of Institutions for Collective Action. Cambridge: Cambridge University Press.
OSTROM, E. (2005). Understanding institutional diversity. Princeton, NJ: Princeton University Press.
OSTROM, E., Gardner, R., & Walker, J. (1994). Rules, Games, and Common-pool Resources. Michigan, MA: University of Michigan Press.
PARKER, M. J., Manan, A., & Urbanski, S. (2012). Prospective evaluation of direct approach with a tablet device as a strategy to enhance survey study participant response rate. BMC Research Notes, 5(1), 605. [doi:10.1186/1756-0500-5-605]
RAI, R. K., & Scarborough, H. (2015). Understanding the effects of the invasive plants on rural forest-dependent communities. Small-scale forestry, 14(1), 59-72.
RAILSBACK, S. F., & Grimm, V. (2011). Agent-Based and Individual-Based Modeling: A Practical Introduction. Princeton: Princeton University Press.
RAISER, M. (1997). Informal institutions, social capital and economic transition: Reflections on a neglected dimension. European Bank for Reconstruction and Development, EBRD Working Paper n. 25.
RICHERSON, P., & Henrich, J. (2012). Tribal Social Instincts and the Cultural Evolution of Institutions to Solve Collective Action Problems. Cliodynamics: The Journal of Theoretical and Mathematical History, 3(1): 38-80.
SCHUETTLER, E., Rozzi, R., & Jax, K. (2011). Towards a societal discourse on invasive species management: A case study of public perceptions of mink and beavers in Cape Horn. Journal for Nature Conservation, 19(3), 175–184.
STIVALA, A., Robins, G., Kashima, Y., & Kirley, M. (2014). Ultrametric distribution of culture vectors in an extended Axelrod model of cultural dissemination. Scientific Reports, 4, 4870. [doi:10.1038/srep04870]
SULLIVAN, A., York, A. M., An, L., Yabiku, S. T., & Hall, S. J. (2017a). How does perception at multiple levels influence collective action in the commons? The case of Mikania micrantha in Chitwan, Nepal. Forest Policy and Economics, 80, 1–10.
SULLIVAN, A., York, A., White, D., Hall, S., & Yabiku, S. (2017b). De jure versus de facto institutions: trust, information, and collective efforts to manage the invasive mile-a-minute weed (Mikania micrantha). International Journal of the Commons, 11(1), 171–199. [doi:10.18352/ijc.676]
TEN Broeke, G., van Voorn, G., & Ligtenberg, A. (2016). Which Sensitivity Analysis Method Should I Use for My Agent-Based Model? Journal of Artificial Societies and Social Simulation, 19(1), 5: https://www.jasss.org/19/1/5.html. [doi:10.18564/jasss.2857 ]
VALLINO, E. (2014). The Tragedy of the Park: an Agent-based Model of Endogenous and Exogenous Institutions for Forest Management. Ecology and Society, 19(1), 35. [doi:10.5751/ES-06242-190135]
VEBLEN, T. (1899). The Theory of the Leisure Class: An Economic Study in the Evolution of Institutions. Chestnut Hills, MA: Adamant Media Corporation.
WHITE, A., & Martin, A. (2002). Who owns the world's forests? Forest tenure and public forests in transition. Forest Trends, Washington, D.C. Retrieved from http://www.cifor.org/publications/pdf_files/reports/tenurereport_whoowns.pdf.
WILENSKY, U. (1999). NetLogo. Northwestern University, Evanston, IL: Center for Connected Learning and Computer-Based Modeling. Retrieved from http://ccl.northwestern.edu/netlogo/.
WILLIAMSON, O. E. (2000). The New Institutional Economics: Taking Stock, Looking Ahead. Journal of Economic Literature, 38(3), 595–613. [doi:10.1257/jel.38.3.595]
YANG, L., & Gilbert, N. (2008). Getting away from numbers: using qualitative observation for agent-based modeling. Advances in Complex Systems, 11(02), 175–185.
YOUNG, H. P. (1996). The Economics of Convention. The Journal of Economic Perspectives, 10(2), 105–122. [doi:10.1257/jep.10.2.105]
YOUNG, O. (2002). The Institutional Dimensions of Environmental Change. Cambridge, MA: The MIT Press.
ZHANG, H., & Vorobeychik, Y. (2016). Empirically Grounded Agent-Based Models of Innovation Diffusion: A Critical Review. arXiv Preprint arXiv:1608.08517. Retrieved from https://arxiv.org/abs/1608.08517.
