Agent-Based Models of Gender Inequalities in Career Progression

Introduction

There has been considerable concern and discussion for many years now about the significant gender imbalances currently present in certain professions and sections of academia, such as university physics, philosophy and computer science departments (Allen-Hermanson 2017; Altonji & Blank 1999; Beyer 2014; Camp 1997; Cheryan et al. 2017; Handelsman et al. 2005; Moss-Racusin et al. 2012). So, given the evidence indicating that gender diversity is associated with improved decision making and problem solving (Handelsman et al. 2005) and increased sales and profits (Herring 2009), and the obvious potential for critical skills shortages if one gender is excluded (Camp 1997), it is not surprising that various strategies have been suggested for rectifying such imbalances. Previous approaches have ranged from various forms of positive discrimination, through specific types of advertising and re-education, to simply adopting more gender-fair language (Sczesny et al. 2016). However, when it is not clear what are the main causes underlying the imbalances (Beasley & Fischer 2012; Beyer 2014; Blickenstaff 2005; Cheryan et al. 2017; Halpern et al. 2007; Wang & Degol 2014; Wang et al. 2013; Williams & Ceci 2015), it can be difficult to identify the best strategies for dealing with them and measuring their effect, and there is also a persistent worry that adopting particular intervention strategies predicated on incorrect assumptions might actually make matters worse rather than better.

It is often claimed that the main cause of gender imbalance is simple discrimination against a particular gender (Davison & Burke 2000; Moss-Racusin et al. 2012), and if that cannot be prevented, an appropriate remedy would be some form of positive discrimination. However, other studies indicate that, in some cases at least, there is no such bias in the hiring processes (Allen-Hermanson 2017; Williams & Ceci 2015). Another potential cause of imbalance might be that evolution by natural selection has led to different genders becoming specialized for different roles, and hence intrinsically more able or less able in particular areas. It is undoubtedly true that there exists significant gender-based physical differences for many species, such as human men being bigger and stronger on average than human women, but associated differences in intellectual abilities are more controversial. In particular, there is conflicting evidence concerning gender-based brain-related ability differences in humans, and their potential impact on gender inequalities in professions such as computer science (Baron-Cohen 2004; Benbow 1988; Browne 2002; Cahill 2006; Geary 1998; Halpern 2012; Halpern et al. 2007; Kimura 2000; Spelke 2005). With fair performance-led hiring and promotion, any such ability differences leading to inferior performance would inevitably result in less success in any professions that rely on those skills, and that could drive a consequent tendency for that gender to avoid entering related professions in the future. In fact, even when both genders have equal average abilities, differences in the tails of the ability distributions can be sufficient to drive significant gender imbalances (Humphreys 1988; Wai et al. 2010). Moreover, even when there are no intrinsic ability differences at birth, there could still be cultural factors that lead to ability differences in adults, such as those arising from biases in the education system (Else-Quest et al. 2010; Hyde & Mertz 2009). It is not at all clear what interventions would be most beneficial for particular types of ability difference, nor whether any intervention at all would be a sensible strategy. A final possibility is that, even when there is no direct discrimination, and no ability differences in the chosen area, one gender might still be disadvantaged by other factors, such as delays in career progression related to child rearing and maternity leave (Ceci & Williams 2011), and such causes of gender imbalance are likely to require different forms of intervention.

An obvious approach for understanding gender imbalances, or other diversity issues, within complex interacting processes is to build computer simulations of them (Helbing 2010; Martell et al. 1996; Robison-Cox et al. 2007). That allows models of the core issues to be formulated without all the confounding factors and complications of real life, and strategies for intervention can be explored and optimized before inflicting them on real people. What appears to be less widely appreciated is that agent-based simulations of populations of individuals with ability-based selection are commonly used in the fields of computational intelligence (Engelbrecht 2007) and artificial life (Bullinaria 2009, 2017) and provide a particularly effective approach for exploring the key causes, effects and remedies here. Such models also have the significant advantage that the evolution of any relevant factors and memes by processes of natural selection can be implemented straightforwardly within the same framework. Moreover, by building on tried and tested existing models, the various methodological pitfalls that often arise with agent-based simulations of social and economic scenarios (Galán et al. 2009; Richiardi et al. 2006) can be avoided more easily. This paper therefore proposes a general framework for formulating and optimizing such models, and presents a selection of simulation results for various abstract scenarios that illustrate the potential of the approach.

The remainder of this paper is organized as follows: The next section describes the underlying simulation framework with its associated simplifications and assumptions. Then results from a series of preparatory baseline models are presented that identify appropriate values for the various free parameters. The following two sections establish how the outcomes vary with the introduction of either gender-based ability differences or discrimination. Then, the effect of simple gender-balancing interventions are investigated, and how gender-specific profession preferences might emerge. Finally, the practical consequences of the various inequalities and intervention strategies are explored in more detail. The paper ends with some discussion and conclusions.

Underlying Assumptions and Simulation Framework

There is an inevitable trade-off involved when deciding on the best level of detail to use in agent-based models. On one hand it makes sense to keep the models as simple and abstract as possible in order to observe general patterns of outcomes with minimal confounding factors, but on the other there are advantages to validating detailed models using all the available empirical data including as many potentially confounding factors as possible (Edmonds & Moss 2005). The aim here is to present an abstract and general modelling framework that others can later employ to simulate specific aspects of interest to them more accurately by incorporating additional factors. One reason for this is that there is a recurring difficulty with real empirical data in this area in that it can often be equally well modelled with radically different assumptions about the underlying issues, and making particular assumptions opens up the work to potential bias which is important to avoid. In fact, one of the key aims of this paper is to show how similar outcomes can emerge in rather different ways, and how particular signals can be identified that narrow down what underlying issues are causing the observed outcomes. Moreover, a number of simplifications and assumptions will be required to render the simulations computationally feasible, reliably interpretable, and as unbiased as possible (Bullinaria 2009, 2017). So this study will begin by setting a few basic principles, and then go on to explore what can emerge within that general framework.

The underlying idea is to maintain evolving populations of individuals, with a range of gender-specific ability differences and profession preferences (both potentially involving innate and culturally-acquired components), who compete with each other during their lifetimes to be promoted up through the hierarchy of their chosen professions. Thus, with the aim of avoiding as many unnecessary biases and confounding factors as possible, the following modelling assumptions will be adopted:

1. There are two distinct genders, which are determined randomly at birth with equal probability.
2. Overall, the two genders are equally able, but different gender-specific distributions of individual abilities may exist. The differences could be innate, resulting from the evolutionary past, or culturally-acquired. In this paper, these distributions will be fixed for the duration of each simulation, but they may be allowed to evolve in future models of the emergence of such gender differences.
3. There are two distinct professions, which overall are equally valuable.
4. The initial individual abilities related to each profession are determined randomly on entering the simulation and follow normal (Gaussian) distributions. The means and/or the standard deviations of those distributions may depend on gender, or they may be independent of gender.
5. If one gender has better ability in one profession, the other gender will have an equally better ability in the other. The effect of the type and magnitude of such differences is one of the key factors to be explored.
6. A range of profession choice strategies may exist. Each individual could choose their profession totally randomly, or according to their abilities, or have some innate or culturally-acquired gender-based preference (or probability) for choosing one profession over the other. Such preferences may be allowed to emerge during the course of the simulations.
7. During each simulation, the individuals inevitably get older, potentially improve their abilities as a result of experience in their chosen profession, and eventually retire and leave the working population.
8. Professional development involves a series of stages, and (by default) promotion between them is given to the most able of the individuals currently eligible at each stage (Rosenbaum 1979). Discrimination and intervention in that process are key factors to be explored.
9. If an individual does not get promoted within a reasonable number of simulated years, they may give up and leave their profession or working population. It is also possible that varying percentages of individuals leave their profession or working population for other reasons. These are further details that need to be explored.
10. The working population size is kept constant by replacing retired individuals with new young individuals. The success of the retired individuals in their chosen profession may influence the profession choices of the new individuals.

These assumptions may seem rather restrictive, but they prove suitable for the purposes of this initial study, and simplify the interpretation of the results. There is still considerable scope for variations within this basic framework, and a sufficient variety of different outcomes can emerge from it depending on the relative settings of the various parameters involved. There is also plenty of scope to design variations that test the consequences of these initial simplifications, and to make the simulations more realistic.

All the simulations will follow fairly standard agent-based modelling procedures, with a random initial population, repeated updates over time that include promotion opportunities, and retired individuals being replaced by new individuals. For each new individual entering the simulated population, a record is created and initialized with their innate gender, initial age, entry-level abilities for the two professions, any preferences for the professions, and their chosen profession. Thereafter it is regularly updated with their current age, stage in their profession, number of years since reaching that stage, and any experience-related ability changes. After updating the population for a sufficient number of simulated years, all the population averages eventually settle down into a steady state, and the relevant results can be computed. This underlying data and simulation structure is specified in more detail in the Appendix.

The above framework has been designed to be general enough that it can be used to simulate “professions” and associated hierarchies of all kinds. For example, with suitable modifications of the “promotion” processes it could be used to model the kinds of dominance hierarchies found in many animal species (Chase 1974; Hobson & DeDeo 2015). Often animal societies will only involve a single role that covers everything, but some species do have clear divisions of labour, such as food provision versus offspring care and defence in wolf packs (Mech 1999), and those distinct roles could be modelled in the same way as more traditional professions. However, this paper will concentrate on the particular scenario that originally motivated it, and only consider abstract human professions, with human-like lifetimes and other parameters.

To simplify the results analysis, it will be assumed that all individuals enter their chosen profession at age 20 and retire at age 70, and that each profession has 7 stages, so 6 promotions are required to reach the highest stage. Depending on the aims of the model, stage 1 could be interpreted as the pool of applicants wanting to join the profession, with stage 2 the lowest level within the profession, or stage 1 could be the lowest level within the profession. Then a workable update frequency for reasonably realistic simulations of 50 year careers is once per simulated year. It will initially be assumed that there is only one employer for each profession, so there is no need to simulate transfers between employers, or sub-groups of eligible individuals being considered at each promotion stage, as that is already known to bias the results (Lyness & Judiesch 1999). The general framework is deliberately flexible enough that it will allow more realistic scenarios to be modelled in more detail in the future. For reasonable parameter values, a population size of 10,000 provides sufficient numbers of individuals per profession per stage per gender to allow realistic levels of competition at each stage, even when the distributions become skewed. Since only relative abilities affect anything, the ability scale is measured in arbitrary units, and that is set (without loss of generality) by taking the standard deviation of the initial Gaussian distributions to be 1.0, and measuring all the ability differences relative to that. When the abilities are plotted, they are given a convenient mean of 8.0, but the same ability differences would emerge for any other mean value.

How many simulated years to run each simulation is not obvious. Real life professional developments will rarely have lasted more than a few hundred years, and most are much shorter than that. However, the simulations will normally need to be run for a sufficient number of simulated years that the populations settle down into a stable final state that is independent of the initial conditions which could potentially introduce unintentional biases. That varies somewhat with the various parameter values involved, and checking for stability and stopping each run at a different point introduces unnecessary complications that can be avoided by simply running all the simulations for the same number of simulated years that is considerably more than required to reach stability even in the most extreme of situations. Moreover, some of the simulations involve the evolution of innate traits which takes place over much longer timescales than those of human career structures. The actual run length used to guarantee stability throughout was 10,000 simulated years. Much shorter realistic-length runs will in some cases end in the same stable state, but in others the same length run will end in a state that is still changing and biased by the initial conditions. Either of those shorter run cases may well correspond to what we are currently observing in real populations, but to compare outcomes fairly it is necessary to be sure that an unbiased stable state has been reached. Naturally, being more careful about the initial conditions and looking at the stabilization process over more realistic timescales will certainly be worth attempting in the future.

Updating all the individual ages, applying any ability increments, and replacing the retired and removed individuals is straightforward. However, there are several potential approaches for dealing with the promotions between the stages of each profession, so that requires further specification. How ranks or dominance hierarchies generally form in animal societies remains a matter of some debate and probably depends on the species in question (Chase 1974; Hobson & DeDeo 2015). However, for the kinds of human careers of interest here, it is reasonable to assume that there are regular selection processes to determine which individuals are promoted up the hierarchy, and demotions are rare enough that they can be ignored, at least in the initial simulations. One obvious possibility is to maintain pre-defined numbers at each stage to correspond to the hierarchies of typical companies (Robison-Cox et al. 2007). An alternative and more flexible approach, that is adopted here, promotes a given fraction x of the eligible individuals at each stage in each profession each year. Then, requiring a minimum number of years w working at each stage before becoming eligible for promotion, having individuals give up waiting for promotion after a certain number of years g at one stage, and the promotion fraction x itself, are factors that will need to be specified to match particular realistic scenarios. A fair implementation of the promotions would rank the N eligible individuals at each profession stage according to their current abilities, and promote the top xN of them. However, there also needs to be potential for having direct discrimination in the promotion criteria, as well as various types of indirect discrimination. Of course, the whole point of the models is to be able to introduce parameterized versions of all the various forms of ability differences, discriminations and interventions that might be deemed relevant, so their emergent consequences can be explored empirically.

The output of each simulation will generally be the final population of individuals, each with a gender, age, preference for profession, profession, ability in their chosen profession, and profession stage. The main factors of interest will usually be the various differences in the population means between genders, such as how the profession preferences and numbers at each profession stage depend on gender (Robison-Cox et al. 2007). When looking at the effect of the various intervention strategies, it may instead be the overall performance of the whole population that is important, rather than what is happening with particular genders. In some situations, it may not be the stable final population that is most interesting, but the changes that occur in the associated parameter values, such as the profession preferences, throughout the simulation. In all cases, to obtain reliable results, means and standard deviations are computed from thirty independent runs of each simulation (using different random number seeds), with unpaired t tests used to determine the statistical significances of any differences found.

The computer simulations proposed here will show the outcomes of the various scenarios studied, but they will only be useful in practice if they can be tied to particular real-life scenarios, at least in the sense of some form of general-case approximation. There is certainly evidence that gender-based inequalities do exist in real human professions, and, in the absence of clear evidence of underlying ability differences, it tends to be assumed that they must result from some kind of discrimination. A key advantage of the simulations is that they are not tied to the properties of real populations, so the effects of both ability differences and discrimination can be separated and tested independently, with larger than real-life magnitudes that render the effects much easier to observe. In that way, the simulations will be able to reveal distinct observable signals in the outcomes that can provide a basis for indirect empirical testing of the hypothesized causes of the imbalances in real populations, and hence lead to better informed decisions concerning appropriate remedial actions.

Baseline Models and Parameters

The approach adopted here is to first establish some baseline results using the simplest possible simulation set-up, and then systematically investigate how the potential variations affect those results. Such a sequential approach also facilitates the setting of the various parameter values at each stage.

The baseline case has no gender differences, no experience-related ability increases, and simply has the most able individuals promoted at each stage, with an equal promotion fraction x at each stage. The resulting numbers of individuals at each profession stage are shown in Figure 1, for five values of x ranging from 0.01 to 0.05. For very small x values (0.01 and below), no individuals ever reach the upper stages, which is clearly unrealistic. For high values (0.04 and above), there are more in the highest stage than in some of the lower stages, which might correspond to the large numbers of full professors found in some academic departments. Values around 0.02 to 0.03 probably come closest to most realistic situations in academia or industry, where there is a pyramid structure with fewer individuals as one moves up the hierarchy (Robison-Cox et al. 2007; Rosenbaum 1979). To simulate some real-life scenarios, different promotion fractions x_s for each stage s might be required, and that can easily be included in the models, though, for simplicity, the following will continue with a single value x for all stages.

In practice, the longer an individual has been at a given stage of their profession, the more expertise and experience they are likely to have acquired, and the more likely they are to be promoted. One way to model that would be to have the overall ability increase with time at each stage, though this is complicated by the fact that in reality the more able individuals are likely to be able to increase their ability more quickly than others, and the less able individuals may never be able to reach a promotable standard. This could all be implemented, of course, but another reasonable and more straightforward approach, that will be adopted here, is to simply require all individuals to spend a certain minimum number of years at each stage to acquire enough additional expertise to become eligible for promotion. That is easier to model, but will need a higher proportion x of eligible individuals to be promoted each year to fill the higher stages. For a promotion fraction x of 0.06, the effect of varying the number of years w waiting for eligibility from 0 to 8 is shown in Figure 2. For 0 years, that promotion fraction is too high, as seen in Figure 1. Waits w of around 6 or 7 years are probably typical for many professions and lead to the kind of pyramidal distribution of individuals across the stages familiar in many organizations.

A related variation models the fact that some individuals are simply not good enough to get very far within their chosen profession, and giving up and leaving is probably a sensible strategy for them, particularly if stage 1 is being interpreted as the pool of applicants rather than the entry level of the profession. In reality, what actually happens will depend on the profession in question, and leaving for this reason is likely to be more common at the lower stages, than at the higher stages, but the effect can be approximated by simply giving up and leaving the profession if any promotion is not achieved within a certain number of years g after becoming eligible. In practice, there will be individual differences in this matter, so a distribution of g values would be more appropriate than a single fixed value, and such distributions could potentially also depend on gender as well as profession stage. Those complications could easily be simulated, but, to simplify the analysis, they will be left for future studies, and a single fixed value used for g here. In that case, a slightly shorter wait w is needed to have sufficient numbers eligible for promotion at each stage. Then, with a promotion fraction of 0.06 and a 4 years wait for eligibility, the effect of varying the number of years g before giving up from 4 to 32 is shown in Figure 3. For a tolerant 32 years, there is little difference from never giving up. For fewer years, there are inevitably more drop-outs and the numbers at the later stages fall more sharply, and since there is a fixed total number of individuals in the profession, that means more at stage 1.

There are clearly more details that could be modelled, but having established how the three main promotion parameters (x, w, g) affect the distribution across stages, explorations of the effect of gender differences can now begin. Obviously, the various parameters will need to be set to different appropriate values depending on the professions in question, and even then they will only be able to offer an approximate representation of real-life scenarios. For the purposes of exhibiting the general trends that might typically emerge, a set of typical values will suffice. Moreover, the actual parameter values chosen tend to be less important for the qualitative patterns of simulation outcomes than the distribution of individuals across stages they lead to, though precise values will become crucial if more realism requires there to be gender differences in them. The baseline simulations have indicated that a promotion fraction x = 0.06, a wait for eligibility w = 4 years, and a wait before giving up g = 12 years, provides a reasonably realistic starting point for the forthcoming simulations. Varying those key values by small amounts will change the detailed results, but the general emergent patterns are unaffected.

Gender-Based Ability Differences

Obviously, to explore the effect of gender-based ability differences, those differences must first be built into the models, and then separate resulting stage distributions need to be computed for the two genders (Gen0 and Gen1). As noted above, there is no dispute that different genders of many species, including humans, have different ability levels for some tasks. However, for the intellectual skills underlying many careers in industry or academia, the ability differences are more controversial (Benbow 1988; Else-Quest et al. 2010; Geary 1998; Halpern 2012; Halpern et al. 2007; Spelke 2005). Nevertheless, it is possible to avoid making any controversial assumptions about them by keeping the models suitably abstract, and attempting to use their outcomes to establish how well they might correspond to particular real-life scenarios. At this stage, there is no need to specify whether the ability differences are innate, resulting from evolution by natural selection, or culturally acquired such as via stereotyping in biased educational systems (Lane et al. 2012; Van der Heyden et al. 2016). Further simulations could help with untangling that distinction, but that is something else which will be left for future work. A convenient starting point, with easily observable differences, has the mean ability levels associated with a particular profession differ by one standard deviation (Dif 1) between genders, and compares that with the baseline case above that has zero gender difference (Dif 0).

Figure 4 shows what happens within one particular profession for the simplest case in which each individual chooses one of the two professions totally at random, irrespective of their ability or gender. Naturally, there is no significant gender difference in the zero ability difference (Dif 0) case. When there is a difference (Dif 1), the more able gender (Gen0) for the given profession not surprisingly has more individuals at the higher stages, and fewer stuck at the initial stage. The associated increased tendency for the less able gender to give up waiting for promotion and drop out also gives rise to differences in the total number of each gender participating in the profession. For this profession in the Dif 1 case there are 2746 (std. dev. 39) of the more able Gen0 and only 2276 (std. dev. 40) of Gen1, which is a significant difference (t test, p < 10^-46). For Dif 0, there are 2511 (std. dev. 54) of Gen0 and 2496 (std. dev. 46) of Gen1, with no significant difference (t test, p = 0.26).

If all individuals instead stayed in their randomly chosen profession till retirement, even if they became stuck at a low level, there would clearly be no significant differences in the total number of each gender in each profession, even in the case of gender-based ability differences, with 5004 (std. dev. 50) versus 4996 (std. dev. 50) and t test p = 0.57. That leads to the slightly different distribution across stages shown in Figure 5, with larger proportions of the weaker gender at the lower stages, but the general pattern of gender differences remains the same. It may be more appropriate here to consider stage 1 as the pool of applicants, and only stage 2 and above as being within the profession, and it is noticeable that stages 2 to 7 in Figure 5 look a lot like stages 1 to 7 in Figure 4. In that case, gender-based ability differences do again lead to gender differences in the numbers in each profession: for the Dif 1 case there are 1982 (std. dev. 51) of the more able Gen0 and only 1395 (std. dev. 33) of Gen1, which is a significant difference (t test, p < 10^-44). Since there are similar outcomes for the giving-up and not-giving-up cases, only the giving-up case of Figure 4 will be pursued for the remainder of this paper, and to aid comparisons the same key parameter values will be used throughout (i.e., x = 0.06, w = 4, g = 12), but it should be borne in mind there do exist variations that may have subtle differences in outcome and interpretation.

In reality, very few individuals will choose their profession totally randomly. Instead, they will tend to choose a profession according to their abilities, and when the extreme case of simply choosing the profession matching their best ability is built into the models, the outcome changes somewhat to that shown in Figure 6. Again there is no significant gender difference for the Dif 0 case (t test, p = 0.47), but for Dif 1 there is an even bigger statistically significant (t test, p < 10^-84) reduction in the number of Gen1 individuals choosing the profession, 1114 (std. dev. 44) compared to 3893 (std. dev. 52) for Gen0. Figure 7 compares the Dif 1 outcomes for random choice of profession (rand) and ability-based choice of best profession (best), as percentages of the whole population of each gender at each stage in the profession. The ability-based choice of profession brings the gender distributions closer together, but the less able Gen1 still has much reduced numbers at the higher stages compared to Gen0.

Another informative way to present the simulation results is in terms of the percentages of each gender at each stage within one particular profession. Since these percentages always add up to 100%, it is sufficient to show the results for only one gender (Gen1). These are shown in Figure 8 for both the random and best profession choice cases. When there is no gender difference (Dif 0), the percentage of Gen1 at each stage is not significantly different from 50%. For Dif 1 with random profession choice, the proportion at stage 1 is slightly over 50% (due to weaker individuals waiting there for a promotion that never comes) and then falls for later stages. When the best profession is chosen by each individual, there is a lower starting point, and a slower fall off at later stages, but the numbers remain lower at all stages compared to the random choice case. Thus, a gender-based ability difference results in percentage differentials that increase with stage even when self selection leads to reduced participation of the less able gender. This kind of pattern, known as a shrinking pipeline, is known to exist in real populations (Camp 1997; Gürer & Camp 2001; Walker & Rodger 1996), but not necessarily for the same reason (Allen-Hermanson 2017; Bennett 2011; Blickenstaff 2005), and there is also evidence of recent improvements in this regard (Miller & Wai 2015; Schreuders et al. 2009).

One of the advantages of computer simulations is that the various potential causes of the pipeline differences can be explored without all the confounding factors inherent in real populations, so signals can be identified in the results that might allow us to distinguish between the potential causes. For example, shrinking pipelines can also arise even when there is no difference in the mean abilities of the two genders. If the variance in abilities for one gender is less than that of the other, as appears to be the case for some human skills (Humphreys 1988; Wai et al. 2010), that can give the higher variance gender an advantage at the later promotion stages, even if the means are the same for each gender. Figure 9 shows the effect of Gen1 having equal mean ability but only half the ability variance of Gen0, for both the random and best choices of profession. The clear difference between the shrinking pipelines observed in Figures 8 and 9 constitute a signal that can be looked for in real pipelines, and that can then be used to provide insights into the underlying causes. However, this may not be totally straightforward in practice, since care will be needed to accurately map the simulation stages to real stages, and the abilities of real populations could well involve various combinations of mean and variance differences that leave the signals less sharply defined and harder to observe.

It is clear already that there are many potential types of gender differences in ability, both innate and culturally acquired, that could account for the unequal gender distributions observed in real professions. From the modelling point of view, there remains scope to add further realism by replacing the simple Gaussian distributions of abilities used so far with something more accurate, but determining exactly what those improved distributions should be will probably not be easy (Benbow 1988; Halpern et al. 2007; Spelke 2005; Wai et al. 2010), and using them is unlikely to change the broad pattern of results anyway. Of course, the important issue here is that the observed gender inequalities can also occur when there are no ability differences at all, and that is what will be investigated next.

Gender-Based Discrimination

Probably the question of most practical importance here is whether similar patterns of gender inequalities can emerge when, rather than there being ability differences, there is discrimination against a particular gender. Given the range of possibilities, it will clearly not be feasible to study in detail all the potential types of discrimination here, but, from the modelling point of view, there is actually no need to consider the precise details, nor the underlying reasons for them. The broad pattern of outcomes that might arise in the proposed modelling framework can be demonstrated by considering a simple case that has all the details abstracted out.

The crucial component of the models is the promotion between profession stages, so the natural way to proceed is to suppose that any individual of a discriminated-against gender has to be vastly superior to any rivals of the other gender before being promoted instead of them. That could, for example, arise in practice as a result of applying different (and possibly incorrect) perceived prior probabilities of the abilities for the two genders in conjunction with the actual evidence submitted with the given promotion applications (Heilman 1995; Takács & Squazzoni 2015). The discrimination could also be indirect, rather than direct, for example because one gender is less likely to be awarded prestigious invited talks or prizes (Gürer & Camp 2001), or because the promotion criteria are skewed in favour of one gender (Ginther & Hayes 2003; Mixon & Trevino 2005; Schneider 1998; Williams & Ceci 2015). To allow the clearest possible comparisons with the ability difference simulations, the magnitude of the effect needs to be set to be the same. Thus, the above baseline simulations were re-run with each Gen1 individual only being promoted in preference to a given Gen0 individual in the profession of interest if their ability is at least one standard deviation higher. The existing symmetry across genders is easily maintained in the models by having the discrimination in the opposite direction for the other profession. Then, since this effective ability difference acts in exactly the same way in the models as an actual ability difference, exactly the same stage distributions emerge as seen in Figures 4 and 5 for the ability difference models.

Although the numbers at each stage are exactly the same, an important difference between the discrimination and ability-difference cases is in the average abilities at each stage. A similar pattern emerges for both random profession choice and ability-based choice, though choosing according to ability not surprisingly leads to better ability levels throughout. Figure 10 shows the crucial average ability comparisons for ability-based profession choice. The baseline case (Base) obviously has no effect of gender. In the ability difference case (Dif), the ability of the weaker Gen1 is lower than Gen0 at the initial stage 1, but the ability-based promotions lead to much closer ability levels at the later stages, with both below the baseline level. In the discrimination case (Disc), the Gen0 abilities are reduced to the same extent as in the Dif case, because the reduced competition from Gen1 individuals allows weaker Gen0 individuals to be promoted, while the Gen1 abilities are much higher, due to the extra ability required to achieve promotion. Such higher ability levels for an under-represented gender is another informative signal to look for in real populations. Indeed, similar, though smaller (half a standard deviation), gender differences in ability have been observed in real corporations, suggesting the presence of gender-based discrimination there (Lyness & Heilman 2006). That, of course, does not imply there is necessarily gender-based discrimination or glass ceilings in other cases too, but there is certainly evidence consistent with that existing elsewhere (Sabatier 2010).

Figures 8, 9 and 10 demonstrate how rather different pipeline patterns emerge depending on the situation being modelled. These are just the “pure” cases, with quite large (one standard deviation) differences. In practice, there is likely to be more than one form of discrimination or ability difference present, with varying magnitudes, and untangling the various factors will be more challenging. This is where the modelling approach presented here is likely to prove most useful, as it enables all the possible combinations and variations to be simulated relatively easily and reliably, with the inevitable interactions accommodated automatically.

Intervention Policies

The gender inequalities found in the numbers entering some professions, and the associated shrinking pipelines, are regularly highlighted as being important issues that need addressing. In addition to the natural injustice of any discrimination present, there may be important practical consequences for society as a whole. For example, the noticeable lack of women in certain higher stages of academia might discourage women from studying those subjects, and that may lead to critical skilled-worker shortages in related areas (Camp 1997), or the lack of diversity may worsen team performance (Handelsman et al. 2005; Herring 2009).

How best to address these gender inequalities, or manage other diversity issues, is not clear (Shen et al. 2009). The most direct intervention would be to simply make sure that the numbers of each gender at each stage of each profession are as equal as possible. The use of women-only shortlists in British politics is one controversial example of attempting to do that (Lovenduski & Norris 1989). While this may not be the best approach in practice, investigating what happens in this extreme case will provide useful limits on what might happen with more subtle interventions. It can also be implemented easily by ranking the eligible individuals of each gender separately, and promoting equal numbers of each gender to the next stage to give the required total number of promotions overall. Doing that in the above modelling framework automatically prevents any significant number differences between the baseline, gender-based ability difference, and gender-based discrimination cases.

Equalizing the numbers of each gender at each stage will obviously have consequences for the associated ability levels. The intervention will have no effect on the baseline averages, because the numbers there were already equal. For the discrimination case, the intervention corrects the gender imbalance there, and brings all the ability levels back into line with the baseline. In the ability-difference case, promoting the less able Gen1 individuals when they do not deserve it leads to them having lower than baseline ability levels at the later stages, but the Gen0 individuals are no longer promoted with less than baseline abilities, so they are brought back into line with the baseline. This is another signal to look for in real populations – lower abilities in the higher stages for a gender with equal or lower numbers might indicate that inappropriate number equalization has taken place.

An important practical issue for any profession concerns the overall average abilities of the individuals at each stage in it, irrespective of their gender. The relevant simulation results are shown in Figure 11. The baseline (Base) and baseline with intervention (Base Int) results are identical, since there is no gender imbalance for the intervention to correct, and these exhibit the best average abilities overall. The discrimination (Disc) case has worse abilities, particularly at the later stages, because it unfairly allows weaker Gen0 individuals to be promoted at the expense of more able Gen1 individuals. Intervention in this case (Disc Int) brings all the abilities into line with the baseline, because the discrimination-based imbalance is successfully corrected, and once again the best individuals at each stage are promoted. The ability difference (Dif) case is overall worse than the baseline and discrimination cases, because that corresponds to Gen1 individuals having lower abilities than the base case, which inevitably brings the population averages down. That needs to be interpreted carefully, however, because if the gender difference instead took the form of improved abilities for Gen0 over the baseline, rather than reduced abilities for Gen1, that would lead to improved population averages over the base case. The crucial question is what happens if intervention is applied in a case like this where no discrimination exists? The answer is clear from Figure 11: the overall population performance in this case (Dif Int) is actually made worse, particularly at the higher stages, primarily as a result of forcing the promotion of Gen1 individuals at the expense of more able Gen0 individuals. This highlights the practical importance of understanding the problems before trying to correct them.

Preferences for Professions

One real-life feature missing from the models presented so far is the effect of personal profession or career choices based on underlying gender-specific preferences for particular professions (Lent et al. 1994; Schreuders et al. 2009; Wang & Degol 2014). Preferences of this kind might emerge as a sensible strategy if gender-based ability differences, and/or widespread discriminatory practices, are known or believed to affect success in the available professions, though they can also be driven by a variety of other forces (Cheryan et al. 2017; Lent et al. 1994; Master et al. 2016; Perez-Felkner et al. 2017; Su et al. 2009; Wang & Degol 2014). They can easily be incorporated into the above models as additional factors that are allowed to vary during the course of the simulations.

All the models presented up to now were run for enough simulated years to allow sufficient time for the various population distributions to stabilize, but none of the ability or preference distributions were allowed to evolve or change in other ways from one generation to the next. However, underlying the general modelling framework proposed here is a fairly standard steady-state evolutionary computation approach suitable for simulating all aspects of life history evolution (Bullinaria 2009, 2017). So far, all forms of evolution and learning in it have been “turned off”, but they can easily be turned on again if required to allow any relevant details to evolve by natural selection (Bullinaria 2009) or propagate by social learning (Bullinaria 2017). For some real animal species, factors such as gender-specific abilities and profession preferences (in the form of differing abilities and adoption rates for relevant tasks such as offspring-care, defence and food-provisioning) are known to have become encoded genetically over the course of many generations, and have co-evolved leading to distinct roles for each gender (e.g., Mech 1999). In such cases, it is unlikely that trying to enforce gender equality across all such roles would be a sensible idea. Other species, in particular humans, have evolved the ability for relevant information such as profession preferences to be passed on mimetically via various forms of performance-led social learning or imitation (Bullinaria 2017), and attempts to modify preferences in those cases may be more appropriate. Modelling entire life-spans over many generations, and the co-evolution of gender-based ability differences, social learning and role preferences in various species, including humans, would certainly be an interesting exercise in modelling life history evolution (Bullinaria 2017; Geary 1998; Kenrick & Luce 2000; Wood & Eagly 2002), but that will not be attempted here. From a practical point of view, that is not so important for the purposes of modern human careers as modelling the profession preferences that one can still hope to change within reasonable timescales, assuming such changes can be shown to be beneficial.

There are clearly many different forms the career preferences could take, but one that is independent of the relevant individuals’ abilities, and one that acts to bias their ability-based profession choices, should suffice to illustrate what kinds of outcomes can emerge and how they depend on the type of preference. Then the distinction between evolved and learned preferences also needs to be explored, along with the differences in the timescales associated with the relevant changes in each case. For most current human professions, gender-specific preferences are almost certainly learned rather than innate (Betz & Hackett 1981; Scherer et al.1990), but there may still be innate ability differences surviving from our evolutionary past that might affect our preferences (Halpern 2012; Kimura 2000; Spelke 2005). Moreover, even when there are no innate ability differences, the influence of preferences and stereotyping on the children’s education may lead to ability differences in adults, which can serve to reinforce the preferences and stereotypes (Cheryan et al. 2017; Lane et al. 2012; Master et al. 2016; Van der Heyden et al. 2016). Identifying such cycles, and approaches to improve the outcomes, is one of the key aims of the general simulation approach proposed in this paper.

Ability-independent preferences

The effect of the simplest form of preferences can be modelled by having individuals choose their professions stochastically, rather than according to their abilities, but with particular probabilities. That can be done by introducing a single gender-specific preference parameter p into the above framework, so each individual will enter one profession with probability p, or the other with probability 1-p. The case of p = 0.5 corresponds to the totally random choice of profession that was tested in the models already presented. There are many ways p values different from 0.5 might arise, but the general idea is that low take-ups of particular professions would emerge as a sensible reaction to poor expected progress in that profession, as indicated by performance of members of the given gender in previous generations. Those expectations could take many forms, such as poor perceived abilities in core underlying subjects like mathematics (Perez-Felkner et al. 2017), but the simulations do not require such details to be specified. The simulations would start with the whole initial population having equal preferences for the two professions, and then individuals in later generations either have innate preferences that evolve slowly by the natural selection of successful parents (Bullinaria 2017), or learned preferences that are acquired by some form of direct observation or social interaction with other individuals (Riegle-Crumb & Morton 2017). The speed at which strong preferences emerge will depend on the details of what drives the preferences, but the broad patterns of results are similar. There is an enormous variety of such models that could be implemented, but, to demonstrate what typically emerges, the following sub-sections will just present one evolutionary simulation and one social learning simulation.

Evolved preferences

Evolution by natural selection can be modelled easily and reasonably realistically here using standard evolutionary computation techniques (Engelbrecht 2007). The details were found to affect the speed of evolution, but to have little effect on the eventual outcomes. First, a simple tournament approach is used to select a parent of each gender by having random pairs of individuals compete and choosing the most successful. This can be implemented conveniently in the current framework by selecting the parents from the individuals most recently removed from the population and measuring their success as the highest stage they reached in their career. Then the genotype of each new member of the population is generated from their parents’ genotypes (i.e., set of evolvable parameters) using appropriate crossover and mutation operators. For the preference probabilities, the simplest approach is to have each new individual inherit the corresponding value from their parent of the same gender, with a random “mutation” added from a small range such as [-0.02, 0.02]. The selection pressure, in conjunction with the small random mutations, is sufficient to allow the preferences to drift away from the symmetric 0.5 values in cases where a final position advantage emerges from doing so. The speed of the preference changes can be increased by starting from a more diverse initial population, or by taking the mutations from a larger range, or by selecting parents from more than two replaced individuals, but that does not change the general pattern of results.

There are eighteen distinct cases that need to be considered, each with one of three basic conditions (baseline, gender-based ability difference, and gender-based discrimination), one of three profession choice approaches (by best ability, purely random, and random with emergent preferences), and either involving, or not involving, intervention to equalize the numbers of each gender at each stage. Clearly, all baseline cases, all ability-based and pure random profession choice cases, and all intervention cases, will lead to preference averages that remain at 0.5 because there is nothing to drive natural selection away from that symmetric situation. All those cases were run anyway, to provide a check that no unexpected biases existed in the simulations. If there is no intervention, both the ability-difference and discrimination case preferences shift towards the profession where the greatest success is most likely, while the preferences for the baseline case remain near the expected 0.5, as shown in Figure 12. This provides a simple explanation for the various gender differences observed in the adoption of specific roles by many animal species, though in practice the ability differences will have co-evolved with the preferences.

Socially-learned preferences

For modern human career preferences, it is more likely that they emerge from some form of social learning, rather than the evolution of innate preferences (Riegle-Crumb & Morton 2017). What exactly is “learned” and how that maps onto preferences will generally depend on the specific professions in question, but, independent of those details, it seems likely that repeated success differentials between genders in a given profession will slowly drive the preferences away from 0.5. There are many ways this might work in practice, but one simple version, that is probably not far from reality in many cases, has each new individual start with the preference of a parent or other specific person (that can conveniently be taken in the simulations to be the last removed individual), and then adjust that by a small amount in line with their own socially-acquired estimation of the current performance of their gender. The adjustment would include an increase when the preference does not seem strong enough, and some form of moderation or preference decay to allow the preferences to drift back to 0.5 should the differentials disappear, and to prevent them from becoming stuck at 0 and 1.

Some measures of success, such as the relative numbers of each gender at the highest profession stage, can lead to instability, with small random fluctuations leading the preferences to run away to 0 and 1. Probably more realistic are success measures like the average profession stage achieved by each gender, in which case the starting preference for each new individual would be increased in proportion to the current success difference between genders (with some scale factor η), and decreased in proportion to the difference in preference from 0.5 (with some scale factor λ). These scale factors will act in a similar way to standard neural network learning (η) and regularization (λ) parameters (Engelbrecht 2007), and both will need to be set in line with the particular scenario being modelled. The speed of preference change can easily be increased/decreased by using larger/smaller values of η and λ, and the final preferences will depend on their ratio, subject to floor and ceiling effects. Figure 13 shows how strong preferences consistently emerge from the differences in average profession stage achieved by each gender, in both the ability difference and discrimination cases, for η = 0.1 and λ = 0.1, 0.2, 0.4, but stay near 0.5 when there are no gender differences.

Despite the different underlying driving forces, it is seen that similar patterns of preferences emerge as in the evolutionary simulations of Figure 12, though a lot more quickly. Both the evolution and social learning begin with individuals inheriting their parent’s preferences. The key difference is how those preferences then change. With evolution, they mutate by a random amount in a random direction, and later parent selection leads to the best changes tending to propagate into the future. With social learning, the preferences vary in line with current estimates of what change would be best, which generally leads to faster progress, though that clearly depends on the details of the learning process. Unfortunately, social learning can also propagate ideas that bear no relation to what is actually best, such as stereotypical ideas of what boys or girls should want to do, and simulating that can be done in the same way, but will require a good understanding of what are the driving forces behind those ideas.

Consequences of clear preferences

The emergent preferences, whether from evolution or social learning, make sense, but there remains an important question concerning them. Since the professions and genders are set up symmetrically, and there is a fixed promotion rate at each stage, the overall average position at any given time for each gender must be independent of all the other factors, including any changing profession preferences, so it is not obvious what exactly the preference changes are optimizing. The simulation results provide the same answer independent of what causes the preference changes: Figure 14 shows the average profession stages achieved by one particular gender while the preferences change as shown in Figure 12 due to an ability difference or discrimination providing a promotion advantage for Prof2. The average profession stage achieved by each gender over both professions is constant, as symmetry requires, but the average positions achieved in both professions decrease as a result of the preferences shifting away from being equal. Initially, the average stage achieved in Prof2 is higher than that achieved in Prof1, because that gender is either more able or less discriminated against in Prof2. Then, as particular profession preferences are acquired over time, both genders gravitate towards the profession they tend to do best at, increasing the competition there, and reducing the average position there for their gender. That is why the average stage achieved in Prof2 falls. Meanwhile, those individuals remaining in the other profession then face a larger pool of competitors of the more successful gender, so they are worse off on average too. That is why the average stage achieved in Prof1 falls. It is the increased number of individuals ending up in the “best” profession for their gender that keeps the average position constant throughout. Moving from Prof1 to Prof2 here will improve the outcome for those individuals that switch, but having the majority of individuals do that reduces the average stage reached in both professions for both genders. The resulting constancy of the overall average stage achieved means it cannot be the driving force behind any emergent preferences. It is the individuals with more appropriate preferences doing better that results in strong preferences emerging.

Biased ability-based preferences

The above ability-independent probability-based choices of profession show most clearly how preferences can emerge through evolution or learning, and that form of profession preference will be appropriate when the relevant ability levels for each profession are unknown or difficult to determine. However, real individuals will often have a good idea of their own abilities, and it would be foolish not to take them into account when choosing their profession. The earlier simulations have already shown how simply having each individual make the profession choice that results in them ending up in the profession for which they have best ability is beneficial for the individuals in that it leads to them reaching higher stages in their chosen profession. Moreover, when there is a some kind of gender-based ability difference, that strategy is sufficient to lead to much larger numbers entering the profession their gender generally does best at. However, it seems unlikely that form of pure ability-based profession choice will always be the best strategy. For example, other forms of professional preference may provide better strategies in situations where there is some form of gender-based discrimination. The idea here is that rather than making a pure ability-based choice, or a pure ability-independent probability-based choice, the profession preference takes the form of a bias to the pure ability-based choice, in such a way that if a pure-ability based choice really is best, a zero bias will emerge. In a sense, the bias encodes what can be learned from the past performance of each gender and uses that to enable better profession choices in the future.

A natural way to implement such profession preferences would be to have an evolved or learned bias b that is added to the abilities a_p before an ability-based choice of profession p is made. So profession Prof1 would be chosen if a₁+b/2 > a₂‑b/2, otherwise Prof2 would be chosen.  If Prof1 generally leads to better success for the given gender, b will be positive, and writing the inequality as a₂ – a₁ < b shows that the bias b is essentially a measure of how much better an individual needs to be in their gender’s non-preferred profession for it to be wise to choose it.  Thus, b = 0 corresponds to the earlier pure ability-based choice of profession, and a very large b corresponds to the definite choice of Prof1 encoded as p = 1 in the earlier probability-based approach. If changes to the bias b are driven by gender-specific success differentials in each profession, of the same form underlying the earlier probability-based approach, the bias will act to stop the weakest individuals from entering the profession their gender is least likely to do well at, until equal levels of success are achieved by both genders.

There are two important differences between this approach and the earlier ability-independent preference approach.  First, if a gender-based average success differential has been minimized by learning a non-zero bias b, and the cause of the original differential later disappears, the learned b value will then lead to inappropriate profession choices with resulting success differential in the opposite direction that will cause b to decay automatically back to zero.  That means, unlike for the ability-independent preference probabilities, an explicit decay factor λ for the preference bias is not necessary.  Thus, appropriate biases b can be learned by simply starting each new individual with the b value of their parent or other role model (conveniently taken, as before, to be the last removed individual in the simulation), and incrementing that in proportion to the current success difference between genders (with some scale factor η that again acts as a learning rate).  The second difference is that the involvement of abilities in the profession choice means the learned biases will no longer necessarily be the same in the discrimination and ability difference cases.

Figure 15 shows how profession biases b emerge from the differences in average profession stage achieved by each gender for the baseline, ability difference and discrimination cases for learning rate η = 1.0 and no interventions. The speed of learning here again depends on the various parameter values used, but clear bias-encoded preferences consistently emerge to equalize the average performances of each gender in each situation. The bias stays close to zero for the baseline case, where there are no population-wide ability or discrimination differences to render a personal pure ability-based choice sub-optimal. It ends up around ±1.0 for the ability difference case, where the existence of a better or weaker gender means a small personal ability difference may not be a sufficient indicator of future success. Finally, it takes on larger values around ±2.2 for the discrimination case, where the presence of positive discrimination in one profession and negative discrimination in the other results in an overall underlying effect of two standard deviations beyond the personal ability difference.

Practical Consequences

Often the most important practical issue for the businesses or universities concerned, and society as a whole, is the average abilities at each stage in each profession, irrespective of the relative or absolute performances of the individual genders, or the relative numbers of each gender. This issue will now be explored for the various scenarios modelled so far.

The simulation results presented in Figure 11 already show the relative ability levels for the various ability difference, discrimination and intervention cases for unbiased ability-based profession choice. The important practical issue is how interventions affect the average ability, and hence performance, that emerges for each profession stage. The consequence of interventions to equalize the numbers across genders is an overall ability improvement in cases of gender-based discrimination, since it ensures that the most able individuals get accepted into the profession or promoted within the profession. However, applying the same intervention leads to worse overall performance if the inequality in numbers is actually due to some form of ability differences rather than discrimination, since it allows weaker individuals to be accepted into the profession, or promoted within the profession, at the expense of more able individuals of the other gender.

It seems likely that profession choice preferences exist in many real-world scenarios, and in the most extreme situations, emergent ability-independent preferences can be very strong as seen in Figure 12 and Figure 13. The overall ability levels at each profession stage for the strong evolved preferences of Figure 12 are shown in Figure 16, and similar outcomes emerge for socially learned preferences of similar magnitudes. In these cases, each profession employs individuals almost exclusively of one gender, so the effects of gender-based discrimination or ability differences are very small, and all the ability levels converge, except for the small number of individuals who persist in the profession that discriminates against them. As discussed for the ability-based profession-choice results of Figure 10, the higher abilities of the under-represented gender here provide a clear signal that is worth looking for in real professions as an indicator of discrimination. Moreover, that signal is quite robust, in that it also arises for intermediate cases in which preferences and abilities are combined in various ways to select the profession.

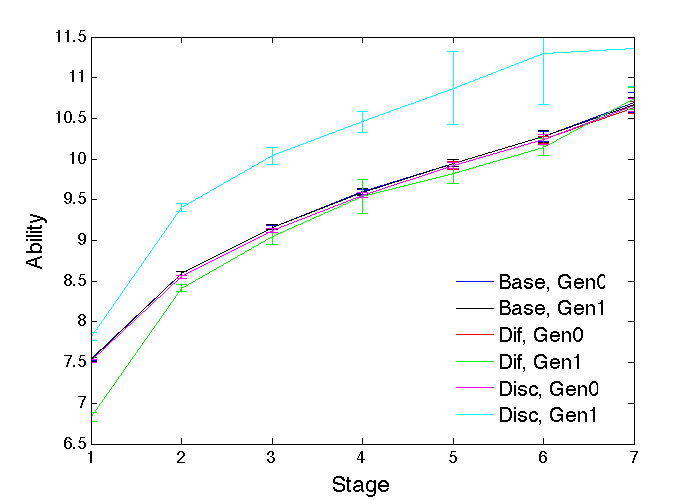
The inevitable question of practical importance here is: how does the emergence of strong profession preferences from success differentials, and the associated gender imbalances across professions, affect the overall ability levels, given that they have been driven purely by individuals wanting to reach higher positions in their chosen profession? The various ability levels for each gender at each stage of their most appropriate profession (i.e., the profession they are most likely to do well in for whatever reason) for the four profession choice approaches discussed above are compared in Figure 17. The best overall abilities arise from ability-based profession choice, and the worst arise from random profession choice. That is not surprising, given how those choices affect the individuals’ capacity to perform to the best of their potential. A less obvious result is that the emergent probability-based ability-independent profession preferences are able to bring the ability levels close to those of ability-based profession choice, particularly at the higher stages. This could be of enormous practical importance for the society as a whole if the relevant abilities are difficult to assess before the profession choices need to be made. For the ability-bias approach to preferences, there is no significant difference in the emergent abilities from pure ability-based choice, apart from at the entry level where they are slightly lower. The practical difference here is an increased proportion of individuals in the profession their gender does best at, 91.3% (std. dev. 0.4%) in the biased-ability case, compared with 77.7% (std. dev. 0.6%) in the pure-ability case, which is highly significant (t test, p < 10^-60).

Another practical question for individual businesses or academic departments, is what should they do if they are confident they have eliminated all forms of discrimination but still find they have a significant gender imbalances. Doing nothing might not be the best option if the intake of one gender is reduced due to issues earlier in the supply chain, or unhelpful preferences persisting from the past, or the actions of other less-enlightened businesses or departments elsewhere, because that will harm their overall ability levels, and do little to improve any inappropriate success-based preferences in the future. However, key to knowing what is best to do is understanding what exactly is happening. Again, a couple of abstract case studies should suffice to illustrate the kind of results that can come out of the models.

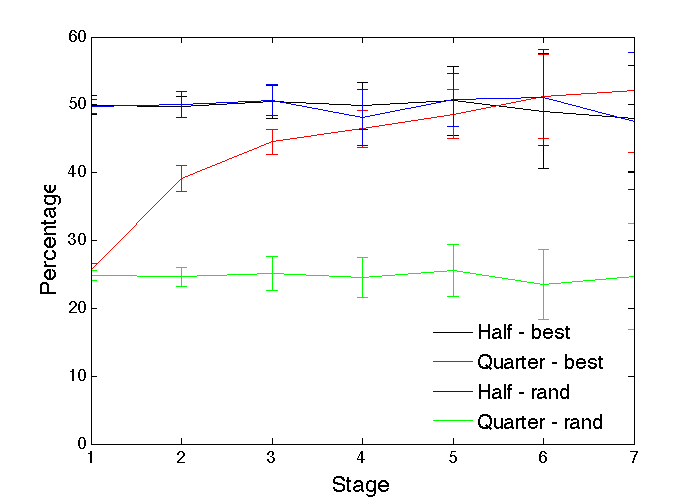
There are clearly many gender-specific factors (such as low perceived potential for success, lack of suitable role models, reduced self-efficacy, and indirect forms of discrimination) that could be underlying the kinds of career preferences discussed in the last section and discouraging particular young people from entering certain professions in the first place, such as women in the field of computer science (Cheryan et al. 2017; Gürer & Camp 2001; Wang & Degol 2014). Fortunately, the consequences of such initial disparities can be modelled without needing to specify exactly what factors are reducing the numbers entering the given profession. The baseline case has equal numbers of each gender entering each professions (i.e., 50%), and that can be compared with the case where each gender has far fewer individuals entering one profession than the other (25% and 75%). If there are no further forms of discrimination present, no ability differences, and totally random choices of profession, those initial differences persist throughout the profession stages as seen in Figure 18. However, if all of the individuals choosing that profession are doing so according to their best abilities, the individuals of the under-represented gender are likely to be at the higher end of their ability distribution, and fair promotions allow them to rise quickly through the stages so that the gender proportions become equalized at the highest stages. These outcomes are in clear contrast to the shrinking pipelines seen in Figure 8 for the case of gender-based ability differences in discrimination-free environments, and provide further signals that can be looked for in real populations to elucidate what is happening.

A related question of practical importance is how quickly can inappropriate profession preferences be reset once they have come into being? The obvious relevance of this is for understanding how any preferences arising from discrimination in the past will change after the discrimination has been successfully eliminated. However, it could also be relevant for situations in which technological or cultural changes have eliminated past gender-based ability differences. If strong preference probabilities have emerged slowly over long evolutionary timescales, like in Figures 12 and 14, it will generally take a similarly long time for them to equalize. If the preferences emerge due to social learning based on differentials in the average stages achieved, as resulted in the preference changes seen in Figure 13, then they will automatically return to 0.5 once the discrimination is eliminated, as seen in Figure 19, with timescales that depend on the details of the processes involved. Similarly, ability-bias preferences of the form seen in Figure 15 will automatically return to zero with timescales similar to their original growth. However, if the preferences are driven by the numbers in the higher stages, rather than average stages achieved, and they are low because of the existing preferences, it will be difficult for them to change automatically, and other measures may be required to equalize the preferences. While this issue can clearly be explored in the models, the simulation results will only be as good as our understanding of what exactly is driving the preferences and the associated timescales, and there is no reason why the social learning cannot be manipulated to speed up the eradication of unhelpful past career preferences.

Discussion and Conclusion

This paper has introduced an agent-based modelling framework that enables the simulation of gender inequalities in any “professions” that involve ability-driven “promotions” up through some form of hierarchy. It is general enough to allow models of gender-specific roles in any species, but has primarily been motivated by a desire to better understand human career progression. A representative series of simulation results based on typical human career structures have been presented to demonstrate how such models lead to reliable results across a number of key simplified scenarios, though the eventual aim is that the approach will be fine-tuned to generate novel results for more realistic real-world scenarios. The models presented have served to establish how the principal factors can be studied effectively within the framework, and illustrated how distinct causes can lead to indistinguishable consequences, how gender-based individual profession preferences can emerge by natural selection or social learning, how applying appropriate interventions can eliminate the effects of discrimination, and how inappropriate interventions can end up making matters worse rather than better.

A key advantage of the models is that they may be used to identify clear signals in the outcomes that can be looked for in real situations to elucidate the underlying causes of any gender inequalities there. For example, some such signals already observed in the simulations presented in this paper are:

1. Differences in the detailed pattern of leaky pipelines of the forms seen in Figures 8 and 9 can signify whether gender-based ability differences are in the means or in the variances.
2. Under-represented genders having higher abilities in the higher career stages, as seen in Figures 10 and 16, is likely to be a sign of discrimination against that gender.
3. Under-represented genders having lower abilities in the higher career stages, as seen in Figure 11, is a sign that inappropriate intervention in favour of that gender may be happening.
4. An initially under-represented gender becoming more equally represented in the higher career stages, as seen in Figure 18, is a sign that inappropriate profession preferences may exist.

It is expected that more specific signals will be identifiable in models more closely tuned to particular real-life professions.

To simplify the analysis and presentation, the scenarios simulated in this paper have been subject to a number of simplifications and approximations. In particular, all the models reported have involved only two professions, and all the gender-based differences have been symmetric across those professions. In reality, of course, there exist many more than two professions, the individual abilities do not neatly align with those professions, and there is a distinct lack of symmetries throughout. There will also usually be more than one organization (e.g., business or university) for each profession, and switching between them is a common feature of real-life career progression. Nevertheless, the proposed modelling framework is general enough to cope easily with such extensions. The results presented in this paper will then serve as the baseline against which more realistic simulations can be compared.

A common problem with such models is that there are far too many potential gender-based effects for it to be possible to simulate all the possible combinations. However, there already exist numerous ideas and hypotheses that could be tested with the approach, and given that there are so many additional factors that could easily be built into the models, it is hoped that the general agent-based simulation approach will become more widely used in the future. The range of issues that could be tested explicitly with it in the future can be illustrated by a few specific examples: The first concerns the idea that gender differences in risk taking might lead to differences in the variance of certain abilities or promotion strategies (Robison-Cox et al. 2007; Schubert 2006), which ties in with evidence that testosterone affects financial risk aversion and career choices (Sapienza et al. 2009). Another relates to the existence of distinct career paths to the highest stages of some professions, with different gender effects for each (Robison-Cox et al. 2007). For situations where individuals’ learning or experience or professional output increase their perceived abilities in line with the number of years in their chosen profession, or at each stage in that profession, it would be interesting to investigate the different age distributions that emerge for each gender at each stage, and explore the effects of related factors such as maternity leave. It would also be straightforward to look at fixing the number of individuals at each profession stage, rather than leaving them to emerge by promoting a fixed fraction of eligible individuals each year, which would lead to simulations more like those of the corporate management study of Robison-Cox, Martell and Emrich (2007) than the merit-based promotions more typical of academia. Further hypotheses that could easily be explored in the models are that one gender tends to be more aggressive about seeking promotion, or quicker to give up waiting for promotion, or more likely to switch between professions or between different organizations within a profession.

There are also several further details, that have previously been explored and optimized in related simulations of life history evolution (Bullinaria 2009, 2017), that could be incorporated relatively easily into the gender-based modelling approach presented here. The simplest of these concern the possibility of allowing abilities and preferences that vary with age, and replacing any parameters fixed at particular values with parameter value distributions or values that can evolve throughout the simulations. It is also an obvious limitation of the human-inspired models presented in this paper, and the variations suggested so far, that they are all restricted to the span of adult careers, and based on the ability levels individuals have on entering those careers at age 20 years. It would clearly be worthwhile and informative to extend the range of the models to cover the whole human life span, from birth, through the various stages of childhood and education, and on through the adult careers stages already modelled. That would allow the modelling of the emergence of any adult ability differences that are culturally acquired, rather than innate, and enable the exploration of potential interventions in the pre-career stages that might lead to better adult outcomes. One could even go as far as having full-scale models of meme-based individual and social learning of the abilities necessary for particular professions and the associated profession preferences, and possibly also introduce finer-grained details like gender-specific timing preferences for all the relevant crucial events, such as seeking promotion, child rearing, retirement, and so on. Finally, it is likely that some researchers will be less interested in human careers, and prefer to use the approach to model gender-specific roles in the life history evolution of other species, including investigation of how the abilities and preferences for particular roles co-evolve.

Hopefully, this short paper has been sufficient to demonstrate how the general agent-based modelling framework proposed can allow all manner of gender-based career progression factors to be explored in a more systematic manner than previously, in which all the assumptions and simplifications are explicit, and the effects quantifiable. It is inevitable that some readers will disagree with the particular assumptions and simplifications employed in the simulations presented here, but these things can easily be varied. The aim is that progress will be made in the future by other researchers seeing the power of this approach and using it themselves to test the consequences of the various assumptions and simplifications, and performing simulations more carefully matched to their own data and beliefs.

References

ALLEN-HERMANSON, S. (2017). Leaky pipeline myths: In search of gender effects on the job market and early career publishing in philosophy. Frontiers in Psychology, 8, 953. [doi:10.3389/fpsyg.2017.00953]

ALTONJI, J. G. & Blank, R. M. (1999). Race and gender in labor market. Handbook of Labor Economics, 3C, 3143-3259.

BARON-COHEN, S. (2004). The Essential Difference. London, UK: Penguin.

BEASLEY, M. A. & Fischer, M. J. (2012). Why they leave: The impact of stereotype threat on the attrition of women and minorities from science, math and engineering majors. Social Psychology of Education, 15, 427-448.

BENBOW, C. P. (1988). Sex differences in mathematical reasoning ability in intellectually talented preadolescents: Their nature, effects, and possible causes. Behavioral and Brain Sciences, 11, 169-183. [doi:10.1017/S0140525X00049244]

BENNETT, C. (2011). Beyond the leaky pipeline: Consolidating understanding and incorporating new research about women's science careers in the UK. Brussels Economic Review, 54, 149-176.

BETZ, N. E. & Hackett, G. (1981). The relationship of career-related self-efficacy expectations to perceived career options in college women and men. Journal of Counseling Psychology, 28, 399-410. [doi:10.1037/0022-0167.28.5.399]

BEYER, S. (2014). Why are women underrepresented in computer science? Gender differences in stereotypes, self-efficacy, values, and interests and predictors of future CS course-taking and grades. Computer Science Education, 24, 153-192.

BLICKENSTAFF, J. C. (2005). Women and science careers: Leaky pipeline or gender filter? Gender and Education, 17, 369-386. [doi:10.1080/09540250500145072]

BROWNE, K. R. (2002). Biology at Work: Rethinking Sexual Equality. New Brunswick, NJ: Rutgers University Press.

BULLINARIA, J. A. (2009). Lifetime learning as a factor in life history evolution. Artificial Life, 15, 389-409. [doi:10.1162/artl.2009.15.3.Bullinaria.010]

BULLINARIA, J. A. (2017). Imitative and direct learning as interacting factors in life history evolution. Artificial Life, 23, 374-405.

CAHILL, L. (2006). Why sex matters for neuroscience. Nature Reviews Neuroscience, 7, 477-484. [doi:10.1038/nrn1909]

CAMP, T. (1997). The incredible shrinking pipeline. Communications of the ACM, 40, 103-110.

CECI, S. J. & Williams, W. M. (2011). Understanding current causes of women’s underrepresentation in science. Proceedings of the National Academy of Sciences, 108, 3157-3162. [doi:10.1073/pnas.1014871108]

CHASE, I. D. (1974). Models of hierarchy formation in animal societies. Behavioral Science, 19, 374-382.

CHERYAN, S., Ziegler, S. A., Montoya, A. K. & Jiang, L. (2017). Why are some STEM fields more gender balanced than others? Psychological Bulletin, 143, 1-35. [doi:10.1037/bul0000052]

DAVISON, H. K. & Burke, M. J. (2000). Sex discrimination in simulated employment contexts: A meta-analytic investigation. Journal of Vocational Behavior, 56, 225-248.

EDMONDS, B. & Moss, S. (2005). From KISS to KIDS – An ‘Anti-simplistic’ Modelling Approach. In: P. Davidsson, B. Logan & K. Takadama (Eds), Multi-Agent and Multi-Agent-Based Simulation (MABS 2004), 130-144. Berlin, Germany: Springer. [doi:10.1007/978-3-540-32243-6_11]

ELSE-QUEST, N. M., Hyde, J. S. & Linn, M. C. (2010). Cross-national patterns of gender differences in mathematics: A meta-analysis. Psychological Bulletin, 136, 103-127.

ENGELBRECHT, A. P. (2007). Computational Intelligence: An Introduction. Sussex, UK: Wiley. [doi:10.1002/9780470512517]

GALÁN, J. M., Izquierdo, L. R., Izquierdo, S. S., Santos, J. I., del Olmo, R., López-Paredes, A. & Edmonds, B. (2009). Errors and artefacts in agent-based modelling. Journal of Artificial Societies and Social Simulation, 12(1) 1: https://www.jasss.org/12/1/1.html.

GEARY, D. C. (1998). Male, Female: The Evolution of Human Sex Differences. Washington, DC: American Psychological Association. [doi:10.1037/10370-000]

GINTHER, D. & Hayes, K. (2003). Gender differences in salary and promotion for faculty in the humanities 1977–1995. Journal of Human Resources, 38, 34-73.

GÜRER, D. & Camp, T. (2001). Investigating the incredible shrinking pipeline for women in computer science. Final Report NSF 9812016.

HALPERN, D. F. (2012). Sex Differences in Cognitive Abilities (4th Edition). New York, NY: Psychology Press.

HALPERN D. F., Benbow, C. P., Geary, D. C., Gur, R. C., Hyde, J. S. & Gernsbacher, M.A. (2007). The science of sex differences in science and mathematics. Psychological Science, 8, 1-51. [doi:10.1111/j.1529-1006.2007.00032.x]

HANDELSMAN, J. et al. (2005). More women in science. Science, 309, 1190-1191.

HEILMAN, M. E. (1995). Sex stereotypes and their effects in the workplace: What we know and what we don't know. Journal of Social Behavior and Personality, 10, 3-26.

HELBING, D. (2010). Quantitative Sociodynamics. Berlin, Germany: Springer.

HERRING, C. (2009). Does diversity pay?: Race, gender, and the business case for diversity. American Sociological Review, 74, 208-224. [doi:10.1177/000312240907400203]

HOBSON, E. A. & DeDeo, S. (2015). Social feedback and the emergence of rank in animal society. PLOS Computational Biology, 11, e1004411.

HUMPHREYS, L. G. (1988). Sex-differences in variability may be more important than sex differences in means. Behavioral and Brain Sciences, 11, 195-196. [doi:10.1017/S0140525X00049402]

HYDE, J. S. & Mertz, J. E. (2009). Gender, culture, and mathematics performance. Proceedings of the National Academy of Sciences, 106, 8801-8807.

KENRICK, D. T. & Luce, C. L. (2000). An evolutionary life-history model of gender differences and similarities. In: T. Eckes & H.M. Trautner (Eds), The Developmental Social Psychology of Gender, 35–63. Mahwah, NJ: Erlbaum.

KIMURA, D. (2000). Sex and Cognition. Cambridge, MA: MIT Press.

LANE, K. A., Goh, J. Z. & Driver-Linn, E. (2012). Implicit science stereotypes mediate the relationship between gender and academic participation. Sex Roles, 66, 220-234. [doi:10.1007/s11199-011-0036-z]

LENT, R. W., Brown, S. D. & Hackett, G. (1994). Toward a unifying social cognitive theory of career and academic interest, choice, and performance. Journal of Vocational Behavior, 45, 79-122.

LOVENDUSKI, J. & Norris, P. (1989). Selecting women candidates: Obstacles to the feminisation of the House of Commons. European Journal of Political Research, 17, 533-562. [doi:10.1111/j.1475-6765.1989.tb00206.x]

LYNESS, K. S. & Heilman, M. E. (2006). When fit is fundamental: Performance evaluations and promotions of upper-level female and male managers. Journal of Applied Psychology, 91, 777-785.

LYNESS, K. S. & Judiesch, M. K. (1999). Are women more likely to be hired or promoted into management positions? Journal of Vocational Behavior, 54, 158-173. [doi:10.1006/jvbe.1998.1646]

MARTELL, R. F., Lane, D. M. & Emrich C. (1996). Male-female differences: A computer simulation. American Psychologist, 51, 157-158.

MASTER, A., Cheryan, S. & Meltzoff, A. N. (2016). Computing whether she belongs: Stereotypes undermine girls’ interest and belonging in computer science. Journal of Educational Psychology, 108, 424-437. [doi:10.1037/edu0000061]

MECH, L. D. (1999). Alpha status, dominance, and division of labor in wolf packs. Canadian Journal of Zoology, 77, 1196-1203.

MILLER, D. I. & Wai, J. (2015). The bachelor’s to Ph.D. STEM pipeline no longer leaks more women than men: A 30-year analysis. Frontiers in Psychology, 6, 1-10. [doi:10.3389/fpsyg.2015.00037]

MIXON, F. & Trevino, L. (2005). Is there gender discrimination in named professorships? An econometric analysis of economics departments in the US South. Applied Economics, 37, 849-854.

MOSS-RACUSIN, C. A., Dovidio, J. F., Brescoll, V. L., Graham, M. J. & Handelsman, J. (2012). Science faculty’s subtle gender biases favor male students. Proceedings of the National Academy of Sciences, 109, 16474-16479. [doi:10.1073/pnas.1211286109]

PEREZ-FELKNER, L., Nix, S. & Thomas, K. (2017). Gendered pathways: How mathematics ability beliefs shape secondary and postsecondary course and degree field choices. Frontiers in Psychology, 8, 386.

RICHIARDI, M., Leombruni, R., Saam, N. & Sonnessa, M. (2006). A common protocol for agent-based social simulation. Journal of Artificial Societies and Social Simulation, 9 (1) 15: https://www.jasss.org/9/1/15.html.

RIEGLE-CRUMB, C. & Morton, K. (2017). Gendered expectations: Examining how peers shape female students’ intent to pursue STEM fields. Frontiers in Psychology, 8, 329.

ROBISON-COX, J. F., Martell, R. F. & Emrich, C. G. (2007). Simulating gender stratification. Journal of Artificial Societies and Social Simulation, 10 (3) 8: https://www.jasss.org/10/3/8.html.

ROSENBAUM, J. E. (1979). Tournament mobility: Career patterns in a corporation. Administrative Science Quarterly, 24, 220-241.

SABATIER, M. (2010). Do female researchers face a glass ceiling in France? A hazard model of promotions. Applied Economics, 42, 2053-2062. [doi:10.1080/00036840701765338]

SAPIENZA, P., Zingales, L. & Maestripieri, D. (2009). Gender differences in financial risk aversion and career choices are affected by testosterone. Proceedings of the National Academy of Sciences, 106, 15268-15273.

SCHERER, R. F., Brodzinski, J. D. & Wiebe, F. A. (1990). Entrepreneur career selection and gender: A socialization approach. Journal of Small Business Management, 28, 37-44.

SCHNEIDER, A. (1998). Why don’t women publish as much as men? Chronicle of Higher Education, 45, 14-16.

SCHREUDERS, P. D., Mannon, S. E. & Rutherford, B. B. (2009). Pipeline or personal preference: Women in engineering. European Journal of Engineering Education, 34, 97-112. [doi:10.1080/03043790902721488]

SCHUBERT, R. (2006). Analyzing and managing risks – On the importance of gender differences in risk attitudes. Managerial Finance, 32, 706-715.

SCZESNY, S., Formanowicz, M. & Moser, F. (2016). Can gender fair language reduce gender stereotyping and discrimination? Frontiers in Psychology, 7, 25. [doi:10.3389/fpsyg.2016.00025]

SHEN, J., Chanda, A., D’Netto, B. & Monga, M. (2009). Managing diversity through human resource management: An international perspective and conceptual framework. International Journal of Human Resource Management, 20, 235–251.

SPELKE, E. S. (2005). Sex differences in intrinsic aptitude for mathematics and science? A critical review. American Psychologist, 60, 950-958. [doi:10.1037/0003-066X.60.9.950]

SU, R., Rounds, J. & Armstrong, P. I. (2009). Men and things, women and people: A meta-analysis of sex differences in interests. Psychological Bulletin, 135, 859-884.

TAKÁCS, K. & Squazzoni, F. (2015). High standards enhance inequality in idealized labor markets. Journal of Artificial Societies and Social Simulation, 18 (4) 2: https://www.jasss.org/18/4/2.html. [doi:10.18564/jasss.2940]

VAN DER HEYDEN, K. M., van Atteveldt, N. M., Huizinga, M. & Jolles, J. (2016). Implicit and explicit gender beliefs in spatial ability: Stronger stereotyping in boys than girls. Frontiers in Psychology, 7, 1114.

WAI, J., Cacchio, M., Putallaz, M. & Makel, M. (2010). Sex differences in the right tail of cognitive abilities: A 30 year examination. Intelligence, 38, 412-423. [doi:10.1016/j.intell.2010.04.006]

WALKER, E. & Rodger, S. (1996). PipeLINK: Connecting women and girls in the computer science pipeline. In: Proceedings of the National Education Computing Conference, 378-384.

WANG, M. T. & Degol, J. (2014). Motivational pathways to STEM career choices: Using expectancy-value perspective to understand individual and gender differences in STEM fields. Developmental Review, 33, 304-340. [doi:10.1016/j.dr.2013.08.001]

WANG, M. T., Eccles, J. S. & Kenny, S. (2013). Not lack of ability but more choice: Individual and gender differences in choice of careers in science, technology, engineering, and mathematics. Psychological Science, 24, 770-775.

WILLIAMS, W. M. & Ceci, S. J. (2015). National hiring experiments reveal 2:1 faculty preference for women on STEM tenure-track. Proceedings of the National Academy of Sciences, 112, 5360-5365. [doi:10.1073/pnas.1418878112]

WOOD, W. & Eagly, A. H. (2002). A cross-cultural analysis of the behavior of women and men: Implications for the origins of sex differences. Psychological Bulletin, 128, 699-727.