"The reciprocal relationship of epistemology and science is of noteworthy kind. They are dependent upon each other. Epistemology without contact with science becomes an empty scheme. Science without epistemology is – insofar as it is thinkable at all – primitive and muddled." Albert Einstein (1949, pp. 683-684)
Introduction
Agent-based simulations have become increasingly prominent in various disciplines. Like many others, I welcome this trend. But with the growth of the field and its growing interdisciplinary nature, the absence of standards in terms of model presentation and interpretation becomes ever more apparent (Lee et al. 2015; Macal 2016; Schulze et al. 2017). While too strict standards would certainly limit the creativity of the research community, some standardization is required to ensure that models can be reasonably compared and related to each other (see also Müller et al. 2014).
Researchers have already responded to the need for standards in various practical ways. With regard to the presentation of agent-based models (ABM), in particular the description of their aim and functioning, Grimm et al. (2006) suggested the ODD protocol, updated in Grimm et al. (2010). The ODD protocol is meant to provide a common format for the description of ABMs and aims to facilitate their mutual relation and replicability[1]. Müller et al. (2013) extended the ODD protocol to facilitate the description of agent decision making. Similarly, the MoHuB framework tries to provide “a tool and common language to describe, compare and communicate” formal models of human interaction, particularly in the context of natural resource management (Schlüter et al. 2017). Another attempt in this direction is the TRACE framework, which was originally suggested in Schmolke et al. (2010) and updated by Grimm et al. (2014). It also seeks to increase the transparency and comparability of simulation models, yet it focuses on the way the functioning of the model is analysed and documented. Finally, the systematic design of experiments (DOE) offers an excellent framework for the study of model behaviour and the presentation of model results in a transparent and comparable manner (Lorscheid et al. 2011).
In this paper I will make a different, yet complementary suggestion to increase the transparency and comparability of computational models: I will not focus on the presentation of ABM and their functioning, but on the ways models are related to reality and thus meant to create knowledge about the system under investigation (SUI). Models always differ from the system they are meant to represent and there are different epistemological ways of relating one’s model to reality[2]. Making differences between distinct epistemological strategies explicit would contribute to better comparability among computational models and thus, the cumulative growth of knowledge in the scientific community.
The process of relating one’s model to reality is related to the intended purpose and model interpretation, and it entails two important activities: model verification and model validation. A great number of different and useful verification and validation techniques exist and the development of new tools is an active and successful area of research (Fagiolo et al. 2007; Rand & Rust 2011; Lorscheid et al. 2011; Lotzmann & Wimmer 2013; Alden et al. 2013; Lee et al. 2015; ten Broeke et al. 2016; Schulze et al. 2017).
However, there are no standards with regard to verification and validation on two distinct and equally important levels. On the more practical level, there is no consensus on the ‘best’ tool for either verification and validation. This is because the complexity, the structure and the purpose of the model at least partly dictate the choice of verification and validation techniques (Sun & Müller 2013; Schulze et al. 2017). There is, however, a lively debate on the adequateness of different tools, and innovative new methods are constantly developed in the ABM community (Lee et al. 2015; Schulze et al. 2017; Schlüter et al. 2017).
On the meta-theoretical level, there is no consensus on questions such as (1) “Is it necessary to verify and/or validate a model?”, (2) “To what extent is the verification and validation of a model even possible?”, or (3) “If model verification and validation are needed, what kind of verification and validation is adequate for the model at hand?” These are epistemological questions and they relate to the deeper problem of how a formal model, an agent-based model in particular, helps us to ‘understand’ a real system under investigation. While being more abstract, epistemological questions are by no means less important than the more practical questions raised above. Nevertheless, they usually receive less attention, which is why they are the main concern of the present paper.
Discussing the coherence of models and their relation to reality is an important activity for every research community and it is essential that these discussions can be carried out effectively. This is exacerbated however, by the fact that different researchers often come with different views on how knowledge can and should be created about the system they investigate. Furthermore, the accepted criteria for what leads to an understanding of, or knowledge about the system under investigation can be very different between various scientific communities (Boero & Squazzoni 2005; Lehtinen & Kuorikoski 2007; Baumgärtner et al. 2008)[3]. Because of this, scholars also understand and value model verification and validation differently.
In overcoming the resulting obstacles to successful cooperation, the analytical apparatus developed by philosophers of science can of great value. Their concepts and vocabulary can be helpful in aligning these different perceptions to each other and, thus, to facilitate the comparison and relation of ABMs and other formal models. Moreover, their analytical language can help to structure the debate about the adequate means for model verification and validation, and might facilitate the dialogue among modellers from different disciplines.
Unfortunately, the literature on applied computational modelling and on the epistemology of modelling remain – so far – largely unconnected. Thus, one goal of this article is to introduce some epistemological concepts that can help applied modellers to carry out discussions about the application, justification and assessment of models more effectively. Alongside important analytical concepts of philosophers of sciences, a particular epistemological framework that may complement applied frameworks such as ODD+D or TRACE will be introduced.
Thereby, the paper does not seek to resolve the philosophical controversy among the nature of models and their relation to reality. Rather, it tries to make accessible some of the philosophical concepts on models to the applied scientists using computational models.
To achieve this we will take the following steps: The next section provides a short and concise review of concepts developed by philosophers of sciences that are helpful for the debate in the simulation community. These ideas will be summarized in a framework that helps clarifying the different strategies to give models epistemic meaningfulness. Then we will relate model verification and validation to this framework, describe the meta-theoretical relation between verification and validation, and discuss whether and when models should be verified and/or validated. In a subsequent step, we identify some immediate practical implications from the epistemological discussion above. Finally, we conclude the paper and summarize the implications for future research.
How Models Generate Knowledge about Reality
This section introduces some of the key vocabulary and essential concepts developed by philosophers of science that are concerned with the question of how models create knowledge. Then it outlines a framework that accommodates these concepts in a way that is appealing to practising modellers. Initially however, the usefulness of referring to epistemology and the philosophy of science will be discussed.
The merits of an epistemological perspective on modelling
Epistemology is “the study of knowledge and justified belief” (Steup 2016). In this field of philosophy one asks questions such as “What are the necessary and sufficient conditions of knowledge?”, “What are the sources of knowledge?” or “How can we generate knowledge about the real world?”. Here I will present a couple of reasons for why epistemological reasoning is important for applied scholars and comment on them one by one:
- Epistemological arguments are important when choosing and justifying one’s modelling framework.
- Epistemological reasoning is indispensable for relating results from different models to each other.
- It helps identifying advantages and disadvantages of different modelling frameworks and suggests practical ways for combining them.
- By dealing explicitly with an epistemological framework modellers can reflect upon and improve their own practices.
- An epistemological framework can highlight trade-offs between various modelling desiderata and enables modellers to make more substantiated design choices.
- An epistemological framework clarifies (1) the epistemic content of the sometimes vaguely used concepts of model validation and verification, (2) why and when validation and verification is is important, and (3) what we can expect from it.
If asked why one is approaching a given research question with an agent-based model, the usual answers are of the kind “I want to study the role of the particular interaction structure, and in another modelling framework it is difficult to include this structure explicitly.” or “The heterogeneity of the actors can be represented very directly in an ABM, and this is important for my research question!”. These answers refer to particular epistemological statements because they formulate certain preconditions that must be satisfied by a model to be suitable to answer the research question of the modeller. Here, the implicit epistemological claim is that there are certain properties of the system under investigation that must be represented in the model for the model to be useful.
Such implicit epistemological claims are often discipline-specific and, if not made explicit, a potential obstacle for interdisciplinary work. Economists, for instance, cherish properties that might receive less priority in other social sciences (Lehtinen & Kuorikoski 2007; Cartwright 2010; Reiss 2011). Rodrik et al. (2004, p. 133), for example, claim that “Historians and many social scientists prefer nuanced, layered explanations where these factors interact with human choices and many other not-so-simple twists and turns of fate. But economists like parsimony.” This suggests that economists pay less attention to the realistic-ness of particular modelling assumptions, but focus rather on clarity and simplicity of models[4]. To elucidate such epistemological differences (and to critically assess them from all viewpoints) is essential when we want to engage in interdisciplinary collaboration, and taking an epistemological perspective can help us to do so (Grüne-Yanoff 2013).
More generally, engaging with an explicit epistemological framework can help researchers to reflect upon their actual modelling practices since it requires them to be very precise and explicit on how their model is expected to improve understanding of the target system. Additionally, epistemological frameworks can highlight trade-off among different modelling desiderata, such as transparency, generality, or precision. Thereby, they can help us in making more explicit and grounded design choices, and, in the end, to improve upon our established modelling practices. The identification of trade-offs might also suggest ways in which we can complement our model with other (model-based or non-model-based) perspectives on the target system, which might help remedying the inevitable shortcomings of our model.
Epistemological reasoning can also help us relating results obtained from different methods to each other. For example, there is currently a debate among policy makers and economists on the potential welfare and job effects of a free trade and investment agreement between the European Union and the United States. Francois et al. (2013) - and many others - have tackled this question with a Computable General Equilibrium (CGE) model, the current standard in economic research practice. The authors conclude that the agreement would lead to generally favourable results. Capaldo (2014) uses a conventional macroeconomic model to study the same question but expects job and welfare losses for Europe. Which model is ’better‘, or, which conclusion should form the basis for the decision making of policy makers? Some might argue that the assumptions of Capaldo (2014) are more adequate than those of Francois et al. (2013). Others might trust more in the CGE model because it relies on economic equilibrium, it is easier and thus more transparent and parsimonious. To trace different sources for distinctive policy implications, and to prioritize models in terms of the insights they create, we again need to refer to the epistemological questions posed before. Using explicit frameworks and precise language facilitates this task.
The previous argument relates to a more general finding: different modelling frameworks have respective advantages and disadvantages that are not explicitly reflected upon in disciplinary practice. Taking an epistemological perspective can help to highlight them (Grüne-Yanoff 2013). For example, agent-based economic models are - generally speaking - quite flexible in their assumptions. General equilibrium models[5] are - again, generally speaking - more parsimonious and often allow for analytical solutions. Choosing the right modelling framework and the right model requires a reflection of their strengths and weaknesses. Sometimes, there is no ‘right’ model at all and it makes sense to use multiple models and look at the system under investigation from different angles (Aydinonat 2017). In any case, carrying out a balanced choice of methods and a successful model triangulation is particularly important in the context of interdisciplinary work and again, requires epistemological reasoning (Grüne-Yanoff 2013).
Researchers in the simulation community are often concerned with the problem of choosing the right set of methods for model verification and validation. But the question of when and why verification and validation is important, and how this relates to the purpose of modelling, receives less attention. To argue why a particular method for model validation is important means to make a statement on how the link between the model and reality should be assessed. This, as any other argument made in this context, is an epistemological argument.
In all, there are a number of arguments for why epistemology is important. In contrast to the discussion of the adequate means for model verification and validation, the most important point about epistemological arguments is that they are made explicit. Using an explicit framework helps us to compare models because the way they are meant to explain becomes more explicit, transparent, and, thus, comparable.
Models and reality: A short review of key concepts
The aim of this section is to introduce applied modellers to some of the key concepts developed by philosophers of science. The merit of these concepts is that they allow us to be more precise about how our models can be used to create knowledge about reality. Of course, the philosophical literature on the epistemology of models is extensive and it is beyond the scope of this article to provide an exhaustive review. Rather, I will attempt to provide a concise overview over some of the key concepts introduced by philosophers of science that are particularly useful for the topic of this paper and that can help applied modellers. For a more extensive review from a philosophy of science perspective see e.g., Grüne-Yanoff (2013).
Before we begin, the scope of this review needs to be clarified. First, there is an extensive body of literature concerned with the ontological nature of models, i.e., the question: “What are models?”. There are many suggestions in the literature, ranging from the idea of models as mathematical objects to the idea of models as fiction. For the present discussion the question on the ontology of models is of secondary importance since all the arguments below are compatible with most prominent conceptions. For a review of the relevant literature see e.g., Gelfert (2017).
Second, there is a literature on the function of models (see e.g., Morgan & Morrison 1999; Peschard 2011 or Gelfert 2016 for initial overviews). In the following, I will focus on contributions that treat models as representations of a target system that are geared towards a better understanding of this target. There are other purposes for models, such as entertainment, measurement or further model-construction, but here I focus on models that are used to represent and understand certain target systems in the real world.
Third, whenever we wish to represent and explain a target system there are alternatives to models. As argued in Weisberg (2007), the distinctive feature of modelling is that the system under investigation is studied indirectly: we build a model, we analyse the model, and then we relate the model to reality. An alternative procedure, abstract direct representation, lacks the intermediate step of building a model as a surrogate of the system under investigation: here one describes and studies the target system directly. Yet, for the purpose of this paper, we will be confined to models as means to represent and study reality.
Key vocabulary
I will now start introducing some basic vocabulary used by philosophers of science. This not only helps applied researchers to specify their meta-theoretical considerations more precisely, it also helps them in accessing the epistemological literature more easily. For a summary of all concepts see Table 1.
First, models that serve as representations necessarily have a target, i.e., the system that the model is meant to represent. The target system does not need to be one particular, or even a real system. Schelling’s segregation model, for example, is usually not meant to represent one particular city, but an abstract city such that the argument applies in many instances. We call such targets generalized targets (see e.g. Weisberg 2013, p. 114). Other models are meant to represent targets that do not, or even cannot, exist (so called hypothetical targets, see e.g., Weisberg 2013, p. 121). For example, there are models in computational biology that represent populations of three-sex species, something that has never been found in reality. Yet by showing that a three-sex population comes with enormous costs, such models provide a potential explanation for why there are no three-sex populations in reality (Fisher 1930; Weisberg 2007).
Second, although we do not want to concern ourselves too much with the ontology of models, it makes sense to distinguish three different kinds of structure that can serve as models (Weisberg 2013), sometimes referred as the \(O\)-objects, which provide for the ‘material’ of which the model is built. The first kind are physical models such as the San Francisco Bay model (Army Corps of Engineers 1981) or the Monetary National Income Analogue Computer MONIAC, a hydraulic model of the economy (Bissell 2007). Such models are not very common in the social sciences and will not be the subject of our following considerations. Second, mathematical models are mathematical structures such as functions and state spaces. They are very common in the social sciences. Third, computational models are sets of procedures.
One might well argue that computational models are in fact a subset of mathematical models because the procedures can be described mathematically (Epstein 2006). A similar point is made by philosophers who argue that computational models do not pose any specific philosophical problems and can be treated with the same tools as mathematical models (Frigg & Reiss 2008). The main argument of treating them as a separate category is pragmatic and refers to their different use: the way in which results are derived differs (Lehtinen & Kuorikoski 2007, p. 310) and – because they usually do not allow for analytical proofs – involves a certain “epistemic opaqueness” with regard to the precise derivation of the results (Humphreys 2009). Also, computational models are often generative (Epstein 2006): in contrast to most mathematical models, they generatively ‘grow’ their results from the initial conditions, thereby automatically suggesting concrete mechanisms on how the model results could come about in the target.
This distinction of modelling categories relates to the concept of representational capacities of structures: not all structures can be used to represent any system because some structures are too rigid and not expressive enough. Here, philosophers distinguish between (1) dynamical sufficiency and (2) mechanistic adequacy. These concepts are useful if one wishes to justify the choice of the modelling framework one is using. ‘Dynamical sufficiency’ refers to a model’s capacity to reproduce patterns observed in the target, ‘mechanistic adequacy’ refers to its capacity to represent the mechanistic structure of the target. If we consider the claim that agent-based models are preferable to DSGE models because (1) it is easier to consider the direct interaction of heterogeneous economic agents in these models, and, (2) they produce better predictions, then (1) means that ABM are superior to DSGE models in terms of their mechanistic adequacy, and (2) refers to their alleged superior dynamical sufficiency.
Many philosophers of science make the distinction between models and model descriptions (see e.g., Weisberg 2013, ch. 3)[6]. As indicated above, we consider models to be mathematical structures or sets of procedures. It is important to distinguish between these models and their descriptions (Giere 1990; Weisberg 2013). The descriptions can consist of equations, computer code, pseudo-code, graphs, pictures and most importantly, words. The relation between models and model descriptions is many-to-many: the same model can be described in very different ways. Schelling’s segregation model, for instance, can be described via source code, equations, or words, among others. Yet at the same time, descriptions usually do not describe a model in every detail and some aspects are frequently omitted. Thus, the same description often specifies different models, and the less precise the description, the more models it can specify. In the following we focus on models, rather than on their descriptions.
Many modern accounts argue that models are not representations by their very nature, but that they are made representations by the explicit stipulation of the modeller (Peschard 2011, p. 337). In effect, this implies that “models do not have a single, automatically determinable relationship to the world” (Weisberg 2007, p. 218), but that model users have to specify how they intend to use a model. These intentions underlying any model are summarized as the construal of researchers and include the assignment (or ‘denotation’) and the intended scope of the model.
| Term/Concept | Description |
| Target of a model | The real or fictional system/object that a model intends to represent. There are particular, general or hypothetical targets. |
| \(O\)-object | The fundamental structure (or ‘material’) of the model, determines the type of the model. |
| Type of model | Weisberg (2013) suggests there are three types, depending on the kind of \(O1\)-object used to construct the model: physical models (consisting of matter), mathematical models (consisting of mathematical objects) and computational models (consisting of procedures). |
| Representational capacity | The degree of ‘expressiveness’ of the structure of a model, i.e., its ability to represent a target in line with the fidelity criteria provided by the user. |
| Fidelity criteria | The standards used by the model user to evaluate the ability of a model to represent its target. Can be divided into at least dynamic and representational fidelity criteria. |
| Dynamic fidelity criteria | The desired degree of similarity between the model output and the target, often specified as acceptable error bands. |
| Dynamic sufficiency | The degree of structural sophistication a model must have to produce an output reasonably similar to that of its target, i.e., as similar as articulated in the dynamic fidelity criteria. |
| Representational fidelity criteria | The standards used by the modeller to evaluate the ability of a model to represent the causal structure/mechanisms of the target. |
| Mechanistic adequacy | The degree of structural sophistication a model must have to mimic the causal of its target adequately, i.e., as close as articulated in the representational fidelity criteria. |
| Model description | The description of the model is different to the model itself. The relationship between models and descriptions is many-to-many. |
| Scope | Clarification of what features of the target the model intends to represent. |
| Assignment | Clarification of which part in the model corresponds to (or ‘denotes’) which part in the target, and which parts of the model are to be ignored. |
| Denotation | A binary relation between a model and a target; established via the stipulation of the model user to use the model as a representation of the target. |
| Full explanation | Description of why a certain fact occurred at a particular time in a particular way. Requires the description of all the causal factors that have produced the fact. |
| Partial explanation | Description of the role of some explanatory factors underlying the occurrence of a fact. Involves idealization since not all causal factors were considered. |
| Potential explanation | Description of the factors that could have produced a certain fact. Not confined to actual targets; occurs frequently when general, hypothetical, or theoretical targets are concerned. |
| Exemplified properties | The relevant properties a models exemplifies under a given interpretation. |
| Model key | A dictionary explaining to what properties in the denoted target the exemplified model properties shall correspond. |
| Imputed properties | The properties that the model (truly or falsely) imputes on its denoted target. |
| Mental model | The perception of the researcher of her subject of investigation; also contains her Weltanschaung or ‘pre-analytic Visions’. |
The assignment – or the ‘denotation’ – of a model specifies which part of the model should be mapped on which part of the target (Weisberg 2013, pp. 39-40). Let us consider a macroeconomic model consisting of a few representative agents as an example. One of the agents is called ‘representative household’ and it should represent households in the real world. Another agent is called ‘representative firm’ and it should represent firms. Thus, in total the assignment of the model specifies which target system is actually meant to be represented by the model as a whole.
The intended scope also refers to the coordination of the model and its target: it specifies which particular parts of the target should be represented by the model (Weisberg 2013, p. 40). For example, the intended scope of the original Lotka-Volterra model was the relationship between the abundance of predators and prey. Many aspects of the relationship between predators and prey that are outside the intended scope of the model, such as the spatial distribution of predator and prey populations. Correspondingly, spatial relationships are not modelled explicitly, so the model would imply that the spatial distribution of the populations has no effect – a more than questionable statement. By making the intended scope of the model explicit, i.e., to clarify explicitly that the model is not meant to consider the role of spatial relationships, one makes sure that models are not used for – or judged on the basis of – questions and applications they were not designed for (and for which they might not be well suited).
As emphasized above, different disciplines usually understand ‘explanation’ differently (Lehtinen & Kuorikoski 2007). Yet there are some broad categories of explanation that might be useful to distinguish (Grüne-Yanoff 2010, pp. 37-43):
- Full explanation: A full explanation, also known as ‘how-actual explanation’ shows how a concrete phenomenon has occurred. This entails to describe in detail the causal history preceding the concrete phenomenon and to identify all the relevant causal mechanisms involved. Outside the natural sciences such explanations are very rare.
- Partial explanation: In the case of partial explanations the model isolates some factors deemed important and idealizes away from others. Thus, one explicitly does not include all relevant factors in the model (which is impossible for more complex systems anyway). Although partial explanations are much easier to reach than full explanations, in most applied and social sciences it is still almost impossible to show that a certain model provides for a partial explanation since one can never be sure to have included all the relevant factors.
- Potential explanation: The most common type of explanation in the context of computational models are potential explanations, also known as how-possible explanations. A potential explanation provides a model that represents mechanisms that could in principle have brought about the phenomenon of interest. The Schelling model, for example, provides a how-possible explanation for segregation in a city (Ylikoski & Aydinonat 2014). We do not know whether the underlying mechanisms have actually brought about segregation, but the model shows that they could possibly have brought about segregation[7]. In contrast to full or partial explanations, how-possible explanations are not necessarily directed towards concrete events that have happened in reality, but might also refer to generalized targets (such as ‘segregation’) or theoretical models themselves (e.g., cellular automata), or they might simply illustrate the functioning of purely theoretical mechanisms (Weisberg 2013; Ylikoski & Aydinonat 2014).
Finally, there are several answers to the question “What makes a model an epistemic representation of a target?”, i.e., what are the features of models in virtue of which they represent their target? Here, I will focus on a particular account of models that answers this question, and is appealing for several other philosophical arguments: the so called DEKI account as developed in Nguyen (2016) and as introduced by Frigg & Nguyen (2016)[8].
When is a model a representation of a target? The DEKI account of modelling
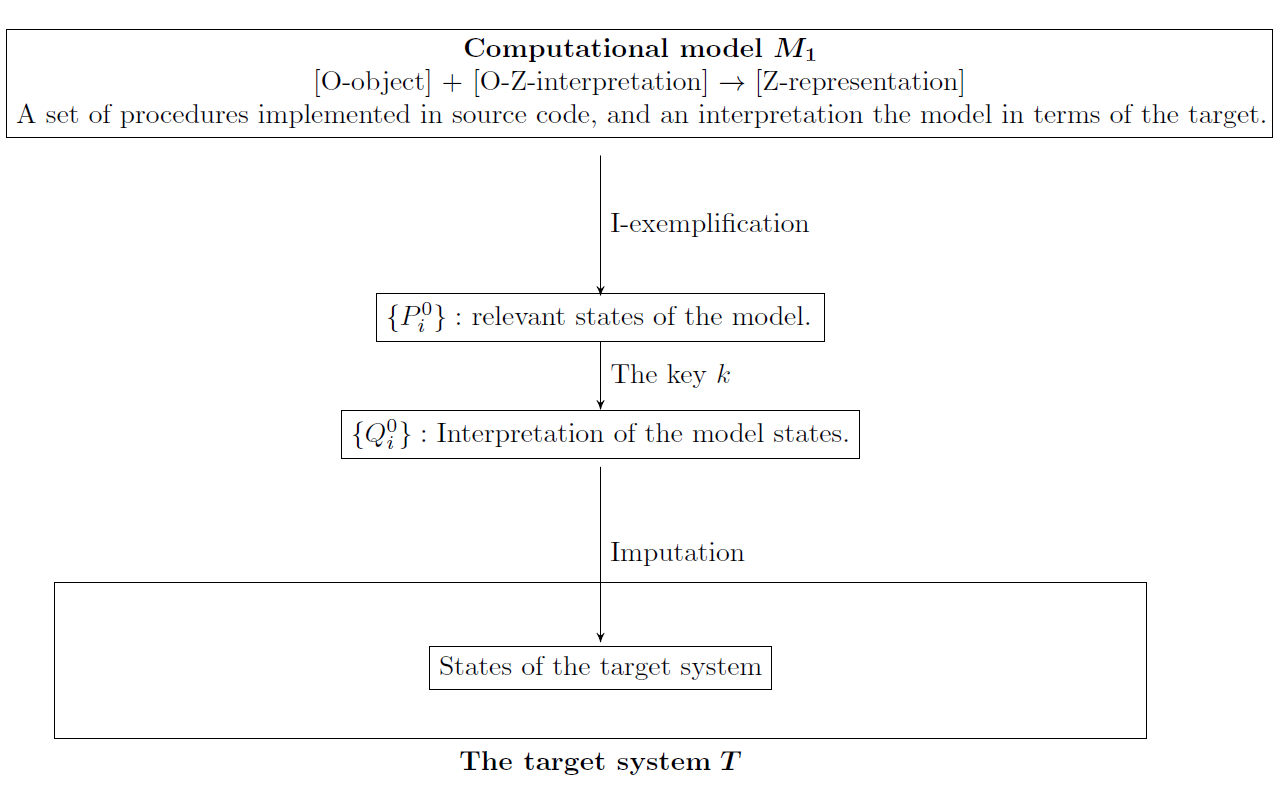
The DEKI account as introduced by Frigg & Nguyen (2016) starts with the notion of a model \(M\) and a target \(T\) and then formulates demands this model must satisfy to count as a representation of \(T\) (the following elaborations will be summarized in Figure 1). A model within the DEKI framework is a certain structure or object, commonly referred to as an \(O\)-object. As argued above, we will not delve deeper into the ontological status of models. For us, the \(O\)-object corresponds to the type of model and is thus a set of mathematical objects (for the case of mathematical model) or a set of procedures (for the case of computational models). To count as a model however, the \(O\)-object must come with a certain interpretation that is to be supplied by the model user. We have already specified two important aspects of the interpretation above: the assignment and the intended scope.
Such an interpretation makes the initial \(O\)-object to count as a \(Z\)-representation. A \(Z\)-representation is a one-place predicate and \(Z\) is a place-holder for the kind of the target of the model. For example, a picture \(p\) of a woman is a woman-representation: \(WOMREP(p)\). This does not necessarily mean that it represents one particular woman, it could well be a fictional woman. This is important since some models represent general (such as cities in general instead of a particular city) or hypothetical (such as a three-sex population) targets. As an example, consider a computational agent-based model that is meant to represent a national economy. If this interpretation is explicit we could state \(MACROECON(c)\), where \(c\) stands for a set of algorithms and \(MACROECON(c)\) reads as: the set of algorithms \(c\) is interpreted as a macroeconomy-representation. Why do I not say ‘representation of a macroeconomy?’ Because this could wrongly be interpreted in the sense that \(c\) is meant to represent one particular macroeconomy. We want to be less restrictive in our claims and only say that \(c\) is interpreted (and thus stipulated) as a macroeconomy-representation.
Now that we have clarified the notion of a model \(M\) as an \(O\)-object accompanied by an interpretation that turns it into a \(Z\)-representation, we can specify the four demands that the model must meet to count as a representation of its target \(T\):
- The model \(M\) must denote its target \(T\).
- The model \(M\) must be a \(Z\)-representation exemplifying properties \(P_1,...,P_n\).
- The model \(M\) must come with a key \(K\) that indicates how the properties \(P_1,...,P_n\) can be translated into a set of features \(Q_1,..., Q_m\).
- The model \(M\) must impute some features on its target \(T\) .
The first demand is straightforward: a model user must make clear that he uses the model to represent a target, and she must specify the target the model is meant to represent. The crucial point here is that the model user must make clear that he uses the model as a representation of a target. This is important since a set of algorithms constituting the Schelling segregation model does not by its nature represent segregated cities. Only if the model user makes it explicit that she uses this set of algorithms to represent a city, the set of algorithms becomes a model of a city.
The second demand requires that the \(Z\)-representation must exemplify certain properties \(P_1,...,P_n\). Exemplification refers to the instantiation of a certain property, \(P\), by directly referring to this property. Instantiation must not be interpreted literally, which is why the accompanying interpretation of a model is so important: no agent in an agent-based macroeconomic model literally has some wealth. Rather, we interpret the model such that the agents in the model instantiate properties such as wealthiness. For a smooth and transparent use of a model, it is important that these interpretations are carried out as explicitly and clearly as possible.
The third step is to link the properties of the model, \(P\), to the relevant properties of the target system, \(Q\). How to translate the properties exemplified by the model, \(P\), to the properties of the target, \(Q\), must be specified by a key (or a ‘dictionary’). The simplest example for a key is the legend of a map: it explains how certain points on the map should be interpreted in the area represented by the map. For instance, a big red dot represents a capital, and 1 cm of a black line represents 1000 km of a small road.
Finally, at least one property \(Q\) must be imputed to the target system. Which properties are imputed depends on the intended scope of the model. Such imputations can be false: a model can make a prediction about how the target behaves, but it behaves differently. A model that makes false predictions about its target does not stop representing this target, and imputing properties on the target - it just misrepresents the target because it imputes the properties wrongly on the target.
Let us summarize what has been said about the DEKI account so far in Figure 1: we start with an \(O\)-object, which can be a set of algorithms. We supply an interpretation according to which the \(O\)-object is a \(Z\)-representation, for example an economy-representation. We make clear that the model denotes the target economy. Also, the model I-exemplifies certain properties \(P_1,...P_n\), e.g. a certain wealth distribution of the software agents (this means it exemplifies them under the interpretation I). We supply a key that maps the properties of the models to the properties of the target economy \(Q_1,...,Q_m\). We then impute the resulting properties \(Q_1,...,Q_m\) on the target economy. This can lead to true or false statements, depending on whether the imputed properties correspond in their values to the properties of the target.
A big merit of the DEKI account of Frigg & Nguyen (2016) is that it helps us understand how both very idealized and general models, such as the Schelling model, and very complex and applied models, such as the disease model of Eubank et al. (2004), serve as representations.
Adding details: Dynamics, mental and conceptual models
We now want to add some more specificity to the framework sketched in Figure 1. There are at least three aspects of the model building process that are still missing from Figure 1: the time dimension of models and their targets, the mental models of the researchers, and the conceptual model, which is to be distinguished from the final computational model.
First, many computational models are dynamic models and they are related to their target over time. The current visualization of the DEKI framework does not consider this. To avoid misunderstandings I will adjust the figure so that the model exemplifies potentially different properties at different points of time.
Second, the current visualization does not consider the mental models of the researchers. With mental models I refer to the representation of reality we construct in our brains. Since reality is too complex to be perceived in its entirety, we need to reduce its complexity by abstracting from details, thus building a coarse-grained representation of reality that our mind can process. Cognitive scientists refer to these representations as ‘mental models’ (Johnson-Laird 2005). The basic idea has been nicely summarized already by Forrester (1971):
"Every person in his private life and in his business life instinctively uses models for decision making. The mental image of the world around you which you carry in your head is a model. One does not have a city or a government or a country in his head. He has only selected concepts, and relationships between them, and uses those to represent the real system” (Forrester 1971, p. 112).
Although mental models are distinct from the models we build within the scientific discourse, they do play a role in the construction of scientific models. Considering them in our framework helps us to explicitly accommodate the Weltanschauungen of the researchers which, at least to some extent, always impact our scientific practice (see already Weber 1922): “no model could claim absolute objectivity as each is also subject to the modeller’s subjectivity, view and understanding of the world, and proneness to mistakes” (Augusiak et al. 2014, p. 119). Considering mental models explicitly in our framework highlights this important aspect[9]. Note that the relationship between mental and computational models is not a relationship of representation. A mental model does not represent a computational model or vice versa. Rather, a mental model always implicitly pre-dates a computational model since it allows us to perceive and cognitively process information about the target.
The final – and most important – addition to Figure 1 that is necessary in the context of computational models is that of a conceptual model[10]. The conceptual model is the intermediate model that is created before one implements a computational version of it (Augusiak et al. 2014). It summarizes the aspects of the target considered to be relevant and important for the final computational model. Thereby, it also is a representation of the target, although a much cruder one than the computational model. In practice, the people building the conceptual model are not necessarily the same that build the computational model: a research group might consist of theorists and programmers, with the former designing the conceptual model, which is then implemented by the programmers. For our purposes, it is useful to put the conceptual model into our visualization since it will later help us to accommodate model verification and validation in this figure. Again, there is no relationship of representation between the conceptual and the computational model. Rather, both of them represent the target, and the computational model is a computational implementation of the conceptual model. Alternatively, we can think of the conceptual model as a coarse-grained description of the computational model.
Taking stock
Integrating all the previous considerations into Figure 1 results in the more complex but complete Figure 2. The concepts introduced so far are summarized in Table 1.
For most practical applications, Figure 2 is over-loaded and contains too much details. This is why we will reduce it for the further discussion of verification and validation (see Figure 3a). Also, for applied researchers describing their model using all the concepts introduced in Table 1 would probably be too much of an issue. Therefore, one might use a form as the one in Figure 3b, which could be provided with the model description as an appendix, similar to the ODD protocol.
Aligning Model Verification and Validation within the Epistemological Framework
The epistemological framework introduced above allows us to be precise about the role of verification and validation in the modelling process. While some authors have suggested dismissing the terms because of their ambiguous and careless use in the literature (see e.g., Augusiak et al. 2014; Schulze et al. 2017), I believe that precisely defined, they can highlight two important aspects of model evaluation, which are both important, but conceptually distinct. For the sake of transparency, I relate my terminology to that of Augusiak et al. (2014) in the appendix of this paper. There, the value-added of the terms ‘verification’ and ‘validation’, which will now be clarified, is explained in more detail[11].
With verification I refer to the act of testing whether the model does what it is supposed to be doing, i.e. whether it adequately implements the conceptual model and whether it is free of bugs or other implications not intended by the modeller. The verification of a model takes place after the model has been built (and possibly during the model building process) and should precede any application and/or validation of the model.
Verification usually involves two steps: (1) study what the model is doing, and (2) compare this to what the model is supposed be doing. The first step is often referred to as model exploration. The second step can be carried out in a twofold sense: first, one scrutinizes whether the model does what the programmer wants the model to do. Such scrutiny is mostly concerned with identifying bugs and programming errors. Second, one investigates whether the model adequately implements the underlying conceptual model. This is usually more demanding. In case the people programming the model differ from the people setting up the conceptual model, this step necessarily involves a group effort where the programmers explain the functioning of the model and the theorists (or other stakeholders involved in the model design) assess the adequacy of the implementation. It is worth noting again that both activities are only concerned with the computational and the conceptual model. The target system has not yet a role to play.
Consequently, sensitivity analysis would also be considered some form of model verification since it exclusively aims at understanding the behaviour of the model. For more details see e.g. Beck (2002), or Rand & Rust (2011) for a nice summary and ten Broeke et al. (2016) for a review of different tools for sensitivity analysis[12].
The best method for model exploration is mathematical proof that certain inputs produce a particular output. For computational models, proofs are usually not a viable option and numerical experiments using a computer are required. The resulting “epistemic opaqueness” (Humphreys 2009) is one reason why we have followed Weisberg (2013) in distinguishing between mathematical and computational models, although the distinction collapses on an abstract level (Epstein 2006).
Model validation means to test whether the model is actually a reasonable representation of the target (Rand & Rust 2011, p. 187). Because ‘reasonable’ can have different meanings, there are different forms of model validation to be discussed below. The correct choice depends on the purpose of the model, the desired mechanistic adequacy and dynamic sufficiency, and the imputed properties of the model. However, all forms of validation are distinguished from verification by the fact that they are concerned with the relationship between the model and the target of the model.
We will now align model verification and validation within the framework developed above. As indicated in Figure 4a, model verification is concerned with the internal consistency of the computational model and its fit to the underlying conceptual model. Examples of methods that are used to verify models are unit testing (i.e. explicit tests for important aspects of the code, e.g. via assertions), code walkthroughs (i.e. an explicit description of what every line of code does), degeneracy testing (i.e., testing whether the code produces the desired output for extreme values of input), or the implementation tools ensuring the traceability of model outcomes (i.e. a clarification of how each step in the model relates to previous steps and design decisions; see e.g., Scherer et al. 2015 for a description and an illustration for the case of large-scale policy models).
Considering these methods and keeping in mind that often “confirming that the model was correctly programmed was substantially more work than programming the model in the first place” (Axelrod 1997) we might want to keep the effort needed for verification at a minimum and thus ask the question: “What can we do to make model verification easy?” Firstly, we should build simple models. The simpler the model, the easier verification (ten Broeke et al. 2016). This is obvious since the simpler the model, the fewer variables and mechanisms one has to check. In the best case, the model is in a form that makes it even amendable for analytical proofs.
Secondly, we should build transparent models. There are a number of tools developed in the simulation community to increase model transparency: the systematic DOE (Lorscheid et al. 2011) provides guidance for the analysis of model behaviour and exploration of the role of key parameters. Troitzsch (2017) describes a way to reconstruct simulation models along the line of the ‘non-statement view of models’ and explains how such a reformulation can increase the transparency of the simulations, and the functioning of the models. For more complex models, particularly those geared towards policy evaluation, Scherer et al. (2015) outline a framework focusing on the implementation of traces, which are designed in a way such that the output of the model can be linked to the initial input of stakeholders, the background knowledge and specific model design decisions. This framework is more complex and currently implemented for one particular class of models, yet it has the potential to help not only modellers, but all stakeholders of a model to better understand what the model does, why it does it, and how this can be justified given the background information available. For similar expositions that seek to make verification more open and inclusive, see also Wimmer et al. (2012) or Lotzmann & Wimmer (2013).
Of course, several of the frameworks surveyed in the introduction can also help to make models more transparent. In all, the more transparent the model, the easier verification: a model that is written in simplified equations, well-documented computer code or a clear language is - ceteris paribus - easier to be verified than other models.
We now move to model validation. There are several forms of validation and they partly echo the different perceptions researchers have in mind when they talk about ‘understanding reality’ (see above). At least the following four forms of model validation can be distinguished (Tesfatsion 2017):
- Input validation
- Process validation
- Descriptive output validation
- Predictive output validation
In contrast to verification, these four activities assess the relation of the model to reality[13]. I will discuss the four forms one by one and relate them to each other in the next sub-section. In the appendix I relate this terminology to that of Augusiak et al. (2014).
Input validation - as illustrated in Figure 4b - assesses the ability of the model at \(t = 0\) to represent certain aspects of the system under investigation, i.e., to impute many properties correctly on the target. In an ABM of a financial market, for example, input validation concerns the question of whether the number of traders is similar in the real market and the ABM, whether their initial wealth distribution is the same, or whether their decision-making procedures match. Some inputs to a model are easier to validate than others: while the initial wealth distribution of the trader just mentioned might be inferred from empirical data, their decision making algorithms might never been identified precisely, yet there are without doubt more and less accurate descriptions of their decision making.
Generally, it is always easier to validate aspects of a model that are a direct representation of real-world objects (Schulze et al. 2017). For example, human beings are boundedly rational, use heuristics and do not directly maximize something such as utility (Gigerenzer 2015). So, representing human beings not as locally constructive and boundedly rational agents, but as utility-maximizers might be a valid and useful modelling approach, but it makes it much more difficult to validate the model in terms of input-validation (Schlüter et al. 2017). Furthermore, input validation is facilitated if aspects of reality are represented explicitly: If in our model of the financial market, traders explicitly trade directly with each other, the interaction network specifying their inter-action structure can be validated against real-world data. This requires the model to be sufficiently complex. If we use indirect representations to keep the model simple, e.g. an Walrasian auctioneer[14], input validation becomes more difficult (Balbi & Giupponi 2009).
In all, input validation is facilitated by sufficiently complex models, which avoid as-if representations and good data.
Process validation assesses the credibility of the mechanisms in the model, i.e., the mechanistic adequacy of a model (see Figure 4c). Process validation is exacerbated by the fact that in reality, “most mechanisms are concealed, so that they have got to be conjectured” (Bunge 2004, p. 186). Because mechanisms are not directly observable, no model will ever be fully process-validated. But there are many reasonable ways to assess the question of whether the implemented mechanism A is more or less likely to operate in the real world than mechanism B. These ways include expert and stakeholder validation (also known as ‘participatory validation’ Voinov & Bousquet 2010; Smajgl & Bohensky 2013), process tracing (Steel 2008, ch. 9), face validation (Klügl 2008) and a clever use of experiments (e.g. Bravo et al. 2015)[15].
It is indeed one of the main epistemological merits of ABM that they are generative, i.e., necessarily suggest mechanisms that can - in principle - be tested concerning their plausibility with regard to the target system (Epstein 2007). This is facilitated by the rise of object-oriented programming, since the distinction between instances and methods in the model facilitates the interpretative relation to real world objects and mechanisms.
What kind of models are easier accessible for process validation? First, the more direct the representation of the real objects and the mechanisms, the easier the assessment of the mechanism (Macal 2016). Object-oriented models tend to be easier to process-validate because instances in the model often correspond to objects in reality, and methods correspond (at least partly) to mechanisms. Second, a modular design also makes it – ceteris paribus – easier to process-validate a model.
Next, we turn our attention to descriptive output validation. Here one asks to what extent the output of the model can replicate existing data, i.e., to understand the dynamic sufficiency of the model (see Figure 4d). Or, referring to Figure 3a, we test whether the imputed states in \(t_1\) are correct. For example, if we have built a model for the UK economy, we may compare the time series for GDP from the model with real-world data on the GDP of the UK.
Although descriptive output validation is maybe the most commonly used form of validation (at least in economics), there are some problems with this kind of validation that one has to keep in mind:
- Empirical risk minimization: in most cases, one is interested in minimizing the prediction risk of models. Because the prediction risk of a model is unobservable, one often uses the empirical risk as an approximation or estimator for prediction risk. This is a mistake because the empirical risk is minimized by choosing a model with many free parameters, while prediction risk increases with too many free parameters.
- Overfitting: this is a direct corollary from the first point. If a model has so many free parameters that it can be calibrated to existing data very well, it is likely to perform poorly for new data.
- Equifinality: usually, we can think of many mechanisms that can bring about the same result. The mechanism-to-function mapping is many-to-one (Gräbner & Kapeller 2015, p. 435). Therefore, if we are interested in mechanism-based explanation, the calibration of a model to existing time series alone is insufficient because it tells us relatively little about what mechanisms were actually at work.
A good illustration of the limits of descriptive output validation is given by Janssen (2009) who discusses the famous Anasazi model (Axtell et al. 2002) and shows how many important questions still remain open, despite the model having a very nice fit with historical data (see also Grüne-Yanoff 2013). Without additional validation forms being applied (in this case particularly further process validation), the model can ‘explain’ the dynamics of the Anasazi only in a limited way.
What makes a model easy to validate in terms of descriptive output validation? Ceteris paribus, the more complex the model and the more free parameter it has, the more successful it will be in terms of descriptive output validation. Grimm (2005) describes the practice of ‘pattern oriented modelling’ as a less naive form of descriptive output validation. Here, one tests how several model specifications can replicate an observed pattern, eliminates the unsuccessful one and proceeds with more detailed patterns until all but a very few candidate models remain.
Finally, predictive output validation basically asks how well the model can be trained to predict future states of the system. Its idea is also illustrated in Figure 4d, but in contrast to descriptive output validation, the real world data is separated into a training set and a test set. This way, one avoids the problem of over-fitting and empirical risk minimization. This form of model validation is extremely illuminating, but not always applicable because of data requirements.
Furthermore, any form of output validation should be complemented with process validation since being able predict without knowing why one is able to predict is often problematic. To see this, consider the following example[16]: Babylonian astronomers were able to predict solar eclipses and planetary movements with astonishing accuracy more than three thousand years ago. They based these predictions on extensive and careful observations and the application of geometry, without having any deeper understanding of the causes for these movements and the physical relationships between planets, moons, and the sun. Their way of predicting solar eclipses is nevertheless successful since the periodicity of the movement of celestial bodies does not change. The periods between two solar eclipses are the same today, as they have been 3000 years ago.
The preceding example shows that making statements about the ‘validity’ of a model requires meticulous formulation. Fortunately, the kind of validation techniques just reviewed correspond closely to the different types of model validity as discussed in the philosophical literature (e.g. Grüne-Yanoff & Weirich 2010, pp. 37-41). Structural validity demands that a model both predicts the behaviour of its target and adequately represents its mechanistic structure, i.e., not only are future states predicted correctly, it is also explained how and why these states come about. To show that a model is structurally valid one has to employ all four validation techniques presented. Predictive validity requires a model to predict future behaviour of its target. This requires predictive output validation. And replicative validity requires a model to replicate the observed behaviour of the target. Consequently, it requires us to employ descriptive output validation.
Stating that a model has been validated successfully must also take into account the fidelity criteria as discussed in the previous section (see also Table 1). If a model is intended only as a very rough illustration of some isolated mechanisms, stating that it is not output validated is not a sensible statement. Yet if the same model is claimed to have predictive power, output validation becomes essential. For model developers and users, this means that they should be very explicit with regard to the fidelity criteria they employed.
Trade offs in practical modelling design
What is the relation between verification and the various types of validation? Is there a model design that scores optimal in all four activities? Unfortunately, for the single model this is usually not the case. There are trade-offs in terms of modelling design that make it practically impossible to design the ‘perfect model’.
Before turning to practical issues, we will have a short view on the philosophical literature on trade-offs in modelling. This literature dates back to Levins (1966) who discusses several modelling desiderata in the context of population modelling. He argued that there are trade-offs with regard to generality, realism, and precision of a model. More recently, Matthewson & Weisberg (2008) reconsidered Levin’s arguments and provide a clearer taxonomy of trade-offs in the context of model design.
First, they distinguish between ‘simple’ and ‘complex’ trade-offs[17]. The first correspond to pragmatic constraints: increasing the quality of the model with respect to one desideratum makes it more difficult to realize another desideratum. We will be concerned with the simple trade-offs below when we discuss whether increasing the validity of a model in one dimension makes it more difficult to keep or increase the validity in another dimension.
‘Complex trade-offs’ relate to more fundamental relationships between model desiderata that cannot be overcome by the investment of more time, thought or computational power. In the more formal part of the paper Matthewson & Weisberg (2008) prove the existence of fundamental trade-offs between the precision of a model description and the generality of the models picked up by the description. They also argue that the less homogeneous and more complex the target, the more profound the trade-offs, and the smaller the intended scope of a model, the less severe the trade-offs.
The scope and relevance of these results are still debated in philosophical literature, as are their practical implications. The interested reader might refer to the more in-depth contributions of, for example, Odenbaugh (2003), Matthewson & Weisberg (2008) or Goldsby (2013). In the following we will treat a successful model validation and verification as model desiderata and ask whether there are (simple or complex) trade-offs among them. Thus, we will ask for example, whether models that tend to be easier to verify tend to be more difficult to process validate, and so on.
As illustrated in Figure 5, I believe there are a number of such trade-offs in terms of model design. Making a model easily amendable to one kind of verification/validation makes it more cumbersome to validate/verify with another kind.
We first consider the relationship between input validation and verification. Here, researchers often face a practical trade-off because a successful input validation is facilitated by a direct and detailed representation of the system under investigation, but verification is easier if the model is more parsimonious. Also, the ease of verification due to model simplicity often comes at the expense of generality, since it is not clear to what extent the model applies to situations for which the (strict) assumptions are not applicable (Cartwright 2007).
When turning to the relationship between verification and descriptive output validation, we again observe tension in terms of model design. Descriptive output validation produces the best results for models with many degrees of freedom, while verification is easiest for simple and parsimonious models. As in the case of verification and input validation, there is a trade-off between a more complex and better validated and a simpler, better verified model.
The next relationship to be considered is that between descriptive and predictive output validation. It is very clear that there is a trade-off involved because the relationship between the two kinds of validation mimics the well-known trade-off between risk-minimization and empirical risk-minimization in inferential statistics. The more degrees of freedom we give to our model, the easier it is to calibrate it to the data we have, but the greater the risk for over-fitting.
Finally, we turn to the relationship between predictive output validation and process validation, which I believe to be complementary. There are a couple of reasons for this: Firstly, one argument in favour of representing real-world mechanisms explicitly in formal models is that such models are easier to generalize than models that do not do so, both in terms of time and space. Since training a model could be considered a generalization from small data sets, models that explain in terms of mechanism should at least not perform worse when it comes to prediction. Secondly, training a model works through letting the algorithms explore patterns in the data, and these patterns are likely to be caused by real-world mechanisms. Therefore, a model that performs well in resembling mechanisms of the target should at least not perform worse in predicting the system’s future behaviour as a model that does not capture these mechanism well. Finally, real-world mechanisms are usually unobservable. And while the techniques of process validation mentioned above are certainly effective, pro-cess validation should always be complemented by other validation techniques. Predictive output validation, if feasible, certainly seems to be an excellent choice from a practical perspective.
It is important to note that the trade-offs presented here are – except the trade-off between descriptive and predictive output validation – not formally proven. They are based on personal experience and logical consideration. Studying these trade-offs more formally and to clarify whether they count as simple of complex trade-offs in the sense of Matthewson & Weisberg (2008) is a fruitful area for future research to which both practising modellers and philosophers have something to contribute.
Validation and the purpose of a model
Considering these intricate relationships and trade-offs between various forms of verification and validation, we must ask whether there can be a reasonable prioritization among them. If this were true, one should design a model such that it maximizes its performance in terms of this form of verification and validation and then turn to the other forms one by one, depending on their respective importance. Unfortunately, such a general ranking is not feasible. Rather, what kind of verification and validation is needed depends on the purpose of a model (Mäki 2010), and the degree of validation required depends on the fidelity criteria as introduced in Section 2.
There are many purposes for modelling one could think of (see e.g. Epstein 2008). For models that are primarily geared towards the provision of adequate predictions, predictive output validation is obviously very important, yet process and input validation is only indirectly a concern. On the other hand, if a model should explain why a certain phenomenon in the past has occurred, descriptive output validation and process validation are of particular importance. In both cases, the adequate validation techniques as well as the practical design of the models differ[18].
The key message here is that depending on the purpose of the model, decisions between competing designs must be made and the decision in favour of one design might entail better performance in one kind of verification/validation at the cost of a comparatively worse performance in another kind of verification/validation.
There is no general rule for a concrete prioritization of the respective kinds of verification and/or validation. The intensity and kind of validation depends on the fidelity criteria and the purpose of the modellers. Yet the comparison among different models and their interpretation can nevertheless be facilitated if the design choices are made as transparent as possible and are explicitly justified and related to the purpose and the construal of the model. Here, my proposal aligns with existing frameworks for model presentation according to which the model purpose should be made explicit (e.g., Grimm et al. 2014). If researchers were very specific with regard to the fidelity criteria they had in mind when building a model, much mis- and abuse of models could be prevented.
While the claim that validation should follow the purpose of the model is widely accepted, there are important exceptions. As argued by Lehtinen & Kuorikoski (2007), different disciplines have different conceptions of what counts as ‘understanding’. Based on these conceptions, they may not fully subscribe to the claim that ‘validation should follow the purpose of the model’. Economists, for example, prefer parsimonious models that can be solved analytically within the maximization-cum-equilibrium approach. This constrains the set of admissible methods and validation techniques, and results in a bias towards particular forms of verification and validation in economics (in particular towards descriptive output validation)[19]. Using explicit epistemological frameworks such as the one suggested here, may facilitate identification and overcome such biases via interdisciplinary discussion and reflection.
Some Immediate Practical Implications
Two immediate practical implications for applied modelling design follow from what has been claimed in the previous sections. Firstly, there are some design principles that are at least never harmful, but frequently useful when assessing the relation between a model and reality. These are principles such as a modular modelling design and the strive for transparency and clarity in the exposition of the model. Here, the existing frameworks with regard to the functioning of models, and the epistemological framework as introduced above could be helpful. Secondly, while it may not be possible to design a model that performs very well in terms of all kinds of verification and validation, one can sometimes combine the respective strengths and weaknesses of several models via the practice of sequential modelling.
Sequential modelling refers to the practice of starting with a very simple and stylized model and then building more and more complex models that are all verified by aligning them (in the sense of Axtell et al. 1996) with the previous, simpler model. In the best case, the first and thus simplest, model is amendable to analytical proofs. Usually, such simple models are purely equation-based. One can then proceed by building an agent-based model that can be aligned with this simplest model. This way, one can “transfer” some of the rigour of the simpler model to the more complex model: by showing that the more complex model behaves –for the relevant parameterization – as a simpler and well-verified model increases our trust in the functioning of this model. On the other hand, because of its increased complexity it can be validated more rigorously (see Gräbner et al. 2017 for an example and a thorough discussion of the concept). If successful, this practice allows one to appreciate the advantages of simple models in terms of verification also for the more complex models, which have their strengths in model validation.
An example is provided by Henderson & Isaac (2017). The authors start with a general-equilibrium model of agrarian production that allows for an analytical solution. The model however, poorly represents the structure of modern agrarian production. To preserve the rigour of the original model, Henderson and Isaac develop an agent-based model that replicates the functioning of the original model. Thanks to its modular structure, the agent-based model can then be extended to include some essential features of modern agrarian production that are beyond the scope of the original model. Finally, the authors have a model that is a good representation of the reality the authors are interested in, but that is also verified because of its sequential construction.
Unfortunately, the practice of sequential modelling is not always applicable. The system under investigation must be such that a very stylized model can be at least remotely related to this system. This may not always be the case. Furthermore, when relating the increasingly complex models to each other, one faces the problem of when one model simulates another. This has been discussed more extensively in Axtell et al. (1996) under the topic of ‘Aligning Simulation Models‘ and subsequent work. Despite its potential difficulties however, there are already a couple of examples where the practice of sequential modelling has been very successful, see e.g., Axtell et al. (1996), Bednar & Page (2007), Gintis (2007), or Henderson & Isaac (2017).
Conclusion and Outlook
A number of central concepts and vocabulary from the philosophy of science have been introduced in order to equip applied modellers with the means to communicate more precisely the epistemological foundations of their models. Furthermore, the concepts and epistemological framework can be used to illustrate the various ways models can help us to understand reality. I have argued that using such frameworks is useful since they help to exemplify the different epistemological foundations of models. This way, we can more transparently justify the modelling framework we have chosen and compare the results of different models more effectively.
The resulting framework was also used to distinguish and illustrate various forms of model validation and verification. The distinction between validation and verification is meaningful since not all models are directly related to reality – yet they can nevertheless be useful in a sequential model building process and should therefore be verified. We have also seen that there are different ways to relate a model to reality (i.e., to validate it) and that there seem to be trade-offs with respect to model design: some designs facilitate verification/validation in one sense, but make it more difficult in another. Which kind of verification and validation should receive priority depends on the model purpose and its construal, yet there are some design principles that are always useful and never harmful (e.g., a modular design).
Based on these considerations it follows that different modelling approaches have different comparative advantages and disadvantages with respect to verification and validation. Agent-based models, for example, seem to have a comparative advantage in terms of input validation and process validation. A comparative disadvantage of agent-based models is model verification: while a great number of excellent verification methods exist, ABMs usually do not allow for the most successful verification technique: a mathematical proof, which is why they are characterized by a certain “epistemic opaqueness” (Humphreys 2009). Based on this observation, the practice of sequential modelling has been suggested. Similar to the idea of sequential modelling is that of using a plurality of models (e.g., Aydinonat 2017).
Finally, I want to build on our epistemological elaborations to answer two questions mentioned in the beginning: (1) “Is verification and validation necessary?” and (2) “Is verification and validation possible?”. With regard to the first question, I cannot think of any cases where model verification should not be given high priority. There are many reasons for why we should know how our models work, which is why every model in this world should be properly verified.
Validation becomes necessary as soon as we want to use a model to make informed statements about the real world (e.g., Schulze et al. 2017). This is not always the case: there are models that are not meant to be representations, or to be used for statements about real or artificial systems. For such models, validation makes no sense.
Other models are hard to validated because they do not make direct statements on reality (Ylikoski & Aydinonat 2014). This is the case for ’proof-of-concept‘ models that illustrate an idea, or a causal mechanism scheme that may later serve as a building block for more complex models (see e.g., Squazzoni & Gandelli 2013; Ylikoski & Aydinonat 2014). This however, should be clarified by the modellers in specifying carefully the scope and assignment of the model, as well as its fidelity criteria. Then, validation should take place in accordance with these specifications: the kind of validation we should seek depends on the particular kind of statement about the world we want to make. So while validation might then be a rough activity (if no precise statements about the target are attempted), but is remains necessary as soon as one uses a model to make any statements about the real world.
In effect, verification is always and validation often important. What about the feasibility of verification and validation? If we consider our framework as illustrated in Figure 4, verification is only concerned with the internal structure of a model. At least for simple mathematical models a nearly complete verification is often feasible. Verbal models can never be verified with certainty, and computational models reside somehow in the middle. So, while complete verification is possible only for a small subset of models, sufficient verification is a feasible and attractive desideratum.
Considering validation, the situation becomes more complex. Firstly, some forms of validation are easier (e.g. descriptive output validation) while others (e.g., process validation) are more difficult. Secondly, a complete validation will always remain impossible, even if one focuses on one particular form of validation (e.g. input validation). We simply cannot perceive reality in its entirety such that we could compare the model to this complete description of the real world. Even in the century of big data (in which still many data problems prevail, see Schulze et al. 2017), there will never be the perfectly validated model, also because of the trade-offs between different validation types.
Yet, the fact that complete verification and validation is impossible does not release us from the duty to strive for the best verification and validation that is appropriate for our modelling purpose, and to be transparent with regard to how we want our models to relate to reality and on how we have assessed this. Frameworks such as the one presented here hopefully facilitate this task.
Acknowledgements
An earlier version of this article has been presented as a keynote speech at the “Agent-based modelling in economics – from toy model to verified tool of analysis“ held between May 19th-20th 2017 at the ESCP Europe Business School in Berlin. I grateful to all participants for the lively discussion and the most helpful comments. I am particularly grateful to the constructive comments by Wolfram Elsner, Sylvie Geisendorf, Torsten Heinrich and Iris Lorscheid. I also benefited tremendously from the discussions at the TINT workshop “What to make of highly unrealistic models?” held between 12-13 October 2017 at the University of Helsinki and organized by Emrah Aydinonat, Till Grüne-Yanoff and Uskali Mäki. Finally, I want to acknowledge two most helpful referee reports and the useful comments by the editor of JASSS. All remaining errors are my own. This research has benefited from funds provided by the Oesterreichische Nationalbank (OeNB) under the Anniversary Fund, project number: 17383.Notes
- Its use has been encouraged by prominent outlays, including JASSS. However, it is more prominent in some disciplines (e.g. ecology), and less frequently used in others (e.g. economics). This illustrates the difficulty of introducing commonly accepted standards into a lively research community.
- Some models are not meant to represent anything, and models are not the only way to represent objects (e.g. Frigg & Nguyen 2017). But as I will justify in more detail below, this paper focuses on models as means to represent a system under investigation.
- For an excellent illustration of the consequences of different conceptions of ‘understanding’ see Lehtinen & Kuorikoski (2007) who study the reluctance of economists to use agent-based simulation models.
- Lehtinen & Kuorikoski (2007) argue that these particular epistemological preferences of economists explain why ABMs are less accepted in the economics community: economists (to a large extent) still adhere to the idea that scientific understanding “consists of the ability to logically derive conclusions with a small set of common argumentation patterns” (Lehtinen & Kuorikoski 2007, p. 324), and these “common argumentation patterns” in economics are individual rationality and optimization, as well as systemic equilibrium. Simulation models do not have their comparative advantage in this kind of explanation (see below), which is why most economists – in contrast to many other social and natural scientists – are reluctant to use them. This account of the economic way of theorizing is descriptive, and not an endorsement of this kind of theorizing. Taking such approach to theorizing seriously reminds us to value rigour and parsimony and to question whether the complexity of a model is adequate, yet in general this kind of epistemology, which is most precisely formulated by Kitcher (1989), is not desirable in a normative sense (see also Squazzoni 2017 for a critical discussion of the policy implications of the modelling style advocated in economics).
- General equilibrium models are a standard modelling approach in economics. One specifies few representative agents that maximize their utility and imposes an equilibrium restriction on the system as a whole. The classical introduction is given in Mas-Colell et al. (1995).
- For criticism see e.g., Odenbaugh (2018).
Appendix: Relating the Framework with the ‘Evaludation’ Framework of Augusiak et al. (2014)
Augusiak et al. (2014) argue that the terms ‘validation’ and ‘verification’ should be eradicated because of their ambiguity. Instead, they propose the general term ‘evaludation’. I believe that – properly defined – the terms ‘verification’ and ‘validation’ are useful and highlight the difference of studying a model itself and the relation between a model and reality. The term ‘evaludation’ blurs this distinction for the sake of generality. Nevertheless, I believe the framework and the terminology of Augusiak et al. (2014) to be extremely useful for model analysis, particularly because it is well adjusted to the natural modelling cycle. However, I think it would be useful to complement it by an explicit, epistemological framework as presented in this paper.
To facilitate this task, Table 2 relates our framework terminologies to Augusiak et al. (2014).
| Term from Augusiak et al. | Relation to verif/valid terms | Comment on the relationship |
| Data evaluation | NA | Augusiak et al. (2014) rightfully highlight this step an essential part of the modelling cycle, but it does not need to be part of an epistemological framework. |
| Conceptual model evaluation | Verification /Input validation | Augusiak et al. (2014, p. 125) consider this as the "assessment of the simplifying assumptions underlying a model’s design [...] including an assessment of whether the structure, [...] form a logically consistent model." This step has elements of model verification (e.g. the test of all assumptions are logically consistent), and validation (e.g. the assessment of the assumptions capture the essence of the real system). |
| Implementation verification | Verification | Augusiak et al. (2014, p. 125) use this step to ensure that the modelling formalism is accurate and that the computational model does what it is supposed to do. This corresponds to verification in the sense I use the term. |
| Model output verification | Input validation | Augusiak et al. (2014, p. 125) define the aim of this step as "to ensure that the individuals and populations represented in the model respond to habitat features and environmental conditions in a sufficiently similar way as their real counterparts.” This step involves some aspects of verification, but mostly corresponds to input validation. |
| Model analysis | Verification | Here, Augusiak et al. (2014) are concerned with testing the sensitivity of the model to changes in the model parameters, and the understanding of how the model results have emerged. This step is clearly about verifying the model since no link to reality is investigated. |
| Model output corroboration | Predictive output validation | In their final evaludation step, Augusiak et al. (2014, p. 125) seek to compare "model predictions with independent data and patterns that were not used, and preferably not even known, while the model was developed, parameterised, and verified." This is basically the definition of predictive output validation. |
There are two aspects regarding the relationship that are worth mentioning: Firstly, Augusiak et al. (2014) do not mention all forms of validation that are possible. I believe that what they term “Model output corroboration” might be interpreted more broadly to capture both descriptive output validation and process validations.
Secondly, the framework of Augusiak et al. (2014) is by no means incompatible with my epistemological framework. This is not surprising given the fact that both frameworks have different, yet complementary aims. From a pragmatic viewpoint, it seems to me that if both frameworks are used jointly, every step in the evaludation procedure should explicitly distinguish between activities concerned with the model, and activities assessing the link of the model with reality, and be explicit about how the latter could be established. In Figure 6, I suggest a way to accommodate explicit epistemological considerations into the evaludation framework (thereby slightly altering the terminology of Augusiak et al. 2014), but other ways to relate the framework are certainly possible.
References
ALDEN, K., Read, M., Timmis, J., Andrews, P. S., Veiga-Fernandes, H. & Coles, M. (2013). Spartan: A Comprehensive Tool for Understanding Uncertainty in Simulations of Biological Systems. PLoS Computational Biology, 9(2), e1002916. [doi:10.1371/journal.pcbi.1002916]
ARMY Corps of Engineers (1981). San Francisco Bay - Delta Tidal Hidraulic Model: User’s Manual. San Francisco: Army Corps of Engineers.
AUGUSIAK, J., Van den Brink, P. J. & Grimm, V. (2014). Merging validation and evaluation of ecological models to ‘evaludation’: A review of terminology and a practical approach. Ecological Modelling, 280, 117–128. [doi:10.1016/j.ecolmodel.2013.11.009]
AXELROD, R. (1997). Advancing the Art of Simulation in the Social Sciences. In R. Conte, R. Hegselmann & P. Terna (Eds.), Simulating Social Phenomena, (pp. 21–40). Berlin: Springer Verlag.
AXTELL, R. (2005). The Complexity of Exchange. The Economic Journal, 115(504), F193–F210. [doi:10.1111/j.1468-0297.2005.01001.x]
AXTELL, R., Axelrod, R., Epstein, J. M. & Cohen, M. D. (1996). Aligning Simulation Models: A Case Study and Results. Computational and Mathematical Organization Theory, 1(2), 123–141.
AXTELL, R. L., Epstein, J. M., Dean, J. S., Gumerman, G. J., Swedlund, A. C., Harburger, J., Chakravarty, S., Hammond, R., Parker, J. & Parker, M. (2002). Population growth and collapse in a multiagent model of the Kayenta Anasazi in Long House Valley. Proceedings of the National Academy of Sciences, 99(Supplement 3), 7275–7279. [doi:10.1073/pnas.092080799]
AYDINONAT, N. E. (2017). The Diversity of Models as a Means to Better Explanations in Economics. SSRN Electronic Journal.
BALBI, S. & Giupponi, C. (2009). Reviewing agent-based modelling of socio-ecosystems: A methodology for the analysis of climate change adaptation and sustainability. University Ca Foscari of Venice, Dept. of Economics Research Paper Series, 15(9). [doi:10.2139/ssrn.1457625]
BAUMGÄRTNER, S., Becker, C., Frank, K., Müller, B. & Quaas, M. (2008). Relating the philosophy and practice of ecological economics: The role of concepts, models, and case studies in inter- and transdisciplinary sustain-ability research. Ecological Economics, 67(3), 384–393.
BECK, K. (2002). Test Driven Development: By Example. Boston, MA: Addison-Wesley Professional.
BEDNAR, J. & Page, S. (2007). Can Game(s) Theory Explain Culture?: The Emergence of Cultural Behavior Within Multiple Games. Rationality and Society, 19(1), 65–97.
BISSELL, C. (2007). Historical perspectives - The Moniac A Hydromechanical Analog Computer of the 1950s. IEEE Control Systems, 27(1), 69–74. [doi:10.1109/MCS.2007.284511]
BOERO, R. & Squazzoni, F. (2005). Does Empirical Embeddedness Matter? Methodological Issues on Agent-Based Models for Analytical Social Science. Journal of Artificial Societies and Simulation, 8(4), 6: https://www.jasss.org/8/4/6.html.
BRAVO, G., Squazzoni, F. & Takács, K. (2015). Intermediaries in Trust: Indirect Reciprocity, Incentives, and Norms. Journal of Applied Mathematics, 2015(3), 1–12. [doi:10.1155/2015/234528]
BUNGE, M. (2004). How Does It Work? The Search for Explanatory Mechanisms. Philosophy of the Social Sciences, 34(2), 182–210.
CAPALDO, J. (2014). The Trans-Atlantic Trade and Investment Partnership: European Disintegration, Unemploy-ment and Instability. Global Development and Environment Institute Working Paper, 14-03.
CARTWRIGHT, N. (2007). Hunting Causes and Using Them. Cambridge, UK: Cambridge University Press.
CARTWRIGHT, N. (2010). Models: Parables v Fables. In R. Frigg & M. C. Hunter (Eds.), Beyond Mimesis and Convention Representation in Art and Science. John Wiley & Sons, 19–31. [doi:10.1007/978-90-481-3851-7_2]
DEATON, A. (2010). Instruments, Randomization, and Learning about Development. Journal of Economic Literature, 48(2), 424–455.
EINSTEIN, A. (1949). Remarks Concerning the Essays Brought together in this Co-operative Volume. In P. A. Schilpp (Ed.), Albert Einstein Philosopher-Scientist, (pp. 665–688). Evanston, IL.
EPSTEIN, J. M. (2006). Remarks on the Foundations of Agent-Based Generative Social Science. In L. Tesfatsion & K. L. Judd (Eds.), Handbook of Computational Economics, (pp. 1585–1604). Elsevier: Amsterdam.
EPSTEIN, J. M. (2007). Generative Social Science: Studies in Agent-Based Computational Modeling. Princeton, IL: Princeton University Press.
EPSTEIN, J. M. (2008). Why Model? Journal of Artificial Societies and Simulation, 11(4), 12: https://www.jasss.org/11/4/12.html
EUBANK, S., Guclu, H., Anil Kumar, V. S., Marathe, M. V., Srinivasan, A., Toroczkai, Z. & Wang, N. (2004). Modelling disease outbreaks in realistic urban social networks. Nature, 429(6988), 180–184. [doi:10.1038/nature02541]
EVANS, G. W. & Honkapohja, S. (2005). An Interview with Thomas J. Sargent. Macroeconomic Dynamics, 9(4), 561–583.
FAGIOLO, G., Moneta, A. & Windrum, P. (2007). A Critical Guide to Empirical Validation of Agent-Based Models in Economics: Methodologies, Procedures, and Open Problems. Computational Economics, 30(3), 195–226. [doi:10.1007/s10614-007-9104-4]
FISHER, R. (1930). The Genetical Theory of Natural Selection. Oxford: The Clarendon Press.
FORRESTER, J. W. (1971). Counterintuitive behavior of social systems. Theory and Decision, 2(2), 109–140. [doi:10.1007/BF00148991]
FRANCOIS, J., Manchin, M., Norberg, H., Pindyuk, O. & Tomberger, P. (2013). Reducing Trans-Atlantic Barriers to Trade and Investment. Final Project Report for the European Commission.
FRIGG, R. & Nguyen, J. (2016). The Fiction View of Models Reloaded. The Monist, 99(3), 225–242. [doi:10.1093/monist/onw002]
FRIGG, R. & Nguyen, J. (2017). Models and Representation. In L. Magnani & T. Bertolotti (Eds.), Springer Handbook of Model-Based Science, (pp. 49–102). Dordrecht, Heidelberg, London and New York.
FRIGG, R. & Reiss, J. (2008). The philosophy of simulation: Hot new issues or same old stew? Synthese, 169(3), 593–613. [doi:10.1007/s11229-008-9438-z]
GELFERT, A. (2016). How to Do Science with Models. Berlin Heidelberg: Springer.
GELFERT, A. (2017). The Ontology of Models. In L. Magnani & T. Bertolotti (Eds.), Springer Handbook of Model-Based Science. Dordrecht et al.: Springer, pp. 5–24. [doi:10.1007/978-3-319-30526-4_1]
GIERE, R. N. (1990). Explaining Science: A Cognitive Approach. Chicago and London: University of Chicago Press.
GIGERENZER, G. (2015). Simply Rational. Decision Making in the Real World. Oxford: Oxford University Press. [doi:10.1093/acprof:oso/9780199390076.001.0001]
GINTIS, H. (2007). The Dynamics of General Equilibrium. The Economic Journal, 117, 1280–1309.
GOLDSBY, M. (2013). The “structure” of the “strategy”: Looking at the Matthewson-Weisberg trade-off and its justificatory role for the multiple-models approach. Philosophy of Science, 80(5), 862–873. [doi:10.1086/673728]
GRÄBNER, C., Bale, C. S. E., Furtado, B. A., Álvarez Pereira, B., Gentile, J. E., Henderson, H. & Lipari, F. (2017). Getting the Best of Both Worlds? Developing Complementary Equation-Based and Agent-Based Models. Computational Economics, In Press. [doi:10.1016/10.1007/s10614-017-9763-8]
GRÄBNER, C. & Kapeller, J. (2015). New Perspectives on Institutionalist Pattern Modeling: Systemism, Complexity, and Agent-Based Modeling. Journal of Economic Issues, 49(2), 433–440. [doi:10.1080/00213624.2015.1042765]
GRIMM, V. (2005). Pattern-Oriented Modeling of Agent-Based Complex Systems: Lessons from Ecology. Science, 310(5750), 987–991.
GRIMM, V., Augusiak, J., Focks, A., Frank, B. M., Gabsi, F., Johnston, A. S. A., Liu, C., Martin, B. T., Meli, M., Radchuk, V., Thorbek, P. & Railsback, S. F. (2014). Towards better modelling and decision support: Documenting model development, testing, and analysis using TRACE. Ecological Modelling, 280, 129–139. [doi:10.1016/j.ecolmodel.2014.01.018]
GRIMM, V., Berger, U., Bastiansen, F., Eliassen, S., Ginot, V., Giske, J., Goss-Custard, J., Grand, T., Heinz, S. K., Huse, G., Huth, A., Jepsen, J. U., Jørgensen, C., Mooij, W. M., Müller, B., Pe’er, G., Piou, C., Railsback, S. F., Robbins, A. M., Robbins, M. M., Rossmanith, E., Rüger, N., Strand, E., Souissi, S., Stillman, R. A., Vabø, R., Visser, U. & DeAngelis, D. L. (2006). A standard protocol for describing individual-based and agent-based models. Ecological Modelling, 198(1-2), 115–126.
GRIMM, V., Berger, U., DeAngelis, D. L., Polhill, J. G., Giske, J. & Railsback, S. F. (2010). The ODD protocol: A review and first update. Ecological Modelling, 221(23), 2760–2768. [doi:10.1016/j.ecolmodel.2010.08.019]
GRÜNE-YANOFF, T. (2008). Learning from Minimal Economic Models. Erkenntnis, 70(1), 81–99.
GRÜNE-YANOFF, T. (2013). Teaching philosophy of science to scientists: Why, what and how. European Journal for Philosophy of Science, 4(1), 115–134. [doi:10.1007/s13194-013-0078-x]
GRÜNE-YANOFF, T. (2015). Why behavioural policy needs mechanistic evidence. Economics and Philosophy, 32(3), 463–483.
GRÜNE-YANOFF, T. & Weirich, P. (2010). The Philosophy and Epistemology of Simulation: A Review. Simulation & Gaming, 41(1), 20–50. [doi:10.1177/1046878109353470]
HENDERSON, H. & Isaac, A. G. (2017). Modern value chains and the organization of agrarian production. American Journal of Agricultural Economics, 99(2), 379-400. [doi:10.1093/ajae/aaw092]
HUMPHREYS, P. (2009). The philosophical novelty of computer simulation methods. Synthese, 169(3), 615–626. [doi:10.1007/s11229-008-9435-2]
JANSSEN, M. A. (2009). Understanding artificial Anasazi. Journal of Artificial Societies and Simulation, 12(4), 13: https://www.jasss.org/12/4/13.html.
JOHNSON-LAIRD, P. (2005). Mental models and thought. In K. J. Holyoak & R. G. Morrison (Eds.), The Cambridge Handbook of Thinking and Reasoning. Cambridge, UK, pp. 185-208.
KITCHER, P. (1989). 'Explanatory Unification and the Causal Structure of the World.' In P. Kitcher & W. C. Salmon (Eds.), Scientific Explanation. Minneapolis, MN, pp. 410-505.
KLÜGL, F. (2008). A validation methodology for agent-based simulations. In The 2008 ACM symposium, (p. 39). New York, New York, USA: ACM Press. [doi:10.1145/1363686.1363696]
KUORIKOSKI, J., Lehtinen, A. & Marchionni, C. (2010). Economic modelling as robustness analysis. The British Journal for the Philosophy of Science, 61(3), 541–567.
LEE, J.-S., Filatova, T., Ligmann-Zielinska, A., Hassani-Mahmooei, B., Stonedahl, F., Lorscheid, I., Voinov, A., Pol-hill, G., Sun, Z. & Parker, D. C. (2015). The complexities of agent-based modeling output analysis. Journal of Artificial Societies and Simulation, 18(4), 4: https://www.jasss.org/18/4/4.html. [doi:10.18564/jasss.2897]
LEHTINEN, A. & Kuorikoski, J. (2007). Computing the perfect model: Why do economists shun simulation? Philosophy of Science, 74(3), 304–329.
LEVINS, R. (1966). The strategy of model Building in population biology. American Scientist, 54(4), 421–431.
LISCIANDRA, C. (2016). Robustness analysis and tractability in modeling. European Journal for Philosophy of Science, 7(1), 79–95.
LORSCHEID, I., Heine, B.-O. & Meyer, M. (2011). Opening the ‘black box’ of simulations: Increased transparency and effective communication through the systematic design of experiments. Computational and Mathematical Organization Theory, 18(1), 22–62. [doi:10.1007/s10588-011-9097-3]
LOTZMANN, U. & Wimmer, M. A. (2013). Traceability In Evidence-Based Policy Simulation. In 27th Conference on Modelling and Simulation, (pp. 696–702). ECMS.
MACAL, C. M. (2016). Everything you need to know about agent-based modelling and simulation. Journal of Simulation, 10(2), 144–156. [doi:10.1057/jos.2016.7]
MÄKI, U. (2010). Models and Truth: The Functional Decomposition Approach. In M. Suárez, M. Dorato & M. Redei (Eds.), EPSA Epistemology and Methodology of Science, (pp. 177–188). Heidelberg, London, New York.
MAS-COLELL, A., Whinston, M. D. & Green, J. R. (1995). Microeconomic Theory. New York, NY, Oxford, UK: Oxford University Press.
MATTHEWSON, J. & Weisberg, M. (2008). The structure of tradeoffs in model building. Synthese, 170(1), 169–190.
MORGAN, M. S. & Morrison, M. (Eds.) (1999). Models as Mediators. New York, NY: Cambridge University Press. [doi:10.1017/CBO9780511660108]
MÜLLER, B., Balbi, S., Buchmann, C. M., de Sousa, L., Dressler, G., Groeneveld, J., Klassert, C. J., Le, Q. B., Millington, J. D. A., Nolzen, H., Parker, D. C., Polhill, J. G., Schlüter, M., Schulze, J., Schwarz, N., Sun, Z., Taillandier, P., Weise, H. (2014). Standardised and transparent model descriptions for agent-based models: Current status and prospects. Environmental Modelling & Software, 55, 156–163.
MÜLLER, B., Bohn, F., Dressler, G., Groeneveld, J., Klassert, C., Martin, R., Schlüter, M., Schulze, J., Weise, H. & Schwarz, N. (2013). Describing human decisions in agent-based models – ODD + D, an extension of the ODD protocol. Environmental Modelling & Software, 48, 37–48. [doi:10.1016/j.envsoft.2013.06.003]
NGUYEN, J. (2016). How Models Represent. Ph.D. thesis, London School of Economics and Political Science, London.
ODENBAUGH, J. (2003). Complex systems, trade-offs, and theoretical population biology: Richard Levin’s "Strategy of Model Building in Population Biology" revisited. Philosophy of Science, 70(5), 1496–1507. [doi:10.1086/377425]
ODENBAUGH, J. (2018). Models, models, models: A deflationary view. Synthese, 47(4), 1–16.
PESCHARD, I. (2011). Making sense of modeling: Beyond representation. European Journal for Philosophy of Science, 1(3), 335–352. [doi:10.1007/s13194-011-0032-8]
RAND, W. & Rust, R. T. (2011). Agent-based modeling in marketing: Guidelines for rigor. International Journal of Research in Marketing, 28(3), 181–193.
REISS, J. (2011). A Plea for (Good) Simulations: Nudging Economics Toward an Experimental Science. Simulation Gaming, 42(2), 243–264. [doi:10.1177/1046878110393941]
RODRIK, D., Subramanian, A. & Trebbi, F. (2004). Institutions rule: The primacy of institutions over geography and integration in economic development. Journal of Economic Growth, 9, 131–165.
SCHERER, S., Wimmer, M., Lotzmann, U., Moss, S. & Pinotti, D. (2015). Evidence Based and Conceptual Model Driven Approach for Agent-Based Policy Modelling. Journal of Artificial Societies and Simulation, 18(3), 14: https://www.jasss.org/18/3/14.html. [doi:10.18564/jasss.2834]
SCHLÜTER, M., Baeza, A., Dressler, G., Frank, K., Groeneveld, J., Jager, W., Janssen, M. A., McAllister, R. R. J., Müller, B., Orach, K., Schwarz, N. & Wijermans, N. (2017). A framework for mapping and comparing behavioural theories in models of social-ecological systems. Ecological Economics, 131, 21–35.
SCHMOLKE, A., Thorbek, P., Chapman, P. & Grimm, V. (2010). Ecological models and pesticide risk assessment: Current modeling practice. Environmental Toxicology and Chemistry, 29(4), 1006–1012. [doi:10.1002/etc.120]
SCHULZE, J., Müller, B., Groeneveld, J. & Grimm, V. (2017). Agent-Based Modelling of Social-Ecological Systems: Achievements, Challenges, and a Way Forward. Journal of Artificial Societies and Simulation, 20(2), 8: https://www.jasss.org/20/2/8.html.
SMAJGL, A. & Bohensky, E. (2013). Behaviour and space in agent-based modelling: Poverty patterns in East Kalimantan, Indonesia. Environmental Modelling & Software, 45, 8–14. [doi:10.1016/j.envsoft.2011.10.014]
SQUAZZONI, F. (2017). 'Towards a Complexity-Friendly Policy: Breaking the Vicious Circle of Equilibrium Thinking in Economics and Public Policy.' In J. Johnson, A. Nowak, P. Ormerod, B. Rosewell & Y.-C. Zhang (Eds.), Non-Equilibrium Social Science and Policy. Berling Heidelberg, Springer Verlag, pp. 135–148.
SQUAZZONI, F. & Gandelli, C. (2013). Opening the black-box of peer review: An agent-based model of scientist behaviour. Journal of Artificial Societies and Simulation, 16(2), 3: https://www.jasss.org/16/2/3.html. [doi:10.18564/jasss.2128]
STACHOWIAK, H. (1973). Allgemeine Modelltheorie. Vienna and New York: Springer.
STEEL, D. (2004). Social mechanisms and causal inference. Philosophy of the Social Sciences, 34(1), 55–78. [doi:10.1177/0048393103260775]
STEEL, D. P. (2008). Across the Boundaries. Extrapolation in Biology and Social Science. Oxford, UK, New York, NY: Oxford University Press.
STEUP, M. (2016). 'Epistemology.' In E. N. Zalta (Ed.), The Stanford Encyclopedia of Philosophy, Stanford.
SUN, Z. & Müller, D. (2013). A framework for modeling payments for ecosystem services with agent-based models, Bayesian belief networks and opinion dynamics models. Environmental Modelling & Software, 45, 15–28.
TEN BROEKE, G., van Voorn, G. & Ligtenberg, A. (2016). Which Sensitivity Analysis Method Should I Use for My Agent-Based Model? Journal of Artificial Societies and Simulation, 19(1)?: www.jasss.
TESFATSION, L. (2017). Modeling economic systems as locally-constructive sequential games. Journal of Economic Methodology, 24(4), 384–409.
TROITZSCH, K. G. (2017). Axiomatic theory and simulation: A philosophy of science perspective on Schelling’s segregation model. Journal of Artificial Societies and Simulation, 20(1), 10: https://www.jasss.org/20/1/10.html. [doi:10.18564/jasss.3372]
VOINOV, A. & Bousquet, F. (2010). Modelling with stakeholders? Environmental Modelling & Software, 25(11), 1268–1281.
WEBER, M. (1922). Die Objektivität sozialwissenscha licher und sozialpolitischer Erkenntnis. In Gesammelte Aufsätze zur Wissenscha slehre, (pp. 146–214). Tübingen, DE.
WEISBERG, M. (2006). Robustness analysis. Philosophy of Science, 73(5), 730–742.
WEISBERG, M. (2007). Who is a modeler? The British Journal for the Philosophy of Science, 58(2), 207–233. [doi:10.1093/bjps/axm011]
WEISBERG, M. (2013). Simulation and Similarity. New York, NY: Oxford University Press.
WIMMER, M. A., Furdik, K., Bicking, M., Mach, M., Sabol, T. & Butka, P. (2012). 'Open Collaboration in Policy Development: Concept and Architecture to Integrate Scenario Development and Formal Policy Modelling.' In Empowering Open and Collaborative Governance, (pp. 199–219). Berlin, Heidelberg: Springer. [doi:10.1007/978-3-642-27219-6_11]
WOODWARD, J. (2006). Some varieties of robustness. Journal of Economic Methodology, 13(2), 219–240.
YLIKOSKI, P. & Aydinonat, N. E. (2014). Understanding with theoretical models. Journal of Economic Methodology, 21(1), 19–36. [doi:10.1080/1350178X.2014.886470]
