Introduction
To cope with rapid changes in the business environment, enterprises that traditionally rely exclusively on internal resources to compete in the market are gradually becoming unable to keep up with commercial developments and are thus beginning to employ new models and tools to speed up their decision-making and improve performance. Crowdsourcing is one way that has aroused considerable attention recently (Chiu et al. 2014).
Crowdsourcing is an act of outsourcing a task once performed by internal employees rather than a designated contractor in the form of an open call (Howe 2006) to the ‘crowd’. This call can provide more alternatives for an enterprise’s strategy and also reduces operational costs. The advantages of crowdsourcing have been proven in many business practices. For example, 60% of Procter & Gamble’s new product development tasks were accomplished by external crowds. In another example, the rapid iterative updating of the millet company MIUI system also benefitted from feedback from its online community users.
However, due to the unknown identity and uncontrollable behaviour of these solvers, there is a great deal of potential risk in crowdsourcing implementation processes. One risk is the deceptive behaviour of solvers caused by asymmetric information (Kannangara & Uguccioni 2013). Specifically, in order to earn a certain reward (mostly points), certain solvers without appropriate skill may deliberately conceal their skill level and submit low quality solutions, causing difficulties for employers later on (Jian-gang 2015).
A practice survey proved that most crowdsourcing projects involve a large number of these less than honest operators (Frei 2009). This is due to the fact that almost all solver recruitment is based upon a self-selection principle. Namely, the crowd voluntarily decides whether or not to participate following the enterprises’ call for tasks. Although enabling enterprises to recruit more solvers with different backgrounds, this approach could intermingle both good solutions with not so good ones. Therefore, it is necessary to screen solvers. Eickhoff et al. (2011) confirmed that the efficacy of screening, based on task characteristics, can improve the crowdsourcing process. Schenk & Guittard (2011) also argued that different tasks, such as routine tasks, creative tasks and complex tasks, all need different types of solvers. However, these studies fail to reveal the relationship that matches each task type with the relevant solver type, creating a lack of theoretical basis for enterprises to select solvers according to task. In this study, we will try to address this problem.
Basically, crowdsourcing is an online and distributed problem-solving model (Brabham 2008), whereas the NK model is a theoretical tool effective for characterizing the complexity of problem solving (e.g., Levinthal 1997; Winter et al. 2007). The NK model was introduced into crowdsourcing research by Afuah & Tucci (2012), fundamental for the rationale of this paper. Thus, taking task structure as a characteristic to distinguish task types, and taking bounded rationality as an individual factor to distinguish solver types, an agent-based model that simulates the crowdsourcing problem-solving process was constructed in this study. This was achieved by combining NK fitness landscapes with TCPE, a framework depicting crowdsourcing process, to investigate the impact of task structure and individual bounded rationality on crowdsourcing performance. The purpose of the study is to capture the matching relationship between task types and solver types. The conclusions could provide a theoretical basis and practical guidance for enterprises when designing screening mechanism for solver recruitment.
The paper is organized as follows: In Section 2, there is a brief literature review on task structure and individual bounded rationality, introducing the focus of the article. In Section 3, we present the simulation methodology and its application to our study. In Section 4, we present the simulation results and some relevant propositions inferred from the results. In Section 5, we summarize the main conclusions and discuss the study by highlighting its theoretical contributions. The last section discusses the implications of our study to management practice and further research.
Related work
Task structure
There has been various categorization with regard to types of crowdsourcing task, depending on which characteristic is deemed vital to a crowdsourcing task. For example, Rouse (2010) put forward a simple classification based on task complexity, including simple tasks, sophisticated tasks and moderate tasks. Schenk & Guittard (2011) looked specifically at task type suitable for crowdsourcing, including simple tasks such as data collection, complex tasks with innovation projects and creative tasks in fields such as art and design. Brabham (2012) divided tasks into independent tasks and interdependent tasks, stating that the former can be solved on an individual basis, whereas the latter calls for a community of problem solvers.
In addition, there is another important dimension to task classification, i.e., task structure. A typical structure-based task classification divides them into well-structured tasks and unstructured tasks (Nakatsu 2014). Well-structured tasks are those whose solutions or crowd contributions are clearly defined. For unstructured tasks without any defined solution or approach, creativity and inventiveness are essential. However, this structure-based task classification is relatively general because it simply accounts for restricted understanding of the internal structure of tasks. Therefore, task structure describing in detail the intrinsic complicated relationships among non-independent subtasks (Dennis et al. 1999) deserves further research, as it not only directly determines the complexity of the task but also indirectly affects the problem-solving process. Indeed, decision-making researchers defined task structure as a function of the number of alternative subtasks and the number of attributes in each alternative (e.g., Simon 1973; Abdolmohammadi 1999). According to this definition, we argue that the task structure can be characterized effectively by an influence matrix, which, first introduced by Steward (1981), is mainly used to as a tool for systems design (Rivkin & Siggelkow 2007). In brief, if a system contains \(N\) elements, an \(N \times N\) influence matrix can record the relationships among non-independent elements. The (\(i\), \(j\)) th entry of the influence matrix is marked by an “\(\times\)” if column element \(j\) influences the contribution of row element \(i\), and is otherwise blank.
In this study, three influence matrices summarized by Rivkin and Siggelkow (2003) were selected, including a local matrix, small-world matrix and random matrix. This was because, although each element in each matrix is affected by the same number of other elements in the corresponding influence matrix, the number of elements affected by each element varies from one to another. In other words, the three influence matrices can characterize structural differences of various tasks under certain task complexity, which has not previous been reported. More importantly, this difference in task structure can also be found in reality. Some realistic observations have revealed that decisions vary in their influence on a crowdsourcing task. In certain crowdsourcing tasks, the influence of all decisions is almost the same, whereas other decisions have a larger influence than others. As a result, the influence of task decisions can be used to account for differences in task structure.
In summary, we divided the tasks into three types based upon the three influence matrices derived from a perspective of task structure, including local structure tasks, the small-world structure tasks and random structure tasks.
Individual bounded rationality
The rationale of focusing on the bounded rationality of solver is based on Internet users in the real world. Internet users from all walks of life are involved in crowdsourcing for different motivations such as interest, achievement, or money (Organisciak 2010). Due to differences in the social division of labour, the knowledge of these users is limited and quite diversified, which therefore seriously effects the quality of problem solutions and has become one of the major concerns of enterprises when apply crowdsourcing.
As for bounded rationality, Simon (1955) considers rationality and bounded rationality as two opposite states from a discrete perspective. There is another perspective in which complete rationality and irrationality are viewed as opposing ends of a continuum of behaviour, where bounded rationality is somewhere in between (Shafir & LeBoeuf 2002). This paper uses the second perspective as it accentuates bounded rationality to the part of rationality.
Cognitive psychology argues that unless an individual has inherently "infinite knowledge", it is not possible for him/her to envision the full dimensions of a task, nor can he/she completely specify the possible causal linkage between these dimensions (Simon 1955). Thus, an individual’s attention is often transferred to several important or easily observed dimensions. As a result, a cognitive structure smaller than the problem space of a task is temporarily constructed, accordingly called “cognitive representation”. Thus, bounded rationality is manifested primarily in the limited cognitive representations that individuals use to form mental models of their own environment (e.g., Gavetti & Levinthal 2000; Kasthurirathna et al. 2016).
Furthermore, according to differences in expertise and experience due to different developmental environments and professional backgrounds, solvers can be divided into either professional or ordinary users. However, it cannot be over-emphasized that we need to learn how to distinguish professional users from ordinary users. Some early problem perception studies found that there is a difference between professional and ordinary users in the degree of their cognitive representations, as professionals often recall more relevant information when faced with a new problem (e.g., Randel & Pugh 1996; Chi et al. 1981).
However, subsequent studies argued that this difference is manifested more in the content of the solver’s cognitive representations. Owing to their knowledge of non-mathematical semantic descriptions of problem composition and their relationships (de Kleer 1990), in addition to considering a number of task elements, professional users can also identify certain key elements and their relationships based on their expertise (e.g., Joseph & Patel 1990; Sánchez-Manzanares et al. 2008). In contrast, although ordinary users can also consider only a limited number of elements, these elements are selected randomly relying on their subjective faith in a problem (Rowe & McKenna 2001). According to recent interpretations, a concept called “bounded rationality bias” was introduced to differentiate professional from ordinary users.
Bias is defined as an erroneous response that constitutes departure from normative rules or standards (Gilovich et al. 2002). Specifically, it is described as the degree of cognition deviating from rational choice in cognitive psychology, which may in turn lead to inaccuracy and errors of individual cognition (Oreg & Bayazit 2009). Therefore, we define bounded rationality bias as the extent to which key elements are chosen for cognitive representations, which reflect the accuracy of cognitive representations. In general, as professional users can identify more key elements than ordinary ones, their bounded rationality bias is relatively low, whereas that of ordinary users is relatively high.
The Model
Overview
Crowdsourcing can be employed to solve problems such as designing a new product, helping monetize a new idea, developing an enterprise strategy and so on (Chiu et al. 2014). Indeed, a problem may have many potential solutions. Although it is difficult to predict in early stages which will produce optimum results, any potential solution has certainly more than one dimension and synergy of these dimensions can affect performance (e.g., Levinthal & March 1981; Siggelkow & Levinthal 2003). More importantly, all potential solutions can constitute a problem space and the essence of problem-solving lies in the process of searching for an optimal solution within this problem space. The NK model can generate this type of problem space well, where solvers perform their search for solutions (Levinthal 1997), and searching for a solution can be seen as a process of adaptive walking on rugged problem landscape (Rivkin & Siggelkow 2007). Adaptive walking is defined as the process from an initial entity, via fitter neighbours, to either locally or globally optimal entities that are fitter than their neighbours (Kauffman & Levin 1987).
The NK model was originally developed in evolutionary biology. Levinthal (1997) first applied this model to management literature. Since this seminal work in 1997, an increasing body of literature in management has applied the NK model (e.g., Levinthal & March 1981; Gavetti & Levinthal 2000; Rivkin & Siggelkow 2003; Siggelkow & Levinthal 2003; Xu et al. 2016) and the model has been regarded as an important theoretical tool to analyse problem solving. For instance, Lazer & Friedman (2007) applied the model to examine the impact of network structure on collective problem solving. Recently, Afuah & Tucci (2012) used the NK model to qualitatively elaborate the connotation of the crowdsourcing problem-solving process. Later, inspired by Afuah & Tucci (2012), Natalicchio et al. (2017) used the NK model to simulate the search for solutions conducted by problem solvers in several crowdsourcing scenarios. However, existing studies using the NK model to study crowdsourcing, all directly introduced NK model into their studies, but seldom combined it with the crowdsourcing process. Consequently, the simulation models by these researchers does not reflect the essential characteristics of crowdsourcing problem solving. Thus, this paper constructs an agent-based model that simulates the process of crowdsourcing problem solving by combining the NK model with crowdsourcing process to fill this theoretical gap.
Basic model
The NK model was first introduced by Kauffman based on Wright's (1931, 1932) notion of a fitness landscape (e.g., Kauffman 1993; Solow et al. 1999). Fitness landscapes were used to link \(N\) gendes (or attributes) of an organism to an overall fitness level (Wright 1931). Each gene in fitness landscapes contributes to its overall fitness. However, since there may exist some interactions among genes, the contribution of a gege to the overall fitness may depend on its allele, which is the form of a gene and those of other genes that interact with it (Wright 1931). Based on this, two parameters are identified in the NK model, including the number of attributes that determine the fitness of an organism (\(N\)) and the number of interactions of each attribute with others (\(K\)). The parameter \(K\) acts on the shape of the landscapes (Levinthal 1997). Kauffman (1993) showed that low interaction among attributes, denoted by a low value of \(K\), generates a relatively smooth landscape with few valleys and peaks. Simultaneously, as \(K\) increases, the landscape becomes increasingly rugged, with especially \(K=N-1\) describing a maximally rugged landscape. Many frameworks have been proposed to describe crowdsourcing process including frameworks such as the "Task-Crowd-Process-Evaluation" (TCPE), first proposed by Chiu et al. (2014). The TCPE framework divides key elements related to crowdsourcing into four basic components (Figure 1 illustrates TCPE framework), including the task, the crowd, the process and the evaluation. TCPE succinctly and clearly portrays the crowdsourcing process, thus is used as a theoretical basis for modelling in this study. Based on the NK model, this paper modelled the four basic components under TCPE framework as follows:

The task component
A task is usually characterized by \(N\) decisions, in which it is assumed that each decision can take on two possible values of either 0 or 1 (Gavetti & Levinthal 2000; Levinthal 1997) . Accordingly, there are \(2^N\) possible potential solutions for a task in its fitness landscape. The shape of the fitness landscape is determined by the task structure that describes the intrinsic complicated relationships among non-independent decisions. In order to characterize the task structure, a type of \(N \times N\) influence matrix, in which each decision is affected by other \(K\) decisions, was introduced here. The value of \(K\) represents the task complexity. The larger the \(K\) value, the higher the task complexity. However, the internal structure of all tasks is not the same under a certain \(K\), because each decision varies in the number of other decisions that affect it (Wall 2018). In other words, under a certain \(K\), each decision is affected by other \(K\) decisions, but each decision does not affect the same number of other decisions. Therefore, three influence matrices with a similar \(K\) but different internal structures were selected here. These are a local matrix, a small-world matrix and a random matrix, representing three types of task structure respectively (see Figure 2).
Local task In the local influence matrix, each element is assumed to be influenced by its \(K / 2\) neighbours on either side, as shown in Figure 2a. As a result, for the task of the local structure, viz. local task, each decision is affected by other \(K\) decisions and each decision affects the same number of other decisions. In other words, each decision has an influence similar to the influence that others have under certain task complexity.
Small-world task In the small-world influence matrix, most elements are affected by its \(K / 2\) neighbours on either side, as shown in Figure 2b. According to the algorithm proposed by Watts & Strogatz (1998), the small-world influence matrix is established by exchanging every non-diagonal element in the local matrix with the probability \(\rho = 0.33\) to other random positions in this row. Therefore, for the task of small-world structure, viz. small-world task, each decision is affected by other \(K\) decisions while it affects a different number of other decisions. This means that under certain task complexity, the influence of the decisions of small-world task varies from one another, though not significantly.
Random task In the random influence matrix, each element is affected randomly by \(K\) other elements, as shown in Figure 2c. However, it remains unknown what these \(K\) elements may exactly be. According to the algorithm proposed by Watts & Strogatz (1998), the random influence matrix is established by exchanging every non-diagonal element in the local matrix with the probability \(\rho = 1\) to other random positions in this row. Therefore, under certain task complexity, the influence of each decision of the task of random structure (random task) differs significantly from that of others. In other words, the random task has some decisions with significant influence.

The crowd component
The crowd refers to those solvers to whom the work is outsourced. After broadcasting a task, we assumed that \(M\) solvers will eventually submit solutions. Thus, the key to characterizing the crowd is to model the solution of each individual in the crowd. Since the solution corresponds to the crowdsourcing task, it is also represented by an N-dimensional vector. Essentially, due to differences in the source of individual competitive advantages, the initial vector representing individual solutions should not be random. For this reason, individual bounded rationality was introduced into crowdsourcing here and its two dimensions were taken into account, namely, bounded rationality level and bounded rationality bias.
Bounded rationality level Simply speaking, faced with a crowdsourcing task, each bounded rationality individual will construct a different cognitive representation smaller than problem space of the task. The dimensions of cognitive representations reflect the degree of bounded rationality, which is called “bounded rationality level” and shortened as \(BRL\). For example, if \(BRL=0.5\), solvers construct cognitive representations on \(N1\) dimensions, hence \(N1=0.5 \ast N\).
To capture the notion that cognitive representation is a simplified real problem space of task, solvers are assumed to have a representation consisting of \(N1\) dimensions, where \(N1<N\). However, it is unknown what constitutes a mapping between this simplified representation and the actual problem space. Following Gavetti & Levinthal (2000), we suppose that the fitness value of each point in the cognitive representation is equal to the average fitness value of the set of points in the actual fitness landscape that are consistent with this point. For a point in the \(N1\) dimensional space, there are \(2N-N1\) points in the actual fitness landscape that are consistent with it. The point in the \(N1\) dimensional space with maximum fitness value is selected to represent cognitive representations. Hence, this cognitive representation is an unbiased estimate of payoff associated with the actual problem space.
Bounded rationality bias The bounded rationality level reflects only the degree of bounded rationality. Nonetheless, a variable, called “bounded rationality bias” (BRB), defined as the extent to which key elements are chosen for cognitive representations, can reflect the accuracy of cognitive representations.
In general, the \(N1\) dimensions of cognitive representations consists of certain key decisions and other randomly chosen ones, in which the number of key decisions is determined by the value of bounded rationality bias. That is to say, the smaller the value of bounded rationality bias, the bigger the number of key decisions, and the higher the accuracy of cognitive representations. Specifically, when the bounded rationality bias is relatively high (e.g. \(BRB = 1\)), solvers will randomly select \(N1\) dimensions from among N dimensions to construct cognitive representations, in which there may be some key decisions that those solvers are not aware of. When the bounded rationality bias is relatively low (e.g. \(BRB=0.6\)), solvers will construct cognitive representations based on \(0.4 \ast N1\) key decisions that are chosen from among \(N\) dimensions and \(0.6 \ast N1\) other decisions chosen randomly from the remaining dimensions after \(0.4 \ast N1\) key decisions have been excluded from \(N\) dimensions.
Key decisions are identified based on the influence of each decision. We argue that the influence of a decision depends on the number of other decisions affected by this decision, as shown in Figure 2. Figure 2 shows that the number of x in each column represents the number of other decisions directly affected by this decision. The greater the number, the greater the influence this decision has and the more likely it is to be identified as a key decision. If several decisions have a similar influence, one of them is chosen randomly as the key decision.
Generally, the bounded rationality bias of professional users is small because they can construct cognitive representations based upon most key decisions and a few other stochastic decisions based on their relevant background knowledge and experience. In contrast, the cognitive representations of ordinary users are based upon most stochastic decisions and a few other key decisions. Consequently, the bounded rationality bias of ordinary users is relatively large.
The process component
In this entity, the focus is on how problem solvers search for and provide solutions to a task. Indeed, the essence of individual solving problem lies in its search for an optimal solution in problem space, which is basically similar to the process known as “adaptive walk” in \(NK\) fitness landscape. Usually, solvers perform a search for new configurations in their neighbourhood by changing their attributes of configurations at every instant. When solvers cannot find a configuration with a higher fitness in their neighbourhood, they halt, since they have reached a local maximum (Levinthal 1997; Rivkin & Siggelkow 2003).
In accordance with the TCPE framework, after an enterprise broadcasts a crowdsourcing task, it withholds comments on individuals’ solutions until the final evaluation. Thus, it is assumed that during the process of individual problem solving, the employers withhold comments on the intermediate version of the solutions formed by any individual, nor will they recommend any staged excellent solution formed by certain individuals to others for reference. Besides, as the problem-solving process of crowdsourcing can be either collaborative or competitive, we focus on the latter, accordingly called “tournament-based crowdsourcing” (Afuah & Tucci 2012), in which solvers submit solutions independently and compete with others. So, in this case, individuals improve their solutions simply by self-innovation rather than imitating other better solutions or learning from employer feedback.
As for self-innovation in the problem solving process, we assume that solvers are myopic and unable to evaluate directly potential solutions that deviate significantly from their status quo solutions, based upon the previous discussion on human decision-making and emulation (Lazer & Friedman 2007). To capture this myopia, we assumed that solvers examine the impact of random change on digit of their status quo solution, and if that potential change brings about an improvement, the solvers may adapt their solutions. Therefore, solvers continue to improve the quality of their solutions based on self-innovation by randomly changing one decision in solutions during the problem-solving process.
The evaluation component
The last point is the evaluation of solutions submitted by solvers, including the quality of individual solutions and crowdsourcing performance emerging from solvers’ continuous search for optimal solutions. Inherently, the quality of solutions can usually be expressed in terms of the payoff of this solution in the fitness landscape. As a result, supposing a decision \(i\) of a solution has the value \(a_i\), its contribution \(c_i\) to the overall payoff of the solution is generated randomly from a continuous uniform distribution ranging from 0 to 1, and depends on both \(a_i\) itself and the value of other \(K\) decisions, represented by the vector \(\mathbf{a_k}\). Hence, the contribution to the payoff of a decision in solution is determined as follows:
| $$\text{Payoff}_i = c_i (a_i, \mathbf{a_k})$$ |
Therefore, the overall payoff of a solution is calculated by averaging the contributions of \(N\) decisions, as follows:
| $$\text{Payoff} = \frac{\sum_{i=1}^N (a_i, \mathbf{a_k})}{N}$$ |
For crowdsourcing performance, Connolly et al. (1990) suggested that the effectiveness of solutions in contests be measured by 1) number of submitted solutions, 2) the quality of solutions and 3) the rarity of solutions. Other suggestions include measuring the amount of attracted solvers (Yang et al. 2009) or solely the quality of the best (winning) solution (Girotra et al. 2010). However, Walter & Back (2011) argued that subjective indicators such as the rarity of solutions and quality of winning solution cannot be used as effective ways to measure crowdsourcing performance, whereas certain objective indicators such as the number and average quality of solutions submitted are more persuasive. Javadi Khasraghi & Aghie (2014) also recommended the average quality of submissions as good proxy measures for crowdsourcing performance as improved solutions will increase crowdsourcing performance and a best solution can be selected. Hence, the crowdsourcing performance (CP) is calculated by the average quality of \(M\) submissions, as follows:
| $$CP = \frac{\sum_{j=1}^M \text{{Payoff}}_j}{M}$$ |
Furthermore, we further measured the diversity of solutions, which reflects the extent to which the solution of any particular solver is different from that of others. From Kim & Rhee (2009), the solution diversity is calculated as:
| $$\text{diversity} = \frac{\sum_{ij}^N H_{ij}}{M \times (M - 1)} $$ |
Experiments and Results
The model simulates the process of solution search conducted by solvers in response to three tasks of different structures, assuming that solvers can integrate a definite set of knowledge components caused by bounded rationality in different configurations to generate their solutions. The model of this manuscript was constructed using Netlogo 5.3. The code is now available at https://www.comses.net/codebases/532b0536-9c02-4857-af05-4f667dd6f878/releases/1.1.0/.
Systematic simulation experiments with different parameter specifications (see Table 1 where default values underlined are) were carried out. Here, we assumed that \(N=12\), as in previous NK research (e.g., Rivkin & Siggelkow 2007; Oyama & Learmonth 2015; Wall 2018). Meanwhile, we set the value of \(K\) at 9 to simulate a high-interaction complex task as a more extreme case, but even if we changed the value of \(K\) (\(K=8\) and \(K=10\)), the findings remain the same. Additionally, we assumed that each simulation generated 100 problem solvers, which reflects the characteristics of large population groups (e.g., Xu et al. 2016; Miller et al. 2006; Kim & Rhee 2009), but even if we changed the number of solvers (\(M=80\) and \(M=120\)), the findings still remained the same.
According to the TCPE framework, the basic simulation process is reproduced below. Faced with a problem or an opportunity, the enterprise selects a task to be crowdsourced, which may be local task, small-world task or random task. The task is then broadcast to the crowd consisting of 100 solvers with different bounded rationality levels and bounded rationality biases, usually in an open call. Next, the crowd members work on the task by examining the impact of randomly changing one digit of their status quo solutions in each period. After some periods, the solvers submit solutions to the problem owner for evaluation. For the final part of the process, the evaluation can be performed by calculating the average quality of 100 solutions. A choice of a best solution is made at the end of the evaluation.
| Parameter | Description | Values |
| \(N\) | Number of task decisions | 12 |
| \(M\) | Number of solvers | 100 |
| \(\rho\) | Rate of exchanging every non-diagonal element to other random position in this row | 0,0.1,0.3,0.5,0.7,0.9,1 |
| \(K\) | Task complexity | 1,5,9 |
| \(BRL\) | Bounded rationality level | 0,0.1,0.3,0.5,0.7 |
| \(BRB\) | Bounded rationality bias | 0,0.1,0.3,0.5,0.7,0.9,1 |
| Crowdsourcing Performance | Average quality of solutions |
After the simulation, we first analysed the effects of the interaction between \(BRL\) and \(\rho\) on crowdsourcing performance in cases where bounded rationality bias was relatively large (\(BRB=1\)), so as to explore the characteristics of the three tasks different in structure and the difference in accomplishing different tasks between individuals with different bounded rationality levels. Based upon this analysis, we proposed a hypothesis that reduced bounded rationality bias helps individuals with different bounded rationality levels to accomplish tasks that vary in structure. In order to verify this hypothesis, two studies were set up. Firstly, we analysed the interaction between \(BRB\) and \(BRL\) on crowdsourcing performance in an attempt to explore the characteristics of the bounded rationality bias, and then verify whether the characteristics were affected by tasks varying in structure. Secondly, we examined the effects of interaction between \(BRL\) and \(\rho\) on crowdsourcing performance under different \(BRB\) so as to verity this hypothesis. Accordingly, this paper set up three sub-models, the parameters of each sub-model shown in Table 2.
Each sub-model with a specific parameter configuration was iterated 100 times with different random seeds to prevent stochastic effects, and 200 periods were run in each experiment. Results were obtained by averaging the last-period objectivity of 100 iterations. We also performed ANOVA and multiple pairwise comparisons, showing that our results were generally statistically significant at a level of 0.05.
| Parameter | Sub-model 1 | Sub-model 2 | Sub-model 3 |
| \(\rho\) | 0,0.1,0.3,0.5,0.7,0.9,1 | 0,0.3,1 | 0,0.3,1 |
| \(K\) | 1,5,9 | 9 | 9 |
| \(BRL\) | 0,0.1,0.3,0.5,0.7 | 0,0.1,0.3,0.5,0.7 | 0,0.1,0.3,0.5,0.7 |
| \(BRB\) | 1 | 0,0.1,0.3,0.5,0.7,0.9,1 | 0.1,0.5,0.9 |
Effects of bounded rationality level and task types
As \(\rho\) is defined as the rate of exchanging every non-diagonal element to other random positions in this row, reflecting the randomness of interaction among task decisions, it can serve as a source to distinguish task types. Figure 3 illustrates the effects of bounded rationality level (\(BRL\)) and \(\rho\) on crowdsourcing performance. The figure indicates that crowdsourcing performance increased gradually as \(BRL\) increased, which is consistent with previous research findings by Gavetti & Levinthal (2000). This is probably because \(BRL\) modelled by cognitive representations in this study, provided a powerful starting point for subsequent efforts, preventing pure problem solvers from being trapped by poor local peaks and also having more potential opportunities when searching for better solutions.
In Figure 3, we can also see that the crowdsourcing performance of local task (\(\rho = 0)\) was better than that of small-world tasks (\(\rho = 0.33)\) and small-world tasks (\(\rho = 0.33)\) were better than random task \((\rho = 1)\), whereas the difference in crowdsourcing performance between the three types of task decreased as BRL increased. To find out the cause of this result, we analysed the characteristics of each type of crowdsourcing task.
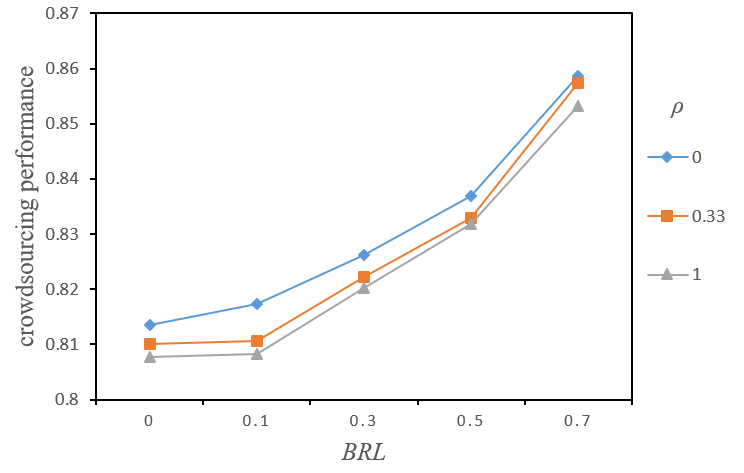
Figure 4 illustrates the effects of task complexity (\(K\)) and \(\rho\) on the average number of local peaks over a sample of 100 independent problem spaces. It shows that the average number of local peaks gradually reduced as \(\rho\) increased, with higher values of \(K\), making this reduction more obvious. Figure 5 illustrates the effects of task complexity (\(K\)) and \(\rho\) on the average payoff of local peaks under similar settings. It does show that there was no significant change in the average payoff of local peaks despite the increase in \(\rho\), implying that task complexity remained unchanged.
In summary, although changes in interaction randomness of task decisions did not affect task complexity, they may have affected the process of task completion. This was probably due to the changes in the number of local peaks caused by the randomness of interaction among task decisions, indicating that the difficulty of transferring from one local peak to another could also change under certain task complexity. Specifically, the more random the interaction, the fewer local peaks, and the greater the difficulty of transferring from one local peak to another.
Based upon this analysis, a possible explanation for the results illustrated in Figure 3 is that under certain task complexity, the randomness of interaction among decisions in random tasks was the largest, local peaks were least, and the difficulty of transferring from one local peak to another was the greatest. Thus, the crowdsourcing performance of random tasks was the least, and local task performance was the greatest. Furthermore, faced with random tasks, solvers who wanted to take advantage of the smaller number of local peaks had to overcome the difficulty of transferring from one local peak to another. The bounded rationality level on the other hand helped solvers overcome this difficulty, given it was the key variable reflecting individuals’ background knowledge. Therefore, the increase in \(BRL\) could gradually reduce differences in crowdsourcing performance among tasks, whereas magnitude relationship remained unchanged, implying that the positive effect of increasing \(BRL\) on overcoming the difficulty of transferring from one local peak to another was limited.
Thus, this paper proposes two ways of improving crowdsourcing performance of non-local tasks (small-world tasks and random tasks). One is to overcome the difficulty of transferring from one local peak to another by improving individual ability, such as improving the accuracy of bounded rationality. The other is to take advantage of the reduction of local peaks, for example, by improving the systematization of bounded rationality. We will consider the effectiveness of the first of these approach by introducing bounded rationality bias, which could improve the accuracy of the cognitive representations.


Effects of bounded rationality level and bounded rationality bias
Figure 6 illustrates the effects of the bounded rationality level (BRL) and bounded rationality bias (\(BRB\)) on crowdsourcing performance under different task types. Figure 6 (a) shows that when ρ = 0, crowdsourcing performance remains intact when \(BRB\) increases and is not affected by BRL. A possible explanation is that since the influence of each decision in local tasks is the same as others, all solvers will construct cognitive representations based on randomly chosen decisions regardless of \(BRB\), and so \(BRB\) has no effect.
However, Figure 6 (b) and Figure 6 (c) show that when \(\rho\) equals 0.33 and 1 respectively, crowdsourcing performance decreased gradually as \(BRB\) increased, except when the \(BRL\) is very low (\(BRL = 0\)). In other words, \(BRB\) had a negative effect on crowdsourcing performance of non-local tasks (small-world tasks and random tasks) and was affected by \(BRL\). As a result, the higher the \(BRL\), the greater the negative effect was. In addition, comparing Figure 6 (b) with Figure 6 (c), we can see that the negative effect of \(BRB\) on the crowdsourcing performance of non-local tasks was also affected by \(\rho\). The higher the \(\rho\) value, the greater the negative effect of \(BRB\). To explain the negative effect of the \(BRB\), the property of \(BRB\) was further analysed.
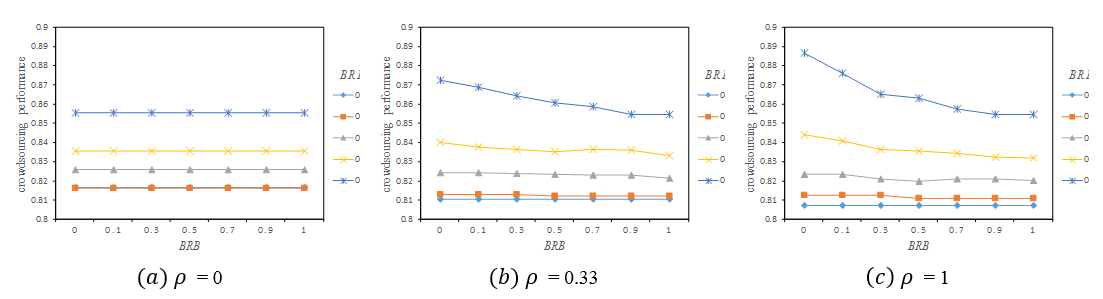
Figure 7 (b) illustrates the effect of \(BRB\) on crowdsourcing performance and diversity of solutions with \(BRL=0.7\) and \(rho= 1\) when period \(= 0\). Here, we can see that the initial crowdsourcing performance decreased gradually as \(BRB\) increased, while the diversity of solutions increased gradually, indicating that \(BRB\) had dual effects: (1) negatively affecting the initial crowdsourcing performance, determining the starting point of searching for solutions, and (2) positively affecting the diversity of solutions, providing more potential for long term searches. That is to say, if solvers can identify more key task decisions to construct cognitive representations, the initial crowdsourcing performance would be relatively high. However, the diversity of solutions would also be relatively low because the solvers’ cognitive representations built around key decisions are relatively similar to each other.

Although \(BRB\) had both positive and negative effects, why did it eventually become negative? To find out why, we further analysed the evolution process of the diversity of solutions (as shown in Figure 8) and the crowdsourcing performance (as shown in Figure 9) under different \(BRB\). In Figures 8 and 9, we can see that the diversity of solutions in low \(BRB\) was always lower than that in relatively high \(BRB\) with more experimental periods, while crowdsourcing performance results were the opposite. In other words, although the diversity of solutions was lower when \(BRB\) was low, the starting point was better. More importantly, the diversity of solutions presented an apparent inverted U-shaped trend of change with more experimental periods, which may essentially lead to higher crowdsourcing performance. Indeed, the changing trend of solution diversity was the "transient diversity" process mentioned previously (Zollman 2010). This "transient diversity" refers to the longer time needed to solve problems when searching for better solutions by relying on diversity, ultimately resulting in convergence and yielding consensus (Zollman 2010).
In summary, an important finding of this study is that solution diversity by destroying the quality of initial solutions through increasing bounded rationality bias cannot guarantee that initial crowdsourcing performance is achieved or exceeded after a long-term process of exploiting diversity. Consequently, bounded rationality bias has negative effects.


Effects of bounded rationality level and task types under different bounded rationality biases
We hypothesized that the improvement of individual ability may increase crowdsourcing performance of non-local tasks, this section now discusses whether reducing bounded rationality bias can also improve crowdsourcing performance. Figure 10 illustrates the effects of bounded rationality level (\(BRL\)) and \(\rho\) on crowdsourcing performance under different bounded rationality biases (\(BRB\)).
Comparing Figure 10 (a), (b) and (c), we can see that when \(BRL\) is relatively low (\(BRL < 0.3\)), crowdsourcing performance of all tasks varies little with decreased \(BRB\), whereas local tasks always performed best, followed by small-world task and then random task. This is because the negative effect of \(BRB\) is too small a low \(BRL\). That is, reducing \(BRB\) does not significantly improve individual ability if \(BRL\) is relatively low.
However, in the case of high \(BRL\) (\(BRL > 0.3\)), the magnitude relationship of crowdsourcing performance of all tasks, gradually diverged with a clear gap between them as \(BRB\) decreases. Interestingly, results were opposite those of low \(BRL\). In other words, random tasks performed best, followed by small-world task and then local task. This is because the negative effect of the \(BRB\) on crowdsourcing performance accentuates with increased BRL. Thus, reducing \(BRB\) can significantly improve individual ability, eventually improving crowdsourcing performance.
In summary, reduced bounded rationality bias cannot significantly improve crowdsourcing performance of non-local tasks when bounded rationality level is relatively low. In this case, local tasks performed best and random task performs worst. However, when the bounded rationality level was relatively high, the reduction in bounded rationality bias does not only significantly improve crowdsourcing performance of non-local tasks but also changes the magnitude relationship of crowdsourcing performance of all tasks. Consequently, random task performed best and local task performed worst.

Discussion
By constructing an agent-based simulation model based on NK fitness landscapes and TCPE framework to simulate the problem-solving process of crowdsourcing, we used a series of simulations to examine the effects of task structure and individual bounded rationality on crowdsourcing performance. Our results showed that the more random the interaction among task decisions were, the lower the crowdsourcing performance was. Thus, random tasks were the most complicated while local tasks were the simplest. Meanwhile, bounded rationality bias was negatively correlated with crowdsourcing performance, depending on the bounded rationality level and interaction structure of the task decisions. The higher the bounded rationality level and more random the interaction structure of task decisions, the greater the negative impact of bounded rationality bias. Furthermore, when bounded rationality level was low, regardless of the bounded rationality bias, local tasks always performed best and random tasks worst. However, when the bounded rationality level was high, if bounded rationality bias was also high, local tasks always performed best and random tasks performed worst; if bounded rationality bias was moderate, random tasks performed best, followed by small-world tasks and then local tasks, but the gap in crowdsourcing performance between three tasks was not obvious; if bounded rationality bias was low, random tasks performed best, followed by small-world task and then local tasks, and there was a significant gap between the three tasks in crowdsourcing performance.
The theoretical contributions of this study can be summed up as follows.
Methodological Innovation
So far, quantitative crowdsourcing research has mostly been based on empirical and mathematical statistical methods. However, it is difficult for these methods to describe the dynamic process of crowdsourcing problem solving from a systemic and holistic perspective. This has created a lack of adequate explanations for the entire crowdsourcing problem-solving process. In essence, problem solving is a complicated, multi-level and recursive process. Some academics believe that this problem can be verified by using simulation modelling (Harrison et al. 2007; Davis et al. 2007). The simulation method based on complex adaptive system theory can take into account various factors in problem solving processes and explain the validity and conflicts of the relationship of various factors, providing a more comprehensive perspective. However, most crowdsourcing simulation studies, simply adopt classical models, such as the NK model (e.g., Afuah & Tucci 2012; Vuculescu & Bergenholtz 2014), the genetic algorithm model (Vuculescu & Bergenholtz 2014), etc., whereas only a few authors have tried to construct a simulation model that realistically represent crowdsourcing problem solving.
Here, by comparing frameworks of crowdsourcing processes, the TCEP framework was combined with the NK model to construct a model that simulated crowdsourcing problem solving. It thus overcomes the shortcomings of existing research and provides a novel methodology for follow-up crowdsourcing simulation research.
Deepening the understanding of the formation of task complexity
For a long time, despite simulation literature of collective problems solving regarding complexity as an important factor (e.g., Lazer & Friedman 2007; Fang et al. 2010), there has been little work on the formation of task complexity. Indeed, March & Simon (1958) described the essential characteristics of task complexity as early as 1958 and indicated that task complexity is reflected not only in the multiplicity of “path to goal”, but also in a series of the possible complicated internal relationships among non-independent subtasks. Later, Rivkin & Siggelkow (2003) described internal relationships in the NK model, in which each sub-task is affected by other \(K\) sub-tasks and the value of \(K\) represented task complexity. In reality, the internal relationships among sub-tasks are much more complicated than those previously described. In this study, we believe that the number of sub-tasks affected by a subtask could vary, whenever \(K\) is fixed. However, it remains to be seen whether this difference has an impact on task complexity. In an attempt to bridge this gap, without affecting overall complexity of the task, the internal structure does affect ultimate crowdsourcing performance. Moreover, we argue that the complexity of a task depends on two aspects, viz. 1) the number of local peaks in the problem space of task and 2) the difficulty of transferring from one local peak to another. With the increase in interaction randomness among task decisions, the number of the local peaks in task problem space decreases and the difficulty of transferring from one peak to another increases. However, the overall complexity of the task remains, providing a better explanation of the inherent reasons of task complexity.
Enriching the insight into diversity
Previous research on collective problem solving and organizational learning reported that diversity is more important than the initial ability in improving long-term adaptability of a group (e.g., March 1991; Miller et al. 2006). One thing that all these studies have in common is that their research object is a learning group. That is, there is horizontal learning (learning among individuals) or longitudinal learning (learning between individuals and organizations) in the group. However, as this paper is focused on tournament-based crowdsourcing, a quite different conclusion is reached. Bounded rationality bias can affect crowdsourcing performance in two ways, viz. 1) impact on the initial quality of solutions and 2) impact on the initial diversity of solutions. However, the initial diversity of solutions, obtained by destroying the quality of initial solutions with increased bounded rationality bias, cannot guarantee success after a long period of exploration and exploitation. Thus, initial quality of solutions is more important than initial diversity of solutions. Indeed, the effective use of diversity is the key to improving crowdsourcing performance.
Finding the matching relationship between task types and solver types
Our major contribution lies in the fact that we have elaborated matching relationships between task types and solver types by exploring the effects of task structure and individual bounded rationality on crowdsourcing performance. Since tasks act as connection between contractors, platforms and participants (Rouse 2010), they will affect the choice of mode and solver types. There have been studies on the effect of task types on this selection. For example, Nakatsu et al. (2014) summarized seven task situations based on three dimensions of task complexity and identified which mode was the most suitable for a particular task situation.
However, due to the scarcity of literature on interactive relationships between task and participant characteristics, it remains to be seen how task types are related to and matched with solver types. This study is an effort to answer this question. The matching relationship between task types and solver types is described as follows. In emerging industries, where the bounded rationality level of solvers is generally low, for all solvers, local task always performs best and random task always performs worst. However, in traditional industries where the bounded rationality level of solvers is generally high, when solvers are ordinary users, local tasks perform best, followed by small-world tasks and then random tasks. When solvers are more expert, random tasks perform best, followed by small-world and then local tasks, but with little significant gap between them. Finally, when solvers are professional, random tasks perform best, followed by small-world and then local tasks, with however a significant gap between them.
Implications
As it provides a theoretical basis for enterprises to design a screening crowdsourcing mechanism to recruit the right solvers for the right task, this study does have some practical significance. Specifically, since the emerging industry is still in a fledging stage, taking virtual reality (VR) for example, there has been constant exploration and development in every aspect of it. Thus, solvers have relatively little knowledge about the industry. In comparison, in developed traditional industries such as construction, solvers in these industries have acquired more relevant knowledge. Therefore, bounded rationality level can be employed as an important variable to differentiate these industries. Furthermore, since the bounded rationality bias of professional users is lower than ordinary users, it can be used to differentiate these users. According to the principle of cost minimization in solvers recruitment, enterprises have to first identify the type of their industry, and then design a screening mechanism based on the matching relationship between the task types and solver types. Accordingly, whatever the type of task may be in emerging industries, recruiting ordinary users could adequately meet the needs of the task. On the other hand, for traditional industries, it would be wiser to recruit solvers based on task types. When an enterprise has a local task to accomplish, recruiting ordinary users should normally be enough for the task. When an enterprise has a small-world task, it should recruit more expert individuals. When an enterprise has a random task, professional users should be recruited.
Our paper also provides a theoretical tool to shed light on simulating the process of problem solving in crowdsourcing. Further research could extend the basic model constructed here by including more complicated factors. For example, this paper did not consider interaction behaviour among solvers due to the tournament-based approach. Secondly, personnel turnover, which is a major concern of previous organizational learning research, is also an important feature of many online crowdsourcing communities. This continuously changes solver compositions of crowdsourcing and introduces new solutions. Therefore, exploring the effect of turnover could help us understand the problem-solving process in a dynamic group. Thirdly, we assumed that the employer does not provide true feedback to problem-solvers during the problem-solving process. According to the literature on organizational learning, feedback does have an impact on organization performance. Similarly, true feedback provided by the employer may also impact crowdsourcing performance. Therefore, further studies could consider this aspect by exploring the effects of feedback, such as an optimal solution selected from temporary solutions or a solution synthesized by selecting several better solutions.
Acknowledgements
We acknowledge the support of the National Social Science Foundation of China (Grant No.15XGL001). Besides, the authors gratefully acknowledge the valuable comments and helpful suggestions of the JASSS reviewers.References
ABDOLMOHAMMADI, M. J. (1999). A comprehensive taxonomy of audit task structure, professional rank and decision aids for behavioral research. Behavioral Research in Accounting, 11, 51.
AFUAH, A., & Tucci, C. L. (2012). Crowdsourcing as a solution to distant search. Academy of Management Review, 37(3), 355-375.
BRABHAM, D. C. (2008). Crowdsourcing as a model for problem solving: An introduction and cases. Convergence, 14(1), 75–90. [doi:10.1177/1354856507084420]
BRABHAM, D. C. (2012). A model for leveraging online communities. In A. Delwiche & J. Henderson (Eds.), The Participatory Cultures Handbook. New York, NY: Routledge.
CHI, M. T., Feltovich, P. J., & Glaser, R. (1981). Categorization and representation of physics problems by experts and novices. Cognitive Science, 5(2), 121-152. [doi:10.1207/s15516709cog0502_2]
CHIU, C. M., Liang, T. P., & Turban, E. (2014). What can crowdsourcing do for decision support? Decision Support Systems, 65(C), 40–49.
CONNOLLY, T., Jessup, L. M. & Valacich, J. S. (1990). Effects of anonymity and evaluative tone on idea generation in computer-mediated groups. Management Science, 36(6), 689–703. [doi:10.1287/mnsc.36.6.689]
DAVIS, J. P., Eisenhardt, K. M., & Bingham, C. B. (2007). Developing theory through simulation methods. Academy of Management Review, 32(2), 480-499.
DE KLEER, J. (1990). Multiple representations of knowledge in a mechanics problem-solver. In D. S. Weld & J. de Kleer (Eds.), Readings in Qualitative Reasoning about Physical Systems. Amsterdam: Elsevier, pp. 40-45. [doi:10.1016/B978-1-4832-1447-4.50009-2]
DENNIS, A. R., Aronson, J. E., Heninger, W. G., & Walker, E. D. (1999). Structuring time and task in electronic brainstorming. MIS Quarterly, 23(1), 95-108.
EICKHOFF, C., & Vries, A. P. De. (2011). How crowdsourcable is your task. In Proceedings of the Workshop on Crowdsourcing for Search and Data Mining (CSDM) at the Fourth ACM International Conference on Web Search and Data Mining (WSDM), (pp. 11–14).
FANG, C., Lee, J., & Schilling, M. A. (2010). Balancing exploration and exploitation through structural design: The isolation of subgroups and organizational learning. Organization Science, 21(3), 625-642. [doi:10.1287/orsc.1090.0468]
FREI, B. (2009). Paid Crowdsourcing. Micro, (pp. 1–17).
GAVETTI, G., & Levinthal, D. (2000). Looking forward and looking backward: Cognitive and experiential search. Administrative Science Quarterly, 45(1), 113-137.
GILOVICH, T., Griffin, D., & Kahneman, D. (2002). Heuristics and Biases: The Psychology of Intuitive Judgment. Cambridge: Cambridge University Press. [doi:10.1017/CBO9780511808098]
GIROTRA, K., Terwiesch, C., & Ulrich, K. T. (2010). Idea generation and the quality of the best idea. Management Science, 56(4), 591-605.
HARRISON, J. R., Lin, Z., Carroll, G. R., & Carley, K. M. (2007). Simulation modeling in organizational and management research. Academy of Management Review, 32(4), 1229-1245. [doi:10.5465/amr.2007.26586485]
HOWE, J. (2006). The Rise of Crowdsourcing. Wired Magazine, 14(06), 1–4.
JAVADI Khasraghi, H., & Aghaie, A. (2014). Crowdsourcing contests: understanding the effect of competitors’ participation history on their performance. Behaviour & Information Technology, 33(12), 1383-1395. [doi:10.1080/0144929X.2014.883551]
JIAN-GANG, P. A. N. G. (2015). The Risk Management Mechanism of Crowdsourcing Community Innovation. China Soft Science, 2, 019.
JOSEPH, G. M., & Patel, V. L. (1990). Domain knowledge and hypothesis generation in diagnostic reasoning. Medical Decision Making, 10(1), 31-44. [doi:10.1177/0272989X9001000107]
KANNANGARA, S. N., & Uguccioni, P. (2013). Risk management in crowdsourcing-based business ecosystems. Technology Innovation Management Review, 3(12), 32.
KASTHURIRATHNA, D., Piraveenan, M., & Uddin, S. (2016). Modeling networked systems using the topologically distributed bounded rationality framework. Complexity, 21(S2), 123-137. [doi:10.1002/cplx.21789]
KAUFFMAN, S. (1993). The Origins of Order. Self-Organization and Selection in Evolution. New York, NY: Oxford University Press.
KAUFFMAN, S. & Levin, S. (1987). Towards a general theory of adaptive walks on rugged landscapes. Journal of Theoretical Biology, 128(1), 11–45.
KIM, T., & Rhee, M. (2009). Exploration and exploitation: Internal variety and environmental dynamism. Strategic Organization, 7(1), 11-41. [doi:10.1177/1476127008100125]
LAZER, D., & Friedman, A. (2007). The network structure of exploration and exploitation. Administrative Science Quarterly, 52(4), 667-694.
LEVINTHAL, D. A. (1997). Adaptation on Rugged Landscapes. Management Science, 43(7), 934–950. [doi:10.1287/mnsc.43.7.934]
LEVINTHAL, D., & March, J. G. (1981). A model of adaptive organizational search. Journal of Economic Behavior & Organization, 2(4), 307-333.
MARCH, J. G. (1991). Exploration and exploitation in organizational learning. Organization Science, 2(1), 71-87. [doi:10.1287/orsc.2.1.71]
MARCH, J. G., & Simon, H. A. (1958). Organizations. Oxford: Wiley.
MILLER, K. D., Zhao, M., & Calantone, R. J. (2006). Adding interpersonal learning and tacit knowledge to March's exploration-exploitation model. Academy of Management Journal, 49(4), 709-722.
NAKATSU, R. T., Grossman, E. B., & Iacovou, C. L. (2014). A taxonomy of crowdsourcing based on task complexity. Journal of Information Science, 40(6), 823-834. [doi:10.1177/0165551514550140]
NATALICCHIO, A., Petruzzelli, A. M., & Garavelli, A. C. (2017). Innovation problems and search for solutions in crowdsourcing platforms – a simulation approach. Technovation, 64, 28-42.
OREG, S., & Bayazit, M. (2009). Prone to bias: Development of a bias taxonomy from an individual differences perspective. Review of General Psychology, 13(3), 175. [doi:10.1037/a0015656]
ORGANISCIAK, P. (2010). Why bother? Examining the motivations of users in large-scale crowd-powered online initiatives (Doctoral dissertation, University of Alberta).
OYAMA, K., Learmonth, G., & Chao, R. (2015). Applying complexity science to new product development: modeling considerations, extensions, and implications. Journal of Engineering and Technology Management, 35, 1-24. [doi:10.1016/j.jengtecman.2014.07.003]
RANDEL, J. M., Pugh, H. L., & Reed, S. K. (1996). Differences in expert and novice situation awareness in naturalistic decision making. International Journal of Human-Computer Studies, 45(5), 579-597.
RIVKIN, J. W., & Siggelkow, N. (2003). Balancing search and stability: Interdependencies among elements of organizational design. Management Science, 49(3), 290-311. [doi:10.1287/mnsc.49.3.290.12740]
RIVKIN, J. W., & Siggelkow, N. (2007). Patterned interactions in complex systems: Implications for exploration. Management Science, 53(7), 1068-1085.
ROUSE, A. C. (2010). A preliminary taxonomy of crowdsourcing. ACIS 2010 Proceedings, 76, 1-10.
ROWE, R. M., & McKenna, F. P. (2001). Skilled anticipation in real-world tasks: Measurement of attentional demands in the domain of tennis. Journal of Experimental Psychology: Applied, 7(1), 60.
SÁNCHEZ-MANZANARES, M., Rico, R., & Gil, F. (2008). Designing organizations: Does expertise matter? Journal of Business and Psychology, 23(3-4), 87-101. [doi:10.1007/s10869-008-9076-y]
SCHENK, E., & Guittard, C. (2011). Towards a characterization of crowdsourcing practices. Journal of Innovation Economics, 7(1), 93.
SHAFIR, E., & LeBoeuf, R. A. (2002). Rationality. Annual review of psychology, 53(1), 491-517. [doi:10.1146/annurev.psych.53.100901.135213]
SIGGELKOW, N., & Levinthal, D. A. (2003). Temporarily divide to conquer: Centralized, decentralized, and reintegrated organizational approaches to exploration and adaptation. Organization Science, 14(6), 650-669.
SIMON, H. A. (1955). On a class of skew distribution functions. Biometrika, 42(3/4), 425–440, [doi:10.2307/2333389]
SIMON, H. A. (1973). The structure of ill structured problems. Artificial Intelligence, 4(3-4), 181-201.
SOLOW, D., Burnetas, A., Tsai, M.-C. & Greenspan, N. S. (1999). Understanding and attenuating the complexity catastrophe in Kauffam’s NK model of genome evolution. Complexity, 5(1), 53–66. [doi:10.1002/(SICI)1099-0526(199909/10)5:1<53::AID-CPLX9>3.0.CO;2-W]
STEWARD, D. V. (1981). The design structure system: A method for managing the design of complex systems. IEEE Transactions on Engineering Management, (3), 71-74.
VUCULESCU, O., & Bergenholtz, C. (2014). How to solve problems with crowds: a computer-based simulation model. Creativity and Innovation Management, 23(2), 121-136. [doi:10.1111/caim.12059]
WALL, F. (2018). Emergence of task formation in organizations: Balancing units' competence and capacity. Journal of Artificial Societies & Social Simulation, 21(2), 6: https://www.jasss.org/21/2/6.html. [doi:10.18564/jasss.3679]
WALTER, T., & Back, A. (2011). Towards measuring crowdsourcing success: An empirical study on effects of external factors in online idea contest. Retrieved from https://www.alexandria.unisg.ch/214388/1/MCIS_ Walter_Back_2011.pdf
WATTS, D. J., & Strogatz, S. H. (1998). Collective dynamics of ‘small-world’ networks. Nature, 393(6684), 440.
WINTER, S. G., Cattani, G., & Dorsch, A. (2007). The value of moderate obsession: Insights from a new model of organizational search. Organization Science, 18(3), 403-419. [doi:10.1287/orsc.1070.0273]
WRIGHT, S. (1931). Evolution in Mendelian populations. Genetics, 16(2), 97-159.
WRIGHT, S. (1932). The roles of mutation, inbreeding, crossbreeding, and selection in evolution. In Proceedings of the Sixth International Congress of Genetics.
XU, B., Liu, R., & He, Z. (2016). Individual irrationality, network structure, and collective intelligence: An agent-based simulation approach. Complexity, 21(S1), 44-54.
YANG, Y., Chen, P. Y., & Pavlou, P. (2009). Open innovation: An empirical study of online contests. In ICIS 2009 Proceedings, 13.
ZOLLMAN, K. J. S. (2010). The epistemic benefit of transient diversity. Erkenntnis, 72(1), 17-35.
