Introduction
Reproducibility of results is crucial to all scientific disciplines (Giles 2006), a fundamental scientific principle, and a hallmark of cumulative science (Axelrod 1997). The reproducibility of simulation experiments has gained attention with the increasing application of computational methods over the past two decades (Stodden et al. 2016). Simulation models can be verified by reproducing identical or at least similar results. Moreover, replicated models allow to conduct further research on a reliable basis. Still, as in other scientific endeavors (Nosek et al. 2015), independent replications of simulation studies are lacking (Heath et al. 2009; Janssen 2017).
Potential reasons for the shortage of independent model replications are manifold: lacking incentives for researchers, deficient communication of model information, uncertainty in how to validate replicated results, and the inherent difficulty of re-implementing (prototype) models (Fachada et al. 2017)[1]. Agent-based models, moreover, are built on more assumptions than traditional models due to their high degree of disaggregation and bottom-up logic, rendering more difficult the verification and validation of these models (Zhong & Kim 2010). Replication efforts of agent-based models may also lack supporting methods.
This paper shows how replicated simulation models can be used to develop theory, which could increase the incentives to publish replicated work. Both replication and the subsequent theory development are fostered here through the use of simulation standards, such as the ODD (Overview, Design concepts, and Details) protocol and DOE (design of experiments) principles; these standards were not used when the model we replicate was initially developed, presented, and analyzed. For this exercise, we use the agent-based simulation model of organizational routines by Miller et al. (2012), examining the relationship between different types of individual memory and organizational routines. Although 158 publications to date have cited this study, none so far have replicated the model.
We selected this model for our replication study for several further reasons. First, the model is highly original in its approach to address the micro-foundations of organizational routines by modeling agents’ procedural, declarative, and transactive memory,[2] enabling an investigation of the dynamic relationship between individual cognitive properties and both the formation and the performance of organizational routines. Second, it is currently one of the most frequently cited agent-based models of organizational routines.[3] Third, it was published in the reputed Journal of Management Studies, not a typical outlet for agent-based simulation studies. Finally, it has the potential to support further development of theory, and the fact that it did not use simulation standards enables us to demonstrate their potential benefits.
This paper proceeds in three main steps in order to show how a replicated simulation model can be used both to generalize previous results and to refine theory: (1) replicate and verify the model, comparing results with those of Miller et al. (2012);[4] (2) test the usefulness of agent-based modeling standards for replication, such as the ODD protocol and DOE principles; and (3) develop theoretical understanding of the modeled organizational system by extending the simulation experiments on verified grounds.
We successfully reproduce the results of Miller et al. (2012) in the replicated model. The ODD structure helps to systematically extract information from the original model, while DOE principles guide the experimental analysis of the model and enhance interpretability of the results. For example, we clarify one ambiguous model assumption. For theory development, we generalize the scope of the replicated model by investigating how additional scenarios, such as a merger or a volatile environment, affect routine formation and performance, as well as relating previous and new findings to prominent constructs in the literature.
The remainder of this paper is structured as follows. The next section reviews relevant literature concerning replication, simulation standards, and theory development. We then introduce our replication methodology, where we apply the ODD protocol and DOE principles in the context of the simulation model replication. The replicated model is then used to generalize and refine previous theoretical insights. The final section concludes and provides an outlook for further research.
Related Literature
Replication, in general, is considered a cornerstone of good science. The successful replication of results powerfully fosters the credibility of a study. Besides, replications can be used to advance the knowledge in a field, in the sense that the original study design can be extended, generalized, and applied in new domains. Replications allow linking existing and new knowledge (Schmidt 2009) and reflect an ideal of science as an incremental process of cumulative knowledge production that avoids “reinventing the wheel”(Richardson 2017).
Computational models successfully replicated by independent researchers are considered to be more reliable (Sansores & Pavón 2005) and credible (Zhong & Kim 2010). Replications can reveal three types of errors: (1) programming errors; (2) misrepresentations of what was actually simulated; and (3) errors in the analysis of simulation results (Axelrod 1997; Sansores & Pavón 2005). A replication might also reveal hidden, undocumented, or ambiguous assumptions (Miodownik et al. 2010), which can affect the fit of the implemented model with the world to be represented.
The current practice stands in stark contrast to the often-stated importance of replication. Nosek et al. (2015) sparked intense discussion of a potential “replication crisis” in fields as diverse as psychology, economics, and medicine. While much of this discussion concerned empirical areas, replicability and replication also have high relevance for computational modeling (Miłkowski et al. 2018; Monks et al. 2019). Nevertheless, most agent- based models have not been replicated (Heath et al. 2009; Legendi & Gulyas 2012; Rand & Wilensky 2006).[5] Most researchers build new models instead of using existing models (Donkin et al. 2017; Thiele & Grimm 2015), a practice which hampers cumulative and collective learning and raises the costs of modeling (Dawid et al. 2019; Monks et al. 2019). [6] Replicated models can also provide a good starting point for theory development (Lorscheid et al. 2019).
Recently developed standards and guidelines to enable rigorous simulation modeling and model analysis (Grimm et al. 2010; Lorscheid et al. 2012; Rand & Rust 2011; Richiardi et al. 2006) can also support the replication process. Social simulation researchers increasingly acknowledge such standards as the ODD protocol and DOE principles (Hauke et al. 2017). The ODD protocol allows the standardized communication of models (Grimm et al. 2006, Grimm et al. 2010), while DOE principles can foster the systematic analysis and communication of model behavior (Lorscheid et al. 2012; Padhi et al. 2013). Using these standards can help researchers compare simulation models, designs, and results.
Given the cumulative nature of science, replication, ideally supported by these standards, can potentially help to build theory through simulation. Among the many ways to develop theory (see Lorscheid et al. 2019), we focus here on the ideas of Davis et al. (2007),[7] who position the elaboration of simple theories via simulation experiments in a “sweet spot” between theory-creating research, formal modeling, and empirical, theory-testing research. Basic or simple theory[8] typically stems from individual cases or formal modeling; the authors describe it as follows:
By simple theory, we mean undeveloped theory that has only a few constructs and related propositions with modest empirical or analytic grounding such that the propositions are in all likelihood correct but are currently limited by weak conceptualization of constructs, few propositions linking these constructs together, and/or rough underlying theoretical logic. Simple theory also includes basic processes that may be known (e.g., competition, imitation) but that have interactions that are only vaguely understood, if at all. Thus, simple theory contrasts with well-developed theory, such as institutional and transaction cost theories that have multiple and clearly defined theoretical constructs (e.g., normative structures, mimetic diffusion, asset specificity, uncertainty), well-established theoretical propositions that have received extensive empirical grounding, and well-elaborated theoretical logic. Simple theory also contrasts with situations where there is no real theoretical understanding of the phenomena. (Davis et al. 2007, p. 482)
In this spirit, we later contribute to the literature on dynamic capabilities, [9] specifically from the perspective of knowledge integration. Despite a large body of research, the concept of dynamic capabilities has not reached the level of elaboration of other theories in the field of strategic management or organizational science (Helfat & Peteraf 2009; Pisano 2015). This is perhaps because the concept has a longitudinal and processual focus and because empirical data are difficult to obtain; all these factors make simulation particularly useful for theory development (Davis et al. 2007).
In this regard, we posit that simulations can strengthen the formal understanding of knowledge-integrating processes as one potential micro-foundation for dynamic capabilities. To this end, we begin with a replicated model of Miller et al. (2012), who acknowledge their study’s contribution to the literature on dynamic capabilities, and then conduct several additional simulation experiments. We focus on the representation of underlying knowledge structures as a determinant for the effectiveness of dynamic capabilities. We use formal modeling to increase precision, compared to previously used verbal models (Smaldino et al. 2015), in the underlying theoretical logic and the description of the connected constructs. In doing so, we refine the theory of dynamic capabilities by expressing knowledge-integrating processes as a potential mechanism affecting knowledge structures’ underlying routines. Hence, we aim to strengthen the conceptualization of constructs. At the same time, we generalize the concept of knowledge structures in routines’ formation by showing the benefits of this concept in new contexts, such as mergers.
Method
The replication re-implements the conceptual model in a different software and hardware environment to ensure that neither hardware nor software specifics drive results (Miodownik et al. 2010; Wilensky & Rand 2007). Greater differences in the implementation yield stronger verification if the model nevertheless produces the same results.
Table 1 compares the features of the original study and our replication. The replication is performed by independent researchers, which enhances the objectivity. The conceptual model is re-implemented in a different software environment, which allows the detection of coding issues and effects induced by different stochastic algorithms. We chose NetLogo for re-implementation, a widely-used agent-based simulation software package (Hauke et al. 2017; Rand & Rust 2011). A significant difference between the original model implementation and our re-implementation is that we apply the relatively recently established modeling standards of ODD and DOE. This enables us to uncover potential ambiguities hampering a fully conclusive replication process, necessitating the exploration of implicitly made assumptions.
| Dimension | Original study | Replication |
| Year | 2012 (published) | 2020 |
| Authors | Miller, Pentland, Choi | Hauke, Achter, Meyer |
| Simulation sohware | MATLAB 7 | NetLogo 6.0 |
| Model documentation | individual structure | ODD protocol |
| Model analysis | selected experiments | selected experiments + DOE |
The replication aims to reproduce the output pattern of the original model (Grimm et al. 2005) as a criterion of success (Wilensky & Rand 2007). We further evaluate our replication according to the three-tier classification of Axelrod (Axelrod 1997):
- The re-implemented model generates identical results to the original model. Such “numerical identity” is only possible with a model having no stochastic elements or using the same random number generator and seeds.
- The results of the re-implemented model do not statistically deviate from the original; they are “distributionally equivalent,” which is sufficient for most purposes.
- The results of the re-implemented model show “relational equivalence” to the results produced by the original model. This weakest level refers to models with approximately similar internal relationships among their results. For example, output functions may have comparable gradients but deviate statistically (e.g., differing coefficients of determination).
Additional DOE analysis (see Appendix C) allows examination “under the hood” of a simulation result. Opening the typically “black box” of simulation results allows systematic verification and validation, further increasing the credibility of the replication. [10] Based on the replicated model, we perform additional experiments to complement and extend the results of Miller et al. (2012), thereby developing a deeper understanding of routines by analyzing agents’ knowledge base and developing a broader understanding by modeling merging organizations and organizations operating in volatile environments.
Model Description
A condensed model description follows below (for a full description, see the ODD protocol in Appendix A). [11] The model aims to show how cognitive properties of individuals and their distinct forms of memory affect the formation and performance of organizational routines in environments characterized both by stability and by crisis (see also Miller et al. 2012).
Table 2 overviews the model parameters. Agents represent human individuals; together, they form an organization. By default, the organization comprises \(n\) agents. The organization must handle problems that it faces from its environment. A problem consists of a sequence of \(k\) different tasks (Miller et al. 2012).
| Variable | Description | Value (Default) |
| \(n\) | Number of agents in the organization | 10, 30, 50 |
| \(k\) | Number of different tasks in a problem | 10 |
| \(a\) | Task awareness of an agent | 1, 5, 10 |
| \(p_t\) | Probability that an agent updates its transactive memory | 0.25, 0.5, 0.75, 1.00 |
| \(p_d\) | Probability that an agent updates its declarative memory | 0.25, 0.5, 0.75, 1.00 |
| \(w_d\) | Declarative memory capacity of an agent | 1, 25, 50 |
Agents have different skills, though skills themselves are not varied. Each agent has the skill to perform a particular task (Miller et al. 2012). The number of agents equals at least the number of different tasks in a problem, thus ensuring that the organization is always capable of solving a problem. The number of agents can exceed the number of tasks tasks (\(n > k\)), according to the parameter ranges (Miller et al. 2012). The \(k\) different skills are assumed to be distributed uniformly among the agents.[12]
Any agent is aware of a number a of randomly assigned tasks, and each agent is at least aware of the task the agent is skilled for (Miller et al. 2012). Agents can recognize tasks of which they are aware and are blind to unfamiliar tasks (Miller et al. 2012). Each agent is aware of a limited number of tasks in any problem (\(1 \leq a \leq k\)).
Agents have a chance to memorize a subsequent task \(w_d\) in their declarative memory once they have performed a task and handed the problem over to another agent, who then accomplishes the next task. An agent memorizes a task with a certain probability given by the variable \(p_d\). Additionally, agents can memorize the skills of other agents in their transactive memory. The number of agents and their skills which each agent can memorize is limited by the number of agents in the organization. By default, the probability \(p_t\) is 0.5 that an agent will add an entry to transactive memory (Miller et al. 2012).
Agents are distributed across the organization. Scale and distance are not modeled explicitly, but time is crucial. First, operationally, each organizational problem-solving process is time-consuming. Second, strategically, an organization that consecutively solves problems might form routines over time.
Organizations have to perform the tasks in a given order to solve a problem. Once each task is performed, the problem is solved (Miller et al. 2012). The organization copes with several problems over time, whether recurring or changing in terms of the task sequence.
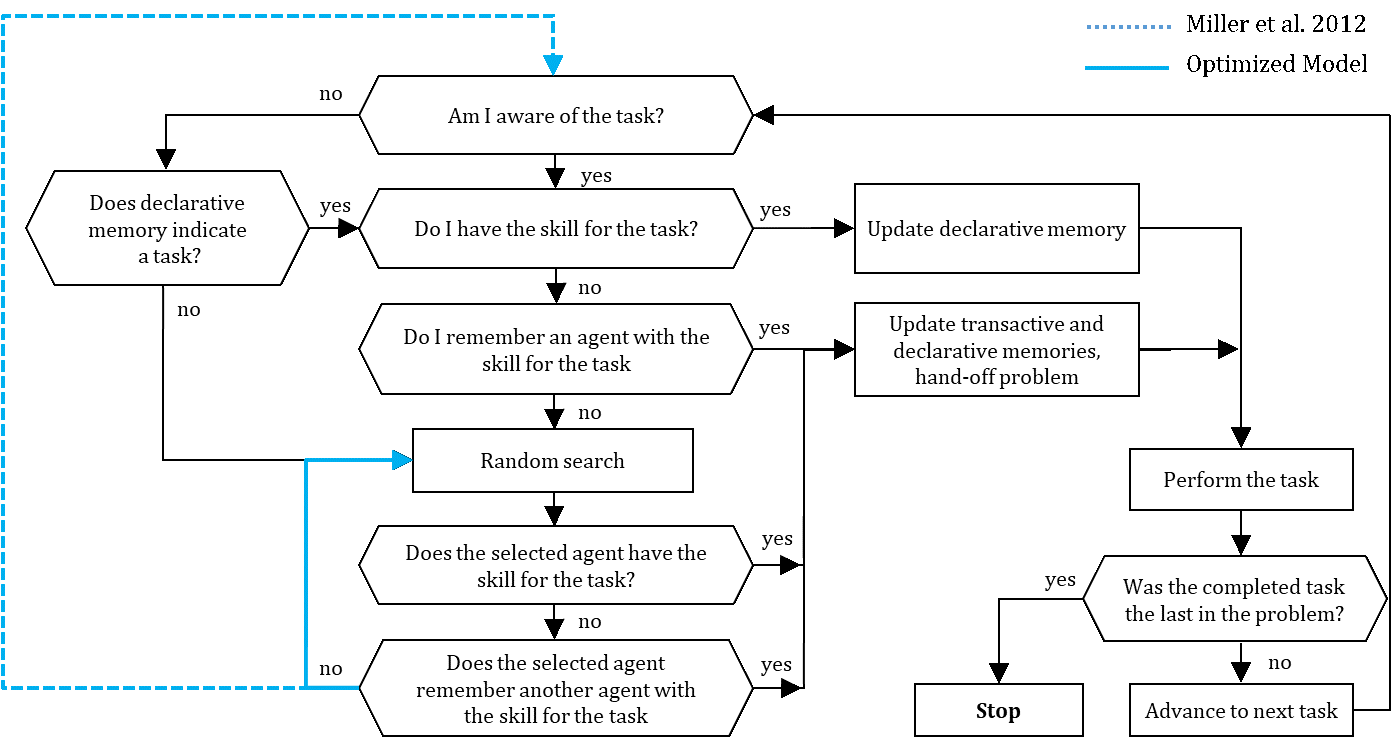
Agents self-organize the problem-solving process (see Figure 1) for given task sequences of the generated problems, except for the first task of each problem, which is always assigned to an agent that is aware of the task and has the required skill. An agent in charge of performing a task in a problem is also responsible for passing the next task in the sequence to another agent. Thus, the agent in charge might remember or must search for another agent that seems capable of handling the next task (Miller et al. 2012). As long as the performed task is not last in the problem sequence, each agent is responsible for advancing the solution by assigning an agent to the next task. Once a problem is solved, a new problem is generated, initiating a new problem-solving process (Miller et al. 2012).
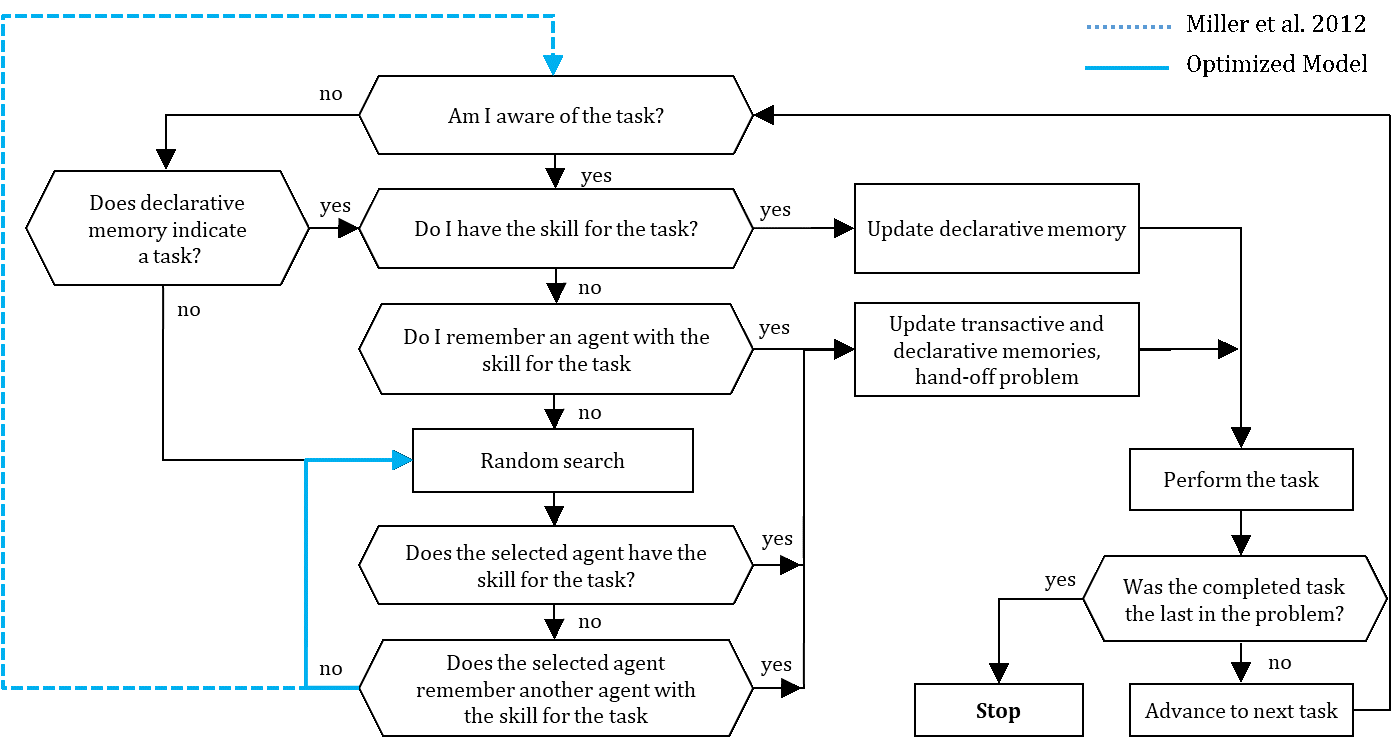
Organizational performance is measured by cycle time, calculated for each problem-solving process. Until a problem is solved, cycle time increases incrementally when agents (\(n\)) perform either necessary (\(n_t\)) or unnecessary (\(u_t\)) tasks and due to search costs (\(s_t\)) caused by unsuccessful random search attempts by agents. An organization achieves minimum cycle time if it only performs necessary tasks and if no search costs occur (Miller et al. 2012). The minimum cycle time equals the number of tasks in a problem.[13]
| $$\it{Cycle\, time}=\sum_{t=1}^{n_t}+\sum_{t=1}^{u_t}+\sum_{t=1}^{s_t}$$ |
Clarification of the Conceptual Model and Critical Reflections on the Design
The ODD protocol enables standardized descriptions of agent-based models with the intent to increase the efficiency of communicating conceptual models and preventing ambiguous model descriptions (Grimm et al. 2006, 2010). In particular, the ODD protocol fosters the clear, comprehensive, and non-overlapping model specifications required to replicate a model.
The ODD protocol can be used to transfer the unstructured, possibly scattered descriptions of a model into a standardized, accessible format for efficient subsequent consultation. A replicating modeler should avoid re-implementing a model from the original code to prevent bias (Wilensky & Rand 2007). Using the explicit intermediate result of the ODD protocol avoids this problem.
Experimental clarification of ambiguous model assumptions
We discovered an unclear assumption from the model description in Miller et al. (2012) when transferring their information into the structure of the ODD protocol. We clarified this ambiguity experimentally, without consulting the original code, to identify the underlying assumptions used in the original paper. The abstract model description also allows for model improvements without violating its original assumptions.
Specifically, Miller et al. (2012, p. 1542) state that the first task of a new problem is assigned at random to an agent that is skilled for this task. Hence, one can conclude that this statement is valid for each problem, although the modeled organization faces recurring problems by default. Another passage on changing problems makes this statement ambiguous, however:
To simulate a one-time exogenous change in the organization’s operating environment, we introduced a permanent change in the problem to be solved. For the 51st problem, the k (=10) tasks were randomly reordered, and the organization faced this new problem repeatedly for the remaining duration of a simulation run (Miller et al. 2012, p. 1548).
This passage suggests that new problems are characterized by reordered task sequences. Hence, one can also conclude that recurring problems are not new problems. This opens two different model assumptions:
- The first task of each problem is assigned to an agent who is skilled in that task.
- Only the first task of a changed problem with reordered task sequence is assigned to an agent who is skilled in that task.
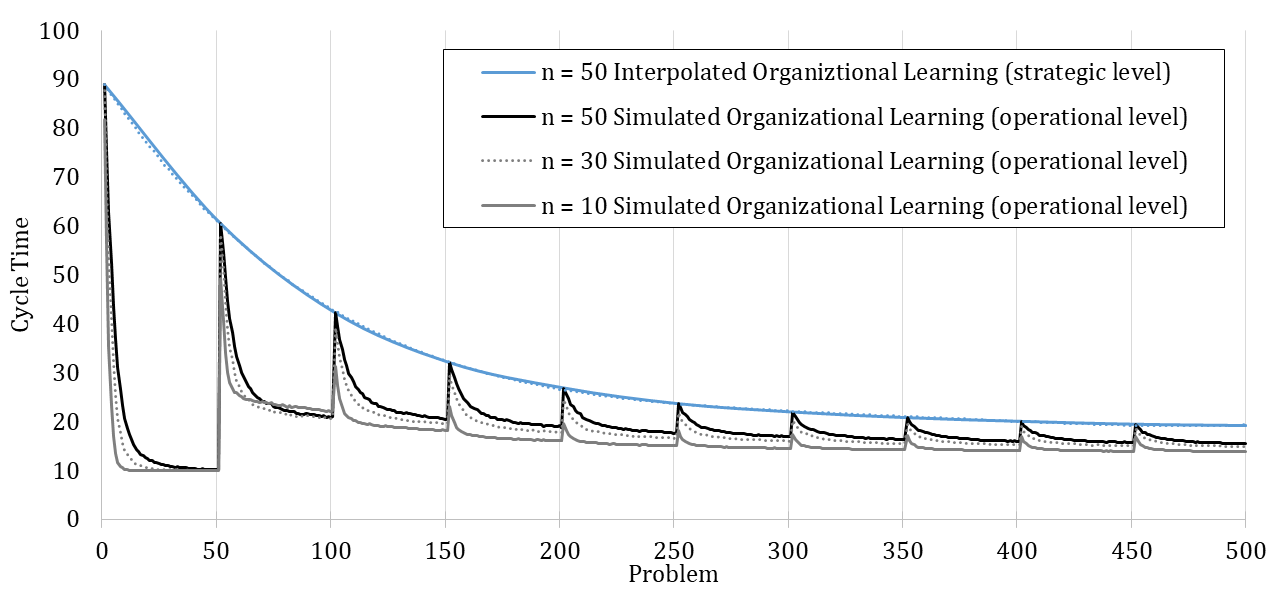
Figure 2 shows the simulation results of the re-implemented model, presuming either (A) or (B). Complementarily, we depict the results of the original model. We use the default parameter setting wherein the update probability of agents’ transactive memory (pt) is varied. The results indicate that the original model used assumption (A), as the resulting pattern better matches the original model.
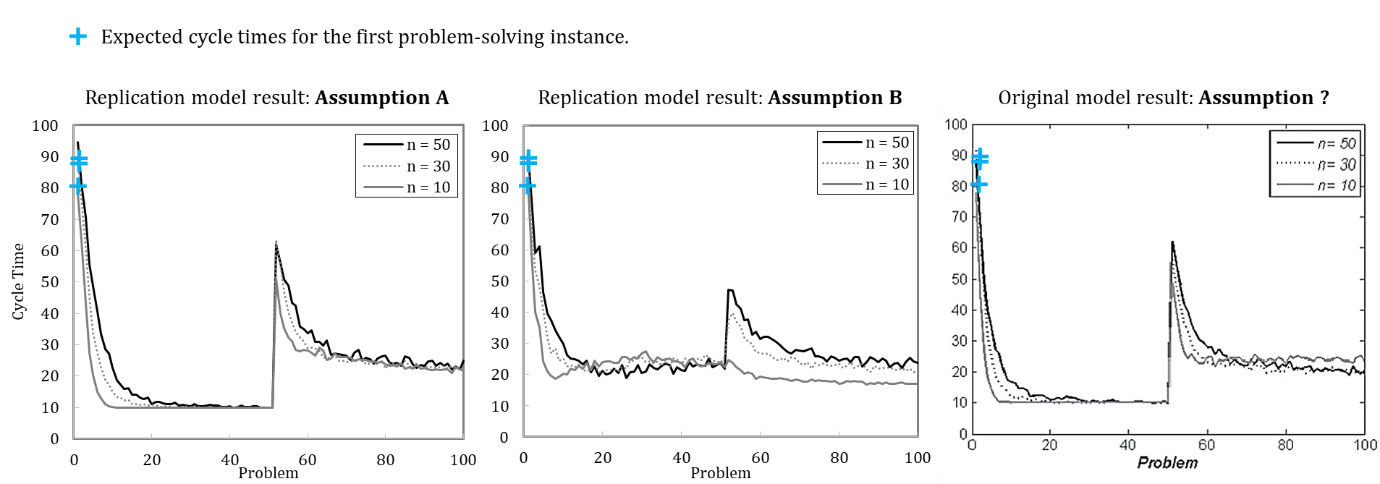
While a model description in the ODD format cannot protect against all ambiguities, it does make models’ conceptual foundations more explicit. The overall value of the standardized, ODD model description has been comprehensively discussed elsewhere (Grimm et al. 2006); here, we particularly emphasize its value for replication. Our precisely formulated submodel descriptions form a solid basis for writing corresponding functions in the NetLogo code. The model description in the ODD format explicitly expresses the formerly ambiguous assumption (see Appendix A, ODD Protocol, Submodels, problem generation, and task assignment). The final ODD description comprehensively specifies the model in an acknowledged format, which both helps other scholars to understand more precisely the model of Miller et al. (2012) and provides a solid ground for further extensions.
Critical reflections on the conceptual design
Transferring information from the conceptual model into the ODD structure enhanced our understanding of the model, and subsequent pretests revealed two opportunities for improvement.
Figure 1 highlights the first improvement. This modification does not break any model assumptions. In the modified flow chart, an agent searches randomly for agents until one accepts the problem. In the original model, a failed random search attempt results in repetitive scrutiny of the task and consultation of memory. This does not change the agent’s cognitive state, again resulting in a random search.
Second, we argue that random search can be more sophisticated. The original random search is designed as an urn model with replacement. The active agent randomly approaches other agents that might be able to perform the requested task or that can help the searching agent by making a referral to another skilled agent. After an unsuccessful search, the agent again searches randomly among all agents. Hence, the searching agent might approach the same agent again, implying that the searching agent would not remember which agents were approached unsuccessfully before. This assumption is counterintuitive and empirically unlikely. On the one hand, agents in general can remember other agents and their skills. On the other hand, agents do not remember meeting an approached agent during a search attempt. An alternative model design could be tested in which agents are also able to learn from an unsuccessful random search attempt. An alternative urn model without replacement would reduce the search costs and cycle time of a problem-solving process.
Overall, using the ODD protocol helped to define the conceptual model and revealed where the original model description allowed two contradictory assumptions. Furthermore, the ODD structure helped to identify opportunities for model improvements without violating the initial assumptions and highlighted alternative model designs that extend the original model.
Using DOE Principles to Evaluate the Replicated Model
Since the simulation model has stochastic elements, the results reported risk being unrepresentative, which could threaten the reliability of conclusions drawn from the simulation experiments. DOE principles, therefore, demand specification of the required number of runs based on the coefficient of variation for the performed experiments, [14] which allows consideration of stochastically induced variation and thereby enhances the credibility of results.
Our design incorporates low (L), medium (M), and high (H) factor levels, as highlighted in Table 3. These three design points reflect the applied settings to estimate the number of simulation runs needed to produce sufficiently robust results given model properties and stochasticity.
| Design Points | Factors | Representation | ||||
| \(n\) | \(a\) | \(p_t\) | \(p_d\) | \(w_d\) | ||
| L | 10 | 1 | 0.25 | 0.25 | 1 | Low factor levels |
| M | 30 | 5 | 0.5 | 0.5 | 25 | Medium factor levels |
| H | 50 | 10 | 0.75 | 0.75 | 50 | High factor levels |
Table 4 shows the error variance matrix with mean values and coefficients of variation for design point M (for the full error variance matrix, see Appendix C). We measured cycle time at five selected steps during the simulation runs, namely when the problems (P) 1, 25, 51, 75, and 100 are solved, to account for the dynamic characteristic of the dependent variable.[15] The coefficient of variation (\(c_v\)) is calculated as the standard deviation (\(\sigma\)) divided by the arithmetic mean (\(\mu\)) of a specific number of runs (Lorscheid et al. 2012). The cycle times in Table 4 result from different number of simulation runs ranging between 10 and 10,000. The coefficients of variation stabilize with increasing number of runs at about 5,000 runs; the mean values and coefficients of variation change only slightly from 5,000 to 10,000 runs. We therefore conclude that 5,000 runs are sufficient to produce robust results. [16]
With significant error variance detected for 100 simulation runs, results averaged over 100 runs or fewer should be carefully interpreted. Regarding the cycle time for the 25th problem, the coefficient of variation is 0.14 for 100 runs and 0.20 for 5,000 runs, which is a considerable difference. Visual comparison of experimental results based on 100 averaged runs is thus imprecise and error-prone compared to a comparison based on 5,000 simulation runs.
| Design points and dependent variable | Number of runs | |||||||
| 10 | 50 | 100 | 500 | 1000 | 5000 | 10000 | ||
| Cycle time (P1) | \(\mu\) | 95.80 | 89.44 | 88.19 | 90.15 | 88.61 | 87.98 | 87.86 |
| \(c_v\) | 0.24 | 0.29 | 0.32 | 0.30 | 0.31 | 0.31 | 0.31 | |
| Cycle time (P25) | \(\mu\) | 10.00 | 10.40 | 10.26 | 10.30 | 10.39 | 10.29 | 10.27 |
| \(c_v\) | 0.00 | 0.19 | 0.14 | 0.19 | 0.22 | 0.20 | 0.20 | |
| Cycle time (P51) | \(\mu\) | 59.50 | 59.04 | 57.36 | 58.82 | 59.00 | 58.43 | 58.32 |
| \(c_v\) | 0.31 | 0.28 | 0.31 | 0.32 | 0.33 | 0.32 | 0.32 | |
| Cycle time (P75) | \(\mu\) | 30.30 | 30.32 | 28.98 | 28.00 | 28.42 | 28.63 | 28.49 |
| \(c_v\) | 0.22 | 0.34 | 0.35 | 0.36 | 0.39 | 0.38 | 0.38 | |
| Cycle time (P100) | \(\mu\) | 19.20 | 22.08 | 22.77 | 23.03 | 23.14 | 22.97 | 22.95 |
| \(c_v\) | 0.25 | 0.46 | 0.43 | 0.42 | 0.41 | 0.41 | 0.41 | |
A high number of simulation runs also confirm the expected values for cycle time as determined analytically (see Appendix C), which offers further evidence that the conceptual model is implemented correctly. The analytically calculated cycle time for the first problem-solving instance (P1) of the medium-sized organization (n = 30) is 88.00, and the simulated average cycle time over 10,000 runs is close to this at 87.86. Such an approximate “numerical identity” is also found for a small organization (n = 10), with expected and simulated cycle times of 82.00 and 81.62, respectively, and for a large organization (n = 50), with anticipated and simulated cycle times of 89.20 and 89.52, respectively (see Appendix C).
To illustrate the value of defining the number of runs based on the coefficient of variation, we offer the following example. Miller et al. (2012) model in their final experiment an external change to and simultaneous downsizing of an organization; downsizing is thus modeled as a response to external change. The organization faces a changed problem once the 50th recurrent problem is solved. At the same time, the organization is downsized from (\(n\) = 50) to (\(n\) = 30) and from (\(n\) = 50) to (\(n\) = 10) agents.
Figure 3 shows the considerable increase in cycle time after simultaneous problem change and downsizing. In terms of cycle time, the organization that continuously operates with 50 agents peaks at 63, whereas the downsized organization of 30 members peaks at 73, and the downsized organization with ten members peaks at 83. Hence, downsizing initially interferes with organizational performance (see also Miller et al. 2012). The organization lost experienced members and their crucial knowledge for coordinating activities.
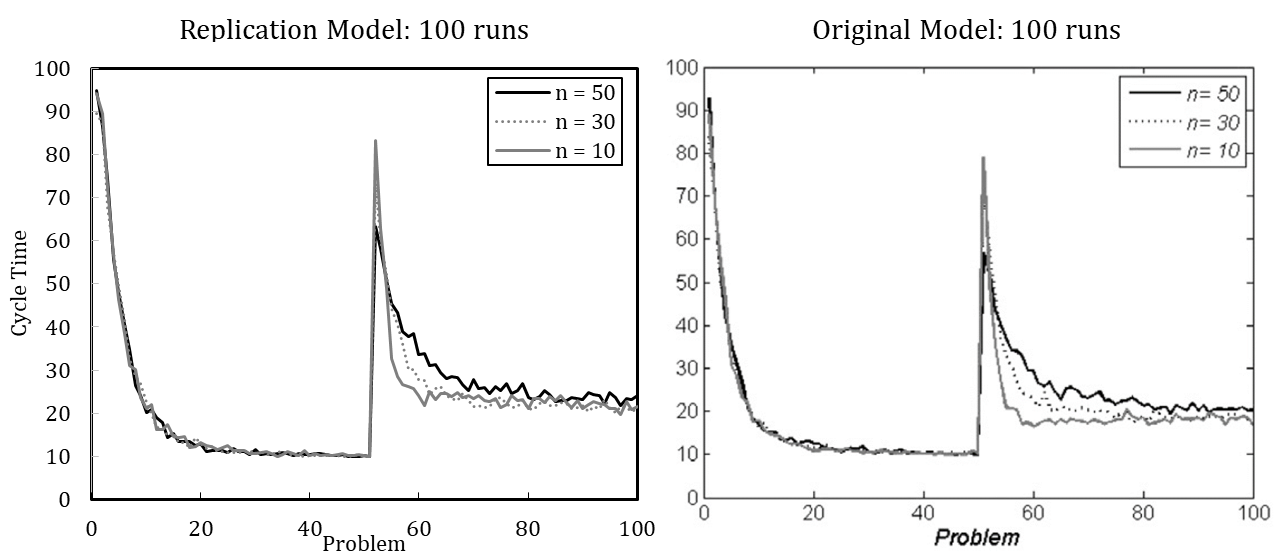
Although the averaged results of 100 simulation runs suggest that downsized organizations potentially learn more quickly in the new situation, no reliable statement can be made about which organization performs better after the change. [17] An increased number of runs enables more detailed interpretation (see Figure 4). The heavily downsized organization with only ten remaining members shows the highest performance after the change. At first, the heavily downsized organization performs worst, but learns much faster to handle the new situation. Still, none of the organizations regain optimal performance. This suggests that smaller organizations are more agile in creating a new knowledge network among agents.
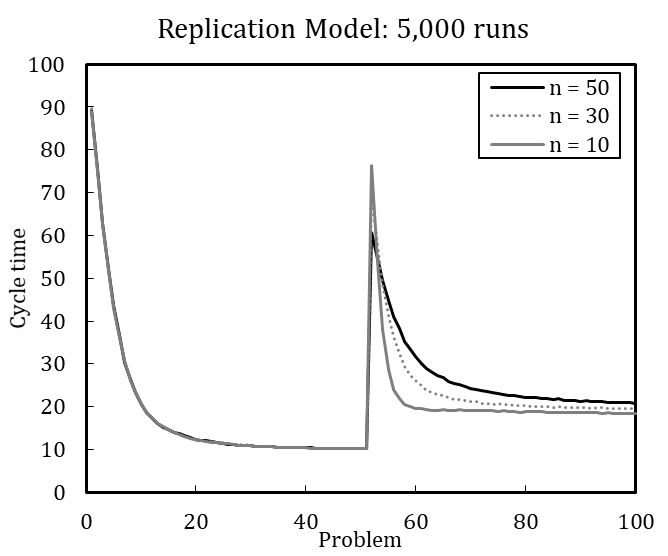
In line with this example, we have replicated each experiment of Miller et al. (2012) with 100 runs and with 5,000 runs (see Appendix B). The results, while qualitatively identical, nevertheless slightly differ quantitatively, which is likely driven by stochasticity. Based on the qualitative equivalence of the results, especially regarding the patterns in behavior after problem changes and downsizing, we conclude that the original model and our replication have identical assumptions.[18]
The simulation results show high variance derived from model stochasticity (for a detailed analysis, see Appendix C). We defined the coefficient of variation to improve our understanding of the model’s behavior and assess the precision of both our results and those as published by Miller et al. (2012). Calculation of effect sizes and interaction effects (see Appendix C) further deepened our understanding of the model’s behavior, offering still further evidence that both models behave identical.
Overall, applying DOE principles enabled us to analyze the model’s behavior systematically. For evaluating the replicated model, we found it crucial to determine the number of runs and understand stochastically induced variance. The replicated model produces quantitatively similar and qualitatively identical results. According to the classification of Axelrod (1997), the results are “relationally equivalent” and hint overall at “distributional equivalence” once error variance is taken into account. Hence, we conclude the model is replicated successfully.
Developing Theory with the Replicated Model
The following offers an example of how modest model extensions and in-depth analyses of simulation results can help consolidate insights and advance the understanding of vaguely specified concepts to develop theory. In a commonly used definition by Davis et al. (2007), theory comprises four elements:
Constructs, propositions that link those constructs together, logical arguments that explain the underlying theoretical rationale for the propositions, and assumptions that define the scope or boundary conditions of the theory. Consistent with these views, we define theory as consisting of constructs linked together by propositions that have an underlying, coherent logic and related assumptions.
Miller et al. (2012) address the theory of routines by Feldman & Pentland (2003), which states a reciprocal relationship between the performative and ostensive aspects of routines. The interaction between these two aspects, however, is only vaguely understood, with only partial empirical grounding (Biesenthal et al. 2019). Formal modeling provides the means to investigate underlying mechanisms by operationalizing theoretical constructs. In this respect, Miller et al. (2012) operationalize the dynamic interdependence of actions and memory distributed across an organization. In their computational representation, routines’ ostensive aspect is constructed via three types of memory residing in individuals distributed across the organization. As individuals draw on their memory to solve incoming problem sequences, the performative aspect of routines is made observable.
Davis et al. (2007) suggested a roadmap for developing theory using simulations, including the vital step of experimentation given the traditional strengths of a simulation: testing in a safe environment, low costs to explore experimental settings, and high experimental precision. New theoretical insights may be thereby generated by unpacking or varying the value of constructs, modifying assumptions, or adding new features to the computational representation.
We proceed from our successful replication to this crucial step of experimentation, developing theory in the following three ways: extension, in-depth analysis, and theoretical connection. First, we extend the model by exploring a merger in addition to the downsizing analyzed in the original study. By adding another scenario of external change, we extend the scope or boundary conditions and therefore further generalize the theory. Second, we analyze the model more deeply to show how an initial problem leads to a traceable path dependency in routine formation, gaining nuance on how memory functions affect the formation of routines. We thus unpack the theoretical constructs analytically rather than representationally. Third and finally, we elucidate connections to dynamic capabilities, taking our new insights back to the literature to look for intertwined processes not previously considered. In brief, we uncover the path dependency of routines (Vergne & Durand 2010), look for related theory, identify the concept of dynamic capabilities, and extend the experiment to investigate this concept in more detail.
The model simulates organizational routines, which Feldman & Pentland (2003, p. 2) define as “repetitive, recognizable patterns of interdependent action, involving multiple actors.” Feldman & Pentland (2003) conceptualized routines as adhering to recursively connected performative and ostensive aspects, [19] which helps explain the mechanisms of stability and change. [20] The ostensive aspect embodies the abstract, stable idea of a routine, while the performative aspect embodies the patterns of action individuals perform at specific times and places (Feldman & Pentland 2003).
Hodgson (2008) suggested defining routines as capabilities because of their inherent potential. The capabilities they generate are innate to organizations’ ambidextrous capabilities to balance the exploitation of existent competencies with the exploration of new opportunities (Carayannis et al. 2017). On the one hand, organizational performance is contingent on exploration so that the organization can remain competitive in the face of changing demands. On the other hand, organizational performance is contingent on the capability to exploit resources and knowledge. The latter type of performance can be measured in terms of efficiency, that is, a re- duction in cycle time by drawing on past experience (Lubatkin et al. 2006). Ambidexterity is usually related to fundamental measures of success such as firm survival, resistance to crises, and corporate reputation (Raisch et al. 2009).
Organizations’ ability to operate in a specific environmental setting is determined by the suitability of their routine portfolios (Aggarwal et al. 2017; Nelson & Winter 1982). Routines facilitate efficiency, stability, robustness, and resilience (Feldman & Rafaeli 2002); innovation (Carayannis et al. 2017); and variation, flexibility, and adaptability (Farjoun 2010). An underlying assumption is that organizations achieve optimal performance by finding appropriate responses to changes in the environment. Hence, organizations aim to align external problems with internal problem-solving procedures so they may respond adequately to their environment and maintain equilibrium between internal (organizational) and external (environmental) aspects (Roh et al. 2017).
Generalizing theory: Routine disruptions when organizations merge
Besides downsizing—which Miller et al. (2012) studied, as mentioned above—mergers are another frequent activity by which organizations respond to external changes (Andrade et al. 2001; Bena & Li 2014). Because mergers require the integration of new personnel, human resource issues are critical, but the literature on mergers and acquisitions often neglects this aspect (Sarala et al. 2016). Therefore, to complement the experimental results of Miller et al. (2012) concerning downsizing, we investigate a merger scenario to generalize the understanding of routine disruptions.
Organizations comprise personnel with different experiences, which, as indicated by previous results, are crucial to form routines. Thus, we expect that integrating new staff, whether experienced or inexperienced, affects post-merger routine performance. We model untrained employees as agents with empty declarative memory (a) and model experienced employees as agents with randomly replenished declarative memories (b), thereby assuming that agents have some operational knowledge. [21] Figure 5 depicts organizational performance under different post-merger processes of routine formation. The following analysis models the merger activity as an organization’s response to an external shock, as reflected by a change in problem.

Case 1 represents an organization that integrates new personnel in stable environmental conditions. This integration initially disrupts the original routines whether the new personnel members are inexperienced (a) or experienced (b), which negatively affects organizational performance in a similar pattern as downsizing, albeit less intensively (see Appendix B). The integration of inexperienced personnel (Case 1a) allows organizations to form new routines with optimal performance, suggesting that the new staff adopt the lived routines. In contrast, the integration of experienced personnel (Case 1b) results in lower organizational performance, even in the long run; the new staff does not completely unlearn obsolete sequences of task accomplishment. [22]
Case 2 represents an organization that integrates new personnel in response to an external shock, as reflected by a problem change. The change and simultaneous integration of new personnel force the organization to learn new routines. The learning curves of merged organizations are quite similar to those of downsized organizations (see Appendix B). Organizations with new, inexperienced personnel (Case 2a) perform worse, suggesting that the new staff is not well integrated; organizational behavior is predominantly determined by core personnel (n = 10). On the other hand, organizations integrating experienced personnel (Case 2b) can form routines that result in optimal performance.
We can now generalize that mergers and downsized organizations show similar patterns in organizational performance (see Appendix B); both involve disrupted routines. Comparison between Cases 1 and 2 shows the conditions under which merging organizations can develop efficient routines. The finding that mergers can initially decay adherence to routine agrees with empirical results (see, e.g. Anand et al. 2012). Moreover, the literature on successful mergers highlights the importance of forming new, high-order routines that can resist blocking effects from existing routines; successful mergers can then, afterward, realize radical innovations (Heimeriks et al. 2012; Lin et al. 2017). In other words, the success of a merger depends on individuals’ experience, as this affects whether lived routines can be maintained and whether new efficient routines can be formed.
In conclusion, organizations that downsize or merge as a response to an external shock stimulate the formation of new routines. We found that both downsizing and merging initially reinforce the disruption of established routines. Loss of organizational knowledge initially reduces performance in downsized organizations, but such organizations quickly form new, efficient routines. In a complementary finding, Brauer & Laamanen (2014) found that the pressure of downsizing on the remaining individuals forces them to engage in path-breaking cognitive efforts that can lead to better results than the repair of routines by drawing on experience. In a further generalization of the ideas Miller et al. (2012) presented, we conclude that the routines of organizations are similarly affected when organizations downsize or merge in response to an external shock.
Deeper analysis: Routine persistence in organizations facing volatility
If routines are a recurrent pattern of actions, the question remains which patterns can emerge. An appropriate organizational routine matches the task sequence of the problem at hand. Some less efficient organizations, however, struggle to coordinate their activities with the problem. In particular, inappropriate behavior by agents might create unnecessary activity.
To explore the link between the behavior of individuals and emerging routines, we performed an experiment in which an organization again begins by facing 50 recurrent problems. The organization thereby has the chance to form a routine. Thereafter, it faces 50 different problems, each characterized by a new, randomly shuffled task sequence[23]. Hence, the modeled organization must adapt to multiple, distinct problems. At the end of the simulation, in the 100th problem-solving instance, we measure the frequency of emerging patterns of actions to investigate whether the organization has unlearned the routine, initially developed over the first 50 problems, that has since become obsolete.
Table 5 shows the frequencies of subsequently performed tasks by the organization. The matrix contains the relative frequency of performed actions as measured on the 100th problem-solving instance of a simulation, averaged over 5,000 runs. The actions that the organization performs to solve the generated problems comprise necessary (73%) and unnecessary actions (23%). Most combinations of subsequent, accomplished tasks occur similarly often, with a probability of around 1%. However, a few interdependent actions have a likelihood of emerging around 2%. These correspond to the subsequent, ordered tasks of the initial problem.
| Subsequent performed task | |||||||||||
| Performed task | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 0 | 0.00 | 2.97 | 1.13 | 0.79 | 0.63 | 0.66 | 0.57 | 0.59 | 0.61 | 0.54 | |
| 1 | 0.69 | 0.00 | 2.85 | 1.40 | 1.07 | 1.05 | 1.00 | 0.95 | 0.91 | 0.91 | |
| 2 | 0.97 | 0.72 | 0.00 | 2.55 | 1.36 | 1.07 | 1.09 | 1.04 | 1.04 | 0.99 | |
| 3 | 0.97 | 0.95 | 0.79 | 0.00 | 2.48 | 1.29 | 1.11 | 1.06 | 0.99 | 0.96 | |
| 4 | 1.07 | 0.99 | 0.91 | 0.78 | 0.00 | 2.26 | 1.27 | 1.14 | 1.03 | 0.98 | |
| 5 | 0.98 | 1.01 | 1.03 | 0.92 | 0.79 | 0.00 | 2.06 | 1.23 | 1.03 | 0.96 | |
| 6 | 0.91 | 1.03 | 0.99 | 1.00 | 0.86 | 0.78 | 0.00 | 2.07 | 1.18 | 0.97 | |
| 7 | 0.97 | 0.98 | 0.94 | 1.00 | 0.99 | 0.90 | 0.74 | 0.00 | 2.07 | 1.20 | |
| 8 | 0.96 | 1.05 | 1.00 | 1.01 | 1.04 | 0.91 | 0.91 | 0.71 | 0.00 | 2.00 | |
| 9 | 1.00 | 1.14 | 1.17 | 1.15 | 1.14 | 1.14 | 1.09 | 1.03 | 0.75 | 0.00 | |
The initially learned routine (to solve the recurrent problems numbered 1 to 50) persists. Although the organization copes more recently with diverse situations (random problems 51 to 100), the prior, learned behavior of the organization remains traceable. This persistence of organizational behavior matches the detected behavior of individuals (see Appendix E). Individuals and the organization maintain obsolete knowledge, implying that an organization’s past pattern of action partially persists. Recurrent patterns of interdependent actions reduce organizational performance if these actions do not match the situation at hand. Developed routines can be detrimental when an organization faces change.
The development of organizational capabilities in terms of routines is path dependent (Aggarwal et al. 2017). The results of a similarly designed experiment offer further support. When the organization exclusively copes with different problems, the original action pattern remains traceable (see Appendix F). Therefore, one might consider this development of organizational capabilities to be path dependent. This is in line with some scholars position, portraying routines as organizational dispositions or even genes.[25] However, conceptualizing routines as dispositions is untenable, because other factors, such as individuals’ high task awareness, can prevent the persistence of routines (see Appendix C).
Refining simple theory: Dynamic capabilities
If processes of knowledge integration could provide micro-foundations for dynamic capabilities, the model of Miller et al. (2012) resembles knowledge-integration routines, conceptualizing an individual’s memory as three different types or functions. The distinct properties of an agent’s memory function correspond to distributed, specialized knowledge in a firm. To solve collective problems, agents coordinate their actions based on their memory functions. The ability to learn from previous actions leads to the development of routines with recurring properties for problem-solving, with the formation and performance of these routines affected by distinct properties of individual’s memory.
We found that an initial problem leads to traceable path dependency in the routine-formation process, which prevents an organization from again reaching initially achieved cycle times after an external shock and thereby constituting a natural limitation on dynamic capabilities. This newly gained insight motivates a closer investigation of the effects of such path dependencies on dynamic capabilities, using our replicated model.
The model enables interpretations from an operational and strategic perspective. On an operational level, a change in problem decreases organizational performance because established working procedures become obsolete and forming new routines requires search costs. This consideration is short term, however. On a strategic level, organizations that face environmental changes have the opportunity to learn; in the long run, the experience thus gained might improve their capability to handle such changes.
In Figure 6 an organization learns sequentially over ten different problems with 50 problem instances each, highlighting the organization’s performance on both levels. The individuals in the organization search for new paths to adapt their activities to new situations induced by the problem changes. The organization thereby develops operational capabilities to reduce the cycle time between problem changes and gains a dynamic capability over the long run to manage external changes.
The organization’s dynamic capability emerges from the cognitive properties of individuals.[26] The development of such dynamic capabilities has, according to the model design, two prerequisites. First, individuals can revise their declarative memories so that they can change their learned problem-solving sequence. Second, the internal staffing structures of the organization are non-rigid. The more individuals are forced to search for new paths to solve problems, the more likely they are to search for and randomly meet other individuals. This yields an experienced organization comprising members who know each other very well. The organization exploits this knowledge when it faces a change. Modeled here is an ambidextrous organization that can both exploit acquired knowledge and explore new paths.
Organizations that recurrently encounter external changes develop dynamic capabilities that enable them to handle changes in an experienced manner, which enhances their operational performance during crisis-like events. Overall, the simulation offers evidence that organizations can form both dynamic and operational capabilities based on routines formed through individual’s memory functions. In the long run, organizations that regularly form new routines develop dynamic capabilities. Given this result, we hypothesize that even an organization operating in a highly volatile environment can form routines.
Therefore, we model a volatile environment using continuous changes in problem. Figure 7 shows the averaged results over 5,000 simulation runs for three different organizations operating in volatile environments. We set the model parameters to the defaults except for the memory update probabilities of individuals. The organization without memory (\(p_t =\) 0 and \(p_d =\) 0) is unable to learn and solves problems exclusively through random search, which results in consistently poor performance over time. The simulated cycle time is approximately 89.20, which tracks the analytically determined cycle time (see Appendix D). The organization with transactive and declarative memory (\(p_t =\) 0.5 and \(p_d =\) 0.5) can learn and performs better over the long run. The organization with transactive memory but without declarative memory (\(p_t =\) 0.5 and \(p_d =\) 0.0) shows, in the long run, the best operational performance in the volatile environment.

The results suggest that organizations can learn and form routines, even in volatile environments. Routines may be flexibly enacted based on organizational experience through mechanisms that can be explained by incorporating the previous findings.
Transactive memory allows agents to learn about the skills of their colleagues, implementing a network for who knows what. Continuously changing problems force agents to coordinate to accomplish tasks, which teaches agents about the skills of multiple colleagues. Agents in charge of but not skilled at or aware of a task draw on their personally developed networks.[27] Most agents, by gaining experience over time, develop such networks, which are interrelated. They allow the organization to retrieve distributed knowledge and flexibly coordinate whichever activities are appropriate to the current situation. [28]
Agents’ declarative memory negatively affects organizational performance in the midst of volatility, standing in contrast to its positive effect in stable environments. Besides their personal networks, agents’ actions also result from their learned problem-solving sequence, which becomes inappropriate when tasks change. The resulting behavior is then detrimental to organizational performance and perturbs the formation of efficient routines.
In summary, individuals’ learning capabilities enable organizations to form efficient (meta)routines, independent of environmental conditions. The performance of organizations in terms of learning varies with the type of memory combined with the type of environment. The particular effect of transactive memory was highlighted in a follow-up study by Miller et al. (2014), which applied a similar model design. Investigating organizations operating in volatile environments, we found that individuals’ transactive memory enables organizations to develop dynamic capabilities, while their declarative memory can weaken that effect.
Overall, our results show that individual and organizational learning are antecedents of the development of both routines and dynamic capabilities in organizations, as Argote (2011) had postulated. Individuals in an organization learn problem-solving sequences and apply their knowledge, which is a prerequisite for the formation of routines. This positively affects organizational performance as long as the organization operates in a stable environment. However, a learned problem-solving sequence is detrimental to organizational performance when conditions change, although this detrimental effect is not necessarily linear, because interactions among individuals can compensate for some problem-inappropriate behavior.
Routines are related to the concepts of cognitive efficiency and the complexity of problem-solving processes (Feldman & Pentland 2003), but existing literature has not examined whether environmental shocks and volatility counter the cognitive efficiency generated by organizational routines (Billinger et al. 2014). Using the replicated model, we demonstrated that organizations can form routines while operating in volatile environments. When problems change frequently or continuously, such (meta)routines are not detectable merely based on observable patterns of action.
Conclusion
This paper used a replication of a simulation model, namely that of Miller et al. (2012), to develop theory, and demonstrated the benefit of using standards, such as ODD and DOE, in the replication process. Our replicated model produces quantitatively similar and qualitatively identical results that are “relationally equivalent” and hint overall at “distributional equivalence,” following the classification of Axelrod (1997).
Replications of simulation models must rely on published conceptual model descriptions, which are often not straightforward (Will & Hegselmann 2008), even for a relatively simple model, as was the case here. The use of the ODD protocol fosters a full model description through its sophisticated, standardized structure. It is an explicit intermediate result that provides a steppingstone in the replication process (Thiele & Grimm 2015). Transferring the original model description published by Miller et al. (2012) into the ODD format helped to identify formally ambiguous assumptions that we subsequently clarified during pretests with the re-implemented model.
The application of DOE principles was also helpful in several respects. The original model results were unavailable as raw data, presented mainly graphically, averaged over 100 simulation runs, and subject to stochastic influences. Using the DOE principles suggested by Lorscheid et al. (2012), we quantified statistical errors to determine 5,000 simulation runs as an appropriate number enabling reliable visual comparison of graphically depicted outputs. The results of the replicated model generated on this basis match those highlighted by Miller et al. (2012). Hence, we primarily exclude errors due to stochasticity in the replicated results. Moreover, the application of the DOE principles yielded insight into model behavior and validated simulation results against the conceptual model. Analyses of the original code further increased the credibility of the replication.
Our successfully replicated and then verified model offered a solid foundation for further extensions and experiments to develop and refine theory. First, we generalized previous theoretical insights by investigating a merger scenario in addition to the downsizing scenario examined in the original paper, finding a similar qualitative pattern for both. Either disrupts an organization’s established routines, initially reducing performance due to lost organizational knowledge, but organizations can quickly form new, efficient routines. Second, we illustrate how replicated simulation models may be used to refine theory, such as analyzing in-depth the relationship between memory functions and the performance of routines. In this respect we show that initially learned routines persist, locating their path dependence in the memory functions of individuals. Progressing from this finding, new experiments with multiple problem changes allow us to clarify and formally specify a potential mechanism (Smaldino et al. 2015) underlying the still actively debated theoretical concept of dynamic capabilities. Here, given the longitudinal and processual character of the concept, as well as the fact that empirical data are challenging to obtain, simulations offer comparative methodological advantages (Davis et al. 2007). Table 6 gives a summary of how we develop theory with the replicated model.
| Theory | Miller et al. | Replication | Result | Theory development |
| Organizational routines | ||||
| Organizational downsizing scenarios | Organizational merger scenarios | Downsized and merged organizations show similar disrupted performance patterns (=new boundary condition) | Generalization of theory through its extended scope | |
| Routine formation and performance measured by cycle time | More in-depth analysis of developed action patterns and path dependencies | Organizational inertia results from the persistence of few initial learned problem-solving patterns (=path dependency) | Theory refinement via specification of the mechanism of how memory functions affect routine formation | |
| Dynamic capabilities | ||||
| Operational (short-term) performance of organizations facing one crisis event (one problem change) | Strategic (long-term) performance of organizations facing a volatile environment (multiple problem changes) | Distinct understanding of the formation of operational and strategic capabilities of organizations | Conceptualization of routines in context of dynamic capabilities. Theory refinement by deconstructing knowledge routines | |
Some limitations exist, as well. We document the benefits of using the ODD protocol and DOE principles with respect to a replication endeavor. Also, as discussed above, we used quite a large number of runs to obtain stable results. The model’s abstract design enables general interpretations, but its assumptions have not been validated empirically. Moreover, we investigate dynamic capabilities with respect to knowledge integration, but the foundations of the concept of dynamic capabilities are not restricted to this respect. Nevertheless, the agent-based model depicts a potential fundamental mechanism for routine formation and what affects their performance.
The model suggests promising directions to explore in future research on organizational routines. First, the performance of routines that organizations enact to handle volatility could be empirically investigated. Second, regarding model design, future research could test additional submodels. For example, agents’ search could be modeled as an urn model without replacement, which would reduce organizations’ search costs and cycle times. Third, regarding the use of the ODD protocol and DOE principles in model replications, we suggest further testing of these standards in future replication studies to more broadly establish their benefits.
Acknowledgements
We would like to thank the anonymous reviewers for their valuable comments and suggestions that helped us to enhance the quality of the article. This publication was supported by funding program “Open Access Publishing” of Hamburg University of Technology (TUHH).Notes
- One could argue that simulation models that are not independently replicated have only marginal scientific value due to their prototype character.
- Procedural memory reflects agents’ “know how,” declarative memory reflects their knowledge of “what to do,” and transactive memory reflects “who knows what” (for a comprehensive description of the three memory concepts of routines see Miller et al. (2012, p. 1539). Agents draw information from their memory to perform routines.
- Based on Google Scholar citations through June 2019. Another model — Pentland et al. (2012) — has 338 citations, but it is not agent-based (Kahl & Meyer 2016). For a more recent agent-based model of routines, see Gao et al. (2018).
- The studied conceptual model is, in principle, generic, shifting the focus to verification of the fit between the conceptual and implemented models. In explaining their assumptions, the authors refer briefly to the example of a medical service unit (see Miller et al. 2012, p. 1542), but their conceptual model can represent diverse organizational settings because of its design at a high level of abstraction.
- One incentive to replicate agent-based models was the Volterra Replication Prize, but the prize has not been awarded since 2009 (http://cress.soc.surrey.ac.uk/essa2009/volterraPrize.php).
- However, we want to recognize the trend within the ABM community to make models and accompanying data fully available online (Hauke et al. 2017; Janssen 2017). Therefore, setting an example for good scientific practice in comparison to other disciplines, where transparent data sharing is often still lacking.
- To our surprise, the authorsdo not mention agent-based modeling among the listed simulation approaches, which is perhaps why they fail to highlight implications of the strength of the Keep It Descriptive, Stupid (KIDS) approach — handling social complexity in connection with theory development (Edmonds & Moss 1984) — in favor of the Keep It Simple, Stupid (KISS) approach.
- We acknowledge that such a view on theory is not uncontroversial. However, the discussion of what makes a theory unsettles philosophy of science until today. We see their concept of simple theory as a useful substantiation of the to be developed building blocks of a theory: “Constructs, propositions that link those constructs together, logical arguments that explain the underlying theoretical rationale for the propositions, and assumptions that define the scope or boundary conditions of the theory” (Davis et al. 2007). Explicitly addressing these building blocks supports the process of theory development as an evolutionary process (Weick 1989; Whetten 1989). As such, it might be understood as a theory under construction.
- For an assessment of the concept of dynamic capabilities as a theory, see Denrell & Powell (2016).
- We also screened the MATLAB code of the original model for anomalies and misspecifications.
- The replicated model code can be found at (https://www.comses.net/codebase-release/ua01596-e2cd-4979- 96c4-b1ad2ce9ac23/) (file name: Dynamics of Organizational Routines: A Model Replication).
- If skills are not approximately distributed uniformly among agents, this can lead to different results, as highlighted in the original study.
- Cycle time does not increase when an agent scrutinizes or hands off a task to another agent who accepts the problem. This simplifying assumption implies that scrutinizing tasks and handoffs requires no effort.
- Miller et al. (2012) provided no information regarding how they chose the number of simulation runs or regarding the coefficient of variation.
- Recall that the problem changes after the organization solves the fihieth problem.
- We acknowledge that this number of runs is rather high. In this study, we aimed to obtain particularly stable results to enable visual comparison with the original graphs. See, in this respect, discussions regarding Figures 4 and Figure 5. More recent approaches to determining the appropriate number of runs adopt a power analysis framework (Secchi & Seri 2017), which supports an argument for fewer simulation runs. As a matter of fact, Secchi & Seri (2017) concluded that the original simulation experiments with the model are overpowered, while the majority of investigated papers in their review lacked sufficient model runs and are therefore underpowered. Having too many runs poses the risk, besides the added computational costs, that economically insignificant results become statistically significant. For this reason, we argue that effect sizes should be considered to distinguish between economic and statistical significance. For a discussion of the problems of over- and underpowered simulation experiments, including issues with Error Type II, see Secchi & Seri (2017).
- Another advantage of having a replicated model is that we can now calculate the respective effect sizes. We calculated Cohen’s d for the relevant effects; they fall in the range assumed by Secchi & Seri (2017).
- Moreover, after we completed the replication we examined the code provided by Miller et al. (2012). The basic processes correspond to the flow chart depicted in Figure 1, and key model elements were implemented the same, conceptually, as in our replicated model.
- Miller et al. (2012) denominate these aspects as performative and ostensive routines.
- The term “organization” also refers to organizations within organizations; that is, departments are suborganizations within firms.
- Knowledge can represent experience gained in another organization or acquired in training. For example, an employee might learn to follow a new procedure that does not correspond to the previously lived routine.
- In Germany, in line with this result, Tesla avoids recruiting experienced personnel from the automotive industry (according to a personal conversation with one of the authors).
- The random shuffling of tasks in a sequence of \(k\) tasks allows the generation of \(k!\) distinct problems, or with 10 tasks, as in the experiment here, 10! = 3,628,800. An identical sequence is unlikely to reoccur.
- The occurrence probability that tasks are immediately repeated is very low. Agents with a misleading notion of what to do can get stuck in loops in which the problem is passed between agents. Such loops are broken in the model. Therefore, we exclude entries on the matrix diagonal for calculating the occurrence probabilities.
- For example, a new company might develop a particular behavior in its start-up phase. This behavior be- comes the company’s disposition (firm culture). The company might act according to this disposition even years later.
- The strategic learning curve can be approximated by a polynomial function of the fourth degree: \( y = 4e^{-09}x^4 - 5e^{-06}x^3 + 0.0028x^2 – 0.6979x + 89.655; R^2 = 0.99 \).
- An extended explanation according to the model design follows: An agent that is aware of a task performs it. Otherwise, the agent searches for help from another agent. The approached agent is likely to have different task awareness. Thus, both agents taken together are, with a higher probability, aware of what to do. The approached agent also knows other agents and is thus often able to refer the task to an agent that can perform it. A distant (random) search is then unnecessary.
- The formation of such routines depends on organizational size. In volatile environments, small organizations are more agile and form routines faster compared to larger organizations.
- If skills are not approximately distributed uniformly among agents, this can lead to different results.
- In pretests with the replication model, different submodels were tested to clarify ambiguous assumptions.
- Cycle time does not increase when an agent scrutinizes or hands off a task to another agent who accepts the problem. This simplifying assumption implies that scrutinizing tasks and handoffs require no effort.
- One might regard downsizing as an endogenous change.
- Recall that the problem changes after the organization solves the fiftieth problem.
- An averaged calculation of cycle time over several problem-solving instances would deteriorate the informative value of the effect sizes..
- The 35 factorial design and 5,000 repetitions of each simulation run yields 35 × 5,000 = 1,215,000 simulation runs in total.
- No main effect or interaction effects are observable for declarative memory capacity, because the capacity is not varied below the value of 1. Agents are always capable of solving a subsequent task. Moreover, in the initial routine-formation phase, declarative memory contains only correct entries. Therefore, it does not matter how often a correct, subsequent task is stored.
- Moreover, an appropriate number of simulation runs is incorporated to obtain representative results.
- Moreover, transactive memory always indicates correctly who knows what.
- The occurrence probability that tasks are immediately repeated is very low. Agents with a misleading notion of what to do can get stuck in loops in which the problem is passed between agents. Such loops are broken in the model. Therefore, we exclude entries on the matrix diagonal for calculating the occurrence probabilities.
Appendix
A: ODD protocol
Purpose
The model aims to show how the cognitive properties of individuals and their distinct types of memory affect the formation and performance of organizational routines in environments characterized by stability, crisis (see Miller et al. 2012) and volatility.
Entities, state variables, and scales
Entities in the model are agents, representing human individuals. The collective of agents forms an organization. Table 7 reports the model parameters. The global variables are the numbers of agents and tasks. By default, the organization comprises (\(n = 50\)) agents. The organization faces problems from its environment. A problem involves a sequence of (\(k = 10\)) different tasks (Miller et al. 2012). The organization must perform the tasks in a given order to solve a problem; the order of tasks defines the abstract problem in terms of its complete solution process. Once the organization performs each task in the required sequence, the problem is solved (Miller et al. 2012). The organization solves several problems over time, which can either recur or change in terms of the required task sequence. The time an organization requires to solve a problem is defined as cycle time (Miller et al. 2012), which represents organizational performance.
| Variable | Description | Value (Default) |
| n | Number of agents in the organization | 10, 30, 50 |
| k | Number of different tasks in a problem | 10 |
| a | Task awareness of an agent | 1, 5, 10 |
| pt | Probability that an agent updates its transactive memory | 0.25, 0.5, 0.75, 1.00 |
| pd | Probability that an agent updates its declarative memory | 0.25, 0.5, 0.75, 1.00 |
| wd | Declarative memory capacity of an agent | 1, 25, 50 |
Table 7 further defines the individual variables used to set agent behavior. Agents are heterogeneous in terms of skill, but the skills themselves are not varied and are thus not reflected by a variable. Each agent has a particular skill stored in its procedural memory that enables the agent to perform a specific task ( Miller et al. 2012). On the one hand, the number of agents equals at least the number of different tasks in a problem, thus ensuring that an organization can always solve a problem, if the organization can organize the task accomplishment in the defined sequential order. On the other hand, the number of agents can exceed the number of tasks (\(n > k\)) ( Miller et al. 2012). In such cases, the \(k\) different skills are assumed to be uniformly distributed among the agents.[29]
Any agent is aware of \(a\) randomly assigned tasks (Miller et al. 2012). Each agent is aware of a limited number of tasks of a problem (1≤ a ≤ k). An agent’s awareness set contains at least the task for which they are skilled, thus assuming that agents who can perform a specific task are also capable of recognizing this task. Agents are otherwise blind to unfamiliar tasks (Miller et al. 2012).
Declarative memory enables agents to memorize the subsequently assigned task once they have performed their task. Agents have limited declarative memory capacity (wd =1) and memorize a task with a probability set by the variable (\(p_d\) =0.5) (Miller et al. 2012). Further, agents can memorize the skills of other agents in their transactive memory. The number of agents and their skills which each agent can memorize is limited by the number of agents in the organization. The probability that an agent adds an entry to their transactive memory is defined by the parameter (\(p_t\) = 0.5) (Miller et al. 2012).
The agents are distributed across the organization. Scale and distance are not modeled explicitly, but time is crucial in two ways. On an operational dimension, the problem-solving process requires the accomplishment of tasks, as measured by the cycle time. An organization that consecutively solves problems over time might form routines.
Process overview and scheduling
The organization faces consecutive occurring problems. The generated problems trigger organizational activities. Except for the first task of each problem, the agents self-organize the problem-solving processes given the task sequences of the generated problems. The first task in each task sequence is assigned to an agent that is skilled to perform the task. An agent in charge of performing a task in a problem is also responsible for passing the next task in the sequence to another agent. Thus, the agent in charge might remember or must search for another agent that seems capable of handling the next task (Miller et al. 2012). Then, the agent in charge hands the problem over to the identified agent, who then becomes in charge of the problem (Miller et al. 2012).
Figure 8 depicts the schedule that an agent follows when in charge of a problem. An agent first scrutinizes the task. If the agent is aware of and skilled for the task, the agent updates its declarative memory and perform the necessary task. The agent then advances to the next task if the problem has not yet been solved (Miller et al. 2012).
An agent that lacks the skill to perform the task at hand starts a local search process. An agent that is aware of the task but not skilled consults its transactive memory. If the transactive memory reveals another agent skilled to perform the required task, the searching agent tries to hand the task off to this agent. An agent that is unaware of a task consults their declarative memory, which might reveal a task that is usually due. If declarative memory indicates a task (what usually should be done), the agent further consults the transactive memory (of who has the appropriate skill) to hand the task over to a skilled agent. If this local search is unsuccessful or if an agent’s memory is undeveloped, the agent proceeds with a distance search process to handoff the problem (Miller et al. 2012).
Distance search involves a random search for a skilled agent to hand over the problem. If the searching agent finds a skilled agent, the agent updates the respective types of memory and hands off the problem. An approached agent without the skill required for the task of the searching agent might nevertheless be able to make a referral to another agent. In this case, the searching agent hands off the task to the referred agent and updates the transactive and declarative memory (Miller et al. 2012). An unsuccessful search attempt results in a new random search.
As long as the performed task is not last in the problem, an agent advances to the next task of the problem. Once a problem is solved, a new problem is generated and a new problem-solving process is initiated (Miller et al. 2012).
Design concepts
Basic principle
The model design is abstract. Conceptually, it proceeds from the idea that organizational routines form as a result of individuals’ cognitive properties and activities. The model is designed from the perspective of distributed cognition: the individuals are distributed and have distinct properties. The model assumes that individuals self-organize the problem-solving process and adapt their behavior to recurrent or different problems. Individuals can learn, which affects the coordination of activities and organizational performance.
Emergence
Organizational routines emerge from individuals’ initially independent skill sets and capacities (Winter 2013). The micro-foundations on the individual level are thus well-reasoned and explicitly modeled. Organizational macro-behavior is not explicitly modeled. The organizational behavior that emerges from the properties of the individuals is analyzed. The presumed emergent phenomenon is that the modeled organization develops routines over time.
Adaption
The individuals in the organization adapt their activities to recurrent and changing problems. Recurrent problems reflect stable environmental conditions. In this case, the organization adapts to the problem by forming a routine. A crisis event is modeled as a one-time change in problem, which forces the organization to adapt to the new situation and learn a new routine. A volatile environment is modeled as a continuously changing problem, in which the organization has to cope with varying conditions. The organization might even instantiate routines to operate efficiently in such a volatile environment. In terms of the flexible use of action patterns and their adaption to certain situations, routine dynamic can be traced back to individuals (Howard-Grenville 2005). Since individuals perform activities contingent on their situations, routines can be applied flexibly in a volatile environment (Adler et al. 1999; Bogner & Barr 2000).
Objectives
The organizations’ objective is to organize the problem-solving process as efficiently as possible in terms of cycle time. Agents’ primary objective is to perform tasks and to organize the problem-solving process. Overall, agents follow this objective to ensure the completion of all task sequences for each occurring problem.
Learning
Learning is an important design concept. On the individual level, agents have three types of memory: procedural, transactive, and declarative. In procedural memory, agents store their skill (Miller et al. 2012). According to the model design, each agent owns one skill; agents are assumed to have learned the skill in prior training. Agents do not learn new skills; agents are assumed to be specialists in their roles. Agents learn through their transactive and declarative memory. Transactive memory allows the agents to store who knows what in the organization. Declarative memory enables the agents to learn what should usually be done given a problem’s task sequence. On the macro level, the organization can learn to handle problems in a routinized manner.
Prediction
Prediction by agents in the organization is only implicitly modeled. Agents that are not aware of a task at hand try to predict the task from the information in their declarative memory. Agents not skilled to perform the task at hand try to predict who else in the organization is skilled to perform that task. This prediction is based on their transactive memory.
Sensing
On the macro level, the organization senses problems. On the micro level, agents sense tasks. Their awareness models their sensing capabilities. Organizational sensing capabilities depend on the organization’s ability to include task-aware agents in the problem-solving process at the right time.
Interaction
Interaction between two agents is communication in which they can exchange information about a task, their skills, and the skills of other agents. Communication can also result in a problem being handed over between the agents. This interaction is not explicitly modeled, task handoffs may encompass communication or a virtual or physical exchange of work in progress.
Moreover, after task handover, the transmitting agent can observe the actions of the receiving agent. Some scholars of social cognition distinguish such social observations from interactions (see e.g. Tylén et al. 2012), but one might indeed consider this observation to be an indirect interaction.
Stochasticity
Organizations that regularly face problems from the environment might not be aware of the specifics of a particular problem. This is reflected by stochasticity. Moreover, an organizational member who searches for a colleague with a particular skill but has no clue whom to ask will ask randomly chosen colleagues. This random choice is also modeled as stochasticity.
Collectives
An organization is the resulting collection of individuals, the personnel at a company. Furthermore, within the organization, small collectives or dyads can form. Dyads form, for example, when an agent interacts with another agent to hand over a task or to exchange information about other colleagues.
Observations
The performance of an organization is observable as cycle time. The model allows the observation of cycle time under different conditions, since the problem and the parameters of the individuals can be varied.
Initialization
The model is initialized according to the variable settings. After agents of the organization are created, an initial problem is generated. The model is generic and requires no input.
Submodels [30]
Problem generation and task assignment
The problems comprise a set of \(k\) tasks [\(1. . . k\)]. Based on random distribution, the tasks are initially shuffled to reflect a specific problem that the organization must solve. In a stable scenario, each problem is generated with an identical task sequence. A crisis event is modeled as a permanent change in a problem: the task sequence is shuffled once. A volatile scenario is modeled as a continuous change in a problem: the task sequence is shuffled for each problem or following a defined frequency. In any case, the first task of a problem is always assigned to an agent that is aware of and skilled in performing the task.
Agents scrutinize tasks
An agent scrutinizes a task at hand to check if the task is represented in their awareness set.
Random search
An agent’s random search attempt is modeled as an urn sample with replacement. The searching agent draws another agent to approach at random. This search attempt is successful if the searching agent finds another agent to take the task. Otherwise, the agent searches again, repeating the search until an approached agent accepts the task.
Communication between searching and approached agents
Agents communicate to hand over tasks. This communication also affects which task is performed next and particularly depends on agents’ task awareness. Agents that are aware of a task at hand approach an agent to perform the required task. Agents who are unaware of a task but have a notion of what to do due to their declarative memory approach an agent to perform the requested task. The response of the approached agents depends on their task awareness and skill. Four responses are possible: [1a] the agent is aware of and skilled for the required task and performs it; [1b] the agent is aware of but unskilled for the required task and tries to make a referral to another agent with the skill to perform it; [2a] the agent is unaware of the required task but skilled for the requested task and performs this necessary or unnecessary task; [2b] the agent is unaware of and unskilled for the requested task and tries to make a referral to another agent with the skill for the requested task ( Miller et al. 2012).
Problem responsibility and task handover
An agent hands off a task if another agent is found to have the skill to perform the required or requested task. With the task handoff, the approached agent becomes responsible for the problem, while the agent handing over the task relinquishes responsibility for it. Thus, always one single agent in the organization is responsible for advancing the problem-solving process.
Declarative memory
Agents observe and can learn what is done next. An approaching agent that hands off a task to another agent has the chance to store the information of the task performed next in their declarative memory. An experienced agent who is unaware of a task can draw on declarative memory to obtain an idea of what usually should be done. In this case, the agent assumes that the next task is the one that occurs most frequently in the declarative memory. This assumption can be misleading, particularly if the problem has changed over time.
Transactive memory
An agent that hands off a task to another agent has a chance to learn about the skill of the successor. Agents store this information in their transactive memory, updated with the probability (\(0 \leq p_t \leq 1\)).
Necessary and unnecessary task accomplishments
Agents perform two types of tasks: necessary tasks, according to the given task sequence, and agents are homogenous, resulting from task requests by searching agents with a wrong notion of what to do based on the wrong interference from their declarative memory. The problem-solving process only advances with the accomplishment of necessary tasks.
Cycle time
Cycle time measures the length of time taken for organizations’ problem-solving processes and is calculated for each problem individually. Until a problem is solved, cycle time increases incrementally when agents (\(n\) perform either necessary (\(n_t\)) or unnecessary (\(u_t\)) tasks and due to search costs (\(s_t\) caused by unsuccessful random search attempts by agents. An organization achieves minimum cycle time if it only performs necessary tasks and if no search costs occur (Miller et al. 2012). The minimum cycle time equals the number of tasks in a problem.[31]
| $$\textit{Cycle time}=\sum_{t=1}^n n_t + \sum_{t=1}^n u_t + \sum_{t=1}^n s_t $$ |
B: Replicated experiments and reproduced results
The effect of individual transactive memory on the initial formation of a routine
In the first experiment, we investigate how individuals' transactive memory affects routine formation when an organization faces a recurrent problem. We test four different settings of memory update probability (\(p_t\)); other model parameters are held constant and to their defaults.
Figure 9 compares the results produced with the replicated model to those produced by the original model. Both show that the organization’s problem-solving efficiency is affected by individuals’ transactive memory. The cycle time decreases over time as the organization learns to efficiently handle the recurrent problem. The organization’s capability of forming efficient routines depends on agents’ cognitive properties. High capacity of agents to remember who knows what results in high organizational performance. That is, the gradient of the organizational learning curves depends on their individual properties. Over the long run, the organization approximates optimum performance (cycle time = 10) when operating on recurrent problems (see also Miller et al. 2012).
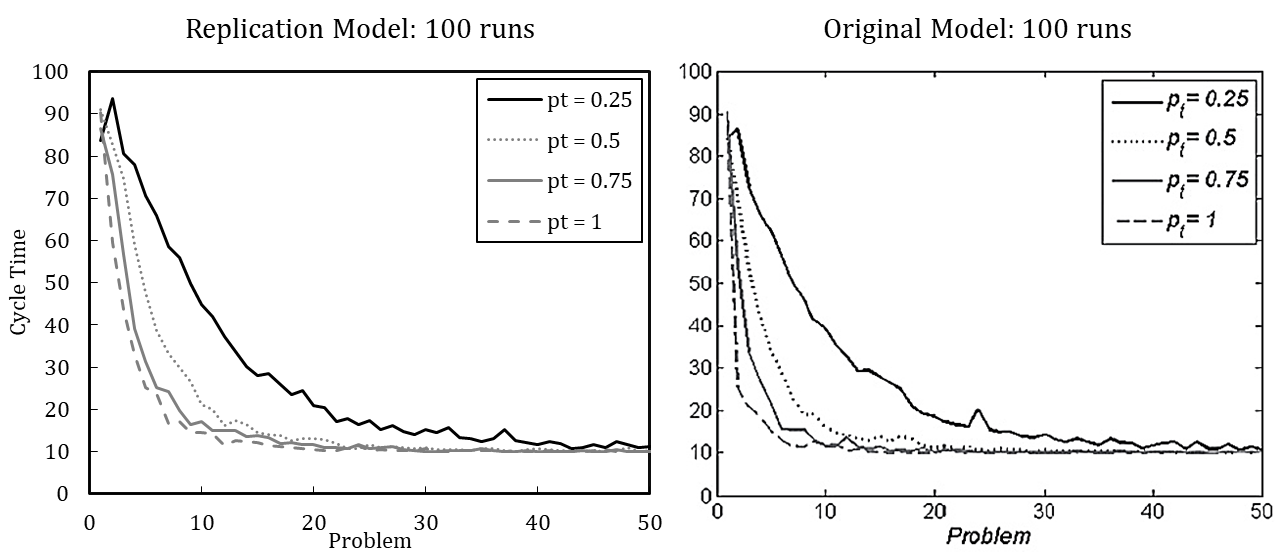
While the overall qualitative result is the same between the replicated the original simulation, quantitative divergences must be discussed. The replicated model shows, for a low value of (\(p_t\)) and in the first two problem- solving instances, an increase in the average cycle time from 84 to 94. In the original model, the cycle time does not exceed 90. Which result is correct? The divergence could be due to a mistaken model assumption or stochastic variance. Therefore, Figure 10 depicts the results averaged over 5,000 simulation runs.
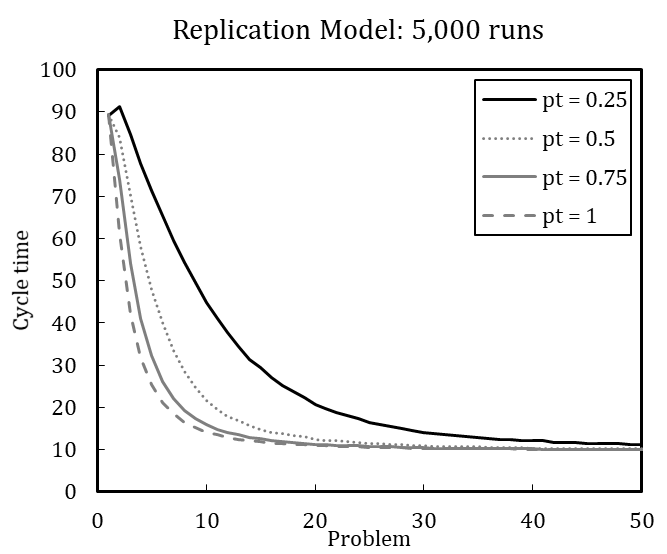
The graph shows smooth learning curves compared to results averaged over 100 runs. This indicates that the model has high stochastic variance that can be reduced by a higher number of runs. Although the three results are qualitatively similar, they are quantitatively different.
The effect of individual declarative memory on the initial formation of a routine
The second experiment is performed to investigate the effect of declarative memory on an organization's routine-formation process. Similar to the first experiment, the parameter values of (\(p_d\)) are varied, and the other parameters are held constant. The organization again faces a recurrent problem.
Figure 11 depicts the resulting cycle times for the repetitive problem-solving process of the modeled organization. The generated results of the replicated model again show learning curves decreasing to approximate the optimal cycle time, as expected. Different parameter settings of (\(p_d\)) appear to have a small effect, indicating that higher declarative memory capability among members slightly increases the organization's learning capability. Thus, individual learning enables the organization to reach higher routine performance in less time.
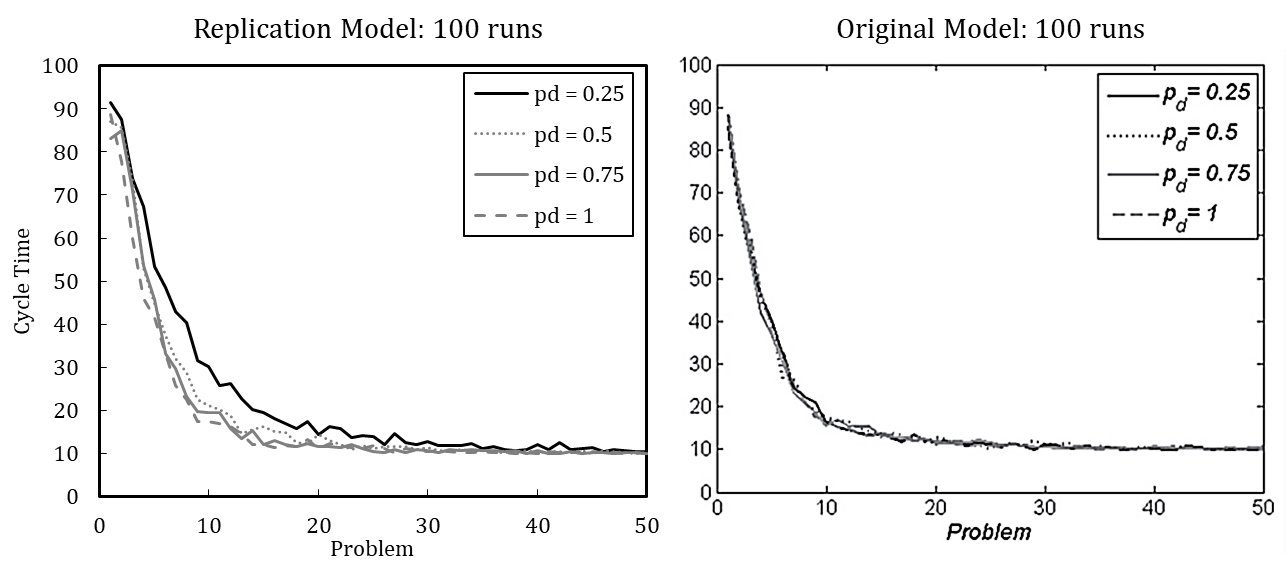
In the original, published results have no effect on routine formation and performance with a varying parameter (\(p_d\)) becomes visible. Nevertheless, Miller et al. (2012) explain they found an effect of declarative memory, but the euect is low, because agents can discern half of the tasks (\(a =\) 5). Furthermore, they mention a high update probability for declarative memory could substitute for low task awareness. Figure 12 depicts the averaged results over 5,000 simulation runs, which allows more precise determination of the influence of declarative memory.
While the effect of declarative memory is low, a higher update probability of declarative memory does make organizations quicker to form routines. Indeed, the divergences between the original and replicated results demand an investigation of experimental error (see Appendix C). However, Miller et al. (2012) stated that declarative memory affects routine formation in this setting due to the model design: “If the agent holding the problem is unaware of the next task, then it presumes that the next task is that occurring most frequently in its declarative memory associated with the task it just completed” (p. 1543).
Consequently, an agent’s declarative memory can substitute for lacking task awareness. Moreover, agents initially learn the correct sequence because the helping agents are aware of the task a searching agent is looking for and thus, correctly decide what should be done next:
If the agent completed the task for the first time, so that its declarative memory is blank, then the agent moves to step 2 in the search process and seeks help from a randomly chosen agent who happens to be aware of the next task in the problem ( Miller et al. 2012, p. 1555).
Hence, if organizations face recurrent problems, agents’ declarative memory can correctly substitute for lacking task awareness. This positively affects organizational performance, although the effect is weak, as the authors noted:
Over a wide range of positive values (0.25 \(\leq p_d \leq\) 1), the probability of remembering past task sequences has little effect on the cycle-time path. Because agents can discern half of the tasks (\(a =\) 5) and the task sequence is fixed across problems, agents quickly fill the gaps in their knowledge of the task sequence needed to solve problems. ( Miller et al. 2012, p. 1546).
In summary, the authors mention, and the replicated results show that declarative memory (\(p_d\)) has a slight effect on the initial formation of routines. The authors reason this effect logically, but do not provide experimental evidence. Our replication discovers small effects also experimentally, suspecting the divergence from the original model founded in the model stochasticity.
Routine disruption due to downsizing
The third experiment is performed to analyze what happens if the organization loses staff. In this experiment, the organization faces recurrent problems and then abruptly drops staff when the fiftieth problem is solved. Two scenarios are analyzed: a moderate staff reduction from 50 to 30 and a substantial reduction from 50 to 10 organizational members.
Figure 13 highlights the resulting learning curves of the organization. In both cases, the cycle time greatly in- creases once the organization downsizes. In the extensive downsizing scenario, the average cycle time peaks at 79; in the moderate scenario, it peaks at 47. This indicates that downsizing, particularly extensive downsizing, disrupts an initially formed routine. The loss of organizational knowledge explains this effect. However, once the downsized organization has solved approximately ten more problems, it regains optimal performance, implying that the organization formed a new routine. Moreover, the extensively downsized organization recovers slightly faster (see also Miller et al. 2012).
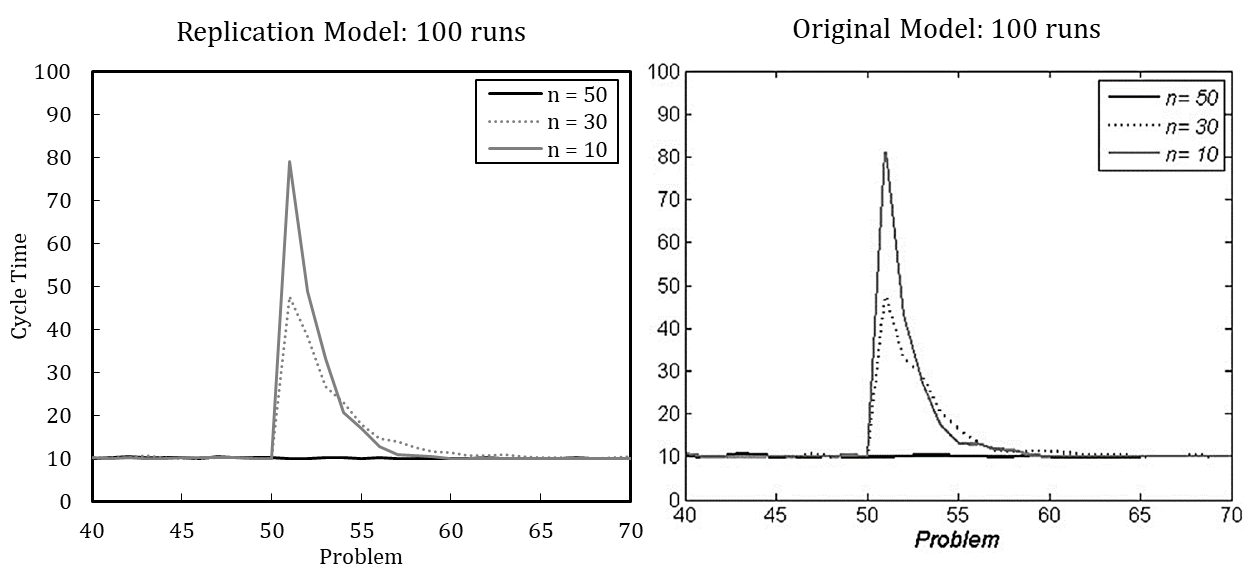
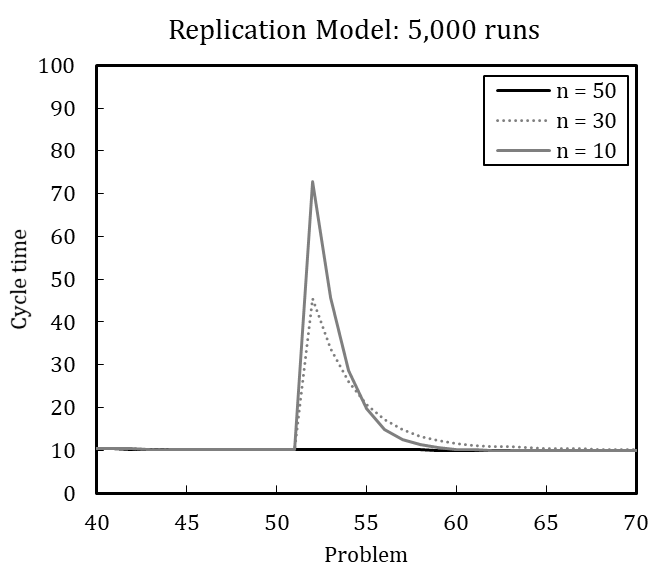
A comparison between the replicated and original results shows that they are quite similar. The moderately downsized organization recovers more slowly because learning in this organization is distributed over more redundant agents ( Miller et al. 2012). This supports the hypothesis that organizations might fail to adapt due to their inertia. [32] Moreover, the cognitive properties of the organization depend not only on the properties of its constituting elements. The number of redundant elements also matters and increases the effort required for coordination.
The averaged results over 5000 simulation runs (see Figure 14) offer evidence of the reliability of the results from both models, especially the conclusion about which size of organization recovers more quickly, since the differences are quite small.
Adaptation of routine to an external change contingent on organization size
Experiment 4 represents an external change, modeled as a permanent, one-time change in problem. This is considered an environmental change because organizations do not influence the given problem structure. Figure 15 illustrates the formation of routines when organizations with 10, 30, and 50 members face such a change after solving fifty problems. The problems one to fifty and the problems fifty-one to one hundred are identical (see also Miller et al. 2012).
Initially, organizations learn to handle the recurrent problem, as observed in the previous experiments. Small organizations learn faster than larger organizations. Once the problem changes, the organization’s initially formed routines fail to meet the new challenge. The disruption in routine results in an abrupt increase in cycle time. The organization’s acquired experience is obsolete. Beyond that, organizational knowledge hampers the formation of new efficient routines, as the organization does not achieve the optimal cycle time again. This indicates that organizations are unable to unlearn initially learned routines. On the micro-level, this might be explained by persistent and misleading entries within individuals’ declarative memory that impede the learning of new task sequences (see also Miller et al. 2012). Thus, organizations get stuck in less than optimal routines caused by residuals of prior routines.
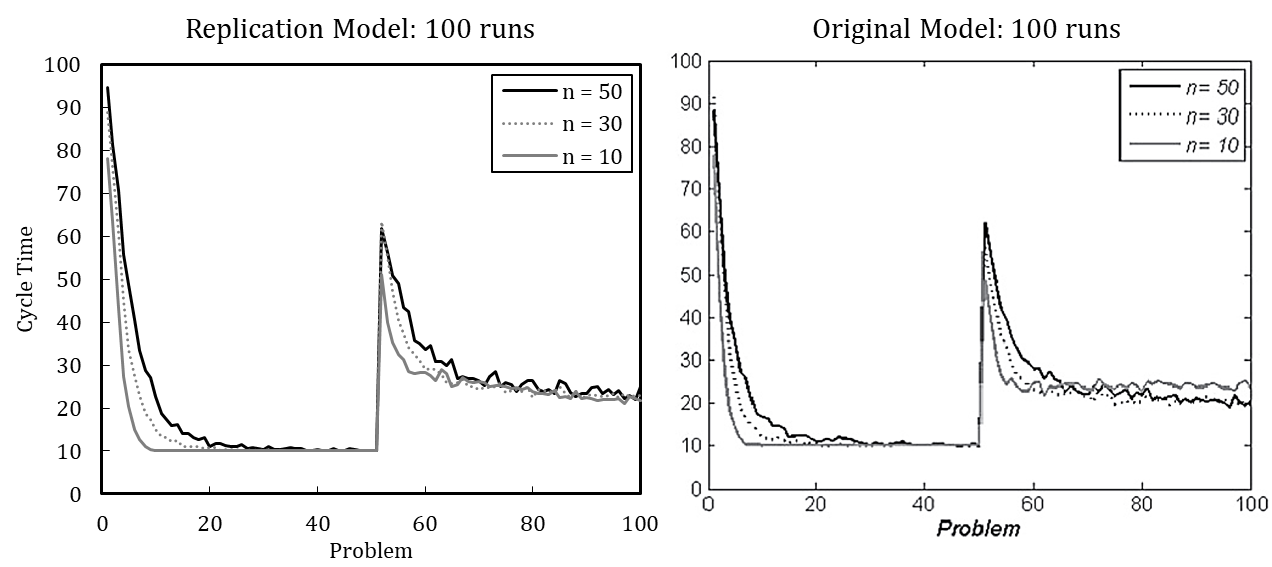
The averaged results over 100 simulation runs do not make it possible to predict which organization performs better over the long term. The averaged results over 5,000 runs suggest that bigger organizations develop better performing routines over the long run, although, smaller organizations recover faster (Figure 16).
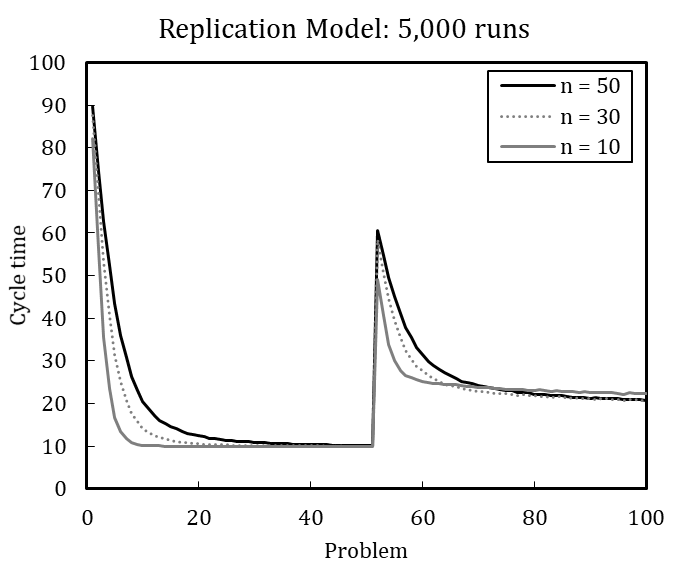
However, an explanation of long-term performance is given by neither (Miller et al. 2012) nor by a simple ex- amination of the model design and experiment. This demands investigation in this scenario and the agents’ declarative memory states that reflect their knowledge base.
Adaptation of routine to an external change contingent on declarative memory
In Experiment 5, similar to the previous experiment, organizations again face an external change, but agents’ declarative memory capacity (\(w_d\)) is analyzed. Figure 17 illustrates the learning curves of two organizations comprising agents with different declarative memory capacities (\(w_d =\) 1 and \(w_d =\) 50). Once the problem changes, the organizations’ formed routines collapse, as observed in the previous experiment. The organization comprising agents with a rather low declarative memory capacity shows a slightly higher performance in the long run (see also Miller et al. 2012). This indicates that highly experienced organizational members may re- strain adaptation. Organizational unlearning of obsolete activities might thus be hampered because outdated memory remains stored across the distributed system.
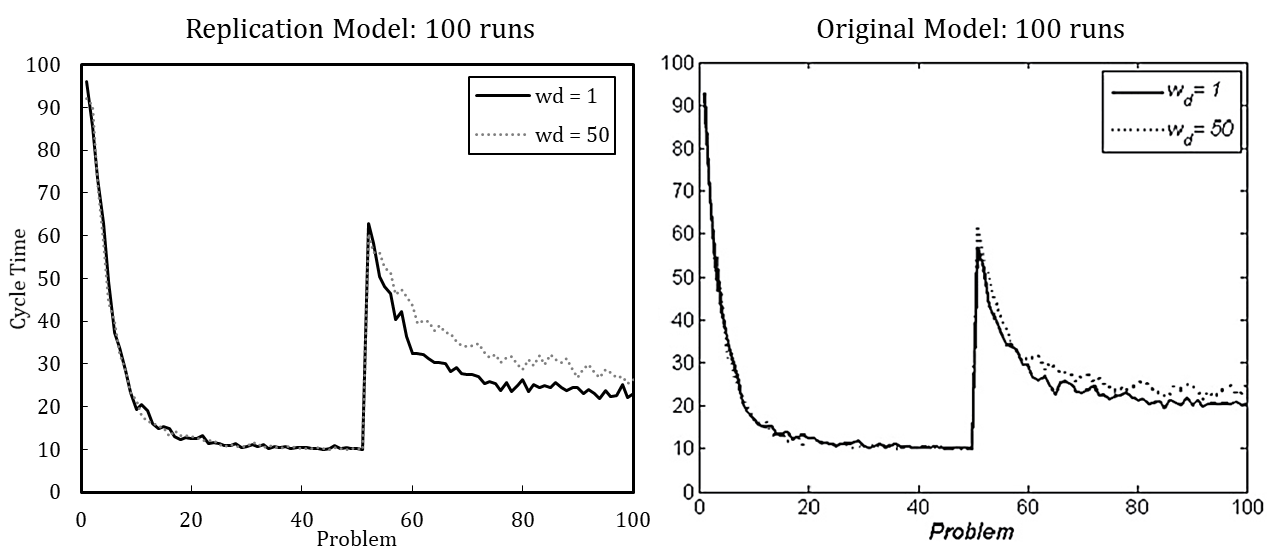
The results generated with both models and those averaged over more simulation runs are qualitatively com- parable (see also Figure 18). The replicated results indicate that declarative memory capacity does not affect initial routine formation. In the initial phase, agents exclusively memorized the correct subsequent task. Therefore, it does not matter if they store the right task only once or fifty times. This result gives further evidence that the replicated model is built on the same assumptions as the original.
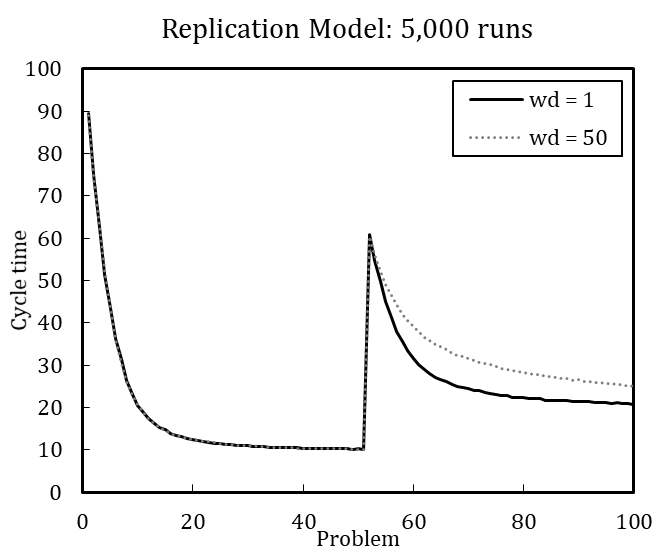
Given the external change, the precise effect size of the parameter (\(w_d\)) remains unclear. The analysis also shows that the complexity of the modeled behavior increases when the problem changes due to agents' learning capability.
Adaptation of routine to an external change contingent on task awareness
Experiment 6 is designed to test how agents' task awareness affects organizations' adaptive properties. This experiment is similar to experiments 4 and 5, but agents' task awareness is varied (\(a =\) 1, \(a =\) 5, and \(a =\) 10). Furthermore, the experiment addresses the substitution of task awareness with declarative memory. Figure 19 depicts the organizational learning curves.
The replicated model shows that agents’ task awareness has a marginal effect on the initial formation of routines. Agents with high task awareness enable their organizations to form routines more efficiently compared to organizations comprising agents with low task awareness. Once the problem changes, this effect intensifies. Indeed, organizations with agents that have limited task awareness cannot recover their previously achieved performance (see also Miller et al. 2012). The presence of obsolete declarative memory can again explain this observation; organizations must have members with high task awareness to unlearn old routines.
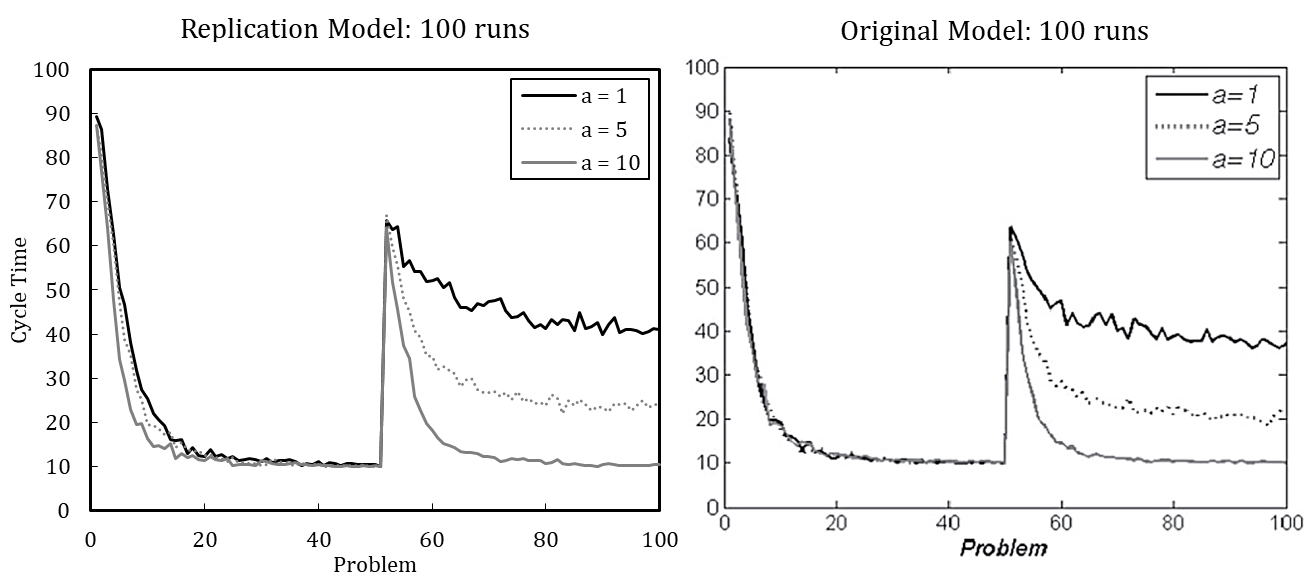
The results of both models are qualitatively similar, but the replicated model has slightly deviating curves in the initial routine-formation phase. These marginal difference becomes visible when averaged over 5,000 runs (Figure 20).
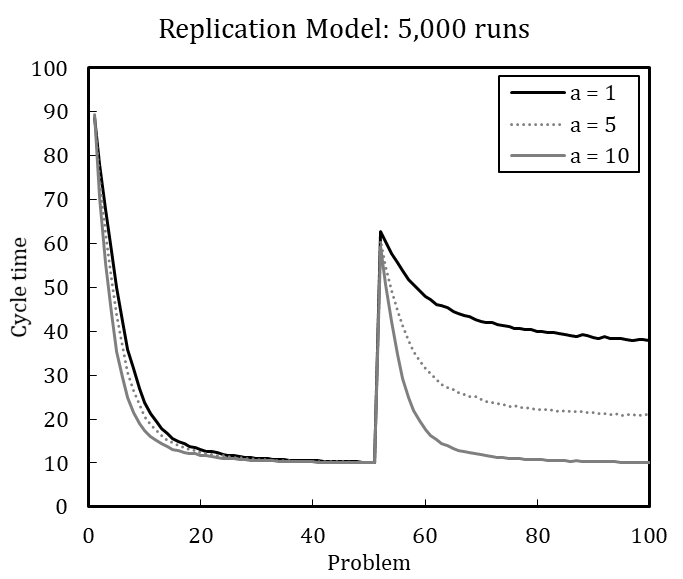
Routine adaption throughout an external change and simultaneous downsizing
(This experiment is discussed in Section 6 of the main text to exemplify how DOE principles enabled systematic analysis of model behavior and results. For readability and to provide a complete overview of all replicated experiments in this appendix, we present it again below.)
The final experiment models an external change to and simultaneous downsizing of an organization; downsizing is thus modeled as a response to external change. The organization faces a changed problem once the 50th recurrent problem is solved. At the same time, the organization is downsized from (\(n =\) 50) to (\(n =\) 30) and from (\(n =\) 50) to (\(n = \)10) agents. Figure 21 shows the considerable increase in modeled cycle time after simultaneous problem change and down- sizing. In terms of cycle time, the organization that continuously operates with 50 agents’ peaks at 63, whereas the downsized organization of 30 members peaks at 73, and the downsized organization with ten members peaks at 83. Hence, downsizing initially disrupts the organizational performance (see also Miller et al. 2012). The organization lost experienced members and their crucial knowledge for coordinating activities.
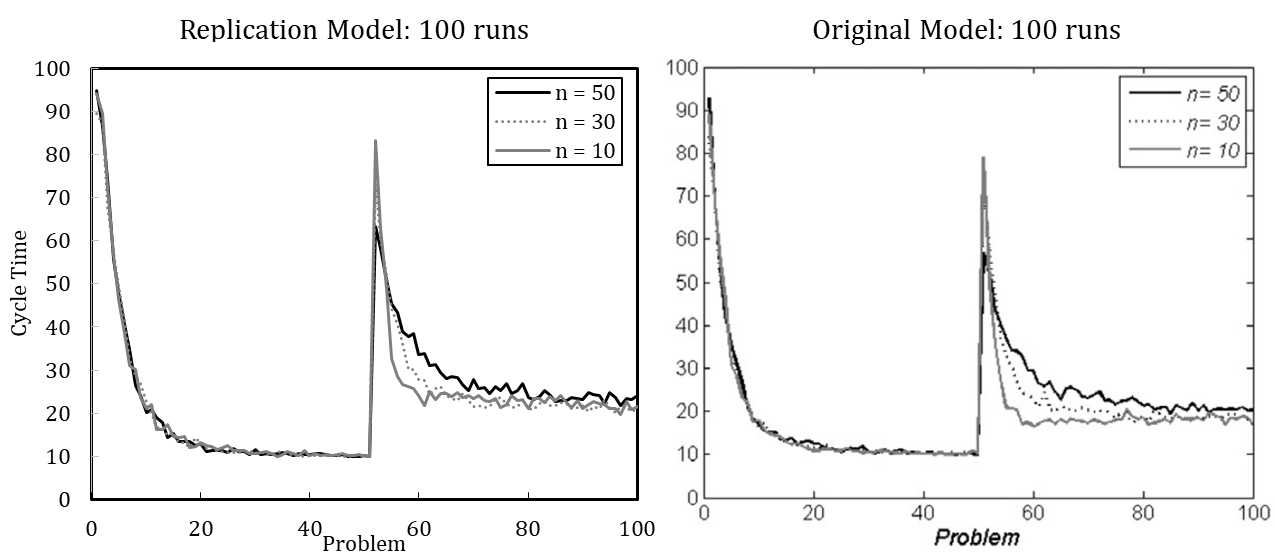
Although the averaged results of 100 simulation runs suggest that downsized organizations potentially learn more quickly in the new situation, we can make no reliable statement about which organization performs better after the change. An increased number of runs enables more detailed interpretation (see Figure 22). The heavily downsized organization with only ten remaining members shows the highest performance after the change. At first, the heavily downsized organization performs worst, but learns much faster to handle the new situation. Still, none of the organizations regains optimal performance. This suggests that smaller organizations are more agile in creating a new knowledge network among agents.
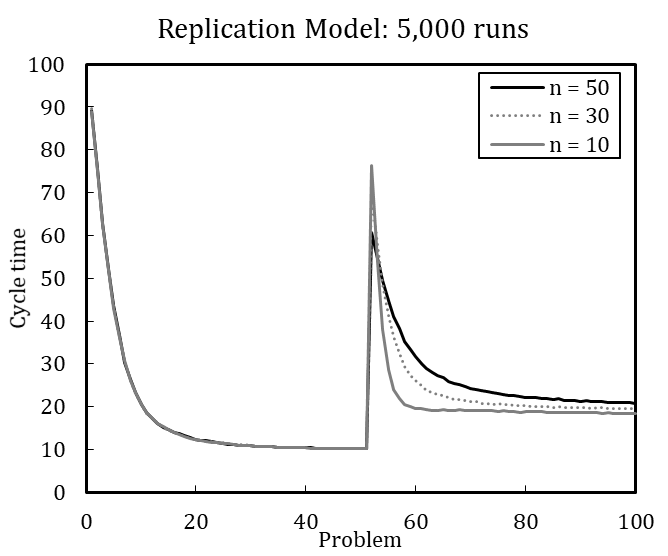
Overall, while the comparison of the results reveals some differences, both models appear to be built on identical assumptions. The generation of such similar results with two quite simple models that are built on unequal assumptions is unlikely. The complex model behavior after problem changes and downsizing is qualitatively equal. The results instead suggest high variance that results from stochasticity in the model.
C: The value of the systematic design of experiments (DOE)
Comparing the results generated by the original and replicated model reveals slight differences. The additional simulation runs yield, when averaged, smooth graphs without outliers. The original graphs point towards more stochasticity and raising the question of statistical error. The DOE technique addresses this issue, facilitating standardized communication of the experimental design and determination of effect sizes of model parameters with established statistical methods. Here, we apply the DOE technique to improve our understanding of the replicated model and to illustrate the value of the DOE technique for model evaluation.
Definition of the factorial design
DOE is appropriate for systematically exploring diverse parameter settings ( Lorscheid et al. 2012). The replicated experiments are based on selected parameter variations. The factorial design, as applied in the following, predefines the varied parameter settings. A 3k factorial design is also chosen to incorporate the parameter settings used by Miller et al. (2012). Table 8 lists the selected parameters and their corresponding factor levels.
| Factor | Factor level range | Factor levels | Representation |
| Agents (\(n\)) | [10, 50] | [10, 30, 50] | [-, 0, +] |
| Awareness (\(a\)) | [0, 10] | [1, 5, 10] | [-, 0, +] |
| Transactive memory probability (\(p_t\)) | [0, 1] | [0.25, 0.5, 0.75] | [-, 0, +] |
| Declarative memory probability (\(p_d\)) | [0, 1] | [0.25, 0.5, 0.75] | [-, 0, +] |
| Declarative memory capacity (\(w_d\)) | [1, 50] | [1, 25, 50] | [-, 0, +] |
This setting excludes a control variable, the number of tasks in a problem (\(k =\) 10) is held constant. The dependent variable is cycle time. For a full overview of the classification of the variables as applied, see Appendix A. The cycle time is measured for each problem instance. Since the modeled organizations face several consecutive problems, the resulting cycle time is dynamic. To incorporate dynamic behavior over time, we conduct our analysis in discrete steps according to the number of problems.
Determining an appropriate number of simulation runs (In reduced form, Tables 9 and 10 are already discussed in Section 6 of the main text. For readability and to pro- vide a complete presentation of all examined design points, we reproduce the full tables and some discussion here in the Appendix.)
The simulation model uses stochasticity, which demands to determine the error variance. Determining the error variance supports the choice of an appropriate number of simulation runs for the experiments. Disclosure of the error variance also enhances the credibility of reported results and allows the inclusion of stochastically induced error in model evaluation. The factorial design defines three design points with low (L), medium (M), and high (H) factor levels, as highlighted in Table 9. The design points reflect the applied settings to estimate the number of simulation runs needed to produce sufficiently robust results.
| Design Points | Factors | Representation | ||||
| n | a | pt | pd | wd | ||
| L | 10 | 1 | 0.25 | 0.25 | 1 | Low factor levels |
| M | 30 | 5 | 0.5 | 0.5 | 25 | Medium factor levels |
| H | 50 | 10 | 0.75 | 0.75 | 50 | High factor levels |
Table 10 shows the mean values and coefficients of variation for the design points H, M, and L. We measured cycle time at five selected steps during the simulation runs, when the problems (P) 1, 25, 51, 75, and 100 are solved, to account for the dynamic characteristic of the dependent variable.[33] The coefficient of variation (\(c_v\)) is calculated as the standard deviation (\(\sigma\)) divided by the arithmetic mean (\(\mu\)) of a specific number of runs (Lorscheid et al. 2012). The results in Table 10 come from numbers of simulation runs ranging between 10 and 10,000. The coefficients of variation stabilize with an increasing number of runs up to about 5,000 runs; the mean values and coefficients of variation change only slightly from 5,000 to 10,000 runs. We therefore conclude that 5,000 runs are sufficient to produce robust results.
| Design points and dependent variable | Number of runs | ||||||||
| 10 | 50 | 100 | 500 | 1000 | 5000 | 10000 | |||
| Design point L | |||||||||
| Cycle time (P1) | \(\mu\) | 78.60 | 84.38 | 84.10 | 80.94 | 80.83 | 81.69 | 81.62 | |
| \(c_v\) | 0.28 | 0.32 | 0.31 | 0.29 | 0.29 | 0.31 | 0.31 | ||
| Cycle time (P25) | \(\mu\) | 10.00 | 10.16 | 10.08 | 10.24 | 10.14 | 10.15 | 10.15 | |
| \(c_v\) | 0.00 | 0.11 | 0.08 | 0.27 | 0.20 | 0.17 | 0.16 | ||
| Cycle time (P51) | \(\mu\) | 70.20 | 58.88 | 55.67 | 54.43 | 52.12 | 53.71 | 53.82 | |
| \(c_v\) | 0.33 | 0.33 | 0.33 | 0.30 | 0.31 | 0.30 | 0.30 | ||
| Cycle time (P75) | \(\mu\) | 40.30 | 43.82 | 43.26 | 43.03 | 41.96 | 42.02 | 41.94 | |
| \(c_v\) | 0.13 | 0.25 | 0.26 | 0.30 | 0.29 | 0.28 | 0.28 | ||
| Cycle time (P100) | \(\mu\) | 38.00 | 39.04 | 40.03 | 38.39 | 38.41 | 38.44 | 38.62 | |
| \(c_v\) | 0.20 | 0.32 | 0.29 | 0.28 | 0.27 | 0.28 | 0.28 | ||
| Design point M | |||||||||
| Cycle time (P1) | \(\mu\) | 95.80 | 89.44 | 88.19 | 90.15 | 88.61 | 87.98 | 87.86 | |
| \(c_v\) | 0.24 | 0.29 | 0.32 | 0.30 | 0.31 | 0.31 | 0.31 | ||
| Cycle time (P25) | \(\mu\) | 10.00 | 10.40 | 10.26 | 10.30 | 10.39 | 10.29 | 10.27 | |
| \(c_v\) | 0.00 | 0.19 | 0.14 | 0.19 | 0.22 | 0.20 | 0.20 | ||
| Cycle time (P51) | \(\mu\) | 59.50 | 59.04 | 57.36 | 58.82 | 59.00 | 58.43 | 58.32 | |
| \(c_v\) | 0.31 | 0.28 | 0.31 | 0.32 | 0.33 | 0.32 | 0.32 | ||
| Cycle time (P75) | \(\mu\) | 30.30 | 30.32 | 28.98 | 28.00 | 28.42 | 28.63 | 28.49 | |
| \(c_v\) | 0.22 | 0.34 | 0.35 | 0.36 | 0.39 | 0.38 | 0.38 | ||
| Cycle time (P100) | \(\mu\) | 19.20 | 22.08 | 22.77 | 23.03 | 23.14 | 22.97 | 22.95 | |
| \(c_v\) | 0.26 | 0.46 | 0.43 | 0.42 | 0.41 | 0.41 | 0.41 | ||
| Design point H | |||||||||
| Cycle time (P1) | \(\mu\) | 90.50 | 86.90 | 87.83 | 88.40 | 89.84 | 89.54 | 89.52 | |
| \(c_v\) | 0.26 | 0.37 | 0.34 | 0.31 | 0.31 | 0.31 | 0.31 | ||
| Cycle time (P25) | \(\mu\) | 10.00 | 10.14 | 10.07 | 10.39 | 10.41 | 10.24 | 10.26 | |
| \(c_v\) | 0.00 | 0.10 | 0.07 | 0.33 | 0.31 | 0.21 | 0.21 | ||
| Cycle time (P51) | \(\mu\) | 69.00 | 61.02 | 61.72 | 60.86 | 61.75 | 61.58 | 61.69 | |
| \(c_v\) | 0.25 | 0.31 | 0.30 | 0.32 | 0.33 | 0.32 | 0.33 | ||
| Cycle time (P75) | \(\mu\) | 13.90 | 14.58 | 14.03 | 13.80 | 13.85 | 13.63 | 13.66 | |
| \(c_v\) | 0.47 | 0.43 | 0.39 | 0.39 | 0.40 | 0.38 | 0.38 | ||
| Cycle time (P100) | \(\mu\) | 10.90 | 10.72 | 10.48 | 10.80 | 10.96 | 10.89 | 10.86 | |
| \(c_v\) | 0.11 | 0.15 | 0.11 | 0.25 | 0.26 | 0.24 | 0.23 | ||
With large error variance detected for 100 simulation runs, results averaged over 100 runs or fewer should be carefully interpreted. Given the design point H and the cycle time of the twenty-fifth problem, the coefficient of variation is 0.07 for 100 runs and 0.21 for 5,000 runs, which is a substantial difference. A quantitative evaluation of experimental results based on 100 averaged runs is thus imprecise and error-prone compared to an assessment based on 5,000 or more simulation runs.
The results confirm the expected values of cycle time as determined analytically (see Appendix D). The analytically calculated cycle time for the first problem (P1) and a small organization (\(n =\) 10) is 82.00. The simulated average cycle time over 10,000 runs is 81.62 for a small organization (design point L). These results are approximately equal. Such an approximate “numerical identity” is also found for medium-sized and large organizations, with expected cycle time compared to simulated cycle time of 88.00 to 87.86 and 89.20 to 89.52, respectively. This offers further evidence that the replicated model is implemented correctly.
An investigation of model-induced stochasticity
The relatively high error variance for simulation runs explains the deviations identified between the replicated and original results, illustrated in the example of experiment 2 (see Appendix B). A deviation in terms of cycle time is particularly visible around the first problem-solving instances. We investigate this deviation statistically.
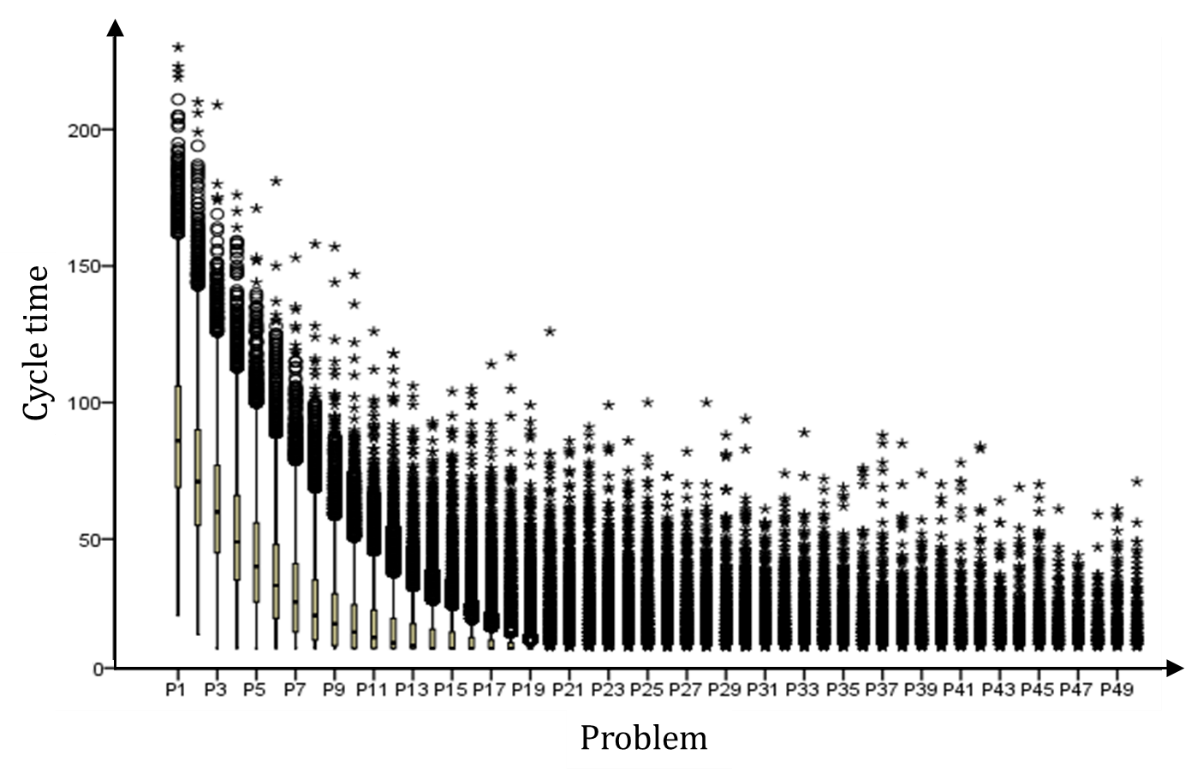
Figure 23 depicts boxplots of the resulting cycle times for experiment 2 performed with the default parameter setting (\(p_d =\) 0.5) over 5,000 simulation runs. An overview of the corresponding descriptive statistics is given in Table 11. The results are broadly scattered, as expected. Variance is limited to the lower bound by the minimum cycle time (10). The median values of the learning curves approximate this lower bound over time, but outliers still occur above the threshold value of the minimum cycle time. This skews the individual distributions (see Table 11).
For problem 10, the 25% quantile cycle time is 10, the median cycle time is 16, and the 75% quantile cycle time is 26 (see Table 11). Consequently, for half of the simulation runs, the resulting cycle time is in a wide range between 10 and 26. The other 50% of results deviate even more, suggesting that divergence between the original and replicated results could be caused by high stochasticity, particularly due to the relative low number of performed simulation runs.
| Problem | N | Mean | Median | Std. Dev. | Skewness | Min. | Max. | Percentile (25) | Percentile (50) | Percentile (75) |
| P1 | 5000 | 89.42 | 86.00 | 27.67 | 0.65 | 22 | 230 | 69 | 86 | 106 |
| P2 | 5000 | 74.26 | 71.00 | 26.27 | 0.66 | 15 | 210 | 55 | 71 | 90 |
| P3 | 5000 | 62.24 | 60.00 | 24.62 | 0.62 | 10 | 209 | 45 | 60 | 77 |
| P4 | 5000 | 52.03 | 49.00 | 23.54 | 0.75 | 10 | 176 | 35 | 49 | 66 |
| P5 | 5000 | 43.05 | 40.00 | 21.80 | 0.87 | 10 | 171 | 27 | 40 | 56 |
| P6 | 5000 | 36.28 | 33.00 | 20.11 | 1.03 | 10 | 181 | 21 | 33 | 48 |
| P7 | 5000 | 30.86 | 27.00 | 18.38 | 1.18 | 10 | 153 | 16 | 27 | 41 |
| P8 | 5000 | 26.34 | 22.00 | 16.55 | 1.42 | 10 | 158 | 13 | 22 | 35 |
| P9 | 5000 | 23.34 | 19.00 | 15.03 | 1.66 | 10 | 157 | 11 | 19 | 30 |
| P10 | 5000 | 20.57 | 16.00 | 13.55 | 1.96 | 10 | 147 | 10 | 16 | 26 |
| P11 | 5000 | 18.90 | 14.00 | 12.23 | 2.02 | 10 | 126 | 10 | 14 | 24 |
| P12 | 5000 | 17.51 | 12.00 | 11.43 | 2.38 | 10 | 118 | 10 | 12 | 21 |
| P13 | 5000 | 16.10 | 11.00 | 10.16 | 2.58 | 10 | 106 | 10 | 11 | 19 |
| P14 | 5000 | 15.21 | 10.00 | 9.47 | 2.74 | 10 | 93 | 10 | 10 | 17 |
| P15 | 5000 | 14.65 | 10.00 | 9.09 | 3.11 | 10 | 104 | 10 | 10 | 16 |
| P16 | 5000 | 13.90 | 10.00 | 8.31 | 3.53 | 10 | 105 | 10 | 10 | 14 |
| P17 | 5000 | 13.37 | 10.00 | 7.59 | 3.71 | 10 | 114 | 10 | 10 | 13 |
| P18 | 5000 | 13.02 | 10.00 | 7.32 | 4.02 | 10 | 117 | 10 | 10 | 12 |
| P19 | 5000 | 12.71 | 10.00 | 6.84 | 4.08 | 10 | 99 | 10 | 10 | 11 |
| P20 | 5000 | 12.38 | 10.00 | 6.42 | 4.54 | 10 | 126 | 10 | 10 | 10 |
| P21 | 5000 | 12.05 | 10.00 | 5.96 | 4.73 | 10 | 86 | 10 | 10 | 10 |
| P22 | 5000 | 11.93 | 10.00 | 5.98 | 5.21 | 10 | 91 | 10 | 10 | 10 |
| P23 | 5000 | 11.72 | 10.00 | 5.49 | 5.19 | 10 | 99 | 10 | 10 | 10 |
| P24 | 5000 | 11.60 | 10.00 | 5.31 | 5.27 | 10 | 86 | 10 | 10 | 10 |
| P25 | 5000 | 11.44 | 10.00 | 5.10 | 5.76 | 10 | 100 | 10 | 10 | 10 |
| P26 | 5000 | 11.29 | 10.00 | 4.73 | 5.51 | 10 | 73 | 10 | 10 | 10 |
| P27 | 5000 | 11.16 | 10.00 | 4.31 | 5.75 | 10 | 82 | 10 | 10 | 10 |
| P28 | 5000 | 11.04 | 10.00 | 4.24 | 6.59 | 10 | 100 | 10 | 10 | 10 |
| P29 | 5000 | 11.02 | 10.00 | 4.29 | 6.99 | 10 | 88 | 10 | 10 | 10 |
| P30 | 5000 | 10.91 | 10.00 | 4.07 | 7.15 | 10 | 94 | 10 | 10 | 10 |
| P31 | 5000 | 10.77 | 10.00 | 3.58 | 6.71 | 10 | 61 | 10 | 10 | 10 |
| P32 | 5000 | 10.76 | 10.00 | 3.62 | 7.42 | 10 | 74 | 10 | 10 | 10 |
| P33 | 5000 | 10.63 | 10.00 | 3.31 | 8.66 | 10 | 89 | 10 | 10 | 10 |
| P34 | 5000 | 10.64 | 10.00 | 3.42 | 8.10 | 10 | 72 | 10 | 10 | 10 |
| P35 | 5000 | 10.58 | 10.00 | 3.14 | 8.19 | 10 | 69 | 10 | 10 | 10 |
| P36 | 5000 | 10.48 | 10.00 | 2.86 | 10.30 | 10 | 76 | 10 | 10 | 10 |
| P37 | 5000 | 10.46 | 10.00 | 2.99 | 11.91 | 10 | 88 | 10 | 10 | 10 |
| P38 | 5000 | 10.41 | 10.00 | 2.70 | 10.96 | 10 | 85 | 10 | 10 | 10 |
| P39 | 5000 | 10.38 | 10.00 | 2.48 | 10.21 | 10 | 74 | 10 | 10 | 10 |
| P40 | 5000 | 10.38 | 10.00 | 2.58 | 10.48 | 10 | 70 | 10 | 10 | 10 |
| P41 | 5000 | 10.31 | 10.00 | 2.46 | 13.28 | 10 | 78 | 10 | 10 | 10 |
| P42 | 5000 | 10.27 | 10.00 | 2.37 | 15.05 | 10 | 84 | 10 | 10 | 10 |
| P43 | 5000 | 10.26 | 10.00 | 2.03 | 12.06 | 10 | 64 | 10 | 10 | 10 |
| P44 | 5000 | 10.23 | 10.00 | 1.94 | 13.57 | 10 | 69 | 10 | 10 | 10 |
| P45 | 5000 | 10.26 | 10.00 | 2.29 | 13.40 | 10 | 70 | 10 | 10 | 10 |
| P46 | 5000 | 10.19 | 10.00 | 1.73 | 13.12 | 10 | 61 | 10 | 10 | 10 |
| P47 | 5000 | 10.18 | 10.00 | 1.62 | 11.98 | 10 | 44 | 10 | 10 | 10 |
| P48 | 5000 | 10.15 | 10.00 | 1.47 | 14.60 | 10 | 59 | 10 | 10 | 10 |
| P49 | 5000 | 10.20 | 10.00 | 2.01 | 14.13 | 10 | 61 | 10 | 10 | 10 |
| P50 | 5000 | 10.16 | 10.00 | 1.76 | 16.72 | 10 | 71 | 10 | 10 | 10 |
A slight effect of declarative memory was observed in the experiments with the replicated model but not with the original. This deviation is likely due to the illustrated model stochasticity.
Calculated factor effects and their dynamic properties
Effect sizes indicate the influence of the independent variables on the dependent variable, cycle time. Cycle time varies among the discrete problem-solving instances and depends on the number of problems solved over time. This dependency is considered in calculating the factor effect sizes for each problem.[34]
Figure 24 shows the effect sizes for each factor over 100 problem-solving instances and includes a problem change once organizations have solved the fiftieth problem. The calculation is based on the 1,215,000 simulation runs resulting from the full DOE setting. [35] The effect sizes are standardized beta coefficients, and the coefficients indicate the negative and positive effects of the factors on the dependent variable. The graph thus shows in which situation a rather high or low level of a factor increases or decreases cycle time.
The number of agents has a positive effect on cycle time. More agents (\(n\)) in an organization thus increases cycle time with a varying effect size over the number of solved problems. The effect size peaks at 0.37 in the seventh problem-solving instance and after that declines. The problem change again increases the effect size to 0.27. However, in the long run, the effect size of organization size approximates zero. This result indicates that small organizations are more agile and outperform larger ones in changing environments.
The effect of agents' updating probability of transactive memory (\(p_t\)) moves contrary to the effect of (\(n\)), and the most substantial effects are negative. High updating probability of agents’ transactive memory decreases the cycle time. The peak effect size (0.48) is observed for the fifth problem-solving instance, peaking again shortly after the problem changes (0.27). The cognitive capability of agents to learn who knows what in the organization is consequently crucial to reduce cycle time, as observed in experiment 1 (see Appendix B). Moreover, the transactive memory updating probability has a significant effect after a problem change; higher cognitive capabilities by agents might compensate for an increase in organizational size.
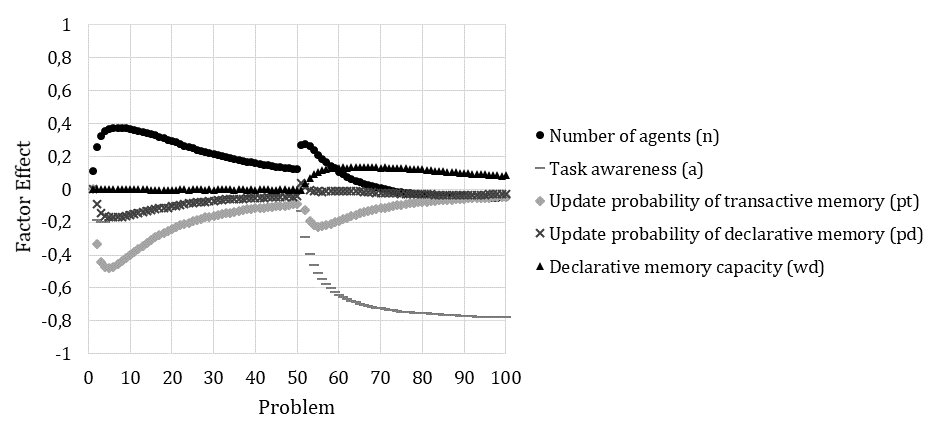
The effect of agents' updating probability of declarative memory (\(p_d\)) is similar to but weaker than the impact of transactive memory until the problem changes. After the problem change, the effect size increases to a marginal value of 0.04 but returns into slightly negative territory once the organization has solved the new problem three times. This supports the results of experiment 2 observed for the replicated model (see Appendix B). Declarative memory capacity (\(w_d\)) does not have an effect until the problem changes, when the effect size increases to 0.14; hence, higher cognitive capacity in terms of agents' declarative memory reduces organizational performance.
Higher task awareness by agents (\(a\)) reduces cycle time. The effect is already strong for the first fifty problem-solving instances, peaking at -0.20. The effect becomes still more substantial after a problem change when agents who can discern many tasks avoid taking actions guided by misleading declarative memory. Unlike the other factors, the influence of task awareness on cycle time continuously increases. Over the long run, the effect size approximates -0.80, in line with the observations of experiment 7 (see Appendix B).
Overall, the effect sizes support the observations from the discrete experiments. The standardized linear regression coefficients show dynamic model behavior, including for the scenario of a problem change. The effects of agents' individual cognitive properties differ before and after an organization faces a change in problem, suggesting further investigation of more volatile scenarios might yield valuable insights. Besides, some factors and their effects might compensate for or reinforce each other. The following section considers such interaction effects.
Interaction effects of model parameters
Factors might affect the dependent variable differently depending on the state of other factors. One parameter might moderate the effect size of another parameter. Therefore, we analyze interaction effects among factors based on linear regression. Table 12 depicts the main effects and two-way interaction effects of the model parameters, measured for problem-solving instances 10 and 60, cases at which the previous analysis indicated particularly strong effects. This selection of cases enables comparison of interaction effects before and after a problem change.
| Cycle Time (P10) | Agents (\(n\)) | Awareness (\(a\)) | Transactive memory probability (\(p_t\)) | Declarative memory probability (\(p_d\)) | Declarative memory capacity (\(w_d\)) |
| Agents (\(n\)) | 0.366 | -0.072 | -0.204 | 0.064 | 0.000 |
| Awareness (\(a\)) | -0.139 | 0.000 | 0.133 | 0.000 | |
| Transactive memory probability (\(p_t\)) | -0.402 | -0.007 | 0.000 | ||
| Declarative memory probability (\(p_d\)) | -0.155 | 0.000 | |||
| Declarative memory capacity | 0.000 | ||||
| Cycle Time (P60) | Agents (\(n\)) | Awareness (\(a\)) | Transactive memory probability (\(p_t\)) | Declarative memory probability (\(p_d\)) | Declarative memory capacity (\(w_d\)) |
| Agents (\(n\)) | 0.127 | 0.118 | -0.057 | 0.002 | -0.023 |
| Awareness (\(a\)) | -0.625 | -0.057 | -0.007 | -0.007 | |
| Transactive memory probability (\(p_t\)) | -0.202 | -0.008 | 0.010 | ||
| Declarative memory probability (\(p_d\)) | -0.011 | 0.022 | |||
| Declarative memory capacity (\(w_d\)) | 0.130 |
The performance of an organization that has solved ten recurrent problems is predominantly affected by the number of agents in the organization and their transactive memory. On the one hand, a higher number of agents (\(n\)) increases cycle time, while, on the other hand, higher updating probability of transactive memory (\(p_t\)) decreases the cycle time. The slight interaction effect (-0.204) shows that these effects are dependent; a proportional increase in both factor levels would reduce cycle time because the interaction effect is negative. The lower performance of bigger organizations can be compensated by improved cognitive capabilities of their agents, specifically their transactive memory.
A slight interaction effect (0.133) between task awareness and declarative memory updating probability supports the assumption that low task awareness might be substituted by agents who frequently update their declarative memory.[36]
After a problem change, in the sixtieth problem-solving instance, the previously discussed interaction effects largely diminish, except for a marginal increase in the interaction effect between the number of agents and their task awareness. The performance of organizations that handle a problem change is primarily positively affected (that is, cycle time is reduced) by high task awareness and high update rate of agents' transactive memory. Performance is reduced by an increased number of agents and an increased declarative memory capacity.
These interaction effects support previous observations. The effect sizes help to understand the fundamental model behavior and simulation results. The error variance matrix supports in the estimation of an appropriate number of simulation runs of the replicated model to facilitate robust results. Thereby, we provided an demonstration of the value of the DOE for agent-based model analyses.
D: Analytical calculation of expected simulation results
Reformulating the conceptual model description fostered our understanding of the model. The simple design allows a logical derivation of the organizational behavior that results for the first solved problem and further, an analytical determination of the expected cycle time for that problem. For subsequent problem-solving processes, the complexity of the modeled behavior increases because agents learn, which affects their search behavior.
In the very first problem-solving instance, agents are inexperienced and have to use a random search. Given (\(n =\) 10) agents and a problem comprising (\(k =\) 10) different tasks, each agent has to perform a task. Each performed task increases cycle time, so the cycle time is at least 10. The agent that performs the last task does not need to search for other agents, because the problem has been solved. The other nine agents have to search for skilled colleagues to handover the problem. The probability that a searching agent approaches a qualified colleague by random search depends on the number of agents in the organization (\(n\)) and the number of different tasks (\(k\)) in a problem. In the given random search setting, described as an urn model with replacement, the probability a searching agent will approach a skilled colleague is 1/9, and the reciprocal value 9/1 represents the expected search costs. Successful searches of the nine agents result in a task handover to an agent who performs the necessary task, which is accounted for in the minimum cycle time of the ten performed tasks. The cycle time for the first problem-solving process of a small organization (\(n =\) 10) is thus calculated as follows:
| $$\textit{Expected cycle time}(n = 10; k=10)=10 + 9 \ast \frac{9}{1} - 9 = 82.00$$ |
Another applied parameter setting reflects a medium-sized organization (\(n =\) 30). The setting affects agents' search success probabilities since the necessary skills are uniformly distributed among agents. Thus, three agents have redundant skills in an organization of 30 agents. The expected cycle time is higher in comparison to a small organization, because the searching agent has a higher probability of approaching agents with identical skills:
| $$\textit{Expected cycle time}(n = 30; k=10)=10 + 9 \ast \frac{29}{3} - 9 = 88.00$$ |
A large organization is modeled by the default parameter setting (\(n =\) 50). The expected cycle time for the first problem only slightly increases in comparison to the medium-sized organization:
| $$\textit{Expected cycle time}(n = 50; k=10)=10 + 9 \ast \frac{49}{5} - 9 = 89.20$$ |
Presupposed that each agent has one particular skill and that the skills are uniformly distributed among the agents in the organization, a general formula allows the calculation of the expected cycle time for the first problem-solving instance for any parameter setting:
| $$\textit{Expected cycle time}(n,k)=k + \Bigl( (k-1)\ast \frac{n-1}{\frac{n}{k}}-(k-1) \Bigr)$$ |
The calculation of the cycle time for the first problem-solving process is helpful in evaluating pretest results produced with the re-implemented model. Moreover, the analytically determined cycle times help to verify the replicated and original results.
E: Explaining unusual routines: Insights into agents' knowledge base
Analysis of the model and experimental results yield insights into how routines emerge from individuals and their cognitive properties. Nevertheless, some questions remain unanswered. How do unusual routines form? Which recurrent patterns of actions can emerge? Downsizing has been analyzed, but how are routines affected if organizations merge? What happens if organizations face more frequent problem changes? Are organizations even capable of forming routines in volatile environments? This section addresses these questions.
Organizations may be unable to regain their optimal performance after a problem change. In this case, organizational performance is predominantly affected by individuals' task awareness and declarative memory. Presumably, these are essential levers to control the formation of unusual routines, which reduce organizational performance. In this model, organizational behavior results from individual behavior. During a simulation run, agents learn. In their declarative memory, agents store which task follows the task they accomplished. They retrieve information from this memory whenever they are not aware of the next task, behaving in accordance with their declarative memory. Therefore, the habits that agents acquire over time are reflected in their knowledge base.
The following investigation aims to analyze agents’ developed knowledge base, measuring the amount and correctness of information stored in their declarative memory. The average agent knowledge base is representative because the agents are homogenous.[37] The analysis focuses on the one-hundredth problem-solving instance to ensure that organizational performance has re-stabilized after the change in the fiftieth problem instance. In other words, the agents have been given a decent chance to learn how to handle the new problem.
Table 13 shows the results of the investigation of agents’ knowledge base. Three types of organizations are investigated, comprising agents with low, medium, and high task awareness. The cycle time for the hundredth problem-solving instance is depicted, as well as the average experience of the agents and their behavior.
| Agents with low task awareness (a = 1) | Agents with medium task awareness (a = 5) | Agents with high task awareness (a = 9) | |
| Cycle Time | 38.79 | 21.56 | 10.90 |
| Experienced | 96.24% | 89.66% | 77.54% |
| Inexperienced | 3.76% | 10.34% | 22.46% |
| Habit: necessary action | 16.30% | 21.38% | 40.78% |
| Habit: obsolete action | 41.06% | 40.08% | 12.46% |
| Habit: unnecessary action | 42.64% | 38.54% | 46.76% |
Regardless of agents' task awareness, most agents gained experience. For this analysis, the number of agents in the organizations is held constant at (\(n =\) 50). The results show that most agents are involved in the problem-solving process, even though the organizations only require (\(n =\) 10) agents to solve the (\(k = \)10) tasks related to a problem. This offers evidence that the knowledge of routines is highly distributed among agents.
Agents gain the most experience if their task awareness is rather low. About 96% of agents with low task awareness (\(a =\) 1) gain experience compared to about 78% of agents with high task awareness (\(a =\) 9). An agent that cannot recognize what to do next always searches randomly for help from others. This drives the number of interactions among different agents. Therefore, most agents are involved in the problem-solving processes and gain experience.
Agents that gain experience can also develop habits. Agents who are unaware of what to do next draw on their experience about what they have done in similar situations. They then behave as suggested by their declarative memory. However, their habits can be more or less appropriate, given the job at hand. Three types of habits are identified: (1) agents behave appropriately given the problem and perform a necessary action; (2) agents behave inappropriately because they perform an action that has become obsolete since the problem changed; and (3) agents behave inappropriately because they learned something wrong and perform an unnecessary action.
Although most agents are experienced, their habits overall are inappropriate for the problem, even those aware of 90% of the tasks (\(a =\) 9). One might expect, in this case, for agents’ habits to also match 90% of their situations at hand. However, agents’ habits only match the problem at hand in 40.78% of cases, as reflected in their declarative memories. Nevertheless, agents with high task awareness efficiently unlearn obsolete behavior (reduced to 12.46% of actions, compared to 41.06% of actions by agents with low task awareness). Notably, too, the habits of agents with low task awareness (16.30%) outperform their awareness, as they are only aware of 10% of the tasks (\(a =\) 1). Experienced agents are likely to develop habits (42.64%, 38.54%, and 46.76%, respectively, for agents with low, medium, and high task awareness) that neither match the initial nor the actual problem.
Most habits can lead to unnecessary activities for a given problem. Organizations are thus often enmeshed into special subroutines, reducing their performance. Indeed, agents with high task awareness seldom rely on their declarative memory. In contrast, agents with low task awareness commonly consult their declarative memory. Overall, 83.70% of agents perform unnecessary (42.64%) or obsolete (41.06%) actions, increasing the expected average cycle time proportionally to 10 \(\times\) 100%/(100% - 83.70%) \(=\) 61.34. Yet the average cycle time is only 38.79, indicating that interactions among agents prevent the performance of unnecessary tasks.[38]
To sum up, agents' habits alone cannot explain organizational performance. Organizations need personnel with high task awareness to mitigate the emergence of unusual routines. Agents with low task awareness have a high potential to develop unusual routines when facing change. In such an organization, experienced agents follow habits that are inappropriate to the organization's goal, although the enactment of their inappropriate habits is mitigated through interactions among individuals.
F: The path dependency of the development of organizational routines
In this experiment, the organization faces 100 different problems that are randomly generated, except for the very first problem. Although the simulated organization solves 100 distinct problems, the original action pattern that matches the very first problem is still detectable (see Table 14).
| Subsequent performed tasks | |||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| Performed task | |||||||||||
| 0 | 0.00 | 1.20 | 1.07 | 1.00 | 1.08 | 1.05 | 1.06 | 1.08 | 1.04 | 1.01 | |
| 1 | 1.02 | 0.00 | 1.24 | 1.08 | 1.04 | 1.15 | 1.05 | 1.14 | 1.15 | 1.05 | |
| 2 | 1.04 | 1.10 | 0.00 | 1.28 | 1.14 | 1.11 | 1.10 | 1.07 | 1.05 | 1.13 | |
| 3 | 1.04 | 1.04 | 1.07 | 0.00 | 1.30 | 1.09 | 1.15 | 1.12 | 1.14 | 1.10 | |
| 4 | 1.04 | 1.08 | 1.07 | 1.05 | 0.00 | 1.38 | 1.09 | 1.06 | 1.05 | 1.13 | |
| 5 | 1.11 | 1.09 | 1.09 | 1.13 | 1.04 | 0.00 | 1.33 | 1.14 | 1.09 | 1.13 | |
| 6 | 1.10 | 1.11 | 1.09 | 1.07 | 1.11 | 1.01 | 0.00 | 1.37 | 1.05 | 1.15 | |
| 7 | 1.07 | 1.10 | 1.11 | 1.09 | 1.10 | 1.11 | 0.09 | 0.00 | 1.35 | 1.10 | |
| 8 | 1.09 | 1.14 | 1.09 | 1.12 | 1.08 | 1.10 | 1.05 | 1.02 | 0.00 | 1.34 | |
| 9 | 1.12 | 1.10 | 1.13 | 1.15 | 1.15 | 1.12 | 1.15 | 1.16 | 1.03 | 0.00 | |
References
ADLER, P. S., Goldohas, B. & Levine, D. I. (1999). Flexibility versus efficiency? A case study of model changeovers in the Toyota production system. Organization Science, 10(1), 43–68. [doi:10.1287/orsc.10.1.43]
AGGARWAL, V. A., Posen, H. E. & Workiewicz, M. (2017). Adaptive capacity to technological change: A microfoundational approach. Strategic Management Journal, 38(6), 1212–1231. [doi:10.1002/smj.2584]
ANAND, G., Gray, J. & Siemsen, E. (2012). Decay, shock, and renewal: Operational routines and process entropy in the pharmaceutical industry. Organization Science, 23(6), 1700–1716. [doi:10.1287/orsc.1110.0709]
ANDRADE, G., Mitchell, M. & Stauord, E. (2001). New evidence and perspectives on mergers. Journal of Economic Perspectives, 15(2), 103–120. [doi:10.1257/jep.15.2.103]
ARGOTE, L. (2011). Organizational learning research: Past, present and future. Management Learning, 42(4), 439– 446. [doi:10.1177/1350507611408217]
AXELROD, R. (1997). Advancing the art of simulation in the social sciences. Complexity, 3(2), 16–22.
BENA, J. & Li, K. (2014). Corporate innovations and mergers and acquisitions. The Journal of Finance, 69(5), 1923–1960. [doi:10.1111/jofi.12059]
BIESENTHAL, C., Gudergan, S. & Ambrosini, V. (2019). The role of ostensive and performative routine aspects in dynamic capability deployment at different organizational levels. Long Range Planning, 52(3), 350–365. [doi:10.1016/j.lrp.2018.03.006]
BILLINGER, S., Becker, M. & Gorski, W. (2014). Stability of organizational routines and the role of authority. Paper presented at the DRUID Society Conference, Copenhagen.
BOGNER, W. C. & Barr, P. S. (2000). Making sense in hypercompetitive environments: A cognitive explanation for the persistence of high velocity competition. Organization Science, 11(2), 212–226. [doi:10.1287/orsc.11.2.212.12511]
BRAUER, M. & Laamanen, T. (2014). Workforce downsizing and firm performance: An organizational routine perspective. Journal of Management Studies, 51(8), 1311–1333. [doi:10.1111/joms.12074]
CARAYANNIS, E. G., Grigoroudis, E., Del Giudice, M., Della Peruta, M. R. & Sindakis, S. (2017). An exploration of contemporary organizational artifacts and routines in a sustainable excellence context. Journal of Knowledge Management, 21(1), 35–56. [doi:10.1108/jkm-10-2015-0366]
DAVIS, J. P., Eisenhardt, K. M. & Bingham, C. B. (2007). Developing theory through simulation methods. Academy of Management Review, 32(2), 480–499. [doi:10.5465/amr.2007.24351453]
DAWID, H., Harting, P., van der Hoog, S. & Neugart, M. (2019). Macroeconomics with heterogeneous agent models: Fostering transparency, reproducibility and replication. Journal of Evolutionary Economics, 29(1), 467–538. [doi:10.1007/s00191-018-0594-0]
DENRELL, J. & Powell, T. C. (2016). Dynamic capability as a theory of competitive advantage: Contributions and scope conditions. In D. J. Teece, & S. Heaton (Eds.), The Oxford Handbook of Dynamic Capabilities. Oxford: Oxford University Press. [doi:10.1093/oxfordhb/9780199678914.013.007]
DONKIN, E., Dennis, P., Ustalakov, A., Warren, J. & Clare, A. (2017). Replicating complex agent based models, a formidable task. Environmental Modelling & Software, 92, 142–151. [doi:10.1016/j.envsoft.2017.01.020]
EDMONDS, B. & Moss, S. (1984). From KISS to KIDS – An ’anti-simplistic’ modelling approach. In P. Davidsson, B. Logan & K. Takadama (Eds.), Multi-Agent and Multi-Agent-Based Simulation. Joint Workshop MABS 2004, New York, NY, USA, July 19, 2004. Revised Selected Papers, (pp. 130–144). Berlin/Heidelberg: Springer. [doi:10.1007/978-3-540-32243-6_11]
FACHADA, N., Lopes, V. V., Martins, R. C. & Rosa, A. C. (2017). Model-independent comparison of simulation output. Simulation Modelling Practice and Theory, 72, 131–149. [doi:10.1016/j.simpat.2016.12.013]
FARJOUN, M. (2010). Beyond dualism: Stability and change as a duality. Academy of Management Review, 35(2), 202–225. [doi:10.5465/amr.35.2.zok202]
FELDMAN, M. S. & Pentland, B. T. (2003). Reconceptualizing organizational routines as a source of flexibility and change. Administrative Science Quarterly, 48(1), 94–118. [doi:10.2307/3556620]
FELDMAN, M. S. & Rafaeli, A. (2002). Organizational routines as sources of connections and understandings. Journal of Management Studies, 39(3), 309–331. [doi:10.1111/1467-6486.00294]
GAO, D., Squazzoni, F. & Deng, X. (2018). The role of cognitive artifacts in organizational routine dynamics: An agent-based model. Computational and Mathematical Organization Theory, 24(4), 473–499. [doi:10.1007/s10588-018-9263-y]
GILES, J. (2006). The trouble with replication. Nature, 442(7101), 344–347 [doi:10.1038/442344a]
GRIMM, V., Berger, U., Bastiansen, F., Eliassen, S., Ginot, V., Giske, J., Goss-Custard, J., Grand, T., Heinz, S. K., Huse, G., Huth, A., Jepsen, J. U., Jørgensen, C., Mooij, W. M., Müller, B., Pe’er, G., Piou, C., Railsback, S. F., Robbins, A. M., Robbins, M. M., Rossmanith, E., Rüger, N., Strand, E., Souissi, S., Stillman, R. A., Vabø, R., Visser, U. & DeAngelis, D. L. (2006). A standard protocol for describing individual-based and agent-based models. Ecological Modelling, 198(1–2), 115–126. [doi:10.1016/j.ecolmodel.2006.04.023]
GRIMM, V., Berger, U., DeAngelis, D. L., Polhill, J. G., Giske, J. & Railsback, S. F. (2010). The ODD protocol: A review and first update. Ecological Modelling, 221(23), 2760–2768. [doi:10.1016/j.ecolmodel.2010.08.019]
GRIMM, V., Revilla, E., Berger, U., Jeltsch, F., Mooij, W. M., Railsback, S. F., Thulke, H.-H., Weiner, J., Wiegand, T. & DeAngelis, D. L. (2005). Pattern-oriented modeling of agent-based complex systems: Lessons from ecology. Science, 310(5750), 987–991 [doi:10.1126/science.1116681]
HAUKE, J., Lorscheid, I. & Meyer, M. (2017). Recent development of social simulation as reflected in JASSS between 2008 and 2014: A citation and co-citation analysis. Journal of Artificial Societies and Social Simulation, 20(1), 5: https://www.jasss.org/20/1/5.html. [doi:10.18564/jasss.3238]
HEATH, B., Hill, R. & Ciarallo, F. (2009). A survey of agent-based modeling practices (January 1998 to July 2008). Journal of Artificial Societies and Social Simulation, 12(4), 9: https://www.jasss.org/12/4/9.html.
HEIMERIKS, K. H., Schijven, M. & Gates, S. (2012). Manifestations of higher-order routines: The underlying mechanisms of deliberate learning in the context of postacquisition integration. Academy of Management Journal, 55(3), 703–726. [doi:10.5465/amj.2009.0572]
HELFAT, C. E. & Peteraf, M. A. (2009). Understanding Dynamic Capabilities: Progress Along a Developmental Path. London: Sage. [doi:10.1177/1476127008100133]
HODGSON, G. M. (2008). The concept of a routine. In M. C. Becker (Ed.), Handbook of Organizational Routines, Vol. 15. Cheltenham: Elgar
HOWARD-Grenville, J. A. (2005). The persistence of flexible organizational routines: The role of agency and organizational context. Organization Science, 16(6), 618–636 [doi:10.1287/orsc.1050.0150]
JANSSEN, M. A. (2017). The practice of archiving model code of agent-based models. Journal of Artificial Societies and Social Simulation, 20(1), 2: https://www.jasss.org/20/1/2.html. [doi:10.18564/jasss.3317]
KAHL, C. H. & Meyer, M. (2016). Constructing agent-based models of organizational routines. In D. Secchi & M. Neumann (Eds.), Agent-Based Simulation of Organizational Behavior: New Frontiers of Social Science Research, (pp. 85–107). Cham: Springer International. [doi:10.1007/978-3-319-18153-0_5]
LEGENDI, R. & Gulyas, L. (2012). Replication of the Macro ABM Model. CRISIS, working paper.
LIN, H., Chen, M. & Su, J. (2017). How management innovations are successfully implemented? An organizational routines’ perspective. Journal of Organizational Change Management, 30(4), 456–486. [doi:10.1108/jocm-07-2016-0124]
LORSCHEID, I., Berger, U., Grimm, V. & Meyer, M. (2019). From cases to general principles: A call for theory development through agent-based modeling. Ecological Modelling, 393, 153–156. [doi:10.1016/j.ecolmodel.2018.10.006]
LORSCHEID, I., Heine, B.-O. & Meyer, M. (2012). Opening the ‘black box’of simulations: Increased transparency and effective communication through the systematic design of experiments. Computational and Mathematical Organization Theory, 18(1), 22–62. [doi:10.1007/s10588-011-9097-3]
LUBATKIN, M. H., Simsek, Z., Ling, Y. & Veiga, J. F. (2006). Ambidexterity and performance in small-to medium- sized firms: The pivotal role of top management team behavioral integration. Journal of Management, 32(5), 646–672. [doi:10.1177/0149206306290712]
MIŁKOWSKI, M., Hensel, W. M. & Hohol, M. (2018). Replicability or reproducibility? On the replication crisis in computational neuroscience and sharing only relevant detail. Journal of Computational Neuroscience, 45(3), 163–172. [doi:10.1007/s10827-018-0702-z]
MILLER, K. D., Choi, S. & Pentland, B. T. (2014). The role of transactive memory in the formation of organizational routines. Strategic Organization, 12(2), 109–133. [doi:10.1177/1476127014521609]
MILLER, K. D., Pentland, B. T. & Choi, S. (2012). Dynamics of performing and remembering organizational routines. Journal of Management Studies, 49(8), 1536–1558. [doi:10.1111/j.1467-6486.2012.01062.x]
MIODOWNIK, D., Cartrite, B. & Bhavnani, R. (2010). Between replication and docking: “adaptive agents, political institutions, and civic traditions” revisited. Journal of Artificial Societies and Social Simulation, 13(3), 1: https://www.jasss.org/13/3/1.html. [doi:10.18564/jasss.1627]
MONKS, T., Currie, C. S., Onggo, B. S., Robinson, S., Kunc, M. & Taylor, S. J. (2019). Strengthening the reporting of empirical simulation studies: Introducing the STRESS guidelines. Journal of Simulation, 13(1), 55–67. [doi:10.1080/17477778.2018.1442155]
NELSON, R. R. & Winter, S. G. (1982). An Evolutionary Theory of Economic Change. Cambridge, MA: Harvard University Press.
NOSEK, B. A., Alter, G., Banks, G. C., Borsboom, D., Bowman, S. D., Breckler, S. J., Buck, S., Chambers, C. D., Chin, G., Christensen, G., Contestabile, M., Dafoe, A., Eich, E., Freese, J., Glennerster, R., Gorou, D., Green, D. P., Hesse, B., Humphreys, M., Ishiyama, J., Karlan, D., Kraut, A., Lupia, A., Mabry, P., Madon, T., Malhotra, N., Mayo-Wilson, E., McNutt, M., Miguel, E., Levy Paluck, E., Simonsohn, U., Soderberg, C., Spellman, B. A., Turitto, J., Van den Bos, G., Vazire, S., Wagenmakers, E. J., Wilson, R. & Yarkoni, T. (2015). Promoting an open research culture. Science, 348(6242), 1422–1425.
PADHI, S. S., Wagner, S. M., Niranjan, T. T. & Aggarwal, V. (2013). A simulation-based methodology to analyse production line disruptions. International Journal of Production Research, 51(6), 1885–1897. [doi:10.1080/00207543.2012.720389]
PENTLAND, B. T., Feldman, M. S., Becker, M. C. & Liu, P. (2012). Dynamics of organizational routines: A generative model. Journal of Management Studies, 49(8), 1484–1508. [doi:10.1111/j.1467-6486.2012.01064.x]
PISANO, G. P. (2015). A normative theory of dynamic capabilities: Connecting strategy, know-how, and competition. Harvard Business School Technology & Operations Mgt. Unit Working Paper, (16-036). [doi:10.2139/ssrn.2667018]
RAISCH, S., Birkinshaw, J., Probst, G. & Tushman, M. L. (2009). Organizational ambidexterity: Balancing exploitation and exploration for sustained performance. Organization Science, 20(4), 685–695. [doi:10.1287/orsc.1090.0428]
RAND, W. & Rust, R. T. (2011). Agent-based modeling in marketing: Guidelines for rigor. International Journal of Research in Marketing, 28(3), 181–193. [doi:10.1016/j.ijresmar.2011.04.002]
RAND, W. & Wilensky, U. (2006). Verification and validation through replication: A case study using Axelrod and Hammond’s ethnocentrism model. North American Association for Computational Social and Organization Sciences (NAACSOS), (pp. 1–6).
RICHARDSON, A. J. (2017). The discovery of cumulative knowledge. Accounting, Auditing & Accountability Journal, 31(2), 563–585.
RICHIARDI, M., Leombruni, R., Saam, N. J. & Sonnessa, M. (2006). A common protocol for agent-based social simulation. Journal of Artificial Societies and Social Simulation, 9(1), 15: https://www.jasss.org/9/1/15.html.
ROH, J., Turkulainen, V., Whipple, J. M. & Swink, M. (2017). Organizational design change in multinational supply chain organizations. Logistics Management, 28(4), 1078–1098. [doi:10.1108/ijlm-06-2016-0146]
SANSORES, C. & Pavón, J. (2005). Agent-based simulation replication: A model driven architecture approach. Paper presented at the MICAI 2005: Advances in Artificial Intelligence, Monterrey, Mexico. [doi:10.1007/11579427_25]
SARALA, R. M., Junni, P., Cooper, C. L. & Tarba, S. Y. (2016). A sociocultural perspective on knowledge transfer in mergers and acquisitions. Journal of Management, 42(5), 1230–1249. [doi:10.1177/0149206314530167]
SCHMIDT, S. (2009). Shall we really do it again? The powerful concept of replication is neglected in the social sciences. Review of General Psychology, 13(2), 90–100. [doi:10.1037/a0015108]
SECCHI, D. & Seri, R. (2017). Controlling for false negatives in agent-based models: A review of power analysis in organizational research. Computational and Mathematical Organization Theory, 23(1), 94–121. [doi:10.1007/s10588-016-9218-0]
SMALDINO, P. E., Calanchini, J. & Pickett, C. L. (2015). Theory development with agent-based models. Organizational Psychology Review, 5(4), 300–317. [doi:10.1177/2041386614546944]
STODDEN, V., McNutt, M., Bailey, D. H., Deelman, E., Gil, Y., Hanson, B., Heroux, M. A., Ioannidis, J. P. A. & Taufer, M. (2016). Enhancing reproducibility for computational methods. Science, 354(6317), 1240–1241. [doi:10.1126/science.aah6168]
THIELE, J. C. & Grimm, V. (2015). Replicating and breaking models: Good for you and good for ecology. Oikos, 124(6), 691–696 [doi:10.1111/oik.02170]
TYLÉN, K., Allen, M., Hunter, B. K. & Roepstoru, A. (2012). Interaction vs. observation: Distinctive modes of social cognition in human brain and behavior? A combined fMRI and eye-tracking study. Frontiers in Human Neuroscience, 6, 331. [doi:10.3389/fnhum.2012.00331]
VERGNE, J.-P. & Durand, R. (2010). The missing link between the theory and empirics of path dependence: Conceptual clarification, testability issue, and methodological implications. Journal of Management Studies, 47(4), 736–759. [doi:10.1111/j.1467-6486.2009.00913.x]
WEICK, K. E. (1989). Theory construction as disciplined imagination. Academy of Management Review, 14(4), 516-531. [doi:10.5465/amr.1989.4308376]
WHETTEN, D. A. (1989). What constitutes a theoretical contribution? Academy of Management Review, 14(4), 490-495. [doi:10.5465/amr.1989.4308371]
WILENSKY, U. & Rand, W. (2007). Making models match: Replicating an agent-based model. Journal of Artificial Societies and Social Simulation, 10(4), 2: https://www.jasss.org/10/4/2.html.
WILL, O. & Hegselmann, R. (2008). A replication that failed on the computational model in ‘Michael W. Macy and Yoshimichi Sato: Trust, cooperation and market formation in the US and Japan. Proceedings of the National Academy of Sciences, May 2002’. Journal of Artificial Societies and Social Simulation, 11(3), 3: https://www.jasss.org/11/3/3.html. [doi:10.18564/jasss.1611]
WINTER, S. G. (2013). Habit, deliberation, and action: Strengthening the microfoundations of routines and capabilities. Academy of Management Perspectives, 27(2), 120–137. [doi:10.5465/amp.2012.0124]
ZHONG, W. & Kim, Y. (2010). Using model replication to improve the reliability of agent-based models. In Inter- national Conference on Social Computing, Behavioral Modeling, and Prediction, (pp. 118–127). Cham: Springer. [doi:10.1007/978-3-642-12079-4_17]

