A Noisy Opinion Formation Model with Two Opposing Mass Media

Introduction

Social influence is a strong determinant of opinion formation. People’s opinions are influenced by those around them, such as family members, friends and acquaintances (Klofstad et al. 2013; Lazer et al. 2010; Mutz 2002). Recent studies have considered the possibility of an echo-chamber and examined if social influence occurs only among like-minded individuals (Bakshy et al. 2015; Barberá et al. 2015; Baumann et al. 2020). Research conducted over the last few decades has found that various attributes and behaviours diffuse on social networks (Christakis & Fowler 2009).

Agent-based models have become an important research tool to understand opinion formation. Agent-based models identify the rules of micro-level interactions and observe emerging macro-level outcomes. Researchers in multiple fields from sociology to physics have utilised agent-based models to comprehend how people form their opinions in societies (Castellano et al. 2009; Flache et al. 2017). In addition, researchers have incorporated a network science framework and examined how local interaction structures defined by social networks determine opinion distribution (see Meng et al. 2018 for a recent extensive investigation).

Opinions are often represented on a continuous scale. For example, one’s political position or ideology can be arranged on a one-dimensional left–right scale. Empirical studies devise and apply estimation techniques to place political actors, such as voters, in an ideological space (Barberá et al. 2015; Jessee 2009). In another example, attitudes towards specific policies can also be represented by a continuous scale. As the strength of support for a policy varies from person to person, it may require more than a dichotomous variable, for and against, to represent policy attitudes. Previous studies have proposed a continuous opinion model, such as the bounded confidence model (Deffuant et al. 2000; Hegselmann & Krause 2002).

Assimilative interaction is one tendency that has been incorporated in various opinion formation models (Axelrod 1997; Deffuant et al. 2000; Hegselmann & Krause 2002). People tend to become more agreeable when they are surrounded by those who have different opinions. Opinion formation models have assumed agents’ opinions tend to converge after interactions. This basic pattern can be understood as people minimising the dissonance created when holding different opinions (Groeber et al. 2014).

Opinion distributions demonstrate diversity. The typical character of opinion distribution is a central peak at the middle position, exemplified by people’s ideological positions on a left–right scale (Flache et al. 2017). At the same time, an existing central peak does not indicate opinion homogeneity; opinions are distributed around the centre and remain diverse. Furthermore, despite recent political polarisation, the distribution of the ideological positions of the electorate indicates a weak tendency toward bimodality, and the study does not observe separate opinion clusters in the United States (Lelkes 2016). Canonical models of continuous opinion formation do not stress these patterns. In the bounded confidence model, for example, opinions converge into several homogeneous clusters whose members do not interact beyond the boundaries of the clusters (Deffuant et al. 2000; Hegselmann & Krause 2002). If research interest lies in the analysis of the distribution of macroscopic opinions, as previously described, then this basic property of the model will not match empirical observations. In addition, a small probability of interacting with agents outside those clusters leads to a totally homogeneous state (Mäs et al. 2010). A similar pattern is also observed in discrete models of social influence (Klemm et al. 2003; Macy & Tsvetkova 2015), and a different form of social influence (Flache & Macy 2011a) or a learning rule (Banisch & Olbrich 2019) is required to maintain diversity.

A method to maintain opinion diversity without clusters not interacting with each other is to introduce errors in opinion modifications. Added noise preserves opinion heterogeneity by working against the tendency to assimilation. Some studies have confirmed that errors in opinion modifications preserve the original patterns of bounded confidence models; overly large errors dissolve existing clusters and induce a transition to disordered states (Grauwin & Jensen 2012; Kurahashi-Nakamura et al. 2016; Pineda et al. 2009). In these models, however, clusters generated by restricted interaction mainly preserve opinion heterogeneity. Another model assumes that noise becomes larger when interactions occur between similar agents (Mäs et al. 2010). The motivation to differentiate from similar individuals may be more appropriate for modelling fads such as fashion than for modelling opinion formation.

This study examined the determinants of opinion distribution under the condition that noisiness preserved opinion heterogeneity. The study employed this setting as a starting point because it can mimic the unimodal diversity observed in several opinion distributions. To this end, we expanded a model introduced in Laver (2020). This model assumes assimilative interaction in the same way as many models. However, a small intensity of assimilation is assumed, and the speed of opinion convergence becomes smaller. In addition, fixed-size errors accompany the opinion modification process and prevent the perfect convergence of opinion. The combination of weak assimilation intensity and errors preserves opinion heterogeneity. We investigated how opinion polarisation depends on system parameters when opinion heterogeneity is always preserved by a noisy process (please refer to Schweighofer et al. 2020; however, for a different aspect of polarisation, we focused on opinion heterogeneity).

An influential factor we considered in our opinion formation model was mass media. In opinion formation models, mass media are treated as external agents who interact with many agents (Galam 1997; Shibanai et al. 2001). The introduction of one mass media tends to preserve opinion diversity, despite interacting with many agents globally (Cosenza et al. 2020; González-Avella et al. 2005, 2010; Peres & Fontanari 2010, 2011; Pineda & Buendía 2015; Shibanai et al. 2001). One branch point in modelling is the number of mass media. Although earlier studies considered single mass media, some recent studies have considered the effects of multiple mass media (Mckeown & Sheehy 2006; Quattrociocchi et al. 2014; Bhat & Redner 2019). Competition between multiple mass media is a basic component of advanced democracies; therefore, we examined the effects of two mass media outlets with opposite opinions although this situation receives relatively less attention. This setting has some similarity with models that assume extremists at the edge of an opinion spectrum (Deffuant 2006; Mathias et al. 2016). Further, similar ideas were proposed early on in the context of discrete opinion models (Galam & Jacobs 2007). The study examined how zealots affect equilibrium proportions of two opposing opinions and the basin of attraction of equilibria.

Our analysis of mass media was concerned with two points. The first is the effects of mass media independent of interaction thresholds. Previous studies have reported that interaction thresholds, which prohibit interaction between agents and mass media, regulate the extent of the influence of mass media (Peres & Fontanari 2010, 2011). This study highlighted stationary states that were not frozen by thresholds, including bounded confidence. Second, analysis focused on the qualitative variations in the roles of mass media. For example, Wang et al. (2020) demonstrated that the larger effects of multiple mass media lead to smaller polarisation, whereas Mckeown & Sheehy (2006) and Bhat & Redner (2019) reported that larger effects lead to opinion polarisation. The results of this study confirmed the non-monotonic effects of mass media. In other words, one model could capture the moderation and polarisation effects of interaction with mass media.

The opinion formation model, which will be introduced in the next section, aimed to make the following contributions. First, the study introduced situations where weak conformity and errors maintained opinion diversity and examined the influence of mass media on opinion polarisation. This setting was motivated by the observation that separate opinion clusters did not frequently maintain opinion diversity. Second, investigating this situation revealed that mass media may contribute to moderation and polarisation according to the strength of their influence and may play a qualitatively different role in opinion formation.

Model

We considered a computational model where \(N\) agents were located on a small-world network (Watts & Strogatz 1998). When generating networks, we first considered an expanded cycle where agents were arranged in a circle and were connected with \(d / 2\) neighbours on both sides; then, we added \(Ndp / 2\) random links (Newman et al. 2000). Loops and duplicated links were avoided. Following this procedure, the average degree size, that is, the number of neighbours, was \(d (1 + p)\). A larger \(p\) indicated that the network had become more disordered. Previous studies have reported that disordered networks tend to induce consensus in different opinion formation models (see Flache & Macy 2011b and cited studies).

Each agent had an attribute called an opinion. The opinion of agent \(i\) was denoted as \(o_i \in \mathbb{R}\). Opinions could represent attitudes towards a specific policy. Positive and negative opinion values represented those for and against that policy; absolute opinion values indicated attitude strength. In the initial states, \(o_i\) followed a uniform distribution, \(\rm{U} (-3, 3)\). Note that the range of initial values does not indicate upper and lower bounds of opinions, and absolute values of agents’ opinions can be larger than 3. Agents could update their opinion through interactions with other agents. During each elementary time step, one agent could modify his/her opinion; in other words, we assumed asynchronous updating. During each step, an interaction with a neighbour occurred at a probability of \(1-w\), whereas interaction with mass media occurred at a probability of \(w\). Therefore, a larger \(w\) indicated a stronger influence of mass media.

Agents modified their opinion by interacting with their neighbours. During such an event, one focal agent, \(i\), was selected randomly from \(N\) agents; one role agent, \(j\), was also selected randomly from \(i\)’s neighbours. We assumed an assimilative interaction, and that \(i\)’s opinion was influenced by \(j\)’s opinion. Specifically, the opinion of the focal agent was updated in the following way:

In addition to assimilative interaction, random errors denoted by \(e\) also modified opinions. A random error term, \(e\), took the value \(\Delta\) or \(-\Delta\) with equal probability. This error term allowed for the possibility that the focal agent’s opinion diverged from the role agent’s opinion, which reflected the uncertain effects of persuasion. Although the original model (Laver 2020) assumed that assimilation occurred after adding an error term, we just added two components to permit a separate analysis of assimilation and errors.

In this model, mass media were external agents who influenced the opinions of other agents in networks, but did not modify their own opinions. We assumed that there were two mass media with competing opinions (Mckeown & Sheehy 2006; Bhat & Redner 2019). For instance, two mass media outlets may represent left- and right-wing opinions. Therefore, we assumed that the opinions of two mass media outlets were \(o_m\) and \(-o_m\), respectively. The fixed positions of mass media implied that mass media opinions changed much more slowly.

Agents in networks modify their opinions through interactions with mass media as well as with neighbours. During this event, one focal agent was selected similarly to when interactions with a neighbour occurred; then, mass media functioned as a role agent. The mass media agents followed were fixed during a simulation run. This setting meant that agents kept following left-oriented mass media (e.g. MSNBC) or right-oriented mass media (e.g. Fox News). At the beginning of a simulation run, each agent was assigned to either mass media outlet with equal probability. When interactions occurred, agents updated their opinion using the same method as during interactions with their neighbour. In other words, agent \(i\) updated his/her opinion in the following way:

Our main interest was the standard deviation of opinions that was denoted by \(\hat{\sigma}_o\). Smaller values suggested that people approached consensus states, whereas larger values suggested polarised opinions. In addition, we often referred to the standard deviation to assess accompanying uncertainty of this quantity. After a sufficiently long relaxation process that continued for from 160000\(N\) to 5500000\(N\) rounds, we recorded the quantity of interest for from 30000\(N\) to 420000\(N\) rounds. To enhance the statistical accuracy of the simulation results, we conducted at least ten simulation runs and reported the mean values of these outcomes.

Results and Discussion

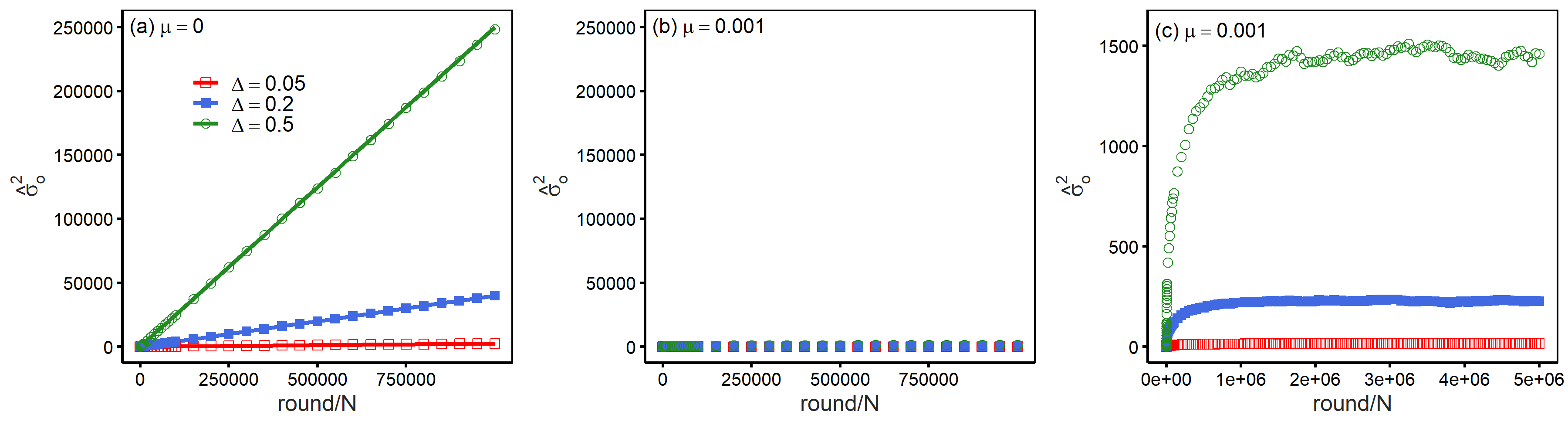
First, we checked the basic model characteristics when interactions with mass media were not considered. Figure 1 presents opinion variance (\(\hat{\sigma}_o^2\)) as a function of time. In this figure, we set the initial opinions of all the agents to 0 to clarify the time trend. Panel (a) presents the results when no social influence was involved with opinion formation (\(\mu = 0\)). Here, the model was reduced to a one-dimensional random walk whose movement unit size was \(\Delta\). The time evolution of the variance of simulated opinions could be approximated by a linear time trend. In contrast, we assumed weak assimilation (\(\mu = 0.001\)) in panel (b), and an unlimited increase in variance was prevented. Panel (c) reports the same result for a longer time period and indicates that opinion variance in fact reached stables values once assimilation was introduced (note that values of both axes are different in panel (c)). Therefore, we assumed (weak) assimilation below and investigated the stationary heterogeneity of simulated opinions.

To understand the model’s basic behaviour, Figure 2 reports the values of \(\hat{\sigma}_o\) as a function of a rewiring probability in generating small-world networks (\(p\)). Small increases in \(p\) significantly lower the values of \(\hat{\sigma}_o\). Although further increases in \(p\) lead to smaller \(\hat{\sigma}_o\), its marginal effects become smaller. Our result was consistent with previous studies that observed that disordered networks tend to move towards consensus (Flache & Macy 2011b). The effects of other parameters are intuitive; a stronger tendency towards assimilation (\(\mu\)) reduces opinion heterogeneity, whereas a larger error (\(\Delta\)) increases opinion heterogeneity.

Figure 3 reports the values of \(\hat{\sigma}_o\) as a function of \(d\) which controls the average degree of networks. The values of \(\hat{\sigma}_o\) decreased as \(d\) took larger values, which means that a larger degree size decreased opinion heterogeneity. At the same time, this figure also shows that adding connections to the nearest neighbours had smaller effects than adding random links by increasing \(p\). For example, panels show that an opinion approached consensus by increasing the values of \(d\) from 4 to 14 when \(p = 0\). Almost the same magnitude of heterogeneity reduction was achieved by increasing the value of \(p\) from 0 to 0.01, but this modification only increased the average degree from 4 to 4(1 + 0.01). Therefore, this figure suggests that disordered networks are efficient at achieving a less polarised opinion distribution.

From here, we introduced mass media and examined how they contribute to the resulting opinion distribution. Panels (a1)–(d1) of Figure 4 reports \(\hat{\sigma}_o\) as a function of \(w\). Introducing opportunities for interactions with mass media reduces opinion heterogeneity. The values of \(\hat{\sigma}_o\) decreased as \(w\) took larger values, and this pattern was more notable when assimilation was weak (small \(\mu\)) and networks were less disordered (small \(p\)). Where \(w\) was not overly large, the figure shows that the extremity of media (\(o_m\)) whose values range from zero to four had a small impact on the extent of heterogeneity reduction. However, further large \(w\) increased opinion heterogeneity whose extent depended on the value of \(o_m\).

Panels (a2)–(d2) report the standard deviations of \(\hat{\sigma}_o\) using the same parameter values to assess uncertainty. An increase in the frequencies of interaction with mass media reduced standard deviations, given that \(w\) remained small, which corresponded to a decrease in \(\hat{\sigma}_o\). However, a further increase in \(w\) did not lead to significant increases in standard deviations in contrast to the values of \(\hat{\sigma}_o\). Furthermore, the values of standard deviation decreased as \(w\) approached one.

Panels (a1)–(d1) of Figure 5 reports \(\hat{\sigma}_o\) as a function of \(o_m\) to further understand the role of mass media. The figure shows that \(o_m\) had a small impact on opinion heterogeneity as long as the value of \(w\) was sufficiently small as suggested in Figure 4. In contrast, \(\hat{\sigma}_o\) increased monotonically with the size of \(o_m\) when the probability of interaction with mass media was larger. Therefore, a large \(w\) led to less opinion heterogeneity when \(o_m\) was small, but an opposite pattern was observed with larger values of \(o_m\). The standard deviation shows similar patterns in panels (a2)–(d2). Its value increased with \(o_m\) when \(w\) was large. At the same time, comparing the cases of \(w = 0.1\) and \(w = 0.3\) reveals that the increase in standard deviation was modest; large differences were not observed in contrast to the values of \(\hat{\sigma}_o\).

Figure 6 presents opinion distributions to gain a clearer understanding of the effects of mass media. We conducted 500 simulation runs and recorded opinions at the \(500000N\)th round to report this result. Panel (a) presents the results with weak mass media influence. Opinion distributions shrank when a small probability of interacting with mass media was introduced (\(w = 10^{-3}\)). Mass media positions had a negligible impact on the distributions. In this figure, the largest value of \(o_m\) was eight. Although this value lies at almost the edge of opinion distributions when \(w = 0\), the introduction of mass media still decreased opinion heterogeneity. In contrast, panel (b) shows that opinion distributions polarised when the interaction with mass media was frequent (\(w = 0.5\)). At this stage, the mass media have an overly high influence, and their positions are reflected in opinion distributions. As the positions of mass media became more extreme, we observed the two peaks at more extreme positions.

These results suggest that the mass media play a different role depending on the values of \(w\). The mass media generated indirect connections because half of the agents were influenced by one media and that influence diffused through network interactions. Agents could moderate their opinion through interactions with neighbours who were influenced by different mass media. Mass media played a similar role to the additional links in networks (i.e. larger \(p\)) and reduced opinion heterogeneity. At this stage, mass media positions played a relatively minor role as suggested by the limited effects of \(o_m\) in Figures 4 and 5. In contrast, polarised mass media opinions exerted their influence once \(w\) became sufficiently large. At this stage, agents’ opinion formation was dominated by mass media opinions, and the polarisation of mass media contributed directly to opinion heterogeneity among agents. Furthermore, this polarised state corresponded to the fact that the standard deviation did not increase despite the increase in \(\hat{\sigma}_o\). The followers of each medium were concentrated around the positions of mass media, which led to relatively stable states.

Non-monotonic patterns can be observed with another system parameter. Panels (a1)–(d1) of Figure 7 present the effects of assimilation strength (\(\mu\)). As the values of \(\mu\) became larger, a decline in opinion heterogeneity was observed; stronger assimilation made opinion distributions approach consensus states. In contrast, further increases in \(\mu\) led to an increase in opinion heterogeneity. This reversal tends to be prominent when mass media positions became extreme, that is, larger \(o_m\). External agents with a fixed opinion attracted followers, which reversed the direction of the effects of the assimilation parameter. Again, this tendency did not necessarily contribute to a large standard deviation in \(\hat{\sigma}_o\), as indicated in panels (a2)–(d2). The study observed that the standard deviation did not increase with large frequencies of interaction with mass media (\(w = 0.3\)).

Figure 8 reports opinion heterogeneity as a function of \(w\) and \(\mu\) to fully understand the effects of these two parameters. Two parameters demonstrated a monotonic impact when the value of \(o_m\) was small. Panel (a) shows that \(\hat{\sigma}_o\) decreases as \(w\) and \(\mu\) increase, which indicates that both the frequency of interaction with mass media and intensity of assimilation contribute to reduced opinion heterogeneity.

In contrast, non-monotonic patterns appeared when \(o_m\) was large. Panel (b) shows that \(\hat{\sigma}_o\) had the smallest values with intermediate \(w\), and this non-monotonic relationship was prominent with smaller values of \(\mu\). When \(\mu\) was sufficiently large and \(\hat{\sigma}_o\) took very small values, higher frequencies of interaction with mass media monotonically increased opinion heterogeneity.

Finally, we examined how the introduction of mass media modified the dependence on other parameters. Figure 9 reports the values of \(\hat{\sigma}_o\) as a function of \(w\) for different values of \(p\). As reported in Figure 2, more disordered networks (larger \(p\)) reduced opinion heterogeneity without the influence of mass media. However, this effect diminished as \(w\) became larger, and the difference between the results with \(p = 0.001\) and \(p = 0.1\) almost disappeared when the value of \(w\) was approximately 0.1. This figure shows that interactions with mass media can dominate other parameters even when the majority of interactions occur between neighbours.

Conclusion

In sum, we extended and examined the noisy opinion formation model proposed in Laver (2020), where weak assimilation intensity and errors preserved opinion heterogeneity. Our model focused on the role of external agents with fixed opinions, that is, mass media. First, we examined the basic behaviour of the model in the absence of mass media. Opinion heterogeneity converged even with weak assimilation intensity. Additional links, especially long-range links, reduced opinion heterogeneity significantly. Next, we introduced mass media and examined their impact on opinion distributions. The frequency of interaction with mass media indicated non-monotonic effects on opinion heterogeneity. Small increases in interaction frequencies reduced opinion heterogeneity, and this pattern could be observed even with extreme mass media positions. The effects of mass media on opinion positions were negligible with a lower frequency of mass media interaction. At this stage, mass media played the same role as additional network links and contributed to the reduction of opinion heterogeneity. In contrast, more frequent interactions with mass media increased opinion heterogeneity. High frequencies of mass media interaction attracted agents’ opinions and contributed to polarisation. The assimilation intensity also demonstrated non-monotonic effects, and both weak and strong intensities contributed to opinion heterogeneity. Finally, higher frequencies of interaction with mass media dampened the effects of network-related parameters.

Our simulation results imply that multiple mass media with opposite positions can play qualitatively different roles. A moderate influence of mass media can reduce opinion heterogeneity by offering a shared basis for people’s opinions, although mass media do not occupy the centre of an opinion spectrum. Conversely, mass media can foster opinion heterogeneity when its influence becomes overly large. Empirical studies have found that mass media influence explains the recent rise of polarisation (Hopkins 2014; Martin & Yurukoglu 2017). Our simulation suggests that the mass media’s strong influence attracts followers to extreme positions.

Finally, our study had some limitations that have implications for possible future studies. We assumed a tendency towards assimilation including in interactions with mass media. However, some studies have also considered the possibility of repulsion in opinion formation, and this modification produces some novel system behaviour (Jager & Amblard 2005; Vaz Martins et al. 2010; Flache & Macy 2011b; Chen et al. 2017; Huet & Mathias 2018; Turner & Smaldino 2018). Although the empirical validity of opinion repulsion remains ambiguous according to recent experimental studies (Bail et al. 2018; Guess & Coppock 2020; Takács et al. 2016), we can examine whether the introduction of repulsion is useful when replicating stylised facts. In addition, network links were fixed in this simulation. Dynamic networks tend to produce opinion diversity (Centola et al. 2007; Kozma & Barrat 2008), but diversity can disappear if errors are introduced in the link updating process (Grauwin & Jensen 2012). Links with mass media were also fixed in this study, but these links may also be modified considering selective exposure (Iyengar & Hahn 2009; Stroud 2008). Although mass media had negligible effects on opinion heterogeneity when the interaction frequency was low, dynamic relationships with mass media may lead to different patterns. Although this study had these limitations, we believe the basic patterns reported here would be a good basis to investigate more complex situations.

References

AXELROD, R. (1997). The dissemination of culture: A model with local convergence and global polarization. Journal of Conflict Resolution, 41(2), 203–226. [doi:10.1177/0022002797041002001]

BAIL, C. A., Argyle, L. P., Brown, T. W., Bumpus, J. P., Chen, H., Fallin Hunzaker, M. B., Lee, J., Mann, M., Merhout, F., & Volfovsky, A. (2018). Exposure to opposing views on social media can increase political polarization. Proceedings of the National Academy of Sciences, 115(37), 9216–9221. [doi:10.1073/pnas.1804840115]

BAKSHY, E., Messing, S., & Adamic, L. A. (2015). Exposure to ideologically diverse news and opinion on Facebook. Science, 348(6239), 1130–1132. [doi:10.1126/science.aaa1160]

BANISCH, S., & Olbrich, E. (2019). Opinion polarization by learning from social feedback. Journal of Mathematical Sociology, 43(2), 76–103. [doi:10.1080/0022250x.2018.1517761]

BARBERÁ, P., Jost, J. T., Nagler, J., Tucker, J. A., & Bonneau, R. (2015). Tweeting from left to right: Is online political communication more than an echo chamber? Psychological Science, 26(10), 1531–1542.

BAUMANN, F., Lorenz-Spreen, P., Sokolov, I. M., & Starnini, M. (2020). Modeling echo chambers and polarization dynamics in social networks. Physical Review Letters, 124(4), 48301. [doi:10.1103/physrevlett.124.048301]

BHAT, D., & Redner, S. (2019). Nonuniversal opinion dynamics driven by opposing external influences. Physical Review E, 100(5), 050301. [doi:10.1103/physreve.100.050301]

CASTELLANO, C., Fortunato, S., & Loreto, V. (2009). Statistical physics of social dynamics. Reviews of Modern Physics, 81(2), 591–646. [doi:10.1103/revmodphys.81.591]

CENTOLA, D., González-Avella, J. C., Eguíluz, V. M., & San Miguel, M. (2007). Homophily, cultural drift, and the co-Evolution of cultural groups. Journal of Conflict Resolution, 51(6), 905–929. [doi:10.1177/0022002707307632]

CHEN, G., Cheng, H., Huang, C., Han, W., Dai, Q., Li, H., & Yang, J. (2017). Deffuant model on a ring with repelling mechanism and circular opinions. Physical Review E, 95(4), 042118. [doi:10.1103/physreve.95.042118]

CHRISTAKIS, N. A., & Fowler, J. H. (2009). Connected: The Surprising Power of Our Social Networks and How They Shape Our Lives. Little, Brown & Company.

COSENZA, M. G., Gavidia, M. E., & González-Avella, J. C. (2020). Against mass media trends: Minority growth in cultural globalization. PlOS ONE, 15(4), e0230923. [doi:10.1371/journal.pone.0230923]

DEFFUANT, G. (2006). Comparing extremism propagation patterns in continuous opinion models. Journal of Artificial Societies and Social Simulation, 9(3), 8: https://www.jasss.org/9/3/8.html.

DEFFUANT, G., Neau, D., Amblard, F., & Weisbuch, G. (2000). Mixing beliefs among interacting agents. Advances in Complex Systems, 3(01n04), 87–98. [doi:10.1142/s0219525900000078]

FLACHE, A., & Macy, M. W. (2011a). Local convergence and global diversity: From interpersonal to social influence. Journal of Conflict Resolution, 55(6), 970–995. [doi:10.1177/0022002711414371]

FLACHE, A., & Macy, M. W. (2011b). Small worlds and cultural polarization. The Journal of Mathematical Sociology, 35, 146–176. [doi:10.1080/0022250x.2010.532261]

FLACHE, A., Mäs, M., Feliciani, T., Chattoe-Brown, E., Deffuant, G., Huet, S., & Lorenz, J. (2017). Models of social influence: Towards the next frontiers. Journal of Artificial Societies and Social Simulation, 20(4), 2: https://www.jasss.org/20/4/2.html. [doi:10.18564/jasss.3521]

GALAM, S. (1997). Rational group decision making: A random field Ising model at T = 0. Physica A: Statistical Mechanics and Its Applications, 238(1–4), 66–80. [doi:10.1016/s0378-4371(96)00456-6]

GALAM, S., & Jacobs, F. (2007). The role of inflexible minorities in the breaking of democratic opinion dynamics. Physica A: Statistical Mechanics and Its Applications, 381(1–2), 366–376. [doi:10.1016/j.physa.2007.03.034]

GONZÁLEZ-AVELLA, J. C., Cosenza, M. G., Eguíluz, V. M., & San Miguel, M. (2010). Spontaneous ordering against an external field in non-equilibrium systems. New Journal of Physics, 12(1), 013010.

GONZÁLEZ-AVELLA, J. C., Cosenza, M. G., & Tucci, K. (2005). Nonequilibrium transition induced by mass media in a model for social influence. Physical Review E, 72(6), 065102.

GRAUWIN, S., & Jensen, P. (2012). Opinion group formation and dynamics: Structures that last from nonlasting entities. Physical Review E, 85(6), 066113. [doi:10.1103/physreve.85.066113]

GROEBER, P., Lorenz, J., & Schweitzer, F. (2014). Dissonance minimization as a microfoundation of social influence in models of opinion formation. The Journal of Mathematical Sociology, 38(3), 147–174. [doi:10.1080/0022250x.2012.724486]

GUESS, A., & Coppock, A. (2020). Does counter-attitudinal information cause backlash? Results from three large survey experiments. British Journal of Political Science, 50(4), 1497–1515. [doi:10.1017/s0007123418000327]

HEGSELMANN, R., & Krause, U. (2002). Opinion dynamics and bounded confidence. Journal of Artifical Societies and Social Simulation (JASSS), 5(3), 2; https://www.jasss.org/5/3/2.html.

HOPKINS, D. J. (2014). The consequences of broader media choice: Evidence from the expansion of Fox News. Quarterly Journal of Political Science, 9(1), 115–135. [doi:10.1561/100.00012099]

HUET, S. & Mathias, J.-D. (2018). Few Self-Involved Agents Among Bounded Confidence Agents Can Change Norms. Advances in Complex Systems, 21(06n07), 1850007. [doi:10.1142/s0219525918500078]

IYENGAR, S., & Hahn, K. S. (2009). Red media, blue media: Evidence of ideological selectivity in media use. Journal of Communication, 59(1), 19–39. [doi:10.1111/j.1460-2466.2008.01402.x]

JAGER, W., & Amblard, F. (2005). Uniformity, bipolarization and pluriformity captured as generic stylized behavior with an agent-based simulation model of attitude change. Computational & Mathematical Organization Theory, 10(4), 295–303. [doi:10.1007/s10588-005-6282-2]

JESSEE, S. A. (2009). Spatial voting in the 2004 presidential election. American Political Science Review, 103(1), 59–81. [doi:10.1017/s000305540909008x]

KLEMM, K., Eguíluz, V. M., Toral, R., & Miguel, M. S. (2003). Global culture: A noise-induced transition in finite systems. Physical Review E, 67(4), 045101. [doi:10.1103/physreve.67.045101]

KLOFSTAD, C. A., Sokhey, A. E., & Mcclurg, S. D. (2013). Disagreeing about disagreement: How conflict in social networks affects political behavior. American Journal of Political Science, 57(1), 120–134. [doi:10.1111/j.1540-5907.2012.00620.x]

KOZMA, B., & Barrat, A. (2008). Consensus formation on adaptive networks. Physical Review E, 77(1), 016102.

KURAHASHI-NAKAMURA, T., Mäs, M., & Lorenz, J. (2016). Robust clustering in generalized bounded confidence models. Journal of Artificial Societies and Social Simulation, 19(4), 7: https://www.jasss.org/19/4/7.html. [doi:10.18564/jasss.3220]

LAVER, M. (2020). Agent-Based models of polarization and ethnocentrism. Cambridge University Press.

LAZER, D., Rubineau, B., Chetkovich, C., Katz, N., & Neblo, M. (2010). The coevolution of networks and political attitudes. Political Communication, 27(3), 248–274. [doi:10.1080/10584609.2010.500187]

LELKES, Y. (2016). Mass polarization: Manifestations and measurements. Public Opinion Quarterly, 80(S1), 392–410. [doi:10.1093/poq/nfw005]

MACY, M., & Tsvetkova, M. (2015). The signal importance of noise. Sociological Methods & Research, 44(2), 306–328. [doi:10.1177/0049124113508093]

MARTIN, G. J., & Yurukoglu, A. (2017). Bias in cable news: Persuasion and polarization. American Economic Review, 107(9), 2565–2599. [doi:10.1257/aer.20160812]

MATHIAS, J.-D., Huet, S., & Deffuant, G. (2016). Bounded confidence model with fixed uncertainties and extremists: The opinions can keep fluctuating indefinitely. Journal of Artificial Societies and Social Simulation, 19(1), 6: https://www.jasss.org/19/1/6.html. [doi:10.18564/jasss.2967]

MÄS, M., Flache, A., & Helbing, D. (2010). Individualization as driving force of clustering phenomena in humans. PLoS Computational Biology, 6(10), e1000959.

MENG, X. F., van Gorder, R. A., & Porter, M. A. (2018). Opinion formation and distribution in a bounded-confidence model on various networks. Physical Review E, 97(2), 022312. [doi:10.1103/physreve.97.022312]

MUTZ, D. C. (2002). Cross-cutting social networks: Testing democratic theory in practice. American Political Science Review, 96(1), 111–126. [doi:10.1017/s0003055402004264]

NEWMAN, M. E. J., Moore, C., & Watts, D. J. (2000). Mean-field solution of the small-world network model. Physical Review Letters, 84(14), 3201–3204. [doi:10.1103/physrevlett.84.3201]

PERES, L. R., & Fontanari, J. F. (2010). The mass media destabilizes the cultural homogenous regime in Axelrod’s model. Journal of Physics A: Mathematical and Theoretical, 43(5), 055003. [doi:10.1088/1751-8113/43/5/055003]

PERES, L. R., & Fontanari, J. F. (2011). The media effect in Axelrod’s model explained. EPL (Europhysics Letters), 96(3), 38004. [doi:10.1209/0295-5075/96/38004]

PINEDA, M., & Buendía, G. M. (2015). Mass media and heterogeneous bounds of confidence in continuous opinion dynamics. Physica A: Statistical Mechanics and Its Applications, 420, 73–84. [doi:10.1016/j.physa.2014.10.089]

PINEDA, M., Toral, R., & Hernández-García, E. (2009). Noisy continuous-opinion dynamics. Journal of Statistical Mechanics: Theory and Experiment, 2009(8), P08001. [doi:10.1088/1742-5468/2009/08/p08001]

QUATTROCIOCCHI, W., Caldarelli, G., & Scala, A. (2014). Opinion dynamics on interacting networks: Media competition and social influence. Scientific Reports, 4, 4938. [doi:10.1038/srep04938]

SCHWEIGHOFER, S., Schweitzer, F., & Garcia, D. (2020). A weighted balance model of opinion hyperpolarization. Journal of Artificial Societies and Social Simulation, 23(3), 5: https://www.jasss.org/23/3/5.html. [doi:10.18564/jasss.4306]

SHIBANAI, Y., Yasuno, S., & Ishiguro, I. (2001). Effects of global information feedback on diversity: Extensions to Axelrod’s adaptive culture model. Journal of Conflict Resolution, 45(1), 80–96. [doi:10.1177/0022002701045001004]

STROUD, N. J. (2008). Media use and political predispositions: Revisiting the concept of selective exposure. Political Behavior, 30(3), 341–366. [doi:10.1007/s11109-007-9050-9]

TAKÁCS, K., Flache, A., & Mäs, M. (2016). Discrepancy and disliking do not induce negative opinion shifts. PlOS ONE, 11(6), e0157948.

TURNER, M. A., & Smaldino, P. E. (2018). Paths to polarization: How extreme views, miscommunication, and random chance drive opinion dynamics. Complexity, 2018, 2740959. [doi:10.1155/2018/2740959]

VAZ Martins, T., Pineda, M., & Toral, R. (2010). Mass media and repulsive interactions in continuous-opinion dynamics. EPL (Europhysics Letters), 91(4), 48003. [doi:10.1209/0295-5075/91/48003]

WANG, X., Sirianni, A. D., Tang, S., Zheng, Z., & Fu, F. (2020). Public discourse and social network echo chambers driven by socio-Cognitive biases. Physical Review X, 10(4), 041042. [doi:10.1103/physrevx.10.041042]

WATTS, D. J., & Strogatz, S. H. (1998). Collective dynamics of “small-world” networks. Nature, 393(6684), 440–442. [doi:10.1038/30918]