Modeling Interaction in Collaborative Groups: Affect Control Within Social Structure

,
and
University of Applied Sciences, Potsdam, Germany
Journal of Artificial
Societies and Social Simulation 24 (4) 6
<https://www.jasss.org/24/4/6.html>
DOI: 10.18564/jasss.4699
Received: 09-Dec-2020 Accepted: 12-Sep-2021 Published: 31-Oct-2021
Abstract
This paper studies the dynamics of identity and status management within groups in collaborative settings. We present an agent-based simulation model for group interaction rooted in social psychological theory. The model integrates affect control theory with networked interaction structures and sequential behavior protocols as they are often encountered in task groups. By expressing status hierarchy through network structure, we build a bridge between expectation states theory and affect control theory, and are able to reproduce central results from the expectation states research program in sociological social psychology. Furthermore, we demonstrate how the model can be applied to analyze specialized task groups or sub-cultural domains by combining it with empirical data sources. As an example, we simulate groups of open-source software developers and analyze how cultural expectations influence the occupancy of high status positions in these groups.Introduction
The study of groups is one place where the fields of psychology and sociology most apparently intersect, as individual-level information processing interacts with the dynamics of a social system. In this work, we follow the common definition of a group referring to "a bounded collection of interacting individuals" exhibiting functional, cognitive (we would add, affective), and structural interdependencies (Lindenberg 1997, 2015). While in the middle of the twentieth century small-group research was an integrated research field, it subsequently fragmented into multiple specialized domains such as the study of networks, social exchange, group collaboration, collective decision making, and many others (Burke 2006). These subfields differ in the degree to which they focus on one or more of these interdependencies.
However, some research questions are best tackled by an integrated approach that examines how these interdependencies are intertwined. In this vein, the present work sets out to understand how role identities and their culturally shaped affective connotations influence the cultural acceptance of those who occupy important positions in task groups. To this end, we built an integrative computational model called ACTING (Affect Control Theory based simulations of Interaction in Networked Groups) that can realistically simulate task group interactions. ACTING takes into account all three of the aforementioned group interdependencies because each influences task groups. Task groups are goal-oriented and often follow protocols or procedural rules to reach a shared goal (functional interdependence). They rely on shared group identities and a shared understanding of appropriate role-based identities and behaviors (cognitive-affective interdependence). Finally, workplace interactions in a task group often occur against the backdrop of explicit organizational hierarchies that determine who gets to interact with whom (structural interdependence).
In the last two decades, agent-based modeling (ABM) has been developed as a fruitful knowledge-integrating approach to sociological theory building and testing, in particular for understanding how macroscopic social effects arise from simple mechanisms operating at the individual level. ABM, therefore, naturally lends itself as a methodological framework to study emergent properties of groups, such as the emergence of cultural acceptance or rejection of status hierarchies in task groups. ABMs of group dynamics, particularly from computational organizational theories (Cohen et al. 1972; Decker 1996; Prietula & Carley 1994), have modeled functional, cognitive-affective, and structural interdependencies predominantly from an information processing perspective. Although these theories have increasingly emphasized the importance of cultural knowledge and normative expectations (Carley & Hill 2001), the encoding of this knowledge and expectations has primarily been either as agent rules dependent largely on the researcher’s knowledge and specific to a particular task domain, or as simulated knowledge of what and whom each agent knows. Consequently, with the present work we are addressing a gap in the organizational modeling literature, namely finding a tractable yet principled approach for modeling cultural dynamics. We are also addressing a gap in the group processes literature, namely incorporating identity maintenance processes into formal models of task groups. Existing models have either simulated agent’s role-identities (Heise 2013) but ignored the network structures and associated status hierarchies they operate in; or they have focused on the formation of status hierarchies and the associated network structures (Mark et al. 2009), but have ignored role identities entirely or focused on broad categories such as female versus male workers which are modeled as categorical variables.
Building on Heise’s (2013) work, we propose a more general framework for modeling task groups where cultural knowledge is encoded as sentiments collected from empirical surveys. Agents in our model orient themselves with respect to the sentiments they have about concepts and behaviors, forming expectations about who should do what with whom as they engage in networked and interdependent activities. While the functional interdependence of task groups will often be highly task-specific, we believe that a generalized model that captures the interplay of functional, cognitive-affective and structural interdependence is feasible. The social psychological concept of identity is key to this endeavor. On the one hand, identities are focal concepts organizing an individual’s goals, values, and relationships across different domains of daily life; on the other hand, identities are tied to structural positions in organizations and society.
In this work, we thus extend Heise’s (2013) Group Simulator, which employs a model of identity based on affect control theory, into a more general agent based model that can simulate complex task groups. The extensions include three major contributions. First, we allow for the simulation of interactions within networked group structures. In particular, this enables us to model and investigate the alignment of a group’s role identities with its organizational structure which is implemented as a directed graph \(G=(V,E)\) , where the vertices \(V\) are a set of agents and the edges \(E\) are a set of directed behavior pathways. This extension is important because the ability to manage expectations is heavily influenced by the group’s organizational structure. Furthermore, networks can be connected to status hierarchies that are present in the group, allowing us to investigate the functioning of role hierarchies within a variety of formal group structures. Note that this work grew out of an effort to model digital task-groups that collaborate online. In these settings, we repeatedly encountered interaction structures that were restricted to specific network topologies (Zöller et al. 2020). Moreover, we found that the possible actions of group members were often restricted to a discrete set of behaviors, owing to the technical design of the platform on which the interactions took place. Therefore, we introduced our second innovation to Heise’s (2013) model, the possibility to restrict the action space to a discrete set of behaviors. This feature is also helpful when one wants to compare simulation results to empirical data for which a discrete annotation scheme was employed such as Bales’s (1950) interaction process analysis categories. Finally, task group behavior often follows a protocol. By protocol, we mean a task structure where the completion of certain tasks requires sequential actions from group members with different skillsets at different levels of authority. This is the case not only in computer-mediated collaboration on platforms, but also in bureaucratic organizations that enforce legal or other formal prescriptions of business processes. Consequently, certain actions necessarily follow others or are only possible as a response to other actions. Thus, we added a third extension that allows the user to define behavior protocols in our model, which govern sequences of actions in the simulated groups.
The article is organized as follows. First, we describe the theoretical basis, starting with a brief outline of relevant work about the interplay between social networks and role behavior in task groups followed by a review of Affect Control Theory. Next, we describe our ACTING model, following the established ODD protocol for ABM description (Grimm et al. 2020). We then turn to a series of simulation experiments aimed at understanding the network functionality of the model in the context of several stylized ideal types of network structures. We investigate how different network structures influence the affective dynamics of identity management of interdependent group members. Furthermore, we demonstrate how the model reproduces well-known empirical findings about cultural expectations and status dynamics in small groups (Ridgeway 2019; Ridgeway & Bourg 2004). We then demonstrate how our framework can be used to model complex task groups that exhibit functional, cognitive-affective, and structural interdependencies, or what Merton (1957) called role-sets, i.e "the complement of role-relationships in which persons are involved by virtue of occupying a particular social status". The last methodological step is an application of the model to different empirically realistic interaction structures extracted from the GitHub social graph, to show how simulations help illuminate the identity dynamics and associated status positions that occur in various types of organized collaboration.
Background
Sociality and cognition are inextricably linked (Donald 1991; Dunbar 2009). Groups provide arenas for social learning and skills transmission (Hobaiter et al. 2014). Learning to join and work in groups is critical for children to develop a theory of mind and a sense of agency (Corsaro & Molinari 2005; Piaget 1977). The social networks of social animals (the patterns of relations between group members) influence behaviors related to reproduction, cooperation, conflict, and tool use (Connor et al. 2001; Hobaiter et al. 2014; Kappeler 1999). In humans, they influence patterns of reciprocation (Cook & Emerson 1978), perceptions of risk (Molm et al. 1999), and group solidarity (Markovsky & Lawler 1994). Finally, groups are where dominance relations are sustained and reproduced (Fararo & Skvoretz 1986; Mark et al. 2009; Skvoretz et al. 1996).
Status dynamics in task groups
Because task groups are important in the allocation of social goods (Berger et al. 1972; Bales & Slater 1955), they have long been the focus of scholars interested in the reproduction of status inequality. By status, we mean both ascribed (e.g., gender and race) and achieved (e.g., a post-secondary degree) characteristics that confer prestige across multiple group settings. Merton (1957, p. 110) observed that status and roles serve to connect culturally defined expectations with the patterned conduct and relationships that make up a social structure. He focused on the reproduction of status in work settings through the enactment of role sets. Role sets describe role identities such as doctors, nurses and interns that not only imply a set of attributes such as good or potent but also a set of logical relations such as directing and reporting.
Bales and colleagues (Bales 1953; Bales & Strodtbeck 1951) found that groups whose members were presumably initially equal in status, nevertheless exhibited inequalities in participation and influence. This empirical puzzle was the launching point for the expectation states research program in social psychology (Berger et al. 1972; Ridgeway 1991, 2019). The expectation states literature includes a variety of theories; but, central to them all is the notion that goal oriented groups when they form confront an information problem - they do not know who is competent. Group members, thus, must infer competence from social cues such as wealth and prestige. If a correlation exists between resources and nominal characteristics such as race or gender in the population, even if this correlation is spurious, a self-reinforcing pattern of interaction can arise that associates competence with the given characteristic (Ridgeway 1991). These differential expectations create a self-fulfilling prophecy (Merton 1968) whereby higher-status group members are more influential and receive disproportionately more positive evaluations and rewards.
Demonstrating how such an endogenous mechanism might operate and testing theoretical assumptions regarding this process has included pioneering simulation studies examining the formation of dominance hierarchies (Grow & Flache 2019; Skvoretz et al. 1996), the exercise of weak power through social exclusion (Markovsky et al. 1993), the attribution of status value to nominal characteristics (Lynn et al. 2009; Mark et al. 2009), and the formation of trust and cooperation (Flache & Macy 2011). In all of these simulation studies, status hierarchies have been defined and quantified through network properties. For example, Skvoretz et al. (1996) identify dominance hierarchies by analyzing the directionality of ties. Similarly, Lynn et al. (2009) use in-degree centrality of a deference network as the metric for status ranking. Centrality measures have a long-standing tradition as useful metrics in sociological theory building (Friedkin 1991). Examples are Hubbell’s measure of sociometric status (Hubbell 1965), Coleman’s measure of power (Coleman 1973), and Burt’s measure of prestige (Burt 1982). Freeman (1978) identified three different families of centrality that imply three competing theories of how centrality might affect group processes. It is, therefore, important to note that while in most cases a useful metric of group status can be defined in terms of network properties, the exact form will always depend on the specific context and the meaning of ties and nodes in the network. A general review about network theory and small groups can be found in Katz et al. (2004).
In the simulation studies conducted as part of the expectation states program cited above, status characteristics such as gender are typically operationalized as categorical variables that influence an individual’s opportunities to participate in group activities. Role identities such as CEO, supervisor, secretary or intern are not taken into account. However, by jettisoning role identities, an important factor in the relationship between perceived competence and status characteristics is lost. For example, gender scholars (Connor & Fiske 2018; Fiske & Stevens 1993; Moss-Racusin et al. 2010; Rudman 1998) have found that female leaders experience more scrutiny because gender expectations and role expectations are misaligned (the warmth versus competence dilemma). Thus, they are at greater risk of being unable to leverage their present status in future group interactions (Ridgeway & Smith-Lovin 1999).
In our present study, the focus is on how role expectations that are encoded in affective identities integrate with explicit organizational hierarchies to influence the impressions group members have about one another. Specifically, our focus is to distinguish between group settings where agents are likely to be able to manage expectations given their role, traits, and structural position from settings where this is less likely. By examining the interaction of these factors, we are able to re-integrate role performance as a determinant of status within a generative model using a parsimonious but flexible representation of task groups. To generate the role expectations, we define task groups as role systems where each agent is assigned an identity. We assume that group members seek to fulfill their role identities and behave accordingly, where role identity can be understood as "internalized social positions and their meanings" (Owens et al. 2010). Because behaviors are often definitional to role identities (e.g., teaching and teachers, sentencing and judges, programming and software developers, etc.), we compare situations where agents are able to draw on a wide array of behaviors to affirm their roles, and situations where behaviors are circumscribed by the task or institutional domain. Essentially, we assume that group members orient themselves with respect to affective meanings during group interactions. To develop this claim, we briefly describe affect control theory as it applies to group interaction.
Affect Control Theory
Affect Control Theory (ACT) is a quantification of classic symbolic interactionist and cultural constructionist ideas about social interaction as based on linguistic meanings of social objects. The theory conceptualizes culture as a collectively shared representation of identities, social behaviors, and modifiers such as personality traits and emotional states (Heise 2007). These concepts are assumed to populate a three-dimensional affective space that spans the three base dimensions of evaluation (how good vs. bad is the person, behavior, or modifier?), potency (how powerful vs. weak is it?), and activity (how active and noisy vs. passive and quiet?). These dimensions, collectively referred to as EPA, have been shown in decades of research to structure the semantic relations of social concepts in psycholinguistic rating studies, and are hypothesized to reflect cross-cultural universals of socio-emotional behavior and experience (Osgood et al. 1975). The empirical basis of ACT accordingly consists of databases of fundamental affective meanings (denoted \(F\) in subsequent equations) of usually many hundred to a few thousand social concepts, assessed in population surveys which tend to show considerable consensus about these meanings within linguistic communities (Ambrasat et al. 2014).
Descriptions of social reality require conceptual combinations. E.g., we expect a "cynical manager" or a "lazy worker" to act differently than a "manager" or a "worker" as such, respectively. These so-called affective amalgamations can be modeled with weighted regression equations that take the fundamental affective meanings of the constituent concepts as input and return an experientially quite accurate EPA vector as output (Averett & Heise 1987). The regression weights come from vignette experiments where participants provide EPA ratings of conceptual combinations. Similarly, ACT scholars have modeled the impressions resulting from specific behaviors such as "a manager scolding a worker" or "a worker ignoring a manager". Again, vignette experiments provide the empirical basis for parameterizing regression equations that take EPA vectors for actor, behavior, and object as input and return a vector for the transient impressions (denoted \(\tau\) in subsequent equations) resulting from the described social event as output (Gollob 1974).
In a given culture, role identities entail normative expectations of behavior. E.g., we would expect a manager to train, supervise, or interview a worker but find it inappropriate if they demeaned, ridiculed, or discouraged them. Mathematically, such expectations are modeled as deflection \(d = (F-\tau)^2\), an inverse measure of the degree to which transient impressions from a social event confirm the fundamental affective meanings of the involved role identities (Heise 2007; Morgan et al. 2016). ACT is a control theory precisely because it assumes that people are motivated to keep deflection to a minimum; hence, intuitively aligning their social actions with the normative order of their culture. This fundamental principle is in line with a large body of work in social psychology and cognitive science emphasizing the need to maximize cognitive and emotional coherence of thought and action (Hoey et al. 2021; Powers 1973; Thagard 2001). Much empirical work in the ACT research tradition has shown that the deflection-minimization principle predicts the perceived likelihood of verbally described social events, actual verbal and nonverbal behavior in experiments, and even EEG parameters related to expectation violation (e.g., Schauenburg et al. 2019; Schröder & Scholl 2009).
Because of ACT’s unique capacity to quantify the symbolic content of social cognitions and their behavioral consequences, the theory lends itself as a conceptual and empirical basis for social simulation. INTERACT (Heise 2007, p. 139) is a legacy program written in Java that allows one to model sequences of a dyadic interaction. A more recent probabilistic implementation of ACT as a partially observable Markov decision process called BayesACT (written in Python) has been used to simulate the effects of uncertainty and multiple role identities on the emergence of social structure(Schröder et al. 2016). Most relevant for the present article is Group Simulator, an agent-based model of small-group dynamics written in Netlogo, whose individual agents act according to the affect-control principle of minimizing deflection (Heise 2013). Heise’s simulation results yielded remarkable agreement with empirical behavior distributions of jury deliberations from classical empirical studies of group dynamics. In the present paper, we build on the Group Simulator to study the alignment of network structures and role identities in work groups.
ACTING Model
We name the agent-based model presented here ACTING (Affect Control Theory based simulations of Interaction in Networked Groups). The model was implemented in Python using the mesa library for ABM (Masad & Kazil 2015), and the source code for the model and Jupyter notebooks with all simulations presented in this article can be found at https://github.com/nikozoe/ACTING. Here, we present a shortened version of the model description following the ODD (Overview, Design concepts, Details) protocol (Grimm et al. 2020). The complete, detailed version, including all design principles and submodel descriptions is provided in the appendix.
The overall purpose of our model is to simulate task group interactions in order to understand and analyze the interplay between role identities, role expectations, status hierarchies, and the group’s interaction structure. Specifically, we are addressing the following question: Based on their role identities, which team members are more or less likely to occupy high status positions? The formalization of how the effort to maintain role identities translates into role expectations and behaviors is guided by affect control theory (ACT). Thus, another purpose of the model is to bridge the sociological theories of ACT and status characteristics. To consider our model realistic enough for its purpose, we use patterns in behavior distributions and formation of status hierarchies.
The model is grounded in empirical data and it is adaptable to task groups that operate in specific subcultures. For this purpose, a small survey has to be conducted to obtain ratings of central role identities and behaviors. We demonstrate this process by modeling teams of open source software developers, where the interaction structures are derived from empirical observations (Zöller et al. 2020).
Entities, state variables, and scales
The model includes the following entities: agents which represent members of a task group, a group object (optional) which represents the group identity, and the global environment which is either provided by the GroupModel or by the ProtocolGroupModel. An overview about all entities and their state variables can be found in Table 1.
| Variable name | Variable type | Meaning |
|---|---|---|
| GroupMember | ||
| F | \([\)real, real, real\(]\), static | Fundamental identity consisting of three values in the dimensions Evaluation, Potency, Activity (EPA) |
| T | \([\)real, real, real\(]\), dynamic | Transient identity consisting of three values in the EPA dimensions |
| acting | boolean, dynamic | True if the agent is acting at the current time step |
| Group | ||
| F | \([\)real, real, real\(]\), static | Fundamental identity consisting of three values in the EPA dimensions |
| T | \([\)real, real, real\(]\), dynamic | Transient identity consisting of three values in the EPA dimensions |
| GroupModel | ||
| schedule | object, dynamic | Keeps track of the current time step, also keeps track of the agents whose order is shuffled randomly at each step. |
| actor | GroupMember, dynamic | Reference to group member who gets to act at current time step |
| object | GroupMember or Group, dynamic | Reference to group member who is acted upon at current time step |
| action | [real,real,real], dynamic | Behavior at current time step consisting of three values in the EPA dimensions |
| datacollector | object, dynamic | collects agent and model data for later retrieval |
| ProtocolGroupModel If the task group is following a protocol, ProtocolGroupModel is instantiated instead of GroupModel from which it inherits. That means all state variables listed under Group Model are also state variables of ProtocolGroupModel. |
||
| n_iterations | int, dynamic | Specifies the length in time steps of the current protocol part. |
| select_actor | string, dynamic | Optional, is interpreted as python code and overwrites the select_actor method from the GroupModel |
| code | (string,string), dynamic | Optional, is interpreted as python code. code[0] is executed before the current protocol part; code[1] is executed after the current protocol part. |
| Parameters of GroupModel that become state variables of ProtocolGroupModel | ||
| reciprocity_rate | float, static | Probabilty for an action to be reciprocal |
| object_choice | string, static | Mechanism by which the object (agent who is acted upon) is chosen. Options are min event-tension,max deflection-reduction or random. |
| action_on_group | Boolean, static | Sets whether actions on the whole group are possible. |
| group_action_rate | float, static | Sets the propability for an action to be on the whole group. Only makes sense if action_on_group is True. |
| network_structure | Matrix with entries 1 and 0, static | Adjacency matrix of a network graph that determines who can act on whom |
| discrete_actions | list of floats, dynamic | List of possible actions. Each action is parsed as a list of EPA values. |
Group members: All agents in the model are initialized with a fundamental identity \(F\), which remains constant during a simulation run, and an event-driven transient identity, \(\tau\), which changes through interactions with other agents in the group. Both consist of 3-dimensional arrays \([E, P, A]\) with values for evaluation, potency and activity. An agent’s deflection \(d = (F-\tau)^2\) represents the affective dissonance an agent experiences between their situational and their fundamental identity.
Group object: Lawler et al. (2000) find that emotions produced through the interactions of group members are attributed in part to relevant social units. The group identity consequently forms over time through repeated and consistent interactions between its members. Depending on which kind of a group situation one wants to model, it may or may not be sensible to include a group object. Therefore, our implementation of the model makes the integration of a group object optional. In some of the simulations presented in this paper, it is included while in others it is not, depending on the group setting and the focus of the research question. When included, it is simulated as a pseudo agent that like the group members holds a fundamental and a transient identity. The group object can be acted upon, but can not act itself.
Global environment: In our implementation, the global environment inherits from the Model class of the Python package mesa (Masad & Kazil 2015). It is either constituted by the GroupModel or its extension ProtocolGroupModel. GroupModel keeps track of the current time step, the order of agents at each time step, who is acting on whom and also the data collection. Parameter settings of the global environment regulate which actions are available (discrete_actions), how often actions are reciprocal (reciprocity_rate), how often an action is performed on the group object (action_on_group) and who can act on whom (network_structure). If the simulated task is made up of a predescribed sequence of actions, the global environment is best represented by the ProtocolGroupModel. ProtocolGroupModel lets the researcher define a protocol in which the global environment changes over time including all aforementioned parameters. Most importantly, this allows the researcher to define different sections of the protocol of different length (n_iterations) for which only a discrete set of actions is available (discrete_actions) to the group members. Further customizations options (select_actor, code) make the ProtocolGroupModel very general and expressive, so that it can be adapted to specific work flows of specialized task groups.
As for the spatial and temporal resolution and extent of the model: Each time step corresponds to an action that is performed by one of the group members. The model does not represent physical space, but instead it represents EPA space in which fundamental and transient identities of agents are located as well as behaviors.
Process overview and scheduling
The most important process, which is repeated every time step, is an action being performed by one agent (actor) on another agent (object). First the actor is determined. This is generally the group member with the highest deflection unless the action is probablistically determined to be reciprocal. Next, the object and behavior are determined according to the chosen object selection criterion and ACT principles (see Equation 5). Finally, the action is performed, the resulting changes to the transient identities of all involved agents are applied and the resulting deflection is calculated. There is a chance that the action is directed towards the whole group determined by the model parameter group_action_rate. In this case, all group members except the actor experience the action as if they had been the object.
Design concepts
The most important design concepts of the model are basic principles, objectives and interaction which we present here in some detail. For additional design concepts, see the Appendix.
Basic principles
The model, modifying and extending Heise’s (2013) Group Simulator, conceptualizes a small group as a "team" in which individuals are committed to helping each other maintain their identities. The formalization of how this effort to maintain role identities translates in role expectations and behaviors is guided by Affect Control Theory, a mathematically specified theory of symbolic interaction (Heise 2007).
An event in ACT consists of an actor A that directs a behavior B towards an object O. After an event, the transient impressions of the actor, object and behavior are changed according to empirically parameterized impression formation equations:
| \[\begin{aligned} \boldsymbol{\tau}^T =& \;( A_e \quad A_p \quad A_a \quad B_e \quad B_p \quad B_a \quad O_e \quad O_p \quad O_a ) \end{aligned}\] | \[(1)\] |
| \[\begin{aligned} \mathbf{t}^T =& \; (\; 1 \quad A_e \quad A_p \quad A_a \; ... \; B_e \; ... \; O_e \; ... \; A_eB_e \; ... \; A_eO_e \; ... \; B_eO_e \; ... \; \\ A_eB_eO_e \; ... \; A_aB_aO_a \; ) \end{aligned}\] | \[(2)\] |
| \[\begin{aligned} \boldsymbol{\tau}_{aft} = & \;\mathbf{M} \; \mathbf{t} \end{aligned}\] | \[(3)\] |
Objectives
The agents’ objective is to choose the action that will most confirm their own fundamental identity and the fundamental identities of others. In this regard, the model follows the ACT principle stating that people seek to verify cultural knowledge about the social order (Heise 2007). Formally, this means that agents choose their behavior in order to minimize event deflection \(D\) which is defined as
| \[D = (F - \boldsymbol{\tau}_{aft})^2, \quad F^T = \; ( \overline{A}_e \quad \overline{A}_p \quad \overline{A}_a \quad \overline{B}_e \quad \overline{B}_p \quad \overline{B}_a \quad \overline{O}_e \quad \overline{O}_p \quad \overline{O}_a )\] | \[(4)\] |
| \[\dfrac{\partial D}{\partial B_i} = \dfrac{\partial(F - \;\mathbf{M} \; \mathbf{t})^2}{\partial B_i} \overset{!}{=} 0 \;, \quad i = e,p,a \] | \[(5)\] |
For the full mathematical form of B and its detailed derivation, see part II Mathematics of Affect Control Control theory in Heise’s book Expressive Order (Heise 2007).
Interaction
Actor and object selection: In each step of a simulation run, only one actor gets to act on one object which is either another agent or, if applicable, the group object. When an actor and an object are determined and their fundamental and transient identities are known, ACT provides a framework to calculate the optimal behavior which follows cultural norms, preserves role identities, and minimizes affective dissonance to the greatest possible extent (see Objectives). However, ACT provides no clear guidance on how to select an actor or an object in a group setting. This is not surprising since the ACT equations are derived from dyadic vignette experiments. Realistically, who acts upon whom in task groups is often task specific. Nonetheless, we assume that affective reasoning influences actor and object selection because it has an effect on the amount of affective dissonance experienced within the group which agents seek to minimize as per affect control theory’s control principle.
In our model, we follow Heise (2013) and assume that the agent who experiences the most deflection will be the next to act. This means that affective dissonance is the only driving force in turn-taking, which in the absence of task-specific information seems sensible. There are other options available in the model implementation like for example random actor selection that might be more accurate depending on the group and the task one wants to model.
After an actor is determined, the object selection criterion regulates how the object that the actor will act upon is chosen. One possible criterion is minimum event tension which was also used in Heise’s (2013) study to model juries. The minimum event tension criterion works as follows: once the actor is set, for each object candidate the optimal behavior is determined according to ACT. Subsequently, the action is carried out hypothetically and the resulting after-event deflection is calculated, which involves only the fundamentals and the transients after the event for the actor, object and behavior. Finally, the actual object is chosen so that this after-event deflection is minimized.
The minimum event tension criterion has the short-coming that it only considers the situational deflection of the actor, object and behavior triple after the event. However, Heise points out himself in the article (Heise 2013) introducing his original model that it aims at integrating Goffman’s (1959) suggestion that "a small group operates as a team in which individuals are committed to helping each other maintain their identities (faces)". Furthermore, Heise claims that "an individual motivated to action selects as object the group member who provides an optimal basis for creating a tension-reducing action that will confirm the fundamental affective meanings of actor and object". However, this tension reduction is not properly taken into account by the minimum event tension criterion. We therefore introduce a different object selection criterion that, in our opinion, adheres even more closely to the control principle. We term the criterion maximum deflection reduction, because it tries to reduce overall affective deflection instead of only causing a minimally deflective event. It works as follows: once the actor is set, for each object candidate the optimal behavior is determined based on ACT’s impression change equations and subsequently the hypothetical after-event deflection is calculated. But this is now compared to the overall deflection before the event from which the after after-event deflection is subtracted. Object and behavior are then chosen such as to maximize this difference, i.e. the deflection reduction. This means that both the transient identities and the overall deflection before and after the event are taken into account.
Action space: Past ACT models have assumed a continuous connotative action space along the dimensions evaluation, potency and activity, where each point can be mapped to a denotative label, i.e. the name of a behavior in natural language. In our model, the user can specify either a continuous action space, or define a discrete and finite set of possible actions. A discrete action space can be helpful in at least three ways. First, empirical data is often annotated using categorical taxonomies to describe the observed actions (Bales 1950). Although other behaviors might be possible, it is sensible to restrict simulation behaviors to the empirical annotation scheme in order to increase comparability. Second, there is a binning problem when mapping back in hindsight from connotative space to a categorical behavior set in denotative space because the volume that is mapped to each behavior might vary. This in return can lead to biased behavior distributions. Third, in many situations, agents simply only have a limited set of actions at their disposal. This might be due to institutional procedures or limited capabilities that are not captured by role identities. An obvious example where this is the case is the digital sphere. Behaviors might simply be restricted by a graphical user interface or a limited set of possible actions in an application. In our implementation, the action space is limited through passing a list of allowed behaviors in the environment parameter discrete_actions.
Interaction structure: In the model, the default setting is that every agent can act on every other agent. But, in many real world situations, who can interact with whom is governed by institutional hierarchies or organizational procedures. Therefore, the user can impose restrictions on who can interact with whom through passing the model a network structure in the form of an adjacency matrix. This means that an agent can only act on another agent if there exists a directed edge from the former to the latter in the network.
Protocols: Many task groups are structured by sequential protocols in which some actions necessarily have to follow others in order to complete a task. To allow for a realistic simulation of these groups, we include the possibility to parse such a protocol to the model in the form of a list in which each item represents one part of the protocol. What behaviors are available and how many actions should be carried out is specified for each step. Optionally, different settings for model parameters can be parsed before the beginning of each part as well as custom python code that should be executed before or after the protocol step. This flexibility makes the model expressive and allows one to customize the simulations to specific tasks and work flows of interest.
Simulations
We describe here a series of simulation experiments conducted with the ACTING model. First, we replicate Heise’s (2013) study simulating juries, which provides a baseline validation of our modified Group Simulator model and allows us to appraise the effects of the added features on model behavior. Second, we systematically explore the impact of different network topologies on affective dynamics of small groups according to the model, demonstrating how the model can be used to study how structural and cognitive-affective interdependencies interact in small groups. Third, we show how the model systematically reproduces empirical findings about status dynamics in groups following the expectation states research program in social psychology reviewed above. Lastly, we use the model to analyze interactions in teams of software developers on GitHub, based on a recent empirical study (Zöller et al. 2020), with the intention to show the practical usefulness and domain-specific adaptability of the model.
Application: Jury deliberations
The purpose of this section is two-fold. On the one hand, we reproduce Heise’s (2013) legacy study in which he simulated jury deliberations and compared the results to empirical data reported by Strodtbeck & Mann (1956). This serves as a sanity check for the basis of our model implementation. On the other hand, while reproducing these simulations, we explore two of the new features, examining how including these features influences Heise’s original model. First, we explore how including a discrete action space that restricts the behaviors available to the agents influences the model. Second, we explore how a new object selection criterion that aims at maximum deflection reduction instead of only minimizing after-event deflection influences agent behavior.
The empirical data set consists of annotated interpersonal actions in 29 jury deliberations as reported by Strodtbeck & Mann (1956). The actions were annotated in terms of Bales’s (1950) 12 Interaction Process Analysis (IPA) categories which are shown in Table 2. The reported EPA values are taken from Heise’s (2013) study and are based on a 1978 survey of North Carolina undergraduates (Smith-Lovin & Heise 2006).
| No | IPA Category Name | Concepts | E | P | A |
|---|---|---|---|---|---|
| 1 | Shows solidarity | help, compliment, gratify | 1.78 | 1.29 | .21 |
| 2 | Shows tension release | josh, laugh with, cheer | 1.48 | .91 | 1.12 |
| 3 | Agrees | agree with, understand, accommodate | 1.60 | .78 | .01 |
| 4 | Gives suggestion | encourage, cue, coach | 1.28 | 1.18 | .25 |
| 5 | Gives opinion | evaluate, analyze, entreat | 0.88 | 1.48 | 0.46 |
| 6 | Gives orientation | inform, educate, explain | 1.68 | 1.62 | 0.14 |
| 7 | Asks for orientation | quiz, question, ask about | 0.50 | 0.62 | 0.45 |
| 8 | Asks for opinion | consult, prompt, query | 0.48 | 0.74 | 0.16 |
| 9 | Asks for suggestion | entreat, ask, beseech | 0.30 | 0.24 | 0.09 |
| 10 | Disagrees | disagree with, ignore, hinder | 1.00 | 0.35 | 0.45 |
| 11 | Shows tension | fear, cajole, evade | -0.89 | -0.16 | 0.35 |
| 12 | Shows antagonism | argue with, deride, defy | -0.82 | 0.71 | 1.32 |
We conducted all simulations with the exact parameters used by Heise’s (2013). For convenience, we briefly state the model parameters here. All simulations modeled groups of 12 agents, 8 holding the fundamental identity of male juror \(\tilde{F} = [0.8, 1.6, -0.5]\) and 4 the fundamental identity of a female juror \(\tilde{F} = [1.2, 0.7, 0.0]\). The individual EPA values were based on the same 1978 survey as the IPA categories (Smith-Lovin & Heise 2006) and the conjoint identities of male and female juror were obtained with amalgamation equations (Averett & Heise 1987), which model how EPA connotations combine in conceptual combinations of nouns (here: juror) and adjectives (here: female). A group object initiated with the average fundamental and transient identities of all group members was included. Parameters for individuality and initial tension were set to 1.0, the action-on-group rate was set to 0.4 and the reciprocity rate was set to 0.8. For the rationale of these parameter settings, please refer to Heise (2013). All results shown here were averaged over 500 simulations, which ran for 1000 steps each.
We simulate six different settings that we evaluate subsequently against the empirical data. Three object selection criteria, minimum event deflection, random and the novel maximum deflection reduction, are simulated crossed with a continuous action space versus the newly introduced discrete action space. To compare the simulated and empirical data, we calculate the behavior distributions in terms of IPA categories and compute the correlations with empirical data, following Heise (2013). Note that in the case of a discrete action space, the EPA labels of the IPA categories (Table 2), i.e. the annotation scheme of the empirical data, are passed as the set of possible discrete actions. In the case of a continuous action space, an observed action is binned to the IPA category to which it has the smallest euclidean distance.
Figure 1 (a) shows the IPA distributions for all observed behaviors and (b) the observed gender differences in these distributions for all simulated model settings and the empirical data respectively. Table 3 summarizes all correlations between simulations and the empirical data set. First of all, we see that for all simulation settings high correlations between simulated behavior distributions and empirical data are achieved.1 This is equally true for the observed differences in behavior between male and female jurors. With a correlation of 0.96, the best agreement between the simulation and empirical data is reached using a discrete action space in combination with the new object selection criterion of maximum deflection reduction.
A discrete action space increases the correlations with the empirical data for all object selection criterions. For the different object selection criteria, we cannot identify a clear "winner" in terms of correlations with the empirical data. But regarding Figure 2, we see that for the newly introduced criterion of maximum deflection reduction, the average level of deflection per agent is indeed notably lower than for the other criteria. There are many factors that influence turn taking. Often, these are task-related and dictated by a sequence of actions in which a task necessarily has to be performed to be completed successfully. They might also depend on cultural conventions or specific role configurations that are not captured in the formalization of ACT as presented here. But if one assumes that agents have full understanding of the affective consequences of their actions and choose their objects in a manner to minimize deflection in the group, then maximum deflection reduction would be the adequate object selection criterion to implement.

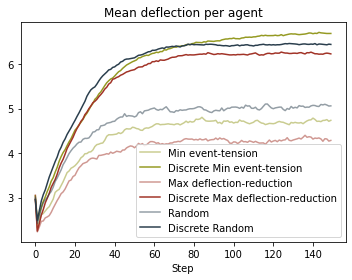
| Simulation setting | Correlations IPA distributions simulations – empirical data | |
| All behaviors | Gender diff. | |
| Min event-tension | 0.87 | 0.85 |
| Dis. min event-tension | 0.93 | 0.90 |
| Max defl.-reduction | 0.88 | 0.85 |
| Dis. max defl.-reduction | 0.96 | 0.90 |
| Random | 0.88 | 0.89 |
| Dis. random | 0.94 | 0.9 |
Restricted group interaction structure: Toy network experiments
In many situations, a group’s interaction structure is restricted such that not every group member interacts with every other. Instead, interaction occurs only along a specific network topology. There are a variety of reasons why this can be the case: the interaction restriction might be by design via a top-down approach, arise from organizational procedures, result from task-specific necessities, or emerge naturally from a given role-identity structure. In real-world scenarios, several reasons might be overlapping and difficult to disentangle when observing interactions. To make the simulation of such groups feasible, we enable the user to model these kinds of restrictions using a static network topology that defines which agent can interact with whom. At a theoretical level, this enhanced model allows one to study the complex interactions between structural and cognitive-affective interdependencies in groups.
In the following simulation experiments, we analyze how a restricted interaction structure influences the situational identities occupied by group members, and the level of affective deflection they experience. To uncover the basic effects of different network topologies, we focus on the least complex group structures possible which still exhibits rich differences in their network properties. Thus, we simulate groups of only three agents. There are in principle 13 different connected and directed network topologies with three nodes, but we need each node to have at least one outgoing edge which means that the agent at that position will have a possibility to act on another agent. Of the remaining 7 topologies, we restrict the experiments to the four networks depicted in Figure 3 because they let us investigate different basic network properties we are interested in. a) is the fully connected base line, b) implies no hierarchy but nodes differ in terms of the number of incoming edges, c) implies a clear hierarchy and d) exhibits transitivity, i.e. a cyclic flow of actions. The remaining three topologies that we don’t analyze here are mere combinations of these basic properties.
In a task group setting, the topologies in Figure 3 might be interpreted as follows: Network a) resembles an egalitarian team in which all group members can act on one another. Network d) also corresponds to an egalitarian group but is best interpreted as a task group in which the task requires circular iterative sequential actions from the team members. In network b), agent 1 occupies a particular position, but it is somewhat ambiguous what that means in terms of status hierarchy since the existing arrows are reciprocal. We could interpret the setting as a formally egalitarian team in which agent 1 is more in demand, and thus more stressed than the other team members. Finally network c) provides a clear status hierarchy in which agent 1 is the leader who directs agents 2 and 3.

To ensure that observed effects result from different network topologies and not from the role-identity structure of the agents, we initialize all 3 agents in each simulation with the same typical fundamental identity of a female2 with an EPA value of \([1.78, 0.83, 0.84]\), but allow for random fluctuations in fundamental and initial transient identities through setting the parameters for individuality and initial tension to \(1.0\). Furthermore, we do not include a group object in this simulation, and in the subsequent toy network simulations for two reasons. First, we are interested in the effects a restricted interaction structure and the related implicit status hierarchy have on group dynamics. We, thus, do not want to blur the effects caused by the network topology by compounding them with actions on the group. Second, in the presence of a restricted interaction structure, it seems implausible that an action on the group object would simply translate in effect to the equivalent of a dyadic action on all group members in equal parts, particularly when the network structure implies a clear status hierarchy.
Figure 4 shows the time series of transient identities, i.e the evaluation, potency and activity values of each agent, and Figure 5 shows the deflection levels for each agent and for each of the 4 interaction structures introduced in Figure 3. All results are averaged over 2000 simulation runs.
In all the plots, we see that after an initial relaxation phase the sentiments quickly approach a stable plateau. This initial relaxation can be interpreted as the agents’ adjustment to the group situation and their negotiation of their role identities in the group setting. In the symmetric network structures a) and d), we see that all agents have on average the same transient identities. This is, of course, what we expect since no agent holds a more advantageous network position, and all agents are on average initialized with the same fundamental identities. We notice that the circular interactions in network d) do not have a noticeable effect (compared to the fully connected network a), on either the transient identities or on the deflection levels of the agents. This finding hinges on the fact that all agents hold the same fundamental role identities, and would otherwise be different if this was not the case.
In the simulations of the asymmetric network structures b and c, the average transient identities as well as the average deflection levels differ among the agents. This clearly indicates that the network topology influences the affective dynamics of the group. In network b, agent 1 can interact with both of the other agents, but she also gets to be acted upon more often than either agents 2 or 3. Being the object of an action more often diminishes the potency of an agent which in return causes higher levels of deflection. In network c, on the other hand, actor 1 can act on both agents 2 and 3 while they can only act on each other. This results in higher E,P and A values for agent 1 which are closer to her fundamental identity, and therefore results in less deflection. Since network c is the only network that has a clear status hierarchy, we conclude that agents whose network positions provide more opportunities to act are able to choose more identity-conforming actions resulting in lower levels of deflection; this effect is particularly pronounced along the potency dimension.


Expectation states theory
Here, we show that the model reproduces well-known theorizing and empirical findings about status dynamics in groups. Expectation states theory (EST) offers an explanation for how status hierarchies form and are reproduced in task groups (for review, see Ridgeway & Smith-Lovin 1999). According to EST, the absence of knowledge about their coworkers’ competence leads team members to take diffuse status characteristics such as race or gender as signifiers of ability, providing some group members with both more opportunities to contribute, and to have their contributions more favorably evaluated because group members are inclined to believe that they are good. Given differences in opportunities, asymmetries in status and prestige can quickly follow. Gender remains an important status characteristic that informs expectations about behavior. These expectations, in turn, organize social relations between men and women that result in system-level inequalities in access to resources and opportunities, resulting in a wide range of economic and social disparities (Ridgeway & Bourg 2004). Status structures in groups can be thought of as the building blocks of these macro-level structural inequalities. For example, to the extent that status processes make it less likely for women in work groups to become and be accepted as leaders, in the aggregate we will observe that more men than women will hold leadership positions in organizations (Correll & Ridgeway 2006).
Our simulation experiment is driven by the hypothesis that the status-related group dynamics described in the EST research program emerge from affect-control mechanisms in the interdependence of individual group members. To develop this argument, we demonstrate in simulation that our implementation of affect control theory in combination with networked interaction structures is capable of reproducing the structural gendered inequality that men are more culturally accepted in leadership positions than women. To this end, we interpret affective deflection in our simulations as a metric for how well cultural expectations are met. We interpret lower average levels of deflection in a group as the group configuration adhering more closely to cultural norms.
The experimental setup is as follows: We simulate task groups of three agents with an interaction structure corresponding to network c) from the previous section which exhibits a clear status hierarchy of one agent in a leadership position and two agents with an equally subordinate status. We are interested in the interplay between status and gender in a setting when group members have no prior explicit knowledge about the actual merit or competence of their team members. We model this by simulating mixed groups of simple female (\(EPA = [1.78, 0.83, 0.84]\)) and male (\(EPA = [1.07, 2.01, 1.05]\)) identities without additional identity modifiers that mark competence (EPA values come from data collected from U.S. undergraduates in 2014: http://research.franklin.uga.edu/act/usa-2015). We then systematically vary which identity is in the leadership position and which gender constitutes the majority of the group. This results in 4 experiments with different setups: 1. A male leader with two female subordinate coworkers. 2. A female leader with one female and male subordinate each. 3. A male leader with one female and male subordinate each, and 4. A female leader with two male subordinate coworkers.
Figure 6 shows the time series of transient identities; and Figure 7 shows the deflection levels for each agent and for each of the 4 experimental settings. All results are averaged over 2000 simulation runs.
We observe that a male majority in the groups raises the overall level of deflection. This can be attributed to the fact that cultural norms, expressed in the fundamental male identity \(EPA = [1.07, 2.01, 1.05]\), entail the expectation of males to be particularly potent. Universally high potency is difficult to meet in group settings because role performance consists of performing the task while also confirming ones role identities. As subordinates, male agents have few opportunities to do this because they are acted upon far more often than they act, resulting in a loss of potency.
More importantly, we find that a female agent in the leadership position results in significantly higher levels of deflection compared to a group with the same role composition, but with a male leader. This is exactly what expectation states theory asserts. Since leadership is associated with potency and the male identity is culturally framed and thus perceived as being more potent than their female counterparts, male group leaders are culturally more accepted than female leaders in the absence of additional competence markers. People generally try to perform their role identities in accordance with cultural expectations, which in turn explains at least partially, why disparities remain between men and women in executive and upper management positions.


A Real-World Network Example: Online Collaboration on GitHub
In the preceding section, we demonstrated that network restrictions on a group’s interaction structure can influence transient identities and the amount of deflection experienced by agents in different network positions. Subsequently, we investigated the interplay between status encoded in a network structure and diffuse status characteristics such as gender that are implied by the agents’ role identities. In this section, we study the effect of specific status characteristics, how they interact with more realistic networked interaction structures, and what that means for a task group’s management of roles and cultural expectations. A specific status characteristic indicates that a person, regardless of social group, has some instrumentality to the specific task goal at hand.
As a real world example, we examine interaction structures found on GitHub, the world’s largest online platform for social coding and collaborative software development. The open source software community is often described as a skill-based meritocracy (Eckhardt et al. 2014; Scacchi 2007). Although there have been findings of gendered behavior and gender bias (Terrell et al. 2017; Vedres & Vasarhelyi 2019) in open source projects as well, the predominant value system in the community is meritocratic. Major motivational factors for developers to contribute to open source projects are the accumulation of reputational status and peer recognition they receive in return, which leads to strong norms for giving credit to authors where credit is supposedly due. This means that developers in leadership positions are presumably selected based on the quality of their contributions and their commitment to a project. Role assignments are of primary importance for programmers’ task groups because perceptions of competence determine who assumes which role (Bianchi et al. 2012).
In the process of collaborative software development on GitHub, a central interaction between developers is the acceptance and rejection of pull requests (PRs). If a developer wants to contribute to a project, she usually forks it (i.e., creates a local copy of the code base), commits changes to it, and then sends a pull request to the original project. These code changes are subsequently reviewed and discussed within the group. A developer with the necessary administrative rights, often one of the maintainers, then either accepts or rejects the PR. If it is accepted, the changes are merged into the project’s code base. This work flow is an example of a sequential protocol in which the goal of the task group can only be reached when certain actions are performed in a given order. (Zöller et al. 2020) found different types of groups present on Github, categorized in terms of the network topologies spanned by the history of a project’s accepted PRs. The differences in interaction topology corresponded with differences in productivity, popularity, resilience and language use. In order to shed light on the interplay between topology of the interaction structure, status, role expectations and identity management in collaborative online software development, we take two representative example networks (Figure 8) of the most different and clear-cut clusters of this study as the starting point for our analysis. Figure 8 a) shows an example of a complex interaction topology that exhibits clustering, reciprocity, several high-status developers who have the administrative rights to merge PRs, as well as several lower-status contributors who do not have the right to merge PRs. Figure 8 b), in contrast, depicts a very clear-cut hierarchical interaction topology with a single maintainer responsible for merging all of the PRs.

Formalization of the examples
In the example graphs depicted in Figure 8, the directed edges point from the developer who submits to the developer who accepts the PR. But when submitting a PR, a developer does not necessarily know in advance who is going to review it. Hence, to simulate the network structure, we reverse all edges because accepting a PR is without a doubt a directed action towards the submitter while submitting a PR is more accurately modeled as an action on the whole group. Therefore, we include a group object in this simulation setup and allow actions on the group.
Although the network structures at hand were derived from accepted PRs, we assume that the majority of actions are carried out along the same topology. We, thus, feed the adjacency matrices of the reversed graphs into our model as restrictions that govern both pull-requests and group discussion. During the group discussion, actions on the group object are possible in order to adress the whole group. Note that we ignore any occuring self loops.3
In the simulation, we want to mimic the sequence of actions we observe in real Github repositories, i.e. the sequence of submitting a PR, discussing it in the group and it being accepted or rejected by a maintainer. We, therefore, enforce a cyclic protocol in the model that consists of the following sequential actions: 1. An agent submits a PR which is interpreted as an action on the group. 2. The group discusses the PR. This is simulated via a sequence of freely chosen actions that are performed along the network topology or on the group object. The length of the sequence is determined randomly to be between 0 and 10 actions. 3. An agent with merge rights who shares a link with the submitter (specified via the network topology), either accepts or rejects the PR. The agent that actually gets to act is the one that experiences the most deflection among the candidates that come into consideration.
To obtain the EPA labels of relevant concepts in the subculture of software developers, we conducted a mini-survey among \(N=17\) proven Github users,4 in which participants rated concepts along all three dimensions on a continuous scale ranging from \(-4.3\) to \(+4.3\). The resulting mean EPA values for these concepts are shown in Table 4.
| Concept | E | P | A | |||
| mean | std | mean | std | mean | std | |
| developer | 1.79 | 1.01 | 1.37 | 1.04 | 1.17 | 1.07 |
| novice developer | 0.70 | 0.88 | -0.98 | 1.05 | 0.42 | 1.28 |
| experienced developer | 1.82 | 1.20 | 2.46 | 0.51 | 1.51 | 0.88 |
| submit pull request | 1.82 | 1.24 | 0.29 | 1.75 | 1.03 | 1.48 |
| accept pull request | 2.13 | 0.95 | 1.64 | 1.27 | 0.78 | 1.50 |
| reject pull request | -1.37 | 1.17 | 2.01 | 1.01 | 1.33 | 1.14 |
To investigate the interplay between specific status characteristics that are encoded in role identities, network positions that imply status, and cultural expectations that mediate between the two, we essentially run four different experiments for each network structure in Figure 8.
- All agents are initialized with the fundamental identity of "experienced developer".
- All agents are initialized with the fundamental identity of "novice developer".
- All agents who have higher status and can accept PRs ( i.e. who have an incoming edge in Figure 8) are initialized with the fundamental identity of "experienced developer". All other agents are initialized with the fundamental identity "novice developer".
- Agents are randomly initialized with either the identity "experienced developer" or "novice developer" independent of their network position, but with the same numbers of experienced/novice developers as in setup c).
For all four conditions, we set the action-on-group rate and reciprocity rate to zero to have as little overlapping/distracting additional effects as possible. Furthermore, when initializing the model, fundamental identities are drawn from a clipped normal distribution with standard deviation (individuality) 1.0, centered on the target fundamental. All results shown in the subsequent section are averaged over 5000 model runs for each experimental setup.
Results
Figure 9 shows the average transient identity profiles, and Figure 10 the average deflection of the agents at different network positions of the star-shaped topology for the simulations of the four experiments described in the previous section. Similarly, Figure 11 shows the average transients, and Figure 12 the average deflection for simulations of the complex network structure.
In the star shaped interaction topology, there is only one project maintainer with a clear network advantage that is higher in status and 8 contributors that have all the same symmetrical network positions with lower status. We see from Figure 9 a) and b) that whether we simulate a group of experienced developers or a group of novice developers, in both cases the developer in the high status network position (agent 1) exhibits a higher value of potency. However, Figures 10 a) and b) reveal that, for experienced developers, this increase in potency leads to less deflection while for novice developers it leads to more deflection. The reason for this is that an increased potency aligns more closely with the potent fundamental identity of the experienced developer while it is not role-confirming for the novice developer.
The simulation results suggest that experienced developers experience more deflection than novice developers which holds true for both the star-shaped topology and the more complex interaction structure. In an ACT simulation framework, this is generally the case for agents with more potent identities because they experience a higher level of deflection when acted upon or when they are unable to perform role conforming behavior on less potent agents. Therefore, to illuminate the interplay of role identities with network positions, we keep the simulation settings as comparable as possible in experiments c) and d) and include the same number of experienced and novice developers in the groups.
From Figure 9 c) for the shar-shaped network and from Figure 11 c) for the complex topology, we see that matching the status positions in the network with the role identities, i.e the experienced developers with the the high status positions and the novice developers with the low status positions, leads to much higher potency for the experienced developers compared to experiment a). For the complex network in Figure 11 c), we see an additional splitting of the transient identities, which is produced by the different centralities of the node positions. Unexpectedly, agent 1 exhibits lower potency than the other experienced developers in high status network positions, even though no other agent can directly act on her. The reason for this finding is that agent 1 can only directly act on agent 0 who is also an experienced developer. Because agents try through their actions not only to confirm their own identity but also the identities of the others, agent 1 has to routinely compromise by choosing actions that lead to lower potency and higher evaluation and activity values than would be the case if agent 0 was inexperienced. The potency of agent 0, in return, is lowered as well because she is acted upon regularly by agent 1. For both agents 0 and 1, this translates into slightly higher deflection values which can be seen in Figure 12 c). This interplay is a nice example of the complex, non-linear dynamics that can quickly arise in affective space when modeling complex role-identity and network cofigurations.
Compared to experiment d) in which the agents are randomly assigned to network positions, the matching in experiment c) leads to a lower mean deflection in the group when averaged over the deflection of all agents. This holds true for the star-shaped topology (Figure 10) and for the more complex interaction network (Figure 12) where the effect is even stronger due to the more balanced numbers of experienced and novice developers in the group. Comparing the two group cofigurations, lower average deflection levels in one group signify that the assignment of role identities to network positions is culturally more accepted in this group than in the other. Hence, the simulations confirm the repeated statements in the literature that meritocratic values in the form of deference to experienced skilled individuals plays a strong role in the open source software development community. This result may seem trivial, since it might be considered common sense that experienced developers are culturally more accepted in leadership positions than novice developers. However, our model sheds light on how these cultural expectations arise. Specific (and diffuse) status characteristics translate into role identities that imply normative affective meanings. People then choose their actions according to cultural norms, and in such a way as to perform their role identity to confirm its affective meaning, as well as to confirm the affective meanings of the role identities of their fellow team members. Furthermore, the simulations demonstrate that affect control theory as a generic social theory in combination with networked interaction structures and protocol sequences is capable of sensibly reproducing observations from specific occupational fields such as software development.




Summary and Discussion
In this work, we developed and implemented an agent-based model to simulate interactions in complex task groups in constrained environments. To this end, we extended an existing model based on affect control theory by Heise (2013) in three important ways. First, we allow the analyst to specify a network topology that restricts possible action pathways in the group which can be used to model hierarchical role configurations. This extension was motivated by observations in online task groups whose interactions occurred solely along network structures. Second, we allow the analyst to specify a discrete set of actions for agents to choose from, which caters to the fact that in many group situations only a limited number of behaviors are admissible, acceptable or available. Third, we allow the analyst to specify sequences of actions that have to be carried out in order. These protocols are often observed in task groups where the completion of a task requires several steps of role-based division of labor.
In a series of simulations, we found that network positions have an influence on agents’ experienced affective deflection and their transient identities, particularly along the dimension of potency. This finding highlights the interconnection between structural properties of groups and group members’ cognitive-affective representations of group interactions. By expressing status hierarchies in terms of node positions in a network topology and interpreting deflection as a metric for cultural acceptance, we were able to build a bridge between expectations states theory and affect control theory that can contribute to new theoretical developments in both literatures. In particular, we succeeded at reproducing central results from the expectation states framework (Ridgeway 2019) in simulations of groups whose actions were driven by the affect control principle. The simulations of idealized, mixed-gender task groups suggested that, regardless of actual competence, men were on average culturally more accepted in leadership positions than women, which in the simulations could be traced back to the encoding of cultural norms in affective identity labels. Agents chose their behaviors in such a way as to align them with the cultural expectation from the group towards their role identity, but for female agents in leadership positions the average deflection in the group was significantly higher compared to male agents in leadership positions. This result suggests that in order to promote gender equality sustainably, the cultural norms in which female identity is generally perceived to be less powerful and more positive than the male identity would have to be adjusted. From a symbolic interactionist point of view, cultural meanings arise and are consolidated through interactions. Consequently, by continuously promoting and normalizing female leadership and by increasing its visibility, the perception of the normative female identity can possibly be changed in the long-term future through changes in the cultural affective meanings of female identities.
As an example of a realistic complex task group, we modeled in a series of experiments groups consisting of open source software developers with their domain-specific work flows. We extracted network structures from GitHub, the largest platform for open source software development, and conducted a small survey among verified Github users in which we had the most important role identities and task related behaviors rated on affective scales. This subculture and domain-specific data served as an empirical basis to parameterize the simulation model. The simulations showed that in these groups average deflection was significantly lower if high-status network positions, signifying more responsibility and the power to accept or reject proposed changes to the code base, were filled with experienced developers instead of novice developers. This result is in accordance with the presumed meritocratic value system in the open source software development community, which is essential for the process of self-organization in groups that are not backed by a larger organization.
We believe that this is a good example for how our model can be adapted and generalized to the study of groups in other domains and subcultures which we think is a promising use case of the model for future research. An adaptation process will generally consist of the following steps. First, one will have to research the task domain and its subculture of the groups of interest. This might include the identification of an organizational structure that typically guides group interactions. Furthermore, this is likely to include the identification of important role identities and behavior sequences that are characteristic or necessary for completing core tasks or conducting other focal interaction protocols in the group. Second, one can then design a mini-survey to collect affective ratings of these concepts. These empirical findings can subsequently be injected into the simulation setup which can then be used to illuminate the affective group dynamics, generate hypotheses, or compare different role constellations. In this way, it is possible to systematically analyze the interplay between status characteristics, role identities, and cultural norms and expectations.
There are several limitations in our model that we briefly want to discuss: The ACT equations are derived from dyadic vignettes, but have not been tested empirically in group settings (Heise 2007). We assume that as long as the actions in a group are mostly of a dyadic nature, our model will be accurate, but corrections to the theory and model implementation might be necessary in groups where the focus is on the collective aspects of the group like joint behaviors by or on several agents or towards the group as a whole. In this context, the implementation of the group object should also be reviewed. We followed Heise (2013) in how we implemented the group object as a pseudo-agent, but we have the impression that both ACT as a theory as well as its implementation in a simulation model would benefit from a rigorous empirical investigation about how to formalize the group identity within an ACT framework.
Another consequence of the dyadic structure of ACT’s impresssion change equations is that the theory originally did not include propositions about the mechanisms that guide turn taking. Like Heise, we assumed for the most part that taking the initiative to act was guided by deflection levels and only in the simulation of Github groups sometimes the actor was determined by other factors like the administrative rights encoded in the network structure. Note that we tried to shed some light on the differences between possible object selection criteria in the reproduction of the jury simulation experiments, but we did not find tremendous differences in the agreement with the available empirical data set between the different criteria. But the amount of available empirical data was both limited and domain-specific. What we did find, however, was that the newly introduced object selection criterion of maximum deflection reduction did significantly reduce deflection in the group. In any case, we believe that the mechanics of turn taking in groups and its interplay with ACT should be further investigated. This includes the specific micro-interactions group members use to negotiate and signal who is the next person to act. Our current model implementation, where each group member has full and consensual information about each other group member’s state of mind is clearly unrealistic given the bounded rationality of the human brain. A more realistic assumption would be a social-comparison mechanism where the tension experienced by a group member translates into nonverbal cues which are then recognized by other agents, but it remains for future work to model such a mechanism. In addition, a group member’s ability to recognize and understand affective group dynamics might vary and depend on each individual’s communication skills and ability to empathize with others, which are related to the "collective intelligence" (Woolley et al. 2015) of the group as a whole.
An interesting step in the direction of modeling individual differences not only in terms of agents’ observations but also in terms of agents’ ability to manage several roles simultaneously is Bayesian affect control theory (Schröder et al. 2016), which models dyadic interactions via partially observable Markov decision processes. Observations might also play a role in turn taking. It is plausible to imagine group situations in which a group member might intervene and take the initiative after observing the actions of other group members even when they have not been the target of any action themselves.
In addition, affect control theorists have started to model the interplay of identity maintenance processes and other goals (Hoey, MacKinnon, and Schröder 2021); this work has important implications for modeling task groups as group members frequently must balance between meeting immediate task goals, advancing their own social status, and ensuring the group’s mid to long-term functioning by supporting both the group’s collective identity and the identities of the group members. Successful identity performance is critical to leveraging social capital at a later point in time, which means that affirming and seeking advancement are not necessarily mutually exclusive. However, we believe that the two processes operate on different time scales. While our model is designed to simulate situational task group settings, an agent’s career advancement is an important long-term strategic goal that is currently not taken into account. The amount of tension between these different objectives is largely influenced by whether personal long-term goals align with the goals of the group. Future group models will ideally include a utility function that enables the modeling of several kinds of objectives and time scales.
Most of the aforementioned limitations could be systematically addressed with a series of networked online experiments that monitor group interaction processes while at the same time controlling the experimental conditions. Combined with a survey among participants this would be a promising branch of future research that could both advance theoretical aspects of group processes research, and at the same time provide an invaluable source of data to directly evaluate simulation models.
Model Documentation
The ACTING model was implemented in Python 3.6 using the Mesa library for ABM (Masad & Kazil 2015), and the source code for the model and Jupyter notebooks with all simulations presented in this article can be found at https://github.com/nikozoe/ACTING. The source code is also available through the CoMSES Computational Model Library as: ACTING (Affect Control Theory based simulation of Interaction in Networked Groups)" (Version 1.0.0), https://www.comses.net/codebases/fe554877-a041-4fb4-91e5-8400ebec573c/releases/1.0.0/.Notes
- Note that while implementing the model in Python we discovered a bug in the implementation of the object selection that was present in Heise’s original Netlogo version of group simulator. This bug by coincidence slightly increased the correlation between experimental data and Heise’s simulation results (min-event-tension + continuous action space Heise (2013)). After the fix, this correlation dropped from 0.91 for all behaviors and 0.92 for the gender differences to 0.87 and 0.85, respectively. We conjecture that Heise calibrated the other parameters, i.e. action-on-group rate and reciprocity rate such as to maximize this correlation, which would explain the drop after the fix.
- For this example, the type of identity we model is not important because our goal here is to isolate the effect that the network topology has on the agents’ transient identities and deflection levels.
- Self loops correspond to developers merging their own pull requests.
- While N=17 might seem small, note that we are measuring cultural consensus not variation. The error on the mean sentiment is reduced by a factor of \(1/\sqrt{N}*\) compared to an individual rating. Standard deviations of 1.6 on Evaluation, 1.7 on Potency, and 1.8 on Activity are reasonable general estimates of error when a single respondent is being employed to assess cultural sentiments (Heise 2010).
Appendix: Complete ODD Protocol of the ACTING Model
The agent-based model presented here is named ACTING (Affect Control Theory based simulations of Interaction in Networked Groups). The model was implemented in python using the mesa library for ABM (Masad & Kazil 2015), and the source code for the model and Jupyter notebooks with all simulations presented in this article can be found at https://github.com/nikozoe/ACTING. In the subsequent description of the model, we follow the ODD protocol (Grimm et al. 2020).
Purpose and patterns
The purpose of this model is to simulate task group interactions in order to understand and analyze the interplay between role identities, role expectations, status hierarchies, and the group’s interaction structure. A specific purpose of the model is to explain which team members are more or less likely to occupy high status positions based on their role identities. The formalization of how the effort to maintain role identities translates into role expectations and behaviors is guided by affect control theory (ACT). Thus, another purpose of the model is to bridge the sociological theories of ACT and status characteristics.
The patterns used to assess the model’s ability are two-fold. On the one hand, the model is able to reproduce empirical behavior distributions. The model is a modification and extension of an existing model (Heise 2013) that was able to accurately predict behavior distributions of jury deliberations and also gender differences in these behaviors. On the other hand, the model explains the phenomenon of status allocation and the formation of status hierarchies in groups. It is able to reproduce empirical findings about gender differences in status allocation in task groups (Ridgeway 2019; Ridgeway & Bourg 2004). The model is also able to link status allocation in groups of open source software developers to meritocratic principles, a finding that has been emphasized by various researchers (Eckhardt et al. 2014; Scacchi 2007).
The model is grounded in empirical data and it is adaptable to task groups that operate in specific subcultures. For this purpose, a small survey has to be conducted to obtain ratings of central role identities and behaviors. We demonstrate this process by modeling teams of open source software developers, where the interaction structures are derived from empirical observations (blinded reference).
Entities, state variables, and scales
The following entities are included in the model: agents which represent members of a task group, a group object (optional) which represents the group identity, and the global environment which is either provided by the GroupModel or, if the group is following protocols, by the ProtocolGroupModel. In our Python implementation, the latter two are formally derived from the Model class of the mesa package (Masad & Kazil 2015). An overview about all entities and their state variables can be found in Table 5.
| Variable name | Variable type | Meaning |
|---|---|---|
| GroupMember | ||
| F | \([\)real, real, real\(]\), static | Fundamental identity consisting of three values in the dimensions Evaluation, Potency, Activity (EPA) |
| T | \([\)real, real, real\(]\), dynamic | Transient identity consisting of three values in the EPA dimensions |
| acting | boolean, dynamic | True if is acting at current time step |
| Group | ||
| F | \([\)real, real, real\(]\), static | Fundamental identity consisting of three values in the EPA dimensions |
| T | \([\)real, real, real\(]\), dynamic | Transient identity consisting of three values in the EPA dimensions |
| GroupModel | ||
| schedule | object, dynamic | keeps track of the current time step. Also keeps track of the agents whose order is shuffled randomly at each step. |
| actor | GroupMember, dynamic | Reference to group member who gets to act at current time step |
| object | GroupMember or Group, dynamic | Reference to group member who is acted upon at current time step |
| action | [real,real,real], dynamic | Behavior at current time step consisting of three values in the EPA dimensions |
| datacollector | object, dynamic | collects agent and model data for later retrieval |
| ProtocolGroupModel If the task group is following a protocol, ProtocolGroupModel is instantiated instead of GroupModel from which it inherits. That means all state variables listed under Group Model are also state variables of ProtocolGroupModel. |
||
| n_iterations | int, dynamic | specifies the length in time steps of the current protocol part. |
| select_actor | string, dynamic | Optional, is interpreted as python code and overwrites the select_actor method from the GroupModel |
| code | (string,string), dynamic | Optional, is interpreted as python code. code[0] is executed before the current protocol part; code[1] is executed after the current protocol part. |
| Parameters of GroupModel that become state variables of ProtocolGroupModel | ||
| reciprocity_rate | float, static | Probabilty for an action to be reciprocal |
| object_choice | string, static | mechanism by which the object (agent who is acted upon) is chosen. Options are min event-tension,max deflection-reduction or random. |
| action_on_group | Boolean, static | Sets whether actions on the whole group are possible. |
| group_action_rate | float, static | Sets the propability for an action to be on the whole group. Only makes sense if action_on_group is True. |
| network_structure | Matrix with entries 1 and 0, static | Adjacency matrix of a network graph that determines who can act on whom |
| data_model | string, static | Determines which set of empirical coefficients is used in the ACT impression formation equations. Options are: us_unisex, us_male, us_female, canada_unisex, canada_male, canada_female, china_unisex, ger_unisex |
| discrete_actions | list of floats, dynamic | List of possible actions. Each action is parsed as a list of EPA values. |
Group members
All agents in the model are initialized with a fundamental identity \(F\), which remains constant during a simulation run, and an event-driven transient identity, \(\tau\), which changes through interactions with other agents in the group. Both consist of 3-dimensional arrays \([E, P, A]\) with values for evaluation, potency and activity. An agent’s deflection \(d = (F-\tau)^2\) represents the affective dissonance an agent experiences between their situational and their fundamental identity.
Group object
Lawler et al. (2000) finds that emotions produced through the interactions of group members are attributed in part to relevant social units. The group identity consequently forms over time through repeated and consistent interactions between its members. Depending on which kind of a group situation one wants to model, it may or may not be sensible to include a group object. Therefore, our implementation of the model makes the integration of a group object optional. If included, it is simulated as a pseudo agent that like the group members holds a fundamental and a transient identity. The group object can be acted upon, but can not act itself.
GroupModel
The entity GroupModel controls the global environment. In our implementation, it inherits from the Model class of the Python package Mesa. Its state variables are: 1. schedule, which keeps track of the current time step and the order of agents at each time step. 2. actor, 3. object and 4. action which hold references to the respective group members and the behavior performed at the current time step. 5. The datacollector which collects data at the end of each time step (see Observation in the Design concepts section).
The GroupModel is initialized with several parameters that are described in later subsections.
ProtocolGroupModel
If the group in the simulation is following a protocol, the global environment is controlled by the ProtocolGroupModel instead of the GroupModel. ProcolGroupModel inherits from GroupModel, therefore, it has all its state variables. The ProtocolGroupModel lets the researcher define a protocol in which the global environment changes over time. Formally, this turns all parameters that are present in the GroupModel into state variables in the ProtocolGroupModel. Most importantly, this allows one to change the behaviors available to group members for each section of the protocol through the ‘discrete_actions’ parameter. Furthermore, it lets the modeler specify through the parameters ‘action_on_group’ and ’group_action_rate whether and with which probability actions in a certain protocol section can be performed towards the whole group rather than towards a specific agent. In addition to all parameters already present in the GroupModel, there are three new state variables, two of which are optional:
- n_iterations (mandatory): changes with each part of the protocol and specifies the duration of that part in time steps.
- select_actor (optional): if specified, overwrites the select_actor submodule for that part of the protocol.
- code (optional): custom code that is executed before or after the respective part of the protocol.
This makes the ProtocolGroupModel very general and expressive, so that it can be adapted to specific work flows of specialized task groups.
Scales
The model represents time. Each time step corresponds to an action that is performed by one of the group members. The model does not represent physical space, but it represents EPA space in which fundamental and transient identities of agents are located as well as behaviors.
Process overview and scheduling
GroupModel
After initialization, the simulation adheres to the following process:
- The GroupModel executes the select_actor submodel. There is a chance that the action is reciprocal with probability reciprocity_rate. If so, the actor is the object of the last action. Otherwise the GroupMember with the highest deflection is selected and assigned to the state variable actor. The actor’s state variable acting is set to true.
- The environment increases the time step in the schedule by 1.
- The group member who has been selected as the actor executes the act submodel, which includes:
- The object and the behavior are determined. There is a chance that the action is directed towards the Group object (if defined) determined by the model parameter group_action_rate. If the action is supposed to be reciprocal or directed towards the group then the object is already known and the behavior is determined via the submodel compute_opt_behavior. Otherwise, the object and behavior are determined via the submodel find_best_object_and_behavior which determines the object according to ACT, only considering possible interaction pathways defined in the model parameter network_structure. The GroupModel’s state variables object and action are updated.
- The submodule compute_transients calculates how the action changes the transient identities of the actor and the object. For the actor and the object, the transient state variable, T, is updated accordingly as well as the value for deflection via the submodel update_deflection. If the object is the Group, then all group members except the actor experience the action as if they had been the object and their transients are updated via the submodule compute_transients.
- The datacollector stores the current values of the state variables: actor, object, action and reciprocal as well as the transient identities T and the current deflection of each group member.
ProtocolGroupModel
The ProtocolGroupModel is best understood as a sequence of GroupModels. For each part of the protocol, the group and its members remain the same but the parameters of the GroupModel are changed according to a protocol with which the model is initialized. In the following, the process for one protocol segment is described:
- All GroupModel parameters that may now be state variables are set at the beginning of the protocol step.
- If the state variable code is defined, then code[0] is interpreted as Python code and executed.
- For n_iterations time steps, the process is exactly as described before for GroupModel. If the state variable select_actor is defined, it is used in place of the submodel select_actor.
- If the state variable code is defined, then code[1] is interpreted as Python code and executed.
- The next protocol step begins. If the last protocol step is reached and the total simulation time exceeds the sum of n_iterations for each step, then the protocol starts from the beginning.
Discussion
ProtocolGroupModel has been designed to be as expressive as possible. Therefore, it has the additional state variables code and select_actor so that it can be adapted to all kinds of work flows even if they are more complicated than mere sequences of different behaviors. While in principle all parameters of GroupModel become state variables in ProtocolGroupModel, in most simulations only a few of these will change. Most commonly, the parameter discrete_actions allows one to enforce sequential behaviors; i.e., the order in which actions have to be performed in a certain work flow.
In our example of modeling the work flow of software developers, this lets us easily define a protocol with three steps consisting of different behaviors that have to follow each other: 1. A code contribution is proposed. 2. Group members discuss. 3. The code contribution is accepted or rejected. The state variable code is used to keep track of the group member that contributed code in part 1 so that this information can be used in part 3. The select_actor is used to select actors in part 1 and 3 of the protocol depending on their network position.
Design concepts
Basic principles
The model, modifying and extending Heise’s (2013) Group Simulator, conceptualizes a small group as a "team" in which individuals are committed to helping each other maintain their identities. The formalization of how this effort to maintain role identities translates in role expectations and behaviors is guided by Affect Control Theory, a mathematically specified theory of symbolic interaction (Heise 2007).
An event in ACT consists of an actor A that directs a behavior B towards an object O. After an event, the transients of actor, object and behavior are changed according to the empirically parameterized impression formation equations 1, 2 and 3 previously shown in Section 3.12.
Emergence
Emerging properties of the model are the transient identities and the behavior of each agent. When the transients deviate from the respective fundamental identities, the agents experience deflection. We interpret the average amount of deflection in a group as an emergent metric for the cultural acceptance or rejection of the group setting (or role set), where the setting consists of the member’s role identities, network structure, and available behaviors.
Adaptation
The behavior of group members is adaptive in the sense that their urge to act is driven by the amount of deflection they experience. Also group members adapt which action they choose on a given turn and whom they direct it towards by considering what effect their action would have on their own and on the object’s deflection levels.
Objectives
The agents’ objective is to choose the action that will most confirm their own fundamental identity and the fundamental identities of others. In this regard, the model follows the ACT principle stating that people seek to verify cultural knowledge about the social order (Heise 2007). See Equations 5 and 6 and further details in Section 3.11.
Learning
Learning is not represented in the model. It is rather assumed that agents have already learned cultural meanings of identities and behaviors before entering the task group situation, and therefore have a shared understanding of these concepts.
Prediction
If the environment parameter discrete_actions is defined, it holds a limited number of behaviors that group members can perform. To choose a behavior, an actor will predict the amount of deflection each behavior would cause and pick the one that causes the least. When there is no restriction on the action space, this prediction is done implicitly by solving the optimization problem stated in equation (???): appendix-optimization.
Sensing
In ACT, agents can theoretically only sense behavior clues such as facial expressions from which they infer mental representations of the identities of others. We do not model this process, but assume in an idealized and simplified manner that the agents’ capability of inference includes all transient identities of all group members and the resulting deflection can be perceived by all others. This information then influences actor, object, and behavior selection.
Interaction
Actor and object selection: In each step of a simulation run, only one actor gets to act on one object which is either another agent or, if applicable, the group object. When an actor and an object are determined and their fundamental and transient identities are known, ACT provides a framework to calculate the optimal behavior which follows cultural norms, preserves role identities, and minimizes affective dissonance to the greatest possible extent (see Objectives). However, ACT provides no clear guidance on how to select an actor or an object in a group setting. This is not surprising since the ACT equations are derived from dyadic vignette experiments. Realistically, who acts upon whom in task groups is often task specific. Nonetheless, we assume that affective reasoning influences actor and object selection because it has an effect on the amount of affective dissonance experienced within the group which agents seek to minimize as per affect control theory’s control principle.
In our model, we follow Heise (2013) and assume that the agent who experiences the most deflection will be the next to act. This means that affective dissonance is the only driving force in turn-taking, which in the absence of task-specific information seems sensible. There are other options available in the model implementation like for example random actor selection that might be more accurate depending on the group and the task one wants to model.
After an actor is determined, the object selection criterion regulates how the object that the actor will act upon is chosen. One possible criterion is minimum event tension which was also used in Heise’s (2013) study to model juries. The minimum event tension criterion works as follows: once the actor is set, for each object candidate the optimal behavior is determined according to ACT. Subsequently, the action is carried out hypothetically and the resulting after-event deflection is calculated, which involves only the fundamentals and the transients after the event for the actor, object and behavior. Finally, the actual object is chosen so that this after-event deflection is minimized.
The minimum event tension criterion has the short-coming that it only considers the situational deflection of the actor, object and behavior triple after the event. However, Heise points out himself in the article (Heise 2013) introducing his original model that it aims at integrating Goffman’s (1959) suggestion that "a small group operates as a team in which individuals are committed to helping each other maintain their identities (faces)". Furthermore, Heise claims that "an individual motivated to action selects as object the group member who provides an optimal basis for creating a tension-reducing action that will confirm the fundamental affective meanings of actor and object". However, this tension reduction is not properly taken into account by the minimum event tension criterion. We therefore introduce a different object selection criterion that, in our opinion, adheres even more closely to the control principle. We term the criterion maximum deflection reduction, because it tries to reduce overall affective deflection instead of only causing a minimally deflective event. It works as follows: once the actor is set, for each object candidate the optimal behavior is determined based on ACT’s impression change equations and subsequently the hypothetical after-event deflection is calculated. But this is now compared to the overall deflection before the event from which the after after-event deflection is subtracted. Object and behavior are then chosen such as to maximize this difference, i.e. the deflection reduction. This means that both the transient identities and the overall deflection before the event are taken into account.
Action space: Past ACT models have assumed a continuous connotative action space along the dimensions evaluation, potency and activity, where each point can be mapped to a denotative label, i.e. the name of a behavior in natural language. In our model, the user can specify either a continuous action space, or define a discrete and finite set of possible actions. A discrete action space can be helpful in at least three ways. First, empirical data is often annotated using categorical taxonomies to describe the observed actions (Bales 1950). Although other behaviors might be possible, it is sensible to restrict simulation behaviors to the empirical annotation scheme in order to increase comparability. Second, there is a binning problem when mapping back in hindsight from connotative space to a categorical behavior set in denotative space because the volume that is mapped to each behavior might vary. This in return can lead to biased behavior distributions. Third, in many situations, agents simply only have a limited set of actions at their disposal. This might be due to institutional procedures or limited capabilities that are not captured by role identities. An obvious example where this is the case is the digital sphere. Behaviors might simply be restricted by a graphical user interface or a limited set of possible actions in an application. In our implementation, the action space is limited through passing a list of allowed behaviors in the environment parameter discrete_actions.
Interaction structure: In the model, the default setting is that every agent can act on every other agent. But, in many real world situations, who can interact with whom is governed by institutional hierarchies or organizational procedures. Therefore, the user can impose restrictions on who can interact with whom through passing the model a network structure in the form of an adjacency matrix. This means that an agent can only act on another agent if there exists a directed edge from the former to the latter in the network.
Protocols: Many task groups are structured by sequential protocols in which some actions necessarily have to follow others in order to complete a task. To allow for a realistic simulation of these groups, we include the possibility to parse such a protocol to the model in the form of a list in which each item represents one part of the protocol. What behaviors are available and how many actions should be carried out is specified for each step. Optionally, different settings for model parameters can be parsed before the beginning of each part as well as custom python code that should be executed before or after the protocol step. This flexibility makes the model expressive and allows one to customize the simulations to specific tasks and work flows of interest.
Stochasticity
At the beginning of a simulation, group members’ fundamental and transient identities are initialized stochastically through parameters individuality and initial_tension (see Initialization). Furthermore, the rate of reciprocal actions and actions directed towards the group may be set through the parameters group_action_rate and reciprocity_rate. Setting these parameters can make sense for simulating certain kinds of task groups where these rates have been observed empirically but are not automatically reproduced by the implemented turn taking mechanisms. Finally, stochasticity may enter a simulation if the length of a protocol part n_iterations is specified as a range. It is then set to a number in that range which is randomly sampled with equal probabilities for all numbers.
Collectives
The group entity, if specified, represents an explicit collective entity since it is typically initialized with the average fundamental and transient identity of all group members and an action towards the group entity affects all group members simultaneously. Furthermore, we regard the average amount of deflection of all group members as an important collective property. It can be interpreted as an emergent metric for the cultural acceptance or rejection of the group setting (or role set), which consists of the member’s role identities, the pathways of interaction specified by the network structure, and the behaviors that are available to the agents. This holds true particularly when comparing the simulation results of different group settings.
Observation
At the end of each time step, the datacollector stores data for later retrieval and analysis. It collects the current values of the environment state variables actor, object, action and reciprocal as well as the transient identities \(\tau\) and the current deflection of each group member.
Initialization
The explanation of the initialization is intended to be generic, and initialization may differ among simulation scenarios.
When initializing the desired number of agents at the beginning of a simulation run, two parameters can be passed along with the fundamental identity \(\tilde{F}\), namely individuality \(i\) and initial tension \(t_i\). When individuality \(i\) is set, the fundamental identity \(F\) is drawn from a clipped normal distribution centered around \(\tilde{F}\) with a standard deviation of \(i\), otherwise \(F = \tilde{F}\). This accounts for the fact that there is individual variation within role identities. For example, all group leaders will tend to feel powerful, but some more than others. When initial tension \(t_i\) is set, the initial transient identity \(\tau\) is drawn from a clipped normal distribution centered around \(F\) with a standard deviation \(t_i\). This accounts for variation in tension among group members as they enter a group situation. For example, a new group leader might initially feel apprehensive rather than powerful. If \(t_i\) is not set, \(\tau\) is initialized with the same value as \(F\).
The group identity can be initialized explicitly with EPA values depending on what type of group is modeled. As a default, it is assigned the average of the identities of all agents in the group at the beginning of the simulation.
Input data
When modeling task groups that follow a protocol, this protocol is parsed as input data to the ProtocolGroupModel at initialization. It specifies how the environment is changed for the different parts of the protocol. In Section 5.6 of the main text, we discuss the work flow of software developers presented as an example.
Submodels
update_deflection – updates the deflection for each agent according to \(D = (F - \boldsymbol{\tau}_{aft})^2\).
compute_opt_behavior – Given the actor and the object, the function finds the behavior that minimizes deflection by solving the optimization problem posed in Equation 5. If the action space is restricted, it searches only among the available actions.
find_best_object_and_behavior: Given the actor, finds best object and behavior applying compute_opt_behavior to all object candidates and taking the network structure of behavior pathways into account.
compute_transients – Given an event specified by actor, object and behavior, the function computes how the transient identities change according to the impression formation Equation 3.
For more information on the mathematical details, see Mathematics of Affect Control Control theory in Heise’s book Expressive Order (Heise 2007).
References
AMBRASAT, J., von Scheve, C., Conrad, M., Schauenburg, G., & Schröder, T. (2014). Consensus and stratification in the affective meaning of human sociality. Proceedings of the National Academy of Sciences, 111(22), 8001–8006. [doi:10.1073/pnas.1313321111]
AVERETT, C., & Heise, D. R. (1987). Modified social identities: Amalgamations, attributions, and emotions. The Journal of Mathematical Sociology, 13(1–2), 103–132. [doi:10.1080/0022250x.1987.9990028]
BALES, R. F. (1950). Interaction process analysis: A method for the study of small groups. Cambridge, MA: Addison-Wesley Press.
BALES, R. F. (1953). The equilibrium problem in small groups. Working Papers in the Theory of Action.
BALES, R. F., & Slater, P. E. (1955). 'Role differentiation in small decision-making groups.' In R. Bales & T. Parsons (Eds.), Family, Socialization and Interaction Process, (pp. 259–306). Free Press Glencoe.
BALES, R. F., & Strodtbeck, F. L. (1951). Phases in group problem-solving. Journal of Abnormal and Social Psychology, 46(4), 485–495. [doi:10.1037/h0059886]
BERGER, J., Cohen, B. P., & Zelditch, M. (1972). Status characteristics and social interaction. American Sociological Review, 37(3), 241–255. [doi:10.2307/2093465]
BIANCHI, A. J., Kang, S. M., & Stewart, D. (2012). The organizational selection of status characteristics: Status evaluations in an open source community. Organization Science, 23(2), 341–354. [doi:10.1287/orsc.1100.0580]
BURKE, P. J. (2006). 'Interaction in small groups.' In J. Delamater (Ed.), Handbook of Social Psychology (pp. 363–387). Berlin, Heidelberg: Springer.
BURT, R. S. (1982). Toward a Structural Theory of Action: Network Models of Social Structure, Perception and Action. Cambridge, MA: Academic Press.
CARLEY, K. M., & Hill, V. (2001). Structural change and learning within organizations. In A. Lomi & E. R. Larsen (Eds.), Dynamics of Organizations: Computational Modeling and Organizational Theories (pp. 63–92). Cambridge, MA: The MIT Press.
COHEN, M. D., March, J. G., & Olsen, J. P. (1972). A garbage can model of organizational choice. Administrative Science Quarterly, 17(1), 1–25. [doi:10.2307/2392088]
COLEMAN, J. S. (1973). Loss of power. American Sociological Review, 38(1), 1–17.
CONNOR, R. A., & Fiske, S. T. (2018). 'Warmth and competence: A feminist look at power and negotiation.' In C. B. Travis, J. W. White, A. Rutherford, W. S. Williams, S. L. Cook, & K. F. Wyche (Eds.), APA Handbook of the Psychology of Women: History, Theory and Battlegrounds (pp. 321–342). Washington, DC: American Psychological Association. [doi:10.1037/0000059-016]
CONNOR, R. C., Heithaus, M. R., & Barre, L. M. (2001). Complex social structure, alliance stability and mating access in a bottlenose dolphin "super-alliance". Proceedings of the Royal Society B: Biological Sciences, 268(1464), 263–267. [doi:10.1098/rspb.2000.1357]
COOK, K. S., & Emerson, R. M. (1978). Power, equity and commitment in exchange networks. American Sociological Review, 43(5), 721–739. [doi:10.2307/2094546]
CORRELL, S. J., & Ridgeway, C. L. (2006). 'Expectation states theory.' In J. Delamater (Ed.), Handbook of Social Psychology (pp. 29–51). Berlin, Heidelberg: Springer. [doi:10.1007/0-387-36921-x_2]
CORSARO, W. A., & Molinari, L. (2005). I compagni: Understanding Children’s Transition from Preschool to Elementary School. New York, NY: Teachers College Press.
DECKER, K. (1996). TAEMS: A framework for environment centered analysis & design of coordination mechanisms. Foundations of Distributed Artificial Intelligence, 429–448.
DONALD, M. (1991). Origins of the Modern Mind: Three Stages in the Evolution of Culture and Cognition. Cambridge, MA: Harvard University Press.
DUNBAR, R. I. M. (2009). The social brain hypothesis and its implications for social evolution. Annals of Human Biology, 36(5), 562–572. [doi:10.1080/03014460902960289]
ECKHARDT, E., Kaats, E., Jansen, S., & Alves, C. (2014). The merits of a meritocracy in open source software ecosystems. ACM International Conference Proceeding Series. [doi:10.1145/2642803.2642810]
FARARO, T. J., & Skvoretz, J. (1986). E-State Structuralism: A theoretical method. American Sociological Review, 51(5), 591–602. [doi:10.2307/2095486]
FISKE, S. T., & Stevens, L. E. (1993). 'What’s so special about sex? Gender stereotyping and discrimination.' In S. Oskamp & M. Costanzo (Eds.), Gender Issues in Contemporary Society (pp. 173–196). Thousand Oaks, CA: Sage Publications.
FLACHE, A., & Macy, M. (2011). 'Social dynamics from the bottom up: Agent-Based models of social interaction.' In P. Bearman & P. Hedström (Eds.), The Oxford Handbook of Analytical Sociology (pp. 245–268). Oxford, UK: Oxford University Press. [doi:10.1093/oxfordhb/9780199215362.013.11]
FREEMAN, L. C. (1978). Centrality in social networks conceptual clarification. Social Networks, 1(3), 215–239. [doi:10.1016/0378-8733(78)90021-7]
FRIEDKIN, N. E. (1991). Theoretical foundations for centrality measures. American Journal of Sociology, 96(6), 1478–1504. [doi:10.1086/229694]
GOFFMAN, E. (1959). The Presentation of Self in Everyday Life. London, UK: Harmondsworth.
GOLLOB, H. F. (1974). The subject-verb-object approach to social cognition. Psychological Review, 81(4), 286. [doi:10.1037/h0036591]
GRIMM, V., Railsback, S. F., Vincenot, C. E., Berger, U., Gallagher, C., DeAngelis, D. L., Edmonds, B., Ge, J., Giske, J., Groeneveld, J., Johnston, A. S. A., Milles, A., Nabe-Nielsen, J., Polhill, J. G., Radchuk, V., Rohwäder, M.-S., Stillman, R. A., Thiele, J. C., & Ayllón, D. (2020). The ODD protocol for describing agent-Based and other simulation models: A second update to improve clarity, replication, and structural realism. Journal of Artificial Societies and Social Simulation, 23(2), 7: https://www.jasss.org/23/2/7.html>. [doi:10.18564/jasss.4259]
GROW, A., & Flache, A. (2019). 'Agent-based computational models of reputation and status dynamics.' In F. Giardini & R. Wittek (Eds.), The Oxford Handbook of Gossip and Reputation (p. 230). Oxford, UK: Oxford University Press. [doi:10.1093/oxfordhb/9780190494087.013.13]
HEISE, D. R. (2007). Expressive Order: Confirming Sentiments in Social Actions. Berlin, Heidelberg: Springer Science & Business Media.
HEISE, D. R. (2010). 'Measurement reliability.' In D. R. Heise (Ed.), Surveying Cultures: Discovering Shared Conceptions and Sentiments (pp. 183–202). Hoboken, NJ: Wiley.
HEISE, D. R. (2013). Modeling interactions in small groups. Social Psychology Quarterly, 76(1), 52–72. [doi:10.1177/0190272512467654]
HOBAITER, C., Poisot, T., Zuberbüler, K., Hoppitt, W., & Gruber, T. (2014). Social network analysis shows direct evidence for social transmission of tool use in wild chimpanzees. PLoS Biology, 12(9), e1001960. [doi:10.1371/journal.pbio.1001960]
HOEY, J., MacKinnon, N. J., & Schröder, T. (2021). Denotative and connotative management of uncertainty: A computational dual-process model. Judgment and Decision Making, 16, 505–550.
HUBBELL, C. H. (1965). An input-Output approach to clique identification. Sociometry, 28(4), 377. [doi:10.2307/2785990]
KAPPELER, P. M. (1999). 'Convergence and divergence in primate social systems.' In J. G. Fleagle (Ed.), Primate Communities (pp. 158–170). Cambridge, MA: Cambridge University Press. [doi:10.1017/cbo9780511542381.010]
KATZ, N., Lazer, D., Arrow, H., & Contractor, N. (2004). Network theory and small groups. Small Group Research, 35(3), 307–332. [doi:10.1177/1046496404264941]
LAWLER, E. J., Thye, S. R., & Yoon, J. (2000). Emotion and group cohesion in productive exchange. American Journal of Sociology, 106(3), 616–657. [doi:10.1086/318965]
LINDENBERG, S. (1997). Grounding groups in theory: Functional, cognitive, and structural interdependencies. Advances in Group Processes, 14, 281–331.
LINDENBERG, S. (2015). 'Sociology of groups.' In J. D. Wright (Ed.), International Encyclopedia of the Social & Behavioral Sciences (pp. 434–440). Amsterdam, NL: Elsevier. [doi:10.1016/b978-0-08-097086-8.32064-5]
LYNN, F. B., Podolny, J. M., & Tao, L. (2009). A sociological (De)construction of the relationship between status and quality. American Journal of Sociology, 115(3), 755–804. [doi:10.1086/603537]
MARK, N. P., Smith-Lovin, L., & Ridgeway, C. L. (2009). Why do nominal characteristics acquire status value? A minimal explanation for status construction. American Journal of Sociology, 115(3), 832–862. [doi:10.1086/606142]
MARKOVSKY, B., & Lawler, E. J. (1994). A new theory of group solidarity. Available at: https://ecommons.cornell.edu/handle/1813/74893.
MARKOVSKY, B., Skvoretz, J., Willer, D., Lovaglia, M. J., & Erger, J. (1993). The seeds of weak power: An extension of network exchange theory. American Sociological Review, 58(2), 197. [doi:10.2307/2095966]
MASAD, D., & Kazil, J. (2015). Mesa: An agent-Based modeling framework. Available at: https://mesa.readthedocs.io/en/stable/. [doi:10.25080/majora-7b98e3ed-009]
MERTON, R. K. (1957). The role-Set: Problems in sociological theory. The British Journal of Sociology, 8(2), 106–120. [doi:10.2307/587363]
MERTON, R. K. (1968). Social Theory and Social Structure. New York, NY: Simon & Schuster.
MOLM, L. D., Peterson, G., & Takahashi, N. (1999). Power in negotiated and reciprocal exchange. American Sociological Review, 64(6), 876–890. [doi:10.2307/2657408]
MORGAN, J. H., Rogers, K. B., & Hu, M. (2016). Distinguishing normative processes from noise: A comparison of four approaches to modeling impressions of social events. Social Psychology Quarterly, 79(4), 311–332. [doi:10.1177/0190272516666794]
MOSS-RACUSIN, C. A., Phelan, J. E., & Rudman, L. A. (2010). When men break the gender rules: Status incongruity and backlash against modest men. Psychology of Men & Masculinity, 11(2), 140–151. [doi:10.1037/a0018093]
OSGOOD, C. E., May, W. H., & Miron, M. S. (1975). Cross-Cultural Universals of Affective Meaning. Champaign, IL: University of Illinois Press.
OWENS, T. J., Robinson, D. T., & Smith-Lovin, L. (2010). Three faces of identity. Annual Review of Sociology, 36, 477–499. [doi:10.1146/annurev.soc.34.040507.134725]
PIAGET, J. (1977). 'Problems of equilibration.' In M. Appel (Ed.), Topics in Cognitive Development (pp. 3–13). Berlin Heidelberg: Springer. [doi:10.1007/978-1-4613-4175-8_1]
POWERS, W. T. (1973). Behavior: The Control of Perception. Chicago, IL: Aldine Transaction.
PRIETULA, M. J., & Carley, K. M. (1994). Computational organization theory: Autonomous agents and emergent behavior. Journal of Organizational Computing and Electronic Commerce, 4(1), 41–83. [doi:10.1080/10919399409540216]
RIDGEWAY, C. (1991). The social construction of status value: Gender and other nominal characteristics. Social Forces, 70(2), 367–386. [doi:10.2307/2580244]
RIDGEWAY, C. L. (2019). Status: Why Is It Everywhere? Why Does It Matter? New York, NY: Russell Sage Foundation.
RIDGEWAY, C. L., & Bourg, C. (2004). 'Gender as status: An expectation states theory approach.' In A. H. Eagly, A. E. Beall, & R. J. Sternberg (Eds.), The Psychology of Gender (pp. 217–241). Guilford, Surrey: The Guilford Press.
RIDGEWAY, C. L., & Smith-Lovin, L. (1999). The gender system and interactions. Annual Review of Sociology, 25, 191–216. [doi:10.1146/annurev.soc.25.1.191]
RUDMAN, L. A. (1998). Self-Promotion as a risk factor for women. Journal of Personality and Social Psychology, 74(3), 629–645. [doi:10.1037/0022-3514.74.3.629]
SCACCHI, W. (2007). Free/open source software development: Recent research results and emerging opportunities. ESEC/FSE’07: 6th Joint Meeting of the European Software Engineering Conference and the ACMSIGSOFT Symposium on the Foundations of Software Engineering - Companion Papers [doi:10.1145/1295014.1295019]
SCHAUENBURG, G., Conrad, M., von Scheve, C., Barber, H. A., Ambrasat, J., Aryani, A., & Schröder, T. (2019). Making sense of social interaction: Emotional coherence drives semantic integration as assessed by event-related potentials. Neuropsychologia, 125, 1–13. [doi:10.1016/j.neuropsychologia.2019.01.002]
SCHRÖDER, T., Hoey, J., & Rogers, K. B. (2016). Modeling dynamic identities and uncertainty in social interactions: Bayesian affect control theory. American Sociological Review, 81(4), 828–855.
SCHRÖDER, T., & Scholl, W. (2009). Affective dynamics of leadership: An experimental test of affect control theory. Social Psychology Quarterly, 72, 180–197. [doi:10.1177/019027250907200207]
SKVORETZ, J., Faust, K., & Fararo, T. J. (1996). Social structure, networks, and E-state structuralism models. Journal of Mathematical Sociology, 21(1–2), 57–76. [doi:10.1080/0022250x.1996.9990174]
SMITH-LOVIN, L., & Heise, D. R. (2006). Mean affective ratings of 2,106 concepts by University of North Carolina undergraduates in 1978. Data in Computer Program Interact, 25, 2012.
STRODTBECK, F. L., & Mann, R. D. (1956). Sex role differentiation in jury deliberations. Sociometry, 19(1), 3. [doi:10.2307/2786099]
TERRELL, J., Kofink, A., Middleton, J., Rainear, C., Murphy-Hill, E., Parnin, C., & Stallings, J. (2017). Gender differences and bias in open source: Pull request acceptance of women versus men. PeerJ Computer Science, 2017(5), 1–25. [doi:10.7717/peerj-cs.111]
THAGARD, P. (2001). 'How to make decisions: Coherence, emotion, and practical inference.' In E. Millgram (Ed.), Varieties of Practical Inference (pp. 355–371). Cambridge, MA: The MIT Press.
VEDRES, B., & Vasarhelyi, O. (2019). Gendered behavior as a disadvantage in open source software development. EPJ Data Science, 8(25), 2019. [doi:10.1140/epjds/s13688-019-0202-z]
WOOLLEY, A. W., Aggarwal, I., & Malone, T. W. (2015). Collective intelligence and group performance. Current Directions in Psychological Science, 24(6), 420–424. [doi:10.1177/0963721415599543]
ZÖLLER, N., Morgan, J. H., & Schröder, T. (2020). A topology of groups: What GitHub can tell us about online collaboration. Technological Forecasting and Social Change, 161, 120291.