An Agent-Based Model of MySide Bias in Scientific Debates

, , , , ,
and
aLAMSADE, Université Paris-Dauphine, France; bRuhr University Bochum, Germany; cPhilosophy and Ethics Group, Technical University of Eindhoven, Netherlands; dUtrecht University, Netherlands
Journal of Artificial
Societies and Social Simulation 27 (3) 1
<https://www.jasss.org/27/3/1.html>
DOI: 10.18564/jasss.5413
Received: 16-Oct-2023 Accepted: 11-Apr-2024 Published: 30-Jun-2024
Abstract
In this paper, we present an agent-based model for studying the impact of 'myside bias' on the argumentative dynamics in scientific communities. Recent insights in cognitive science suggest that scientific reasoning is influenced by `myside bias'. This bias manifests as a tendency to prioritize the search and generation of arguments that support one's views rather than arguments that undermine them. Additionally, individuals tend to apply more critical scrutiny to opposing stances than to their own. Although myside bias may pull individual scientists away from the truth, its effects on communities of reasoners remain unclear. The aim of our model is two-fold: first, to study the argumentative dynamics generated by myside bias, and second, to explore which mechanisms may act as a mitigating factor against its pernicious effects. Our results indicate that biased communities are epistemically less successful than non-biased ones, and that they also tend to be less polarized than non-biased ones. Moreover, we find that two socio-epistemic mechanisms help communities to mitigate the effect of the bias: the presence of a common filter on weak arguments, which can be interpreted as shared beliefs, and an equal distribution of agents for each alternative at the beginning.Introduction
The process of scientific inquiry has long intrigued social scientists and philosophers of science. How can individual scientists, driven by various incentives, jointly form a community that effectively and efficiently achieves its epistemic goals? Inspired by formal approaches in economics, the late '90s gave rise to various analytical models examining the relationship between individual and group rationality (e.g., Kitcher 1990; Brock & Durlauf 1999; Zamora Bonilla 1999). Soon after, with the introduction of computational methods more complex scenarios have been investigated. In particular, simulations in the form of agent-based models (ABMs) were introduced to study how local interactions among individual scientists bring about emergent phenomena characterizing collective inquiry (e.g., Gilbert 1997; Hegselmann & Krause 2006; Zollman 2007).
While various ABMs were developed to study the process of scientific interaction, the argumentative aspect of scientific deliberation has only recently gained attention in this body of literature. This is surprising given that argumentation has traditionally been considered of central importance for the progress of science (Kuhn 2000; Pera 1994; Popper 1962; Rescher 2007), and the idea that knowledge production relies on a continuous scientific debate, in which arguments are criticized, rejected or defended, is widely recognized as the cornerstone of scientific objectivity (Douglas 2009). In fact, although individual scientists may suffer from various biases, the continuous critical exchange is meant to keep these biases in check (Longino 2002). At the same time, we lack a precise understanding of mechanisms that allow a scientific community to achieve its goals despite the pervasive presence of biases (Zollman 2011).
This paper aims to examine one such bias which has gained significant attention in cognitive science: what Mercier, Sperber and colleagues define as myside bias (Mercier 2017). They argue that reasoning is inherently argumentative, and rather than being focused on tracking truth, it fulfills two argumentative functions: to convince an audience and to evaluate the arguments of other agents (Mercier 2017; Mercier & Sperber 2017). In their view, myside bias concerns the first function, where reasoning operates in a biased way by predominantly producing arguments in favour of held views rather than seeking out defeating arguments. We stick here to the conceptalisation by Mercier, Sperber and colleagues (Mercier et al. 2016; Mercier & Heintz 2014; Mercier & Sperber 2011) that only consider myside bias as a production bias, and differentiate from other uses of the notion, concerned either only with the evaluation of arguments or with both production and evaluation (Baron 1995; Mercier 2017; Stanovich et al. 2013; Stanovich & West 2007; Wolfe & Britt 2008).1 The characterization of myside bias in terms of the production of reasons renders myside bias essentially part of argumentative reasoning. As such, it affects various reasoning contexts, including scientific reasoning (Mercier & Heintz 2014).
While myside bias may pull scientists away from the truth, the effect is most disastrous when scientists reason isolated from a social context. As soon as agents exchange arguments, argument evaluation takes place, where reasoning is “quite good at telling apart good from bad arguments” (p. 516). Therefore, Mercier & Heintz (2014) conjecture that the detrimental effects may be absorbed in the social context of a scientific community in which pro and con arguments are exchanged and critically evaluated.
Moreover, potential adverse effects of myside bias can be further mitigated when scientists share evaluative standards for what counts as a good argument (Mercier & Heintz 2014). Shared evaluative standards consist of shared “beliefs about what a good argument looks like” (ibid, p. 519), which enable agents of a community to weed out weak arguments. As Mercier & Heintz (2014) argue, different scientific domains come with more or less such shared standards. While mathematics comes with a rather strict regiment of what counts as a proof, we see more variety and dynamics in other disciplines such as psychology, where in response to the replication crisis new standards obtain increasing significance (such as preregistered studies, etc.). Mercier and Heintz look at these shared beliefs as a possible tool for scientific community to contrast the effect of bias, insofar as they help weeding out poor arguments.
This view contrasts sharply with a more traditional take on confirmation bias as generally epistemically pernicious. At the same time, it coheres with recent proposals that confirmation bias, while harmful for an isolated reasoner, may not be detrimental to group inquiry (Peters 2020; Smart 2018). Therefore, the current state of the art raises the question: How exactly does myside bias impact collective inquiry?
We aim to address this issue. In particular, we will examine two closely related questions:
- Q1: What kind of effect (if any) does the bias create in a scientific community that exchanges arguments?
- Q2: Do shared beliefs in the form of shared evaluative standards among scientists help to mitigate the detrimental effects of the bias?
Answering these questions is crucial to better understand the impact of myside bias on scientific debates and collective inquiry in general.
To investigate these issues, we develop an ABM2 based on the abstract argumentation framework (Dung 1995). Abstract argumentation has previously been used for the formal modeling of scientific debates (Šešelja & Straßer 2013) as well as in agent-based modeling of scientific inquiry (Borg et al. 2019, 2018). At the same time, applications of abstract argumentation to the study of biases, and the phenomenon of myside bias in particular, have been lacking. Modeling a scientific debate in terms of abstract argumentation allows us to represent myside bias in line with Mercier and Sperber’s view: as a cognitive mechanism that affects the production of arguments. In addition, it also allows us to test whether the presence of shared evaluative standards (Mercier & Heintz 2014) acts as a mitigating factor against the insidious effects of the bias.
The paper is structured as follows. Section 2 provides the necessary background by introducing myside-bias in more detail and our choice of argumentation framework underpinning our model. In Section 3, we present our model. and in Section 4, the central results of the simulations. In Section 5, we compare our contribution with other formal models that have addressed similar questions. Section 6 concludes the paper.
Myside Bias and Scientific Argumentation
Myside bias affects the production of arguments of scientists, and our research questions Q1 and Q2 concern its effects on scientific inquiry. Given the complexity underlying scientific argumentative exchange, we propose to investigate these questions with an agent-based model that represents the argument exchange through abstract argumentation (Dung 1995). This section motivates our choice.
Myside bias as a production bias
Mercier, Sperber and colleagues consider myside bias as an individual bias that affects the way arguments are produced. Yet, because of the extreme complexity of the scientific debate, the way such a bias impacts the epistemic performance of a scientific community cannot easily be derived in the absence of a clear formalization of the way agents interact. To see this consider a concrete example.
Example 1. In the first half of the twentieth century, the earth scientist Alfred Wegener proposed the continental drift hypothesis, which postulated that continents used to be connected and had subsequently drifted apart to their current locations. Wegener’s theory (‘Drift’) conflicted with two other theories endorsed by earth scientists at the time: ‘Contractionism’, according to which the phenomena on the surface of the Earth are explained by the Earth’s gradual cooling and contracting, and ‘Permanentism’, which postulated that no major lateral shifts occurred on the Earth’s surface (Šešelja & Straßer 2013; Šešelja & Weber 2012). Wegener’s theory offered a unifying explanation of various phenomena – from the jigsaw-like fit of the continental coastlines to the similarity between flora and fauna on the opposite sides of the ocean. However, it suffered from a major conceptual issue: the lack of a plausible mechanism of the Drift, explaining how continents could move through (what appeared to be) the hard ocean floor.
Suppose now that scientists involved in such a debate were affected by myside bias. How could have the myside bias influenced the debate? From the individual perspective, the bias make agents more likely to produce arguments in favour of their own theory than arguments critical of it, and more likely to make arguments critical of rival theories than arguments that would support them (Mercier 2017; Mercier & Sperber 2017). In the drift debate, this may have resulted in ‘biased drifters’ who were more likely to produce arguments in favour of the explanatory power of Drift than arguments elaborating on the lack of a plausible mechanism of drifting continents. In contrast, ‘biased contractionists’ may have been more likely to produce the latter kind of arguments than those concerning problems within their own theory (such as the presence of radioactive materials in the Earth, which indicated the Earth could be heating up rather than cooling down).
However, our intuitions let us down when it comes to envisioning how the bias affected the collective debate. Supposing agents were biased, did the bias actually delay the production of important arguments? Or perhaps its presence had little to no influence given that it was equally distributed across the proponents of all the competing theories? Did the fact that ‘drifters’ were a minority in the community modified the collective impact of bias?
Abstract argumentation and ABMs are the ideal tools to model how myside bias affects a debate. Abstract argumentation has previously been used for the formal modeling of scientific debates (Šešelja & Straßer 2013) as well as in agent-based modeling of scientific inquiry (Borg et al. 2019, 2018). It provides a precise and schematic representation of the evolution of a debate. Agent-based modeling enables the study of the collective outcome starting from the individual interactions.
Although argumentation and various forms of biased reasoning have been studied through ABMs, no ABM, to our knowledge, has focused on the combination of argumentation and myside bias intended as a production bias. On the one hand, ABMs studying argumentative dynamics have mainly focused on the argumentative exchange as free from the intrusion of cognitive biases (e.g., Mäs & Flache 2013; Borget al. 2017b; Kopecky 2022; Taillandier et al. 2021). On the other hand, ABMs studying the impact of confirmation bias on the scientific inquiry have tackled this issue independently of argumentation (Baccini et al. 2023; Baccini & Hartmann 2022; Gabriel & O’Connor 2024). Confirmation bias is here considered as impacting the evaluation of one’s beliefs (e.g, by discounting opposing evidence) rather than affecting the production of one’s arguments. Similarly, ABMs studying how biases affect argumentative exchange have focused on evaluative aspects of biased reasoning, and on broader contexts of deliberation, not aimed at inquiry and scientific goals in particular (Banisch & Shamon 2023; Dupuis de Tarlé et al. 2022; Proietti & Chiarella 2023; Singer et al. 2018).
Now, before proceeding to the presentation of our model (in Section 3.1), we introduce the framework of abstract argumentation. We do so by providing some useful notions and an illustrative example of how abstract argumentation may model the debate of Example 1.
Abstract argumentation
To simulate a biased production of arguments in a community of deliberating agents, we first need a suitable modeling framework. A particularly suitable framework for the formal study of argumentation is abstract argumentation. Originally developed in symbolic AI (Dung 1995), abstract argumentation has been increasingly used for agent-based modeling of deliberating communities (e.g., Gabbriellini & Torroni 2014; Borget al. 2017a; Butler et al. 2019; Dupuis de Tarlé et al. 2022; Taillandier et al. 2021).
Formally, an abstract argumentation framework (AF) is a directed graph in which the nodes are abstract representations of arguments and edges represent argumentative attacks. In this way, AFs can be used to model a stance of a rational reasoner in a debate: by assigning to each agent a specific argumentation graph we can represent a set of arguments and attacks between them, forming the agent’s argumentation map. Moreover, we can define the rules specifying which arguments are acceptable, or which arguments should be rejected.
Given an AF, Dung defined different ways in which sets of arguments can be deemed acceptable in a given argumentation framework. These sets intuitively characterize rational positions in a debate. In this paper we use the grounded set due to its uniqueness.3
The following example illustrates how abstract argumentation models a scientific discussion.
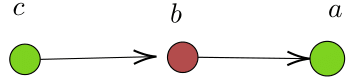
Example 2. Imagine how a stylized dicussion between Alfred Wegener, proponent of ‘Drift’, and Ernest Ingersoll, proponent of ‘Permanentism’, may have played out (see Example 1). Wegener could have stated argument \(a\): ‘since the continents look like a jigsaw puzzle, they must have drifted away from each other’. Ingersoll could have pointed out that ‘although they may look as a jigsaw puzzle from a distance, their borders do not really match’ (argument \(b\)). Finally, Wegener could have rebutted Ingersoll’s argument by suggesting that ‘the differences must have been caused by erosion’, which would constitute argument \(c\). The argumentation graph capturing this debate is illustrated in Figure 1. While \(b\) attacks \(a\), \(c\) attacks \(b\) and thus defends \(a\). Given this stage of the debate, we can say that a set of arguments \(S=\{a,c\}\) is grounded and acceptable.
As the example illustrates, the argumentation map of a reasoner may grow indefinitely, with new counterarguments being added to the graph.
The Model
In this section, we introduce our model. We start by describing how agents evaluate a debate and update their preferences. This will help us to define the general setting of our simulations. Subsequently, we lay out our model’s protocol, starting with the baseline case, and only after introducing the modelling of myside bias. Finally, we detail the metrics we use to measure a community’s epistemic success and polarisation.
Modelling opposing views with argumentation frameworks
Our model represents a scientific community whose members try to decide between two competing alternative research programmes. In the context of science, they could be, for example, competing scientific theories or explanations. Informally speaking, a research programme is constituted by a certain number of claims.
We call the arguments included in a research programme central arguments (hence, \(N_{\textit{CA}}\) is the number of central arguments per program). Central arguments provide the central theoretical tenets of a research programme. They give the argumentative support to the core hypothesis of the program. For example, in the continental drift research programme by Wegener, some of the central arguments were: (a) Jigsaw fit of the continental coastlines, indicating that the continents were once connected; (b) Similarity of flora and fauna on the opposite sides of the ocean, indicating that the biological systems on different continents were once united; etc. Both research programmes contain the same number of distinct central arguments.
Agents engage in a debate by discussing the central arguments of two opposing research programmes, \(\mathit{ResProg}_1\) and \(\mathit{ResProg}_2\). For this, they produce additional (dialetical) arguments that are not contained in research programmes and which are used to attack and/or defend central arguments. For example, the argument concerned with the similarity of flora and fauna can be attacked by claiming that such similarity is the result of the adaptation to similar climate and geological circumstances, and not of the fact that continents were once united.
Each agent \(i\) has her own view of the debate at time \(t\). The view of an agent determines what agent \(i\) thinks is the state of the art regarding the discussion between \(\mathit{ResProg}_1\) and \(\mathit{ResProg}_2\) at time \(t\).
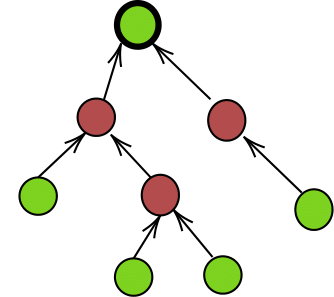
As such, the view of an agent always contains the central arguments of each research programme, and may then include new arguments that are relevant to the debate. Arguments may be connected by attack relations. An attack relation from an argument \(x\) to an argument \(y\) represents an explicit argumentative move that challenges argument \(y\). Such an argumentative move may be obtained through empirically refuting one important step of the attacked argument, by pointing out a methodological mistake and so on. As a simplification, no attack relation is present among the central arguments given their supportive character.4 Because of how views are built (see Section "Baseline protocol"), they have two special features. First, each central argument of a research programme is the root of an in-tree, that is a tree where all edges point towards the root. Second, each argument \(a \in \mathcal{A}_i\) belongs to one and only one of the in-trees that can be found in the framework, that is every non-central argument can be linked by a path with one and only one of the central arguments. Figure 2 presents an example of an in-tree with its own root, and Figure 3 presents an example of a view. While the view of every agent contains the central arguments of each research programme, different agents can have different views.
Based on her own view of the debate, an agent assigns a score to each research programme, by applying the acceptability semantics. The score of a research programme is equal to the number of its central arguments that are acceptable in her view.
| \[\mathit{score}_i^t(\mathit{ResProg}_j) = |\{a \in ResProg_j | a \textit{ is acceptable in } V_i^t\}|.\] | \[(1)\] |
Whenever one of the two research programme has a higher score than the other one for an agent \(i\), we say that agent \(i\) prefers it. When agents have different views, they may assign different scores to the same research programmes, and, consequently, have different preferences for research programmes.
Finally, we introduce a function \(S\), which assigns a dialectic strength to each argument, in short strength. Whenever an agent looks for a counterargument to \(a\), the probability with which such an attack is generated depends on the strength of \(a\), that is \(S(a)\). The variability in argument strength accounts for the intuitive observation that some arguments are more convincing and harder to attack than others. We assume that the central arguments of a research programme have the same strength. This modeling choice allows us to decide which (if any) of the two research programmes is objectively stronger and, consequently, objectively preferable. A more robust research programme represents a research programme that is based on stronger evidence or provides better explanations than the rival one.
We call \(S_1\) and \(S_2\), respectively, the values for the strength of the central arguments in \(\mathit{ResProg}_1\) and in \(\mathit{ResProg}_2\), i.e., if \(a\) is a central argument of \(\mathit{ResProg}_1\), \(S(a) = S_1\). Section "Baseline protocol" explains how the value \(S(a)\) is computed if \(a\) is not a central argument. We refer from now on to \(S_i\) interchangeably as either ‘the strength of \(\mathit{ResProg}_i\)’ or as ‘the strength of the central arguments of \(\mathit{ResProg}_i\)’. The strengths of the two research programmes \(S_1, S_2\) are treated as simulation parameters.5
Our model simulates an ongoing debate among scientists about the merits of two research programmes \(\mathit{ResProg}_1\) and \(\mathit{ResProg}_2\). It does so through a succession of \(T\) steps in which agents generate new argumentative attacks and update their views and preferences for research programmes. One could think of arguments in terms of the argumentative content of research papers published by scientists within a certain debate. We begin by outlining the baseline protocol, and then proceed to the following two subsections, where we describe the implementation of myside bias and a specific mechanism aimed at mitigating its harmful impact.
Baseline protocol
Initialization. Each agent \(i\) is initialized with a view whose argument set contains only the central arguments of both research programmes and no attack relation, i.e., \(V_i^0 = \langle \mathcal{A}_i^0, \mathcal{R}_i^0 \rangle\) such that \(\mathcal{A}_i^0 = ResProg_1 \cup ResProg_2\) and \(\mathcal{A}_i^0 = \emptyset\) (see Figure 4 for an example). Since all agents have access to the same set of arguments, their views are identical at the start of the simulation and cannot be used to determine their preferences. The preference of each agent at step \(0\) is defined by parameter \(n^0_1\) (called initial support), which specifies the number of agents who prefer \(\mathit{ResProg}_1\). All of the remaining agents prefer \(\mathit{ResProg}_2\).
Protocol. Each step has three phases.
Phase 1: “Attack generation”.
- Each agent \(i\) randomly chooses some argument \(a\) among those present in her set of arguments \(\mathcal{A}_i^t\).
- Each agent \(i\) tries to generate a counterargument to \(a\), that is, a new attacker \(b\) of \(a\). The success rate of generating the counterargument is \(p_{\it attack} = 1 - S({a})\) where \(S({a})\) is the strength of \(a\). If successful, the new argument \(b\) obtains a strength \(S({b})\) drawn from a normal distribution centered on \(1- S({a})\) with standard deviation \(\mathit{StDev}\). The argument generation probability \(p_{\it attack}\) is based on the idea that attacking weak arguments is easier than attacking strong ones. The strength generation is based on the idea that attackers of strong arguments will be on average weaker, and vice versa.6
- For each generated argument \(b\), the community decides whether it should be considered. The default assumption is that the community considers all the generated arguments, unless it employs specific mechanisms for their filtering (we will introduce one such mechanism in Section 3.21).
- The agent \(i\) who produced argument \(b\) always adds argument \(b\) and the correspondent attack relation \((b, a)\) to her view (regardless of whether the community has filtered that argument). If the community decides the argument \(b\) should be considered, each other agent may include it or not in her view. Every agent \(j\) who does not know argument \(a\), that is \(a \notin \mathcal{A}_j\), does not add argument \(b\) nor relation \((b, a)\) to her view. Finally, an agent \(k\) who knows \(a\) but did not produce \(b\) adds the argument \(b\) and the relation \((b, a)\) to her view with probability \(p_{\it see}\).
- Each agent \(i\) computes the score for each research programme based on her view (Definition 7) and updates her preference accordingly. She prefers the \(\mathit{ResProg}\) with the highest score, and does not change her opinion if the two programs are equal.
Through this protocol, the views of the agents are populated. In the beginning the only arguments the agents know are the central arguments of each research programme, and a new argument can only attack an argument that is already present. As a consequence, each central argument of a research programme is the root of an in-tree, that is a tree where all edges point towards the root, and no cycle can be formed (similarly to Borg et al. 2018; Proietti & Chiarella 2023). This reflects the unfolding of a scientific debate, in which the new arguments produced are usually unlikely to be attacked by arguments that are already present. Notably, if the probability of including an argument for the agents in the community is lower than 1 (\(p_{\it see} < 1\)), the agents will have distinct views which will not contain every argument that has been produced.
Our agents evaluate the debate impartially, insofar as they always support the research programme with the highest score. As mentioned, the score of a program corresponds to the number of its central arguments that are acceptable. As such, it indicates the strength of a program given the present state of the debate: the program with the higher score is the one that appears as the stronger one.
Example 3. Let us illustrate this protocol with the first step of a debate concerning two research programmes of strength \(S_1 = 0.5\) and \(S_2=0.8\). Each research programme contains two central arguments, as shown in Figure 4: arguments \(a\) and \(b\) for \(\mathit{ResProg}_1\) and \(c\) and \(d\) for \(\mathit{ResProg}_2\). For the sake of simplicity, we consider the view of only a single agent \(\mathit{Agent}_1\) who begins the simulation with a preference for \(\mathit{ResProg}_1\). Her view at time \(t = 0\) (\(V_1^0\)) is shown in Figure 4.
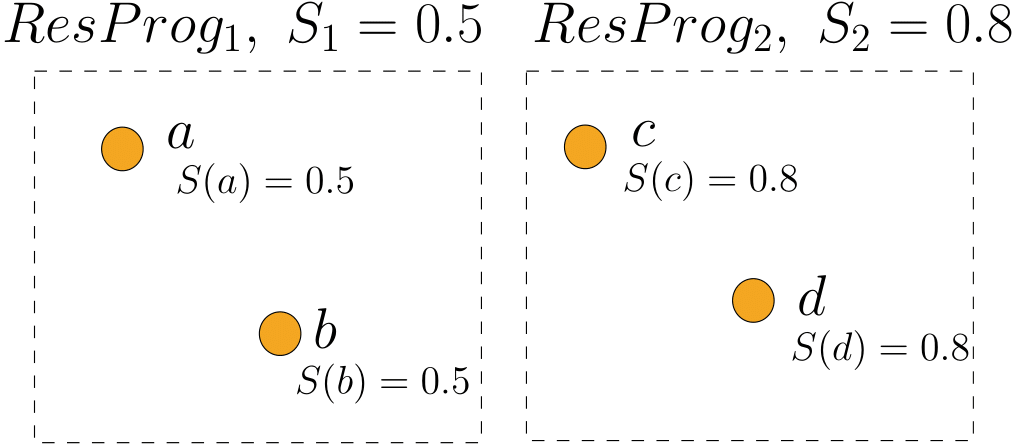
First, \(\mathit{Agent}_1\) randomly selects an argument from her view (\(V_1^0\)), in this case \(a\). The agent tries to generate an attacking argument with a probability \(p_{\it attack} = 1 - S(a) = 0.5\). The agent succeeds: a new argument \(e\) that attacks \(a\) is created. The strength of \(e\) is sampled from a normal distribution of mean \(1- S(a) = 0.5\). We obtain a strength of \(0.43\) (\(S(e) = 0.43\)). The view at time \(t = 1\) (\(V_1^1\)) shown in Figure 5 is the result of updating the initial view by adding the new argument \(e\) and an attack between \(e\) and \(a\).
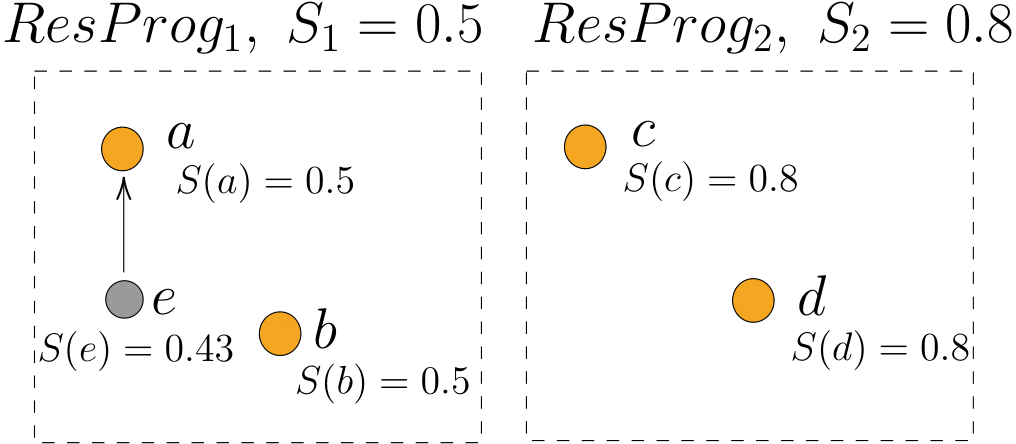
Then, \(\mathit{Agent}_1\) computes the score of each research programme by counting the number of acceptable central arguments in her view. Here, arguments \(b\), \(c\) and \(d\) are not attacked and are thus acceptable, while \(a\) is attacked but not defended which makes it not acceptable. The scores of each research programme for agent \(1\) are \(\mathit{score}(\mathit{ResProg}_1) = 1\) and \(\mathit{score}(\mathit{ResProg}_2) = 2\). Since \(\mathit{ResProg}_2\) has a higher score than \(\mathit{ResProg}_1\), \(\mathit{Agent}_1\) changes her preference to \(\mathit{ResProg}_2\) for the next step.
MySide bias in the production of arguments
As mentioned above, myside bias is modelled as a factor that makes it easier to produce arguments in favour of one’s standpoint. In our protocol, the bias increases the probability of generating a counterargument in case the counterargument will favour the agent’s preferred research programme. An argument favours one’s preferred research programme if it either defends the program or attacks the opposing one (recall Definition 3).
We model a biased community by changing the process of argument generation as follows. First, each agent is equipped with a bias parameter \(\mathit{bias}\in [0,1]\). If an agent is investigating an argument \(a\) in favour of her preferred research programme, then
| \[\begin{aligned} p_{attack} = \begin{cases} 1 - S(a) - \mathit{bias}&\text{ if } 1 - S(a) - \mathit{bias}\geq 0,\\ 0 &\text{ otherwise. } \end{cases} \end{aligned}\] | \[(2)\] |
| \[\begin{aligned} p_{attack} = \begin{cases} 1 - S(a) + \mathit{bias}&\text{ if } 1 - S(a) + \mathit{bias}\leq 1,\\ 1 &\text{ otherwise. } \end{cases} \end{aligned}\] | \[(3)\] |
The bias parameter changes the probability with which an agent finds a counterargument against a certain argument, based on the agent’s preference. The higher the parameter is, the more biased the agents are. When \(\mathit{bias}=0\) for all agents, we are in the baseline case of an unbiased community.
Example 4. To illustrate the difference induced by the bias, consider the first step of the same debate of Example 3, where \(\mathit{Agent}_1\) is now biased with \(\mathit{bias}=0.3\). The view of \(\mathit{Agent}_1\) is the same at the beginning (Figure 4), and she begins the simulation with a preference for \(\mathit{ResProg}_1\). \(\mathit{Agent}_1\) randomly selects an argument from \(V_1^0\), in this case \(a\). Attacking \(a\) would be against the agent’s preferred research programme, \(\mathit{ResProg}_1\). The agent tries to generate an attacking argument with a probability \(p_{\it attack} = \max(1 - S(a) - \mathit{bias}, 0) = 0.2\). The agent is more likely to fail than in the non-biased case. Let us assume that she fails to generate an attack towards \(a\). Her view does not change in the next step. \(\mathit{Agent}_1\) computes the score of each research programme by counting the number of acceptable central arguments in her view. Here, arguments \(a\), \(b\), \(c\) and \(d\) are not attacked and thus acceptable. The scores of the two research programmes for \(\mathit{Agent}_1\) are the same: \(\mathit{score}(\mathit{ResProg}_1) = 2\) and \(\mathit{score}(\mathit{ResProg}_2) = 2\). Since \(\mathit{score}(\mathit{ResProg}_1) = \mathit{score}(\mathit{ResProg}_2)\), agent \(1\) keeps preferring \(\mathit{ResProg}_1\) in the next round.
This example highlights how the bias makes it harder to generate arguments against one’s preferred research programme, even though the arguments one is trying to attack may be weak. As such, the bias may comfort the agents in their opinions, and be detrimental to their assessment of the best research programme. In this case, it is as though her bias prevents \(\mathit{Agent}_1\) from seeing the faults of her preferred point of view.
Recall that we assume biased agents to evaluate the debate and choose which program to support using the same procedure as non-biased agents. This is a crucial aspect of the account of myside bias by Mercier & Heintz (2014), who argue that myside bias does not affect the evaluation of arguments, but only their production. Our agents are biased when they generate arguments, not when they evaluate the research programmes.
Shared beliefs as shared standards of evaluation
Mercier & Heintz (2014) suggest that the presence of shared beliefs may help a community to perform better and exhibit reduced susceptibility to the harmful effects of myside bias. The idea is that the production of arguments is improved if agents can anticipate counter-arguments from other agents. This anticipation, in turn, is more effortless when agents share beliefs. When agents share beliefs, they anticipate counter-arguments more easily and, as a consequence, they do not publish arguments that their communities would immediately rebut. Indeed, by doing so an agent avoids the loss of reputation that would result of not being able to defend her own stance.
Therefore, shared beliefs may act as shared standards of evaluation, that is as a mechanism to weed out bad arguments from good arguments. By way of illustration, we can compare the social sciences with the natural sciences. The latter is characterized by a higher degree of shared beliefs than the former, and, consequently, agents are better at anticipating what the possible counter-arguments to their own arguments will be. This implies that the standards for arguments are clearer and sharper, and less weak arguments are published. In the context of science such standards are tracked by communal practices such as peer review.7
In our model, we investigate the role of shared beliefs insofar as they act as shared standards, that is as a filter that enables a community to reject arguments which are too weak. In this way weak arguments do not affect scientific discourse. That is, before a newly generated argument is added to individual views, it is decided whether it is worthy of consideration. If not, only the author adds the argument to her own view, while no other agent has the opportunity to integrate it into her view.
The probability for an argument \(a\) to be discarded depends on its strength \(S(a)\) and a fixed shared belief parameter \(\mathit{shBel}\in [0,1]\):
| \[p_{\it discard} = \mathit{shBel}\cdot (1 - S(a)).\] | \[(4)\] |
In this way our model implements a "slim version" of the mechanism of shared beliefs proposed by Mercier & Heintz. One that focuses on the collective effect of shared beliefs, while bracketing the individual processes (such as anticipations and reputation) of the agents. By doing so, we make sure to introduce in the model the kind of effect on argument production Mercier and Sperber had in mind, that is that of an epistemic collective filter.
Simulations and observation
In our simulation, a community of agents investigates two research programmes by producing new arguments. Each research programme has an objective strength, which corresponds to the strength of each of its central arguments. Although the agents do not know the strength of either of the programs, they aim at understanding which program is stronger by debating and arguing about the central arguments. In fact, the strength values of the central arguments affect the shape of the debate, insofar as stronger arguments are harder to attack, and usually easier to defend. By generating arguments, agents aim at eliciting which program is objectively stronger. In an epistemically ideal situation an objectively stronger research programme would always be the one with the highest score. Yet, this may not always be the case, e.g., when agents are biased.
Each scientist always supports the research programme that appears stronger to her, i.e., the one that has the highest score in her view. We hypothesize that in baseline conditions, the scores the scientists assign to the two programs will likely respect the respective strengths of the central arguments.
Now, we shall summarize the parameters of our simulation (see Table 1 for an overview). To do so, we formally define the community \(\mathit{Com}\) and environment \(\mathit{Env}\). A community \(\mathit{Com}\) describes all the socio-epistemic features of the collective that engages in the debate: its size (\(N\)), the initial support granted to \(\mathit{ResProg}_1\) (\(n_1^0\)), the strength of the bias (\(\mathit{bias}\)), and the strength of the shared beliefs (\(\mathit{shBel}\)). It is a quadruplet \(\mathit{Com}= \langle N, \mathit{bias}, \mathit{shBel}, n_1^0 \rangle\). An environment \(\mathit{Env}\) describes the conditions of the scientific controversy: the number of central arguments per research programme (\(N_{\textit{CA}}\)) and the coefficient that determines the standard deviation of the distribution from which the strength of a new argument is drawn (\(StDev\)). It is given by a pair \(\mathit{Env}= \langle N_{CA}, \mathit{StDev}\rangle\). Finally, there are the two research programmes, \(\mathit{ResProg}_1\) and \(\mathit{ResProg}_2\), that come with their respective strengths \(S_1, S_2\).
| Parameter | Definition | Test Interval | Default Value |
|---|---|---|---|
| \(N\) | Number of agents. | \([2, 12]\) | 10 |
| \(n_1^0\) | Initial support for \(\mathit{ResProg}_1\). | \([0, N]\) | 5 |
| \(N_{CA}\) | Number of central arguments in each research programme. | \([1, 10]\) | 5 |
| \(p_{\it see}\) | Probability for an agent to add an argument to her personal view. | \([0.5, 1]\) | 0.5 |
| \(\mathit{StDev}\) | Standard deviation of the probability distribution for the generation of argument strength. | \([0.1, 0.5]\) | 0.2 |
| \(\mathit{bias}\) | Bias parameter. | \([0,1]\) | 0.3 |
| \(\mathit{shBel}\) | Shared beliefs parameter. | \([0,1]\) | - |
| \(S_1\) | Strength of \(\mathit{ResProg}_1\). | \([0, 1]\) | - |
| \(S_2\) | Strength of \(\mathit{ResProg}_2\). | \([0, 1]\) | - |
Epistemic evaluation
We want to characterize the epistemic success of a community \(\mathit{Com}\) in a specific environment \(\mathit{Env}\). The idea is to measure how good the collective of agents is at selecting the best research programme for different values of the strengths of the research programmes (\(S_1, S_2\)).
To evaluate the performance of a community we start by defining two fundamental notions. First, we define the agentive support, in short support, of a research programme \(\mathit{ResProg}_i\) at time \(t\), i.e., \(n_i^t\), as the number of agents preferring \(\mathit{ResProg}_i\) at step \(t\). As \(n_2^t\) can be easily inferred from \(n_1^t\) (if an agent does not support one research programme, she supports the other), we will only refer to \(n_1^t\) from now on. Intuitively, the greater the support of the strongest research programme, the greater the epistemic success of the community. From our first analysis of the simulations, the most relevant factor is the difference between each research programme’s strengths. To characterize this intuition, we define the strength difference \(d \in [-1,1]\) as the difference between the strengths of the two research programmes (\(d = S_1 - S_2\) with \(S_1\) and \(S_2\) the respective strengths of \(\mathit{ResProg}_1\) and \(\mathit{ResProg}_2\)). Such a difference is positive when \(\mathit{ResProg}_1\) is stronger than or equal to \(\mathit{ResProg}_2\), and negative otherwise.
A very clear indicator of the epistemic success of a community would be if every member always preferred the strongest research programme. Yet, since our model is stochastic, an otherwise rather accurate community may sometimes end up supporting the weaker program. To have a more relaxed criterion of success, we define an epistemically successful community as a community where, on average, a majority of agents prefers the strongest program. An epistemically successful community is one where the average support for the stronger program is higher than half of the community.
We report the average support for a research programme over multiple runs with the same strength difference \(d\). We launch 10 000 simulations with the same parameters for \(\mathit{Com}\) and \(\mathit{Env}\); the strength of the research programmes is randomly generated. Then, we define \(40\) distinct values of \(d\) covering the \([-1,1]\) interval, each distant from \(0.05\), and round the strength difference of each simulation to the closest of these values: we end up with roughly \(250\) runs for each value of \(d\). For each of these runs we measure the support of each research programme at 100 steps (i.e., at \(t = 100\)), which is a reasonable convergence time, as explained in Section 5.1. Accordingly, we denote \(\overline{\mathit{Supp}}_d\) as the average support of a community \(\mathit{Com}\) at step \(100\) for a specific value of \(d\). We indicate with \(\mathit{SE}\) the standard error over the value of \(\overline{\mathit{Supp}}_d\). The standard error gives us an estimation of how \(\overline{\mathit{Supp}}_d\) could vary if we were to repeat the experiments. Notably, by averaging the value of support over 250 runs per parameter combination, we make sure the standard error is consistently low.
- \(\overline{\mathit{Supp}}_d + SE > \frac{N}{2}\), if \(d > 0\); and
- \(\overline{\mathit{Supp}}_d - SE < \frac{N}{2}\), if \(d < 0\).
We introduce intervals in order to compare the performance of different communities. Intuitively, a community \(\mathit{Com}_1\) is more epistemically successful than another community \(\mathit{Com}_2\) whenever the interval in which \(\mathit{Com}_1\) is epistemically successful is larger than the interval in which \(\mathit{Com}_2\) is so. Indeed, some communities grant a higher support to the strongest program only when the strength difference is large, while do not do so in other cases.
As a consequence, we say that a community is fully epistemically successful if for any interval \([d_1,d_2]\) and any environment obtained by the combination of values in Table 1 such community is epistemically successful.
Finally, we define the polarization ratio of a community as the ratio between the largest group of agents and the smallest group, i.e.,
| \[ \mathit{PolRat}^t = \frac{\min(n_1^t, n_2^t)}{\max(n_1^t, n_2^t)}\] | \[(5)\] |
Following Bramson et al. (2017)’s classification, this is what is called a size parity based form of polarization. The polarization ratio will help us delineate a specific bias feature in Section 5.11. For the same reasons highlighted above, we compute the average polarization ratio \(\overline{\mathit{PolRat}}\) by averaging over the values for polarization ratio at 100 steps of 250 runs per parameter combination.
Results
The main results we observe are the following.
- Non-biased communities are good at selecting the best alternative (i.e., fully epistemically successful).
- Biased communities
- are less epistemically successful than non-biased ones, but
- tend also to polarize less than non-biased ones.
- The negative impact of the bias on epistemic success can be mitigated by:
- An equal number of agents supporting each alternative in the beginning.
- A mechanism to filter out weak arguments at the community level, the "shared beliefs".
Unless specified otherwise, all the following plots and observations are made using the default values for the parameters in Table 1.
We divide the present section as follows. First, we discuss the asymptotic behaviour of our simulation, and we argue that measuring the average support at step 100 is a reasonable choice. Then, we briefly study the behaviour of a non-biased community, and we compare it with that of a biased one. Finally, we show the way shared beliefs may mitigate the negative impact of the bias.
Time convergence
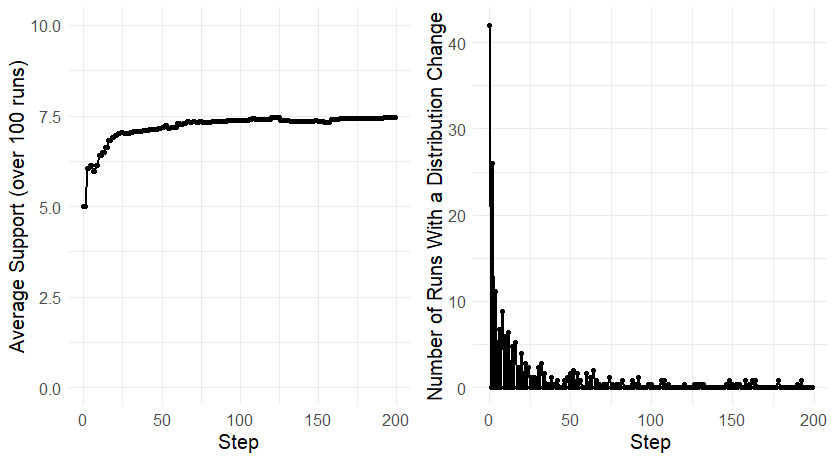
In this section, we study the asymptotic behaviour of communities. Although some communities may reach a stable situation in terms of support for each research programme, this is not the case for every parameter combination. For certain sets of parameters, no situation is stable, since there is always a non-zero probability that agents generate a set of arguments that leads one or more agents to change their preference(s).
Regardless, the number of runs in which at least one agent changes her mind at a given time-step decreases with every step (see Figure 6). And, notably, after 100 steps, almost no run undergoes any change. For this reason, we choose to evaluate the performance of a community at that time.8
In general, as time goes on, agents become less and less likely to change their minds for two reasons: first, as the agents’ views become more and more different, every agent adds to her view fewer arguments per step, as it is very likely new arguments attack arguments she is not aware of. Second, as the agents’ views become larger and larger, the addition of a new argument becomes less and less likely to change their minds.
The baseline model
We now turn to analyze the baseline model, i.e., a non-biased community with no shared beliefs (\(\mathit{bias}= 0\) and \(\mathit{shBel}= 0\)). By testing its results against our intuitions, we can ensure our modeling choices reflect our conceptual understanding of the matter. In particular, we expect such a community to be fully epistemically successful: that is, we expect most agents to prefer the stronger research programme. Similarly, we expect the average support for \(\mathit{ResProg}_1\) (that is \(\overline{\mathit{Supp}}_d\)) to increase as the difference in strength between the two research programmes (\(d = S_1 - S_2\)) increases.
Unbiased communities perform in accordance with our intuitions, as they are fully epistemically successful, and their average support for \(\mathit{ResProg}_1\) (\(\overline{\mathit{Supp}}_d\)) increases as \(d\) increases. As can be seen in Figure 7, the average support increases as the strength difference increases and is higher for \(\mathit{ResProg}_1\) when the difference is higher than zero (\(d >0\)): when \(\mathit{ResProg}_1\) is stronger, a majority of agents prefer it. In addition, when the difference in strength is large in absolute value (\(|d|>0.5\)), the community always reaches a correct consensus: baseline communities are strictly epistemically successful in the union of intervals \([-1, -0.5] \cup [0.5, 1]\). Important to note is that the value of \(S_1\) and \(S_2\) do not matter: only the difference of strength between programs determines the number of agents on each side at the end.
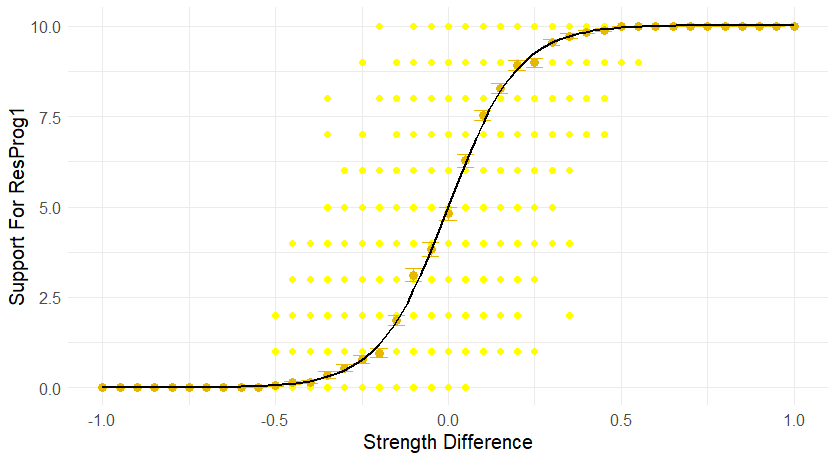
The individual data points may be found quite far away from the averaged values (Figure 7): when the absolute value of the difference is small (\(|d| < 0.5\)), \(\mathit{Supp}\) takes on many different values depending on the run. Instead, when the absolute value of the difference is large (\(|d| > 0.5\)) the support is either zero or ten, meaning the community always reaches a consensus (remember that the size of the community is ten). In fact, the greater the difference, the more the agents are pushed towards the strongest theory, up to the point in which a consensus on it is the only distribution likely to last.
The relationship between the average support (\(\overline{\mathit{Supp}}_d\)) and the strength difference (\(d\)) shown in Figure 7 can be approximated by a sigmoid model with formula:
| \[ \overline{\mathit{Supp}}_d= \frac{\alpha}{1+e^{-\beta \cdot d}}\] | \[(6)\] |
- The community is highly sensitive to any change in the strength difference when such difference is small (\(|d| < 0.25\)), that is to small changes in the strength difference correspond large changes in the average support.
- The community is less sensitive to any change in the strength difference when such difference is rather large (\(|d| > 0.5\)). The community always converges to consensus whenever the strength difference is rather large, as all agents choose the strongest theory.
The emergence of the sigmoid is robust for any parameter combination in Table 1, i.e., it is always possible to fit the sigmoid function effectively to describe the behaviour of the average support (\(\overline{\mathit{Supp}}_d\)). However, while \(\alpha\) is stable and equal to the number of agents (\(\alpha = N\)) the value for the steepness of the function (controlled by \(\beta\)) changes with respect to how the parameters change (see Appendix B).
To provide the reader with an example, we study how the steepness of the sigmoid (\(\beta\)) is influenced by the probability for agents to add an argument to their own views (\(p_{\it see}\)). As such probability decreases, the central part of the sigmoid becomes less steep. This implies that the community is less sensitive to small changes in the strength difference in such a part. Decreasing the probability of adding an argument causes the agents to be less effective in identifying the stronger theory. Indeed, the more arguments are included the more their distribution in the agents’ views is likely to reflect the strength difference between the two research programmes. If an agent only includes a part of all the produced arguments in its view, that part is more likely to be misleading.
In summary, our baseline model fits our conceptual expectations, which satisfies a basic requirement for its representational adequacy. In addition, it also features the emergence of a specific pattern, i.e., a sigmoid relationship between the average support and the strength difference, which highlights some interesting details of the performance of the community.
A biased community
Now that the behaviour of a non-biased community is clear, we proceed to answer our first research question, concerning the effect of myside bias (Section 1), by discussing the three following findings.
- The bias has a detrimental effect on communities, as biased communities are often not fully epistemically successful. In particular, biased communities tend to preserve the status quo more than unbiased communities.
- Equally distributed biased communities are fully epistemically successful, i.e., they neutralize the detrimental effect of the bias.
- Biased communities tend to be less polarized than unbiased ones.
The detrimental effect of the bias
Biased communities are usually less epistemically successful than non-biased ones. A biased community mainly differs from a non-biased one because the initial support for the research programmes, i.e., how the agents are divided initially in terms of preferences, influences the evolution of agents’ preferences. In a non-biased community the initial support does not matter. In a biased community, if a majority of agents support \(\mathit{ResProg}_1\) initially (\(n_1^0 > \frac{N}{2}\)) the average support for \(\mathit{ResProg}_1\) will be higher than if the community was not biased, while if the initial support for \(\mathit{ResProg}_1\) is a minority (\(n_1^0 < \frac{N}{2}\)), the final average support for \(\mathit{ResProg}_1\) will be lower (see Figure 8). Therefore, if there is a clear majority preferring one side at the beginning of the debate (\(n_1^0 \neq \frac{N}{2}\)), a biased community is not fully epistemically successful: the average support will be higher for the weaker research programme for a certain interval of values of the strength difference.10 For example, if nine out of ten agents start our preferring \(\mathit{ResProg}_1\) (as in the green line in Figure 8) the average support is higher for \(\mathit{ResProg}_1\) even if \(\mathit{ResProg}_2\) is stronger than \(\mathit{ResProg}_1\) of a value \(0.2\) (that is when \(d = \mathit{ResProg}_1 - \mathit{ResProg}_2 = - 0.2\)).
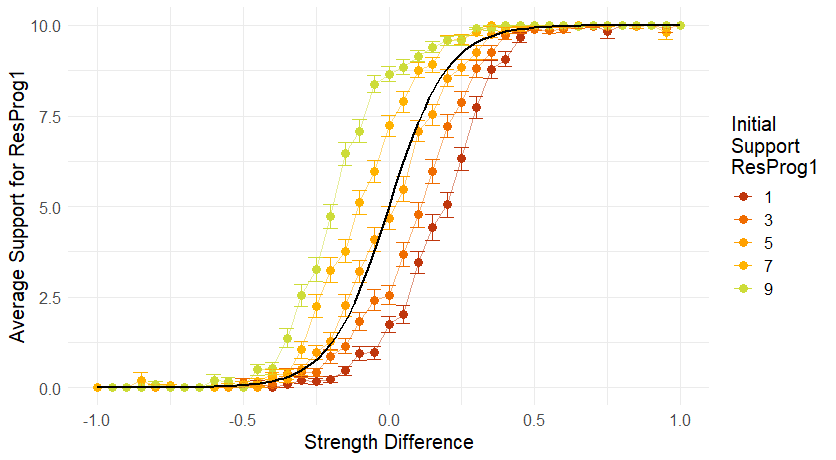
In particular, given a certain value for the bias, the further away is the initial support for \(\mathit{ResProg}_1\) from half the size of the community, the smaller the interval in which a community is epistemically successful, as shown in Figure 8. In this sense, we say that biased communities tend to preserve the status quo, as they tend to provide more support for the program that was preferred in the beginning. A similar mechanism is observed for the value of the bias: the greater the bias, the smaller the epistemically successful interval, as the more the average values depart from the baseline results (see the comparison with \(\mathit{shBel}= 0\) between \(\mathit{bias}= 0.3\) and \(\mathit{bias}= 0.5\) in Figure 10).11
The results of a biased community can also be approximated by Equation 6. To do so, we introduce a generalized notion of strength difference, which allows us to use Equation 6 to fit the results of biased and unbiased communities. We call this refined notion of strength difference biased strength difference.
The biased strength difference is derived from the initial distribution of agents, their bias and the strength of the two research programmes. It can be understood as a weighted average of both groups’ probabilities of generating attacks against each research programme at the beginning of the debate. The biased strength difference generalizes the strength difference since, in case \(\mathit{bias}= 0\), we have \(d_{\mathit{bias}} = d\).
Observation 1. Using the biased strength difference (\(d_{\mathit{bias}}\)), we can describe all the results obtained so far (that is, those in Figure 8 and Figure 7) as follows:
| \[ \overline{\mathit{Supp}}_{d_{\mathit{bias}}}= \frac{\alpha}{1+e^{-\beta \cdot d_{\mathit{bias}}}},\] | \[(7)\] |
This is remarkable for two reasons. On the one hand, it is interesting that despite the combinatorial complexity of the protocol, we can derive the average support using a simple formula, which only depends on the initial conditions. On the other hand, it allows us to understand the behaviour of a biased community with the same mechanism as an unbiased one. A biased community dealing with two research programmes with strength \(S_1\), \(S_2\) and with a certain biased strength difference (\(d_{\mathit{bias}}\)) produces the same average support as a non-biased community in the same environment dealing with two research programmes with strengths \(S_1'\) and \(S_2'\) such that its correspondent strength difference is the same of the biased strength difference (\(d' = d_{\mathit{bias}}\)). It is as if a biased community perceives the two research programmes as having different strengths, which are influenced not only by the bias but also by the number of people supporting each theory initially.
Equally distributed biased communities
Our results show that the community \(\mathit{Com}\) is fully epistemically successful when there is an equal number of agents preferring each research programme at the beginning (\(n_1^{0} = \frac{n}{2}\)). We call these communities "equally distributed", referring to their initial distribution of support. Consider again Figure 8: when the initial support for \(\mathit{ResProg}_1\) is five (\(n_1^{0} = 5\)), the final average support is the same as when the community is not biased.13 This suggests that an equal initial distribution of agents cancels out the impact of the bias.
These results align with the conjecture by Mercier & Heintz (2014) that collective reasoning is less affected by the detrimental impact of myside bias than the individual one. In our model, if a community is composed only of one individual, it would never be epistemically successful (as there is no way to distribute equally only one agent); on the other hand, a biased community of more than one scientist may be equally distributed and thus, epistemically successful. Such an observation further validates our simulation.
In summary, biased communities are not epistemically successful, as the bias makes communities more inclined to produce a higher average support for the research programme that was more supported initially, even if it is not the objectively stronger one. Such an effect is positively correlated with the intensity of the bias; yet, quite surprisingly, it does not come into play if the community is initially equally distributed.14
More bias, less polarization
Finally, we also discuss the effect of bias on the polarization of a community. As can be noted from Figure 9 more biased communities tend to polarize less, that is to exhibit a lower average polarization ratio.
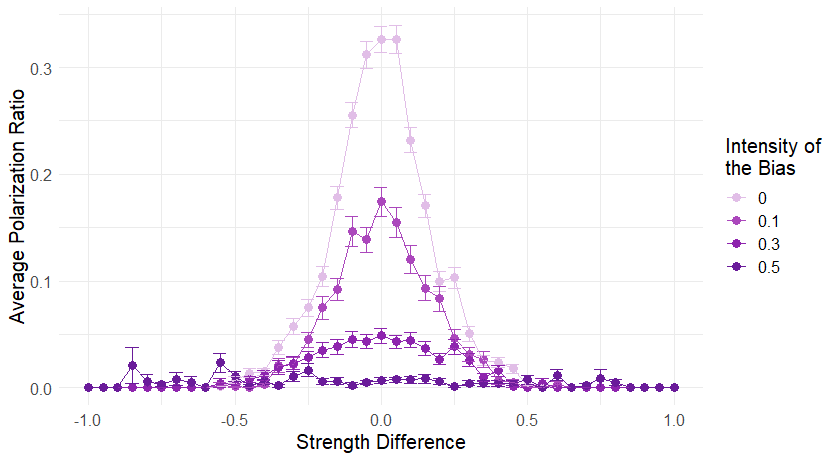
Although this result may perhaps seem surprising, it is easily explained. Biased communities are not more likely than non biased ones to form a consensus. Yet, when the agents of a biased community end up preferring all the same program they are very likely to not change their preferences ever again. Indeed, in such a situation agents are highly unlikely to produce enough arguments against the community current preferred research programme to change someone’s mind. As a consequence, even if non-biased communities are equally likely to form consensus as biased ones, consensus is way more stable in the latter. This explains why biased communities exhibit a lower average polarization ratio.
Results with shared beliefs
To check the effectiveness of the shared beliefs filter, we study how a biased community with a certain degree of shared beliefs compares to a baseline community: the closer the behaviour of the biased community to that of the baseline community, the more the shared belief filter has a mitigating effect.
We find that shared beliefs do reduce the detrimental impact of the bias, but this effect is quite limited. To see this consider the lower line of plots of Figure 10, where we represent the average support of different rather biased communities (\(\mathit{bias}= 0.5\)) with respect to the average support of a similar non-biased community. The red points describe the average support of a biased community with an initial support of one (\(n^0_1 = 1\)), the green ones the average support of a biased community with initial support of nine (\(n^0_1 = 9\)), and finally the black line represents the sigmoid approximation of the average support in a similar non-biased community. As the shared beliefs parameter \(\mathit{shBel}\) increases, the average supports of the biased communities get closer to this baseline approximation: a rather biased community (\(\mathit{bias}= 0.5\)) is epistemically successful in a greater interval for \(d\) when \(\mathit{shBel}\) increases. Yet, even when the degree of shared beliefs is at its maximum, the initial support of \(\mathit{ResProg}_1\) still influences the final average support (\(\overline{\mathit{Supp}}\)) as the community is not yet completely epistemically successful (which can be seen by the fact that the green and red points do not follow the black sigmoid).
In addition, when the bias is quite low, the effect of the shared beliefs is almost invisible: consider the first line of Figure 10, where there is none to little difference between the three plots. Since the shared beliefs lead to a suppression of weak arguments, their mitigating effect on the bias works best when the bias allows agents to produce a lot of weak arguments. This is not the case when the bias is small.
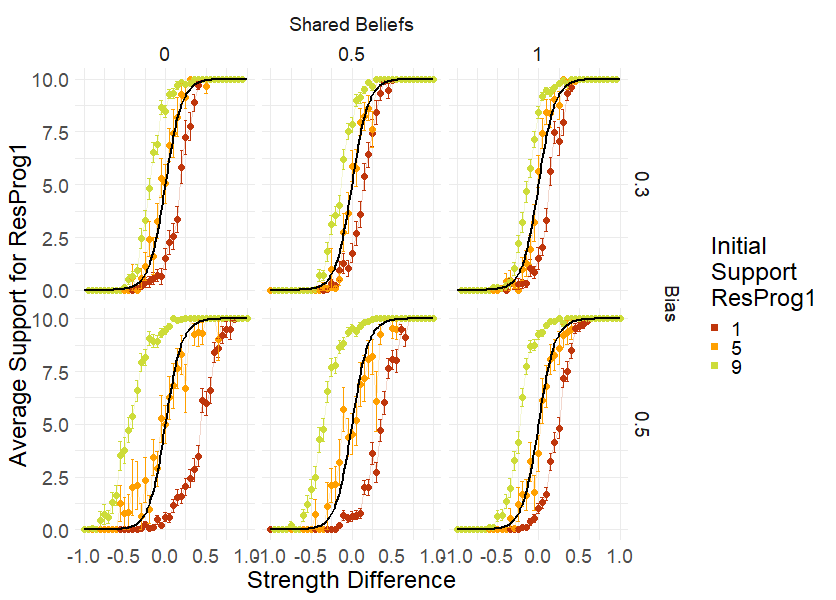
Similarly, shared beliefs are ineffective in mitigating the bias’s impact when the difference between the strength of the two research programmes is very small (\(d\) close to \(0\)). This can be seen in Figure 10, as the distance between the average support for the biased community and the sigmoid approximation does not diminish much in the central area of each plot, that is when the difference is the smallest. Shared beliefs help agents to discriminate between good and bad arguments, but in such area all arguments have more or less the same strength. Consequently, in those situations, shared beliefs are not very effective.
Related Works
We now provide a brief comparison of our approach and extant studies while underlining the novelty of our model. Although no previous ABM has studied myside bias as a production bias in the context of argumentation, many ABMs have been proposed to either study cognitive biases in the context of scientific inquiry or opinion dynamics in argumentative contexts. We compare our work to both these two streams of literature.
Previous ABMs based on abstract argumentation have been used to study opinion dynamics and polarization effects in argumentative settings (Banisch & Olbrich 2021; Butler et al. 2019; Gabbriellini & Torroni 2014; Mäs & Flache 2013; Proietti & Chiarella 2023; Singer et al. 2018; Taillandier et al. 2021), gradual learning in debates (Dupuis de Tarlé et al. 2022), network effects in the context of scientific inquiry (Borget al. 2017b; Borg et al. 2018), or argumentation-based procedures for how to choose among scientific theories (Borg et al. 2019). In terms of modeling framework, the main differences between our model and this stream of literature are mainly two.
First, our model allows for a more natural process of argument generation: any agent can investigate any argument, and possibly attack it. Attacks may be weak or strong depending on where they are directed to. This represents the features of a deliberative process, in which the discussants can create arguments that may not always be convincingly strong, and also allows us to include myside bias as a production bias easily. This is not the case for either of the past models, in which either the arguments are a finite set and can be learnt just by meeting someone who already possesses them (Banisch & Olbrich 2021; Dupuis de Tarlé et al. 2022; Mäs & Flache 2013; Proietti & Chiarella 2023; Singer et al. 2018; Taillandier et al. 2021), or the arguments are a finite number and can only be discovered as pieces of evidence by scientists who look into the right place (Borg et al. 2019, 2018).
Second, our model introduces a new mechanism to evaluate the epistemic outcome of the discussion. This is, again, a novel feature that more traditional models do not usually have, as they are not concerned with the epistemic impact of a mechanism but rather with the dynamics it generates.
Although no model allows for the representation of myside bias as a production bias, computational models have been used to capture the effects of cognitive biases intended as evaluation biases. Liu et al. (2015), Fu & Zhang (2016), Banisch & Shamon (2023), Proietti & Chiarella (2023), Dupuis de Tarlé et al. (2022) all model biased agents as agents who are more likely to ignore arguments against their present position than arguments in favour of it. Such agents exhibit an evaluation bias, insofar as they fail to evaluate arguments impartially. In addition, Gabriel & O’Connor (2024), Baccini & Hartmann (2022), Baccini et al. (2023) model evaluative biases in a Bayesian framework. They consider the exchange of arguments as an exchange of evidence, and understand biased agents as agents who discount evidence against their own current position. Finally, in Proietti & Chiarella (2023) and Singer et al. (2018) biased agents tend to forget arguments opposed to their present views sooner than the other ones.
Most of these models find that biased communities polarize more often or that polarization is usually expected to last longer. In contrast to them, our results suggest that if myside bias is understood only as a production bias, i.e., a tendency to produce arguments only in favour of one’s view, biased communities are less likely to be found in a polarized state. This suggests that polarization is affected in different ways by various forms of myside bias. However, a more thorough comparison of the results of these two types of myside bias is needed before drawing any conclusion, as our results only take into account one of the possible measures of polarization (Bramson et al. 2017), and a specific setting in which the bias can emerge.
Among the many articles that study the effect of biases in deliberative settings, Gabriel & O’Connor (2024), Baccini et al. (2023) are the only ones who look at the epistemic performance of a community. Baccini et al. (2023) provide a bayesian interpretation of myside bias as an evaluation bias, based on their previous work (Baccini & Hartmann 2022), and explore under which conditions biased agents outperform non-biased ones. They find that this is the case mostly when the size of the deliberating community is small and agents start the discussion with already a favourable prior belief in the correct hypothesis. Gabriel and O’Connor (2024) investigate the effect of bias for scientific inquiry whenever scientists need to choose which theory to use among two. They show that moderate levels of confirmation bias, as a skewed evidence evaluation, can help scientists to reach an accurate consensus more often.
Conclusion and Outlook
We used multi-agent modeling and abstract argumentation to represent a community of scientists debating two distinct research programmes. We tested our model against general conceptual expectations and registered the emergence of a specific relationship between the average support for a research programme and the strengths of the two research programmes. Namely, the greater the difference of strength between the two research programmes, the more agents will successfully prefer the stronger one.
Following Mercier & Heintz (2014) and Mercier (2017), we introduced the possibility for agents to be biased when producing new arguments. We measured the detrimental effect of myside bias by showing that biased communities are usually not fully epistemically successful, as they may produce higher average support for a weaker research programme if such a research programme had more initial support. We discovered that this harmful effect of the bias is not present in communities that are equally distributed, that is when a similar number of agents supports each research programme at the beginning. In addition, we also showed that biased communities tend to polarize less than non-biased ones. This result stands in sharp contrast with results concerning more classical types of ‘evaluation biases’, such as those obtained by Mäs & Flache (2013), Proietti & Chiarella (2023), Singer et al. (2018) who find that biased communities polarize more.
Finally, we have demonstrated that communities with more shared beliefs for the evaluation of arguments can mitigate the detrimental effect of the bias. However, the beneficial effect of shared beliefs cannot completely cancel the impact of bias, and becomes rather negligible when the two research programmes have a similar strength. In this way we confirmed and qualified a conjecture by Mercier & Heintz (2014).
In light of these results, our contribution is twofold. On the one hand, we have provided a simulation-based test for previously proposed hypotheses, such as those by Mercier & Heintz (2014). On the other hand, we have made a first step in offering a more systematic understanding of the impact of myside bias on the collective performance of scientists.
Our findings hinge on a number of assumptions. First, we assume the objective strength of the research programmes to not be visible to the agents, but to only influence the process of argument generation. Accordingly, we measure the performance of a scientific community based on its ability to identify the strongest between two scientific programs. We assume the two scientific programs to have the same number of central arguments: each program has a specific strength and this strength is assigned to each of its central arguments. Agents aim at eliciting which program is the strongest by looking for counter-arguments to central arguments, or by attempting to defend them. This idealized picture of scientific debate allows us to focus on the effect of myside bias, and bracket many of the complex details of scientific inquiry. However, future work may be directed at relaxing these assumptions and study the robustness of our results with a more nuanced representation of science. For example, a research programme with a significantly higher number of central arguments than the other may make the task of scientists easier – and, consequently, mitigate the detrimental effect of the bias.
We also represent scientists as impartial in evaluation arguments and high performing agents. They remember every argument they learn, and, they always support the most promising and solid theory, regardless of whether they are biased or not. This assumption captures Mercier and Sperber’s account of myside bias, which they take to not affect argument evaluation: agents are always willing to change their minds when presented with enough arguments (Mercier & Sperber 2017). If agents were more steadfast in their preferences, the bias may cause a more polarized situation, and the initial distribution of agents may have an even stronger impact.
Although our model aims at representing scientific debates, it can be easily applied to any debate in which these assumptions are reasonable. Consider, for example, a committee of urban planners discussing two possible ways of building a stadium. Under the assumption that there is an objectively superior option, e.g., because it would make spectators safe, or would make the energetic system more efficient, one could model the discussion leading to their decision in our framework.
Our study opens ample space for future work. While we have shown that equally distributed groups may be able to cancel the detrimental effect of the bias, new questions arise. On the one hand, which incentive structures can help communities obtain such a division of labor? On the other hand, are there other mechanisms that lower the detrimental effect of myside bias? Mercier & Heintz (2014) propose a high degree of interactivity of scientific communication to overcome fragmentation of argumentative exchanges (p. 521). A possible approach is to link this feature with the work on adversarial collaboration by Clark & Tetlock (2021).
Another open question concerns the effectiveness of shared standards of argument evaluation in our model, which are helpful only if one research programme is clearly stronger than the other. This raises the question: can shared standards also help communities if the rival research programmes are similar in strength, and if so, how? Are there some additional mechanisms that support the mitigating role of shared standards?
As noted by Mercier & Heintz (2014), Dutilh Novaes (2018), when a myside biased agent fails to predict potential defeaters to one of her produced arguments, she risks not being able to reply to criticism. This in turn may negatively affect her reputation. Reputation management and decision making under uncertainty are thus important features to consider in future iterations of our model.
Notes
- The term myside bias was coined in an unpublished manuscript by Perkins from 1986, eventually published in Perkins (2019).↩︎
- A description of the model following the ODD protocol and the source code can be found on the CoMSES database: https://www.comses.net/codebase-release/49d2dbe8-7f8e-43f2-a27f-87afdac7f5f7/↩︎
- It is worth noticing that the other semantics defined in Dung (1995) coincide with the grounded semantics in the AFs underlying our ABM, which are trees by construction (see Section 3.1).↩︎
- Although central arguments do not attack each other, they can be incompatible (Šešelja & Straßer 2013), insofar as they reach opposite conclusions. Because agents only support one research programme at a time, they never end up supporting incompatible arguments.↩︎
- Note that the strength of each research programme is not accessible to the agents and thus does not directly impact their preferences. However, it affects agents’ preferences indirectly via the influence it has on the process of argument generation.↩︎
- Agents produce arguments simultaneously. To keep things simple and focused on the effects of myside bias, we avoid modeling priming effects.↩︎
- For instance, the variability of the quality of grant proposals (as judged by the reviewers) submitted to the Austrian Science Fund (between 1999 and 2009) is twice as high in the social sciences than in the natural sciences (Mutz et al. 2012). Similarly, the reviewers’ ratings (in terms of their inter-rater reliability) vary considerably more in the former when compared to the latter field.↩︎
- We checked that this is the case in communities as large as 100 agents, and did not find any effect of the size of the population on the results.↩︎
- For the default values, \(\beta = 9.3\) and the residual standard error is 0.1045 on 39 degrees of freedom, i.e., 39 different values for \(d\): \(0, 0.05, 0.1, 0.15, ...1\).↩︎
- We observed this behaviour for a bias as lower as \(0.05\). When the bias gets lower than that value, it is hard to distinguish whether or not there is any statistical difference between a situation with \(\mathit{bias}= 0\).↩︎
- Although this behaviour can be observed through the whole parameter space, i.e., for any possible parameter combination studied (see Table 1), it is worth highlighting the slightly different behaviour of what we call Limit cases. As the probability of attacking a research programme cannot exceed 1, sometimes the bias may provide a ‘bonus’, that is smaller than its numerical value. Consequently, it may be the case that one research programme is more ‘helped’ by the bias than the other. Although such detail does not have a major impact, the results change slightly when the bias is strong. In particular, it can be the case that when \(n_1^0 = 5\), the average values do not precisely follow the baseline model. For example, assume \(d = 0.25\) and \(\mathit{bias}= 0.4\); if \(S_1 = 0.8\) and \(S_2 = 0.55\), the average support for \(\mathit{ResProg}_1\) is lower than if \(S_1 = 0.6\) and \(S_2 = 0.35\). ↩︎
- Again, for the default values, \(\beta = 9.3\) and the residual standard error is 0.76 on 39 degrees of freedom, i.e., 39 different values for \(d_{\mathit{bias}}: 0, 0.05, 0.1, 0.15, ...1\).↩︎
- This is the case under the assumption that we do not incur in ‘limit cases’ - see Endnote 11.↩︎
- Appendix C analytically investigates the behaviour of a community of two agents. This may help understanding what makes equally distributed biased communities behave exactly like non-biased ones.↩︎
Appendix A: Algorithm for Computing the Acceptable Arguments
This algorithm for generating the grounded labelling starts by selecting all arguments that are not attacked, and then iteratively: any argument that is attacked by an argument that has just been selected in the extension is considered unacceptable, and then we add to the extension the arguments all of whose attackers are unnacceptable.
In our setting, the arguments which are not attacked are the leafs of each argumentation tree.
Appendix B: Additional Results
Table 2 register how different parameters of \(\mathit{DebSet}\) affect the coefficient \(b\) of the function
| \[ \overline{\mathit{Supp}}= \frac{\alpha}{1+e^{- \beta \cdot d}}.\] | \[(8)\] |
As mentioned in the main article, the if \(\beta\) increases, the steepness of the curve also increases, which makes the community more sensitive to changes in the area around \(d = 0\) and less sensitive to changes in most distant areas.
| Parameter | Impact on \(\beta\) |
|---|---|
| \(p_{\it see}\) | \(\beta\) increases. |
| \(N_{CA}\) | \(\beta\) increases. |
| \(\mathit{StDev}\) | \(\beta\) decreases. |
Appendix C: Analytical Analysis of Equally Distributed Communities
To substantiate the (quite surprising) computational finding that biased equally distributed communities are fully epistemically successful, we provide an analytical result about such communities. To do so, we restrict our analysis to a simple case, where we show that our computational results are corroborated. Indeed, as the number of steps increases, the number of possible states of the model grows rapidly, which renders a mathematical analysis very challenging.
We compare two communities, a biased and a non biased one. Each community is composed of two agents, where one agent prefers \(ResProg_1\) and the other prefers \(ResProg_2\). Crucially, we find that after one round of simulation the expected number of agents supporting \(ResProg_1\) in a case in which agents are biased is the same as in a case in which agents are not biased. Formally, this amounts to the following.
Observation 2. Let \(Com = \langle N, n_1^0, p_{\mathit{see}}, bias \rangle\) and \(Com' = \langle N, n_1^0, p_{\mathit{see}}, bias' \rangle\) be two communities with \(N = 2, p_{\mathit{see}} = 1, n_1^0 = 1\), \(bias = 0\) and \(bias' >0\). For any environment \(Env, S_1, S_2\) such that \(S_1, S_2 \in \: ]bias', 1- bias'[0 < S_1 - c, 0 < S_2 - c, S_1 + c < 1\) and \(S_2 + c < 1\) and \(N_{CA} = 1\), the expected value of the support \(n_1^t\) at time \(t = 1\) (with possible outcomes \(\{0,1,2\}\)) is the same for \(Com\) and \(Com'\).
If confronted with the same environment \(Env\), two equally distributed communities of two agents have the same expected value of support \(n_1^t\) at time \(t =1\) even if one community is biased and the other is not.
Proof. First we shall specify more formally the notion of expected value. Given a debate setting \(DebSet\) with \(|N| = 2\), it is possible to define an event space \(\omega_n = \{ 0, 1, 2\}\) which contains every possible outcome for the variable \(n_1^1\). In addition, based on how each action of the agents is defined in the protocol, it is possible to assign to each of these events a probability \(P: \omega_n \mapsto [0,1]\). Consequently, when talking about expected value \(\mathbb{E}\) for \(n_1^1\), we consider it to be the following: \(\mathbb{E}(n_1^1) = P(n_1^1 = 2) \cdot 2 + P(n_1^1 = 1) \cdot 1\). Notably, the probability \(P(n_1^1 = i)\) can be computed by computing the probability of even more elementary events, e.g. the event that one of the two agents decides to attack one argument. We consider an environment where \(N_{CA} = 1, StDev = 0.2\) and two communities \(Com\) and \(Com'\) where \(N = N', n_1^0 = n_1^{0'}\), \(p_{\mathit{see}}\) = \(p'_{\mathit{see}} = 1\) and \(0 = bias < bias'\).
By definition, \(\mathbb{E}(n_1^1) = P(n_1^1 = 2) \cdot 2 + P(n_1^1 = 1) \cdot 1\), and, similarly, for \(\mathbb{E}(n_1^{1'})\). We shall denote with \(A\) the agent who starts with a preference for \(ResProg_1\) and \(B\) the one who starts preferring \(ResProg_2\). We denote with \(C_1\) and \(C_2\) the central arguments of \(ResProg_1\) and \(ResProg_2\) respectively. During the first step of the debate, each agent can either attack \(C_1'\), attack \(C_2'\) or produce no attack. We define the event \(Att(C_i) = k'\) as the event in which after the first step, the number of attacks against \(C_i\) is \(k\).
For an agent to change her mind, the score of the other \(ResProg\) must be strictly superior to the score of her currently preferred \(ResProg\). Because we consider \(p_{\it see} = 1\) and thus the agents are aware of all the attacks which are produced, we have the following inequalities:
- \(P(n_1^1 = 2) = P((Att(C_2) = 2 \cap Att(C_1)) = 0) \cup (P(Att(C_2) = 1 \cap Att(C_1) = 0))\)
- \(P(n_1^1 = 1) = (P(Att(C_2) = 0 \cap Att(C_1) = 0)) \cup (P(Att(C_2) = 1 \cap Att(C_1) = 1))\)
The same holds for when we talk about a biased community. To show when we are considering a biased community, we use the notation \(P_{bias}\), e.g. \(P_{bias}(Att(C_2) = 2 \cap Att(C_1) = 0))\) refers to the probability of obtaining to attacks against \(C_1\) and none against \(C_1\) with a biased community.
We proceed as follows.
- We prove, extensively, that \(P(Att(C_2) = 1, Att(C_1) = 0) = P_{bias}(Att(C_2) = 1, Att(C_1) = 0)\), i.e., that both the biased community and the unbiased one have the same probability of producing an argument against \(C_2\).
- Thus, we mention, briefly that following the same steps as above the following can be proven:
- that \(P(Att(C_2) = 0, Att(C_1) = 0) = P_{bias}(Att(C_2') = 0, Att(C_1') = 0)\),
- \(P(Att(C_2) = 2, Att(C_1) = 0) = P_{bias}(Att(C_2) = 2, Att(C_1) = 0) + \frac{bias^2}{4}\), and that
- \(P(Att(C_2) = 1, Att(C_1) = 1) = P_{bias}(Att(C_2) = 1, Att(C_1) = 1) - \frac{bias^2}{2}\).
- Finally, we combine every statement together and we prove the initial observation.
Through the first point, we hope to give the reader a feeling of how all the other computations should be done, and we then leave them out in the second point.
Claim 1. We shall prove that \(P(Att(C_2) = 1, Att(C_1) = 0) = P_{bias}(Att(C_2) = 1, Att(C_1) = 0)\). In short, the probability of the first step ending with one attack on \(C_1\) and none on \(C_2\) is the same for both biased agents and unbiased ones.
Figure 11 presents a schematic view of the probability tree associated with this problem. We use the following names of events.
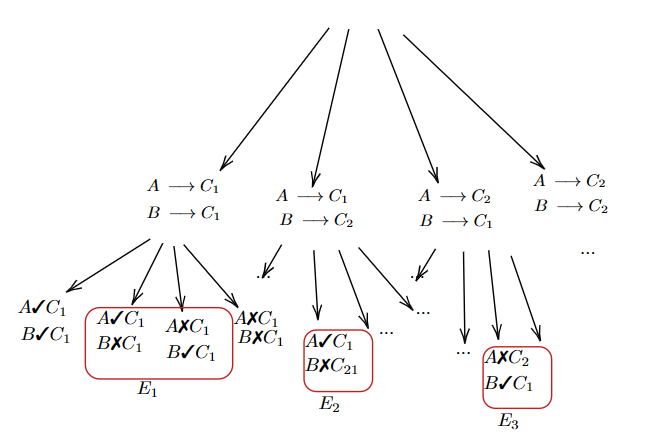
- \(A\) (resp. \(B\)) \(\longrightarrow C_i\): Agent \(A\) (resp. \(B\)) is investigating argument \(C_i\).
- \(A\) (resp. \(B\)) ✔ \(C_i\): Agent \(A\) (resp. \(B\)) has produced an attack against \(C_i\).
- \(A\) (resp. \(B\)) ✗ \(C_i\): Agent \(A\) (resp. \(B\)) has failed to produce an attack against \(C_i\).
We shall start with the case for community \(Com\), where \(bias = 0\). First, we notice that the event \(E = Att(C_1) = 1 \cap Att(C_2) = 0\) is the union of three events circled in red in Figure 11.
\(E = E_1 \cup E_2 \cup E_3\) with:- \(E_1 = (A \longrightarrow C_1 \cap B \longrightarrow C_1) \cap [ (A\) ✔ \(C_1 \cap B\) ✗ \(C_1) \cup (A\) ✗ \(C_1 \cap B\)✔ \(C_1) ]\)
- \(E_2 = (A \longrightarrow C_1 \cap B \longrightarrow C_2) \cap (A\) ✔ \(C_1 \cap B\) ✗ \(C_2) ]\)
- \(E_3 = (A \longrightarrow C_2 \cap B \longrightarrow C_1) \cap (A\) ✗ \(C_2 \cap B\)✔ \(C_1) ]\)
\(E_1\) corresponds to the case where both agents investigate \(C_1\) but only one of them produces an attack, while \(E_2\) and \(E_3\) are the cases where each agent targets a different argument and only the attack against \(C_1\) succeeds.
Now, let's express the probabilities of \(E_1\), \(E_2\) and \(E_3\) with and without bias.
First, each event of the form \(A \longrightarrow C_i \cap B \longrightarrow C_j\) has a probability of \(\frac{1}{4}\). Now, if there is no bias, each agent has the same probability of attacking an argument \(C_i\):
- \(i \in {1,2}, P(A ✔ C_i) = P(B ✔ C_i) = 1 - S_i\),
- \(i \in {1,2}, P(A ✗ C_i) = P(B ✗ C_i) = S_i\).
| \[P(E_1) = \frac{1}{4}[2S_1(1-S_1).\] |
| \[(P(E_3) = P(E_2) = \frac{1}{4}(1-S_1)S_2.\] |
| \[ P(E) = \frac{1}{2}(1-S_1)(S_1 + S_2).\] |
Consider \(Com'\) with \(bias > 0\). The event \(E\) behaves exactly in the same way and it can also be considered as the union of \(E_1, E_2\) and \(E_3\). In this case, the probabilities of attacking either argument varies for each agent based on her preference: \(A\) is more likely to attack \(C_2\) and less likely to attack \(C_1\), and vice versa.
- \(P_{bias}(A ✔ C_1) = 1 - S_1 - bias\)
- \(P_{bias}(A ✔ C_2) = 1 - S_2 + bias\)
- \(P_{bias}(A ✗C_1) = S_1 + bias\)
- \(P_{bias}(A ✗ C_2) = S_2 - bias\)
- \(P_{bias}(B ✔ C_1) = 1 - S_1 + bias\)
- \(P_{bias}(B ✔ C_2) = 1 - S_2 - bias\)
- \(P_{bias}(B ✗ C_1) = S_1 - bias\)
- \(P_{bias}(B ✗C_2) = S_2 + bias\)
| \[P_{bias}(E_1) = \frac{1}{4}[(1-S_1 -bias)(S_1-bias) + (1-S_1-bias)(S_1+bias)] = \frac{1}{2}(S_1 - S_1^2 + bias^2),\] |
| \[P_{bias}(E_2) = \frac{1}{4}(1-S_1 -bias)(S_2-b),\] |
| \[P_{bias}(E_3) = \frac{1}{4}(S_2 - bias)(1-S_1 + bias).\] |
By developing and adding each term we obtain
| \[P_{bias}(E) = \frac{1}{4}(2S_1 - 2S_{1^2} + 2b^2 + S_2 + b - S_1 S_{2S1}b - S_2b - b^2 + S_2 - S_1S_2 + S_2b - b + bS_1 - b^2),\] |
which simplifies to:
| \[P_{bias}(E) = \frac{1}{2}(S_1 + S_2 - S_1 - S_2 -S_1S_2) = \frac{1}{2}(1-S_1)(S_1 + S_2).\] |
Notably, \(P(E) = P_{bias}(E)\).
Claim 2. Following the same mechanism as before it is possible to show that:
- that \(P(Att(C_2) = 0, Att(C_1) = 0) = P_{bias}(Att(C_2) = 0, Att(C_1) = 0)\),
- \(P(Att(C_2) = 2, Att(C_1) = 0) = P_{bias}(Att(C_2) = 2, Att(C_1) = 0) + \frac{bias^2}{4}\), and that
- \(P(Att(C_2) = 1, Att(C_1) = 1) = P_{bias}(Att(C_2) = 1, Att(C_1) = 1) - \frac{bias^2}{2}\).
Claim 3. Consequently,
| \[\mathbb{E}(n_1^1) = 1 \cdot P(Att(C_2) = 0, Att(C_1) = 0) + 1 \cdot P(Att(C_2) = 1, Att(C_1) = 1) +\\ + 2 \cdot P(Att(C_2) = 1, Att(C_1) = 0) + 2 \cdot P(Att(C_2) = 2, Att(C_1) = 0), \] |
| \[ \mathbb{E}(n_1^{1'}) = 1 \cdot P_{bias}(Att(C_2) = 0, Att(C_1) = 0) + 1 \cdot P_{bias}(Att(C_2) = 1, Att(C_1) = 1) +\] |
| \[+ 2 \cdot P_{bias}(Att(C_2) = 1, Att(C_1) = 0) + 2 \cdot P_{bias}(Att(C_2) = 2, Att(C_1) = 0) =\] |
| \[= 1 \cdot P(Att(C_2) = 0, Att(C_1) = 0) + 1 \cdot (P(Att(C_2) = 1, Att(C_1) = 1) + \frac{bias^2}{2}) +\] |
| \[+ 2 \cdot P(Att(C_2) = 1, Att(C_1) = 0) + 2 \cdot (P(Att(C_2) = 2, Att(C_1) = 0) - \frac{bias^2}{4}) = \] |
| \[1 \cdot P(Att(C_2) = 0, Att(C_1) = 0) + 1 \cdot P(Att(C_2) = 1, Att(C_1) = 1) + \] |
| \[+2 \cdot P(Att(C_2) = 1, Att(C_1) = 0) + 2 \cdot P(Att(C_2) = 2, Att(C_1) = 0)\] |
Thus, \(\mathbb{E}(n_1^1) = \mathbb{E}(n_1^{1'})\), i.e., the expected value for the average support is the same for a biased and a non biased community.
The bias does not induce changes in the agents' expected final distribution. It boils down to showing that although the probabilities of finding attacks are distributed differently, the biases compensate each other and the expected value for \(n_1^1\) is indeed the same in both cases. Thus, we have an indication as to what happens in larger equally distributed communities, that is that when two groups of equal size are biased they cancel any advantage the bias might otherwise grant to one side of the debate.
References
BACCINI, E., Christoff, Z., Hartmann, S., & Verbrugge, R. (2023). The wisdom of the small crowd: Myside bias and group discussion. Journal of Artificial Societies and Social Simulation, 26(4), 7. [doi:10.18564/jasss.5184]
BACCINI, E., & Hartmann, S. (2022). The myside bias in argument evaluation: A Bayesian model. Proceedings of the Annual Meeting of the Cognitive Science Society.
BANISCH, S., & Olbrich, E. (2021). An argument communication model of polarization and ideological alignment. Journal of Artificial Societies and Social Simulation, 24(1). [doi:10.18564/jasss.4434]
BANISCH, S., & Shamon, H. (2023). Biased processing and opinion polarization: Experimental refinement of argument communication theory in the context of the energy debate. Sociological Methods & Research, 2023. [doi:10.1177/00491241231186658]
BARON, J. (1995). Myside bias in thinking about abortion. Thinking & Reasoning, 1(3), 221–235. [doi:10.1080/13546789508256909]
BORG, A., Frey, D., Šešelja, D., & Straßer, C. (2017a). An argumentative agent-based model of scientific inquiry. In S. Benferhat, K. Tabia, & M. Ali (Eds.), Advances in Artificial Intelligence: From Theory to Practice (pp. 507–510). Cham: Springer International Publishing. [doi:10.1007/978-3-319-60042-0_56]
BORG, A., Frey, D., Šešelja, D., & Straßer, C. (2017b). Examining network effects in an argumentative agent-based model of scientific inquiry. In A. Baltag, J. Seligman, & T. Yamada (Eds.), Logic, Rationality, and Interaction (pp. 391–406). Berlin Heidelberg: Springer. [doi:10.1007/978-3-662-55665-8_27]
BORG, A., Frey, D., Šešelja, D., & Straßer, C. (2019). Theory-choice, transient diversity and the efficiency of scientific inquiry. European Journal for Philosophy of Science, 9(2), 1–25. [doi:10.1007/s13194-019-0249-5]
BORG, A. M., Frey, D., Šešelja, D., & Straßer, C. (2018). Epistemic effects of scientific interaction: Approaching the question with an argumentative agent-based model. Historical Social Research, 43(1), 285–309. [doi:10.1007/978-3-662-55665-8_27]
BRAMSON, A., Grim, P., Singer, D. J., Berger, W. J., Sack, G., Fisher, S., Flocken, C., & Holman, B. (2017). Understanding polarization: Meanings, measures, and model evaluation. Philosophy of Science, 84(1), 115–159. [doi:10.1086/688938]
BROCK, W. A., & Durlauf, S. N. (1999). A formal model of theory choice in science. Economic Theory, 14, 113–130. [doi:10.1007/s001990050284]
BUTLER, G., Pigozzi, G., & Rouchier, J. (2019). An opinion diffusion model with deliberation. 20th International Workshop on Multi-Agent-Based Simulation (MABS 2019). [doi:10.1007/978-3-030-60843-9_7]
CLARK, C., & Tetlock, P. (2021). Adversarial collaboration: The next science reform. In C. L. Frisby, R. E. Redding, W. T. O’Donohue, & S. O. Lilienfeld (Eds.), Ideological and Political Bias in Psychology (pp. 905–927). Berlin Heidelberg: Springer. [doi:10.1007/978-3-031-29148-7_32]
DOUGLAS, H. (2009). Science, Policy, and The Value-Free Ideal. Pittsburgh, PA: University of Pittsburgh Press.
DUNG, P. M. (1995). On the acceptability of arguments and its fundamental role in nonmonotonic reasoning, logic programming and n-person games. Artificial Intelligence, 77(2), 321–357. [doi:10.1016/0004-3702(94)00041-x]
DUPUIS de Tarlé, L., Bonzon, E., & Maudet, N. (2022). Multiagent dynamics of gradual argumentation semantics. Proceedings of the 21st International Conference on Autonomous Agents and Multiagent Systems. [doi:10.1145/3259923]
DUTILH NOVAES, C. (2018). The enduring enigma of reason. Mind & Language, 33(5), 513–524. [doi:10.1111/mila.12174]
FU, G., & Zhang, W. (2016). Opinion formation and bi-polarization with biased assimilation and homophily. Physica A: Statistical Mechanics and Its Applications, 444, 700–712. [doi:10.1016/j.physa.2015.10.006]
GABBRIELLINI, S., & Torroni, P. (2014). A new framework for ABMs based on argumentative reasoning. In B. Kamiński & G. Koloch (Eds.), Advances in social simulation (pp. 25–36). Berlin Heidelberg: Springer. [doi:10.1007/978-3-642-39829-2_3]
GABRIEL, N., & O’Connor, C. (2024). Can confirmation bias improve group learning? Available at: http://philsci-archive.pitt.edu/20528/
GILBERT, N. (1997). A simulation of the structure of academic science. Sociological Research Online, 2(2), 1–15.
HEGSELMANN, R., & Krause, U. (2006). Truth and cognitive division of labor: First steps towards a computer aided social epistemology. Journal of Artificial Societies and Social Simulation, 9(3), 10.
KITCHER, P. (1990). The division of cognitive labour. The Journal of Philosophy, 87(1), 5–22.
KOPECKY, F. (2022). Arguments as drivers of issue polarisation in debates among artificial agents. Journal of Artificial Societies and Social Simulation, 25(1), 4. [doi:10.18564/jasss.4767]
KUHN, T. (2000). The Road Since Structure. Chicago, IL: The University of Chicago Press.
LIU, Q., Zhao, J., & Wang, X. (2015). Multi-agent model of group polarisation with biased assimilation of arguments. IET Control Theory & Applications, 9(3), 485–492. [doi:10.1049/iet-cta.2014.0511]
LONGINO, H. (2002). The Fate of Knowledge. Princeton, NJ: Princeton University Press.
MÄS, M., & Flache, A. (2013). Differentiation without distancing. Explaining bi-polarization of opinions without negative influence. PLoS One, 8(11), e74516.
MERCIER, H. (2017). Confirmation bias - Myside bias. In R. F. Pohl (Ed.), Cognitive Illusions: Intriguing Phenomena in Thinking, Judgment and Memory (pp. 109–124). London: Routledge. [doi:10.4324/9781003154730-7]
MERCIER, H., Bonnier, P., & Trouche, E. (2016). Why don’t people produce better arguments? In L. Macchi, M. Bagassi, & R. Viale (Eds.), Cognitive Unconscious and Human Rationality (p. 205). Cambridge, MA: The MIT Press. [doi:10.7551/mitpress/10100.003.0015]
MERCIER, H., & Heintz, C. (2014). Scientists’ argumentative reasoning. Topoi, 33(2), 513–524. [doi:10.1007/s11245-013-9217-4]
MERCIER, H., & Sperber, D. (2011). Why do humans reason? Arguments for an argumentative theory. Behavioral and Brain Sciences, 34(2), 57–74. [doi:10.1017/s0140525x10000968]
MERCIER, H., & Sperber, D. (2017). The Enigma of Reason. Cambridge, MA: Harvard University Press.
MUTZ, R., Bornmann, L., & Daniel, H. D. (2012). Heterogeneity of inter-Rater reliabilities of grant peer reviews and its determinants: A general estimating equations approach. PLoS One, 7(10), e48509. [doi:10.1371/journal.pone.0048509]
PERA, M. (1994). The Discourses of Science. Chicago, IL: The University of Chicago Press.
PERKINS, D. (2019). Learning to reason: The influence of instruction, prompts and scaffolding, metacognitive knowledge, and general intelligence on informal reasoning about everyday social and political issues. Judgment and Decision Making, 14(6), 624–643. [doi:10.1017/s1930297500005350]
PETERS, U. (2020). Illegitimate values, confirmation bias, and mandevillian cognition in science. The British Journal for the Philosophy of Science, 72(4). [doi:10.1093/bjps/axy079]
POPPER, K. R. (1962). Conjectures and Refutations: The Growth of Scientific Knowledge. London: Routledge.
PROIETTI, C., & Chiarella, D. (2023). The role of argument strength and informational biases in polarization and bi-polarization effects. Journal of Artificial Societies and Social Simulation, 26(2), 5. [doi:10.18564/jasss.5062]
RESCHER, N. (2007). Dialectics. Berlin: De Gruyter.
SINGER, D. J., Bramson, A. L., Grim, P., Holman, B., Jung, J., Kovaka, K., Ranginani, A., & Berger, W. J. (2018). Rational social and political polarization. Philosophical Studies, 176, 2243–2267. [doi:10.1007/s11098-018-1124-5]
SMART, P. R. (2018). Mandevillian intelligence. Synthese, 195(9), 4169–4200. [doi:10.1007/s11229-017-1414-z]
STANOVICH, K. E., & West, R. F. (2007). Natural myside bias is independent of cognitive ability. Thinking & Reasoning, 13(3), 225–247. [doi:10.1080/13546780600780796]
STANOVICH, K. E., West, R. F., & Toplak, M. E. (2013). Myside bias, rational thinking, and intelligence. Current Directions in Psychological Science, 22(4), 259–264. [doi:10.1177/0963721413480174]
ŠEŠELJA, D., & Straßer, C. (2013). Abstract argumentation and explanation applied to scientific debates. Synthese, 190, 2195–2217.
ŠEŠELJA, D., & Weber, E. (2012). Rationality and irrationality in the history of continental drift: Was the hypothesis of continental drift worthy of pursuit? Studies in History and Philosophy of Science, 43, 147–159.
TAILLANDIER, P., Salliou, N., & Thomopoulos, R. (2021). Introducing the argumentation framework within agent-Based models to better simulate agents’ cognition in opinion dynamics: Application to vegetarian diet diffusion. Journal of Artificial Societies and Social Simulation, 24(2), 6. [doi:10.18564/jasss.4531]
WOLFE, C. R., & Britt, M. A. (2008). The locus of the myside bias in written argumentation. Thinking & Reasoning, 14(1), 1–27. [doi:10.1080/13546780701527674]
ZAMORA BONILLA, J. (1999). The elementary economics of scientific consensus. Theoria: An International Journal for Theory, History and Foundations of Science, 461–488.
ZOLLMAN, K. (2011). Computer simulation and emergent reliability in science. Journal of Artificial Societies and Social Simulation, 14(4), 15. [doi:10.18564/jasss.1861]
ZOLLMAN, K. J. S. (2007). The communication structure of epistemic communities. Philosophy of Science, 74(5), 574–587. [doi:10.1086/525605]