An Agent-Based Model to Assess Possible Interventions for Large Shigellosis Outbreaks

, , , , , ,
and
aSchool of Global Public Health, New York University, United States; bDivision of Disease Control, New York City Department of Health and Mental Hygiene, United States
Journal of Artificial
Societies and Social Simulation 27 (3) 2
<https://www.jasss.org/27/3/2.html>
DOI: 10.18564/jasss.5384
Received: 27-Sep-2023 Accepted: 23-Apr-2024 Published: 30-Jun-2024
Abstract
Large outbreaks of Shigella sonnei among children in Haredi Jewish (ultra-Orthodox) communities in Brooklyn, New York have occurred every 3–5 years since at least the mid-1980s. These outbreaks are partially attributable to large numbers of young children in these communities, with transmission highest in child care and school settings, and secondary transmission within households. As these outbreaks have been prolonged and difficult to control, we developed an agent-based model of shigellosis transmission among children in these communities to support New York City Department of Health and Mental Hygiene staff. Simulated children were assigned an initial susceptible, infectious, or recovered (immune) status and interacted and moved between their home, child care program or school, and a community site. We calibrated the model according to observed case counts as reported to the health department. Our goal was to better understand the efficacy of existing interventions and whether limited outreach resources could be focused more effectively. We evaluated how well disseminating hand washing education in child care programs can reduce the number of infected children. The model indicated that intervention efficacy may be as high as 24% when all intervention parameters are at optimal values but only approximately 7% for a more realistic, less stringent scenario. We ranked intervention parameters according to their permutation importance using a random-forest regression analysis. The most important parameter was the minimum number of reported cases in a child care program that triggers a visit to disseminate hand washing education, followed by the use of non-antibacterial soap in hand washing education, the number of additional visits to child care programs, and the probability of successfully obtaining information on child care program attendance via patient interview. Additional strategies should be considered, such as working with community partners to assist with hand hygiene education at facilities during an outbreak.Introduction
Shigellosis is an infectious disease with symptoms such as diarrhea, fever, and abdominal cramps (Parthasarathy 2013). Shigella bacteria are easily transmitted due to a low infectious dose via person-to-person contact and fomites (i.e., by touching door handles, cups, utensils, toys, etc.). Children who are <5 years old are most often affected since they tend to be less adherent to hand hygiene practices and lack immunity from prior exposure to Shigella bacteria. Interventions to reduce transmission include improved hand hygiene and isolation of infected individuals. While promising avenues of vaccine development are being pursued, no vaccine is currently available (Herrera et al. 2022). In wealthier countries, while not fatal, shigellosis is a leading cause of diarrheal outbreaks in child care centers (Lampel & Sandlin 2003). Young children are also more likely to become dehydrated during illness (Parthasarathy 2013). In the U.S., the most common Shigella species is Shigella sonnei (CDC 2020).
Among acute gastrointestinal illness outbreaks transmitted person-to-person or via environmental contamination in the U.S., shigellosis outbreaks are relatively rare (CDC 2023; Wikswo et al. 2015). U.S. outbreaks have previously occurred among men who have sex with men (Bowen et al. 2015; CDC 2001; Hines et al. 2016), persons experiencing homelessness (Hines et al. 2016), and young children (Aluko et al. 2022; Mattison et al. 2022). Additionally, shigellosis outbreaks have recurred in Haredi Jewish (ultra-Orthodox) communities in North America, Europe, and Israel (Cohen et al. 2019; De Schrijver et al. 2011; Garrett et al. 2006; Rew et al. 2018; Sobel et al. 1998). Haredi Jews tend to live in highly observant religious enclaves in major metropolitan areas worldwide (Alfasi et al. 2013), including New York City (NYC). These communities and neighborhoods have collective familial and social structures, characterized by communal prayer and religious study as well as shared life cycle events and holiday celebrations, and community members are frequently part of large extended families (Pirutinsky et al. 2020). While these characteristics ensure that Haredi communities are tight-knit, they also partly help explain why these communities are more susceptible to large, fast-growing, person-to-person shigellosis outbreaks. In NYC, outbreaks in Haredi communities are recurrent, prolonged, and start at different times of the year. Among Haredi communities in Brooklyn, outbreaks have been noted since the 1980s, occurring every 3–5 years.
When shigellosis outbreaks occur, the NYC Department of Health and Mental Hygiene (NYC Health Department) conducts case investigations to determine child care attendance and perform child care exclusions; visits child care programs, WIC programs, and yeshivas (religious educational institutions) with young children to distribute hand hygiene and diapering posters and to conduct hand hygiene education; conducts outreach through community media; meets with yeshiva directors; and issues health alerts and makes calls to community healthcare providers. Despite these efforts, epidemiologists at the NYC Health Department considered the recurrent outbreaks to be difficult to control in real-time. We wished to better understand the theoretical efficacy of existing interventions, and whether they could be modified, within practical constraints, to more effectively focus limited outreach resources. In this paper, we present an agent-based model to simulate a single acute shigellosis outbreak among the Haredi communities of Brooklyn and study how interventions could be optimized to limit the outbreak. Real-world data from past NYC Health Department responses to outbreaks in these communities were used for model inputs to understand the impact of various possible interventions to control ongoing disease transmission.
Background
Most studies of the spread of shigellosis use compartmental models, which divide the population into categories such as Susceptible, Exposed, Infectious, and Recovered. Chaturvedi et al. (2014) developed a Susceptible-Infectious-Recovered-Susceptible model with births and deaths that are unrelated to the disease and loss of immunity over time. Edward et al. (2020a) and Edward et al. (2020b) developed a model that included a compartment for Carriers (asymptomatic individuals) and a reservoir of the bacteria in the environment. Chen et al. (2014) developed a Susceptible-Infectious-Recovered-Water model for the spread of Shigella in rural China, which included transmission between water and persons by adding a compartment for the concentration of the bacteria in water. They showed that combining water disinfection, school closure, isolation, and antibiotic treatment could lower the total attack rate. Zhao et al. (2022) have studied the seasonality of shigellosis outbreaks in regions of China using logistic and compartmental models that include asymptomatic persons and water reservoirs.
Joh et al. (2013) estimated the basic reproduction numbers and reporting proportions for U.S. counties during 1967–2007 using a time series Susceptible-Infectious-Recovered model. Their estimation of the reporting rates suggests that the number of infections may be more than ten times the number of laboratory-confirmed cases and that the estimated basic reproduction number (\(R_{0}\)) in most jurisdictions was under 1.5.
Agent-based modeling is a computational alternative to compartmental models that allows a better representation of heterogeneous populations and realistic contact patterns without the benefits of mathematical tractability. There are few agent-based models of shigellosis transmission. Glushchenko et al. (2019) used an agent-based model for studying the development of antibiotic resistance in community and hospital settings and applied the model to Shigella spp. Shridhar et al. (2022) used empirical social network and socio-centric data for 176 villages in Honduras to construct an agent-based model that simulated the spread of Shigella and influenza virus. They used the model to evaluate individuals’ susceptibility to infection and their spreading capability.
Our aim was to evaluate the effectiveness of potential NYC Health Department interventions in reducing the number of infections during shigellosis outbreaks in Haredi communities. This aim confines us to a specific setting that requires a new model. We thus developed an agent-based model representing an artificial community with the elements that are required to simulate our interventions, such as child care programs and schools where children may infect one another. We focus on acute outbreaks that start after a single infectious agent is introduced to the community and end once no agent is infectious. We used real-world NYC Health Department data to construct a detailed simulation of potential interventions, including disseminating hand washing education and excluding children from child care programs while infectious.
The rest of the paper has the following structure: In Section 3, we describe the model, while in Section 4 we describe how we incorporated and evaluated interventions. The paper concludes with a discussion (Section 5).
Model Description
Defining the study area
To model shigellosis outbreaks, it is necessary to define the geographic area where outbreaks occur while excluding areas with no cases. This allows the estimation of various quantities, such as the number of reported cases and the number of agents that we need to represent in our model. For this purpose, we identified the census tracts where the Haredi population resided and validated that the outbreaks occurred within the selected areas.
To define a geographic area as a proxy for the Haredi population, we used the 2015 American Community Survey (U.S. Census Bureau) data to calculate the proportion of residents \(\geq 5\) years old who spoke Yiddish or Hebrew at home in each of the census tracts of Brooklyn. We selected tracts where at least 18% of residents were Yiddish or Hebrew speakers. We found that this threshold corresponds well to three distinct neighborhoods in Brooklyn where recurrent Shigella sonnei outbreaks among the Haredi population have been observed. Reportable disease data collected by the NYC Health Department indicate that 92% of the selected tracts had at least one shigellosis case among children \(< 12\) years old diagnosed during the 2014–2015 outbreak period. Thus, this subset of tracts seems to include the populations that were exposed to shigellosis outbreaks. See the Appendix for additional information.
Agents
Our agent-based model was implemented in NetLogo 6.3.0 (Wilensky 1999). Agents represent children \(< 12\) years old. Even though each agent has a specific age that is represented by a real number, we focused on two age groups: younger children <5 years old (i.e., \([0,5)\)) and older children between the ages of 5 and \(< 12\) years old (i.e., \([5,12)\)). The model does not contain individuals \(\geq 12\) years old because they are not considered an important contributor to the spread of shigellosis as they tend to practice effective hygiene habits that reduce their susceptibility and tendency to spread the pathogen.
Each agent has an infection status, which characterizes its state in relation to the pathogen. An agent can be in one of four states: (1) an agent in the susceptible state has no specific immunity to Shigella sonnei and may get infected, (2) an exposed agent has recently been infected but is not yet infectious, (3) an infectious agent may transmit the pathogen to others, and (4) a recovered agent was infected in the past and recovered. Recovered agents gain immunity to shigellosis, and thus they cannot be reinfected during the outbreak period. According to this scheme, an infectious agent can transmit the pathogen to a susceptible agent. The infected individual becomes exposed for a short duration of time until the pre-infectious period ends and the agent becomes infectious. Once the infectious period ends, the agent recovers. In the simulation, we assumed that once recovered, an agent will stay recovered until the simulation ends.
The agents interact within four types of mixing areas: households, child care programs, schools, and community sites. Younger agents (\(< 5\) years old) tend to go to child care programs while older agents (\(5-<12\) years old) go to school. According to Garrett et al. (2006), by the age of two years, 90% of children are enrolled at a child care program. We assumed that younger children begin to join child care programs at the age of six weeks and at a constant rate that leads to 90% enrollment by the age of two years. All older agents are enrolled in school.
Initial conditions and settings
Space is represented as a square lattice of 51 by 51 cells. Each household, child care program, and school is equally likely to be located at each of the 2601 cells (Figure 1). For each household, the model assigns the closest child care program and school. When two or more child care programs or schools have the same minimal distance, the model chooses one of them at random. We consider community sites to be non-spatial entities. A random community site is chosen for each household regardless of distance. Community sites serve as general mixing areas for the study area. We assumed that agents go to community sites on the weekends to meet community members, family, and friends. Thus, community sites allow the pathogen to spread non-spatially (i.e., it allows the pathogen to jump from one area to another).
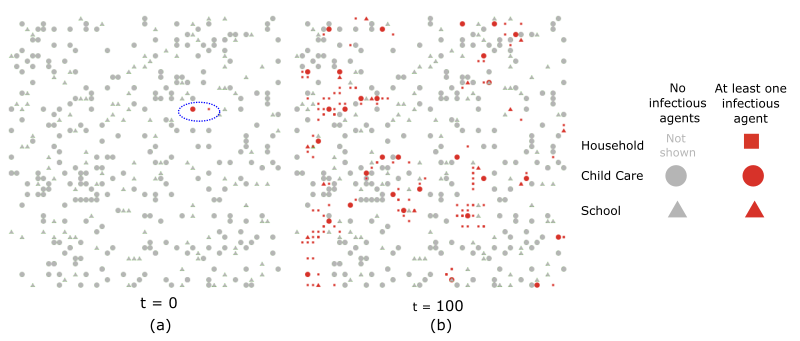
The model includes 289 child care programs, 144 schools, and 453 community sites. Based on the number of births in the study area, we set the number of agents in each age group as 3,141.6, resulting in 15,708 younger (\(< 5\) year-olds) and 21,991 older (\(5-<12\) year-olds) agents. These estimates are based on NYC Health Department data and resources maintained by the community. See the Appendix for additional information.
The initial percentage of agents that have an infection status of recovered (children with immunity) is an important parameter. Recovered persons tend to reduce the spread of pathogens by disrupting chains of transmission (herd immunity). We estimated the initial proportion of recovered agents by considering past outbreaks. As shigellosis outbreaks recur in many Haredi communities every few years, children tend to gain immunity by being exposed to the pathogen during one of the outbreaks. As older children are likely to be exposed to more outbreaks compared with younger children, the proportion of susceptible persons may decrease with age. However, the protection may be temporary, as individuals may lose their specific immunity. Based on NYC Health Department data on reported cases, we estimated the proportion of recovered persons for each of the two age groups (younger and older). Our approach is described in the Appendix. According to our estimation, approximately 7% of younger and 53% of older agents have immunity to Shigella as of the start of an outbreak period. These agents are assigned an infection state of recovered (i.e., immune) at time 0.
We had no information about when an index case was introduced to the community or whether two or more infectious persons entered at the same time. Accordingly, we took a conservative approach and began each simulation with a single infectious agent within the community. The agent is selected at random from the set of susceptible agents. In addition, our model does not include any importations of infected persons from outside the community, though it is important to note that there are likely importations of infected persons given travel between communities within the U.S. and abroad.
Model evolution
Time progresses in discrete steps of single days. During each day, agents move among the mixing areas and may be infected with the pathogen. Every agent visits the mixing areas that are assigned to its household. We assumed that agents visit child care programs and schools five days a week, while on the two weekend days they visit community sites.
During a weekday, an older agent mixes in the household and school. Younger agents enrolled in child care mix in the household and child care program, while younger agents not enrolled in child care stay in the household. During the weekend, all agents visit the community site assigned to their household.
An agent who is infected with Shigella enters the exposed (pre-infectious) state. The exposed period lasts for approximately two days on average (CDC 2020). When the pre-infectious period ends, the agent becomes infectious for an average period of seven days (Joh et al. 2013; Niyogi 2005; Shridhar et al. 2022). At each time step, an exposed agent has a probability of \(\frac{1}{2}\) of becoming infectious while an infectious agent has a probability of \(\frac{1}{7}\) to recover. Thus, this process leads to a geometric distribution of time periods with the given expected values (two and seven days).
The infectious period implies that 99% of the agents will recover within 30 days. This percentage is consistent with the Control of Communicable Diseases Manual (Heymann 2008), which indicates infectious bacteria are usually no longer present in feces within four weeks after illness. If future studies yield better distribution estimations, such estimations could be easily incorporated into the model.
Transmission
We defined three free parameters representing the transmission probabilities between individuals:
- The effective contact probability for households (\(p_{home}\)).
- The effective contact probability for child care programs and schools (\(p_{education}\)).
- The effective contact probability for community sites (\(p_{community}\)).
An effective contact is a contact between two individuals that leads to transmission (Vynnycky & White 2010). The effective contact probabilities represent two random processes: the probability that an agent will have contact with another agent in the mixing area and the probability that such contact (if it occurred) will lead to transmission assuming that one agent is susceptible and the other is infectious. All the probabilities represent the transmission chance per visit.
For example, let us assume that one agent is infectious in a mixing area (e.g., a child care program), and nine are susceptible. Let us further assume that this infectious agent tends to have contact with 50% of the agents per visit (i.e., the agent has a 50% probability of meeting each of the other agents in the mixing area). Thus, the agent is expected to contact 4.5 susceptible agents on average per visit. However, not all contacts will lead to transmission; if we assume that the probability of transmission per contact is 0.25, then on average, the agent will infect approximately \(4.5 \times 0.25 = 1.1\) agents per visit in that mixing area. In this scenario, the effective contact probability is \(0.5 \times 0.25 = 0.125\). Therefore, every susceptible agent has a probability of 0.125 of being infected. The example assumes that only a single agent is infectious, but we can extend this approach to multiple infectious agents within a mixing area.
We assumed that older children have a lower chance of being infected or transmitting the bacteria because of improved hygiene and a lower number of contacts. We represent this tendency by introducing the relative risk parameter \(r\). We used the parameter to lower the effective contact probabilities of older children. For each of the three effective probabilities \(p \in \{p_{home}, p_{education}, p_{community}\}\), we used the following probabilities of effective contacts between pairs of younger and older agents in a mixing place (Table 1).
| To Younger | To Older | |
|---|---|---|
| From Younger | \(p\) | \(r \times p\) |
| From Older | \(r \times p\) | \(r \times p\) |
We assumed all the agents of the same age group (younger and older) have the same probability of being infected within a mixing area. Note that this mechanism reduces the effective contact probability of schools to \(r \times p_{education}\) because all the agents in schools are older. It also affects the transmission in community sites which include younger and older agents.
At each place, the probability that a susceptible agent will be infected per visit (the force of infection \(\lambda\)) is calculated using the Reed–Frost equation (Vynnycky & White 2010):
| \[ \lambda_{Y} = 1 - (1 - p)^{I_{Y}}(1 - r \times p)^{I_{O}}\] | \[(1)\] |
| \[ \lambda_{O} = 1 - (1 - r \times p)^{I_{Y} + I_{O}}\] | \[(2)\] |
Demographics
Even though the focus of the current work is on simulating a single acute outbreak during a period in which the population structure remains relatively constant, the model includes basic demographic processes. The age of agents is updated at each time step. Agents that reach the age of 12 years are replaced by susceptible newborn agents (thus maintaining a constant population size), and younger agents that reach the age of five move to school on a single random day of the year representing the beginning of the school year. This approach, which preserves the total number of agents, is analogous to how many compartmental models maintain a constant population size by equating the rates of people who exit and enter the system. We assumed that no recovered agent loses immunity during the simulation.
Calibration
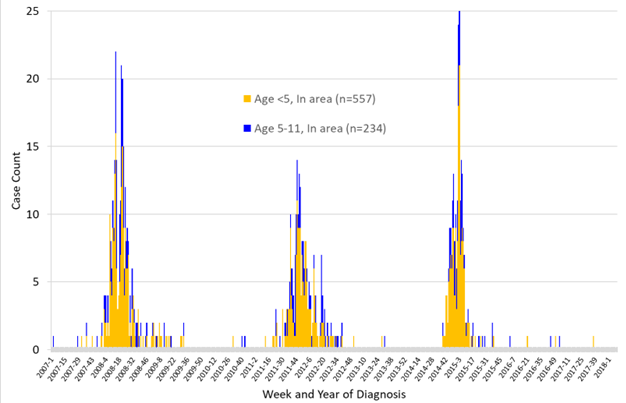
The model includes four parameters that needed to be estimated: three effective contact probabilities (\(p_{home}\), \(p_{education}\), and \(p_{community}\)) and the relative risk \(r\). These parameters determine the shape of the epidemic curve. To make the model representative of shigellosis outbreaks, we calibrated these parameters according to empirical counts of reported cases of younger and older children. We constructed a time series of reported cases that occurred within the study area by counting cases of younger and older children separately. Our time series contains three outbreaks during 2007-2017 (Figure 2). We focused our attention on the outbreak that occurred during October 2014-August 2015 because it was an abrupt outbreak and, therefore, highly challenging from the perspective of conducting successful public health interventions. Calibrating the model for other outbreaks may lead to somewhat different parameter estimations. Our base model incorporates no interventions that may have reduced the spread of the pathogen during the event. Thus, the parameter estimations would “absorb” the potential reduction in the spread. We assumed based on first-hand knowledge of working with this community that the efficacies of past interventions were limited. This assumption is supported by our intervention analysis.
The counts within each week are relatively small because of the low proportion of infections ascertained as cases and the population size of the study area. As a result, the data are noisy. To mitigate this issue, we aggregated the data into bins of two weeks and ran a (central) moving average on the binned data with a window size of 3 (i.e., \(s_{i} = \frac{a_{i-1} + a_{i} + a_{i + 1}}{3}\)), which reduced the noise in the counts.
The NYC Health Department is only notified of the subset of Shigella infections that are reported by healthcare providers or laboratories. Thus, the number of infections that the model produces needs to be converted to reported cases. Because shigellosis can be a mild, self-limited illness, many parents might choose not to take their children to the doctor or take only a single child within the household. According to Scallan et al. (2011), \(\frac{1}{33.3}\) shigellosis cases are reported. Similar estimations of either 1% or 6% were obtained by Joh et al. (2013). We adopted the Scallan et al. (2011) estimation and transformed the model-produced infections into reported cases by dividing the number of infected agents by 33.3.
Each simulation begins with a single infectious agent and ends once no agent is exposed or infectious (i.e., pathogen extinction has occurred). Our model includes chance events, which lead to different results when the same parameter values are used. As we start with a single infectious agent, such random events may lead to early pathogen extinction in specific realizations, while in other realizations, the pathogen may spread and cause a major outbreak (Britton 2010). Extinction may occur even when the basic reproduction number is above 1. Figure 3 shows the distribution of outbreak sizes for the calibrated parameters. We see that two types of outcomes exist: simulations in which early extinction occurred and simulations in which a major outbreak occurred. It is also clear that it is straightforward to distinguish between these two types.
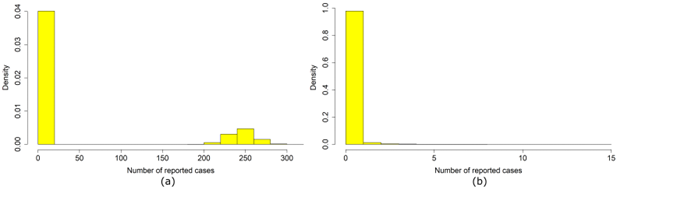
Any outbreak that was observed in reality was the result of a successful spread of the pathogen. Thus, to compare our model correctly with empirical data, we only considered realizations that led to an outbreak. For each model run, we made 50 attempts to produce a major outbreak and logged the first successful trial. If no major outbreak occurred after 50 trials, we logged the last trial. We considered a major outbreak when \(> 16\) reported cases occurred. The three observed outbreaks during 2007-2017 each had case counts an order of magnitude larger than this threshold.
We ran the model multiple times for each set of parameters to construct an average time series of reported cases. In certain simulations, the pathogen may start to spread in the community quite early, while in others, it might spread slowly for a while, with a small number of reported cases for a period before substantial spreading begins. Therefore, two simulations might have similar time series in which one is shifted in time compared with the other. From our perspective, such simulations are similar, as we do not know when the pathogen was introduced to the study area. Before averaging the counts, we shifted the time series so each outbreak began roughly at the same time. This time translation allowed us to reduce variability related to the time it takes the pathogen to start spreading. We achieved reduced variability by labeling the earliest time-bin that included \(> 5\) reported cases as time 0. The time-shifted series of all the repetitions of each parameter were then aggregated to produce the average time series.
We employed a simple Approximate Bayesian computation (ABC) scheme (Toni et al. 2009) for inferring credible intervals of the parameters. We first defined a parameter space that represents the prior distribution of the parameters. We used the most straightforward ABC rejection sampling procedure, which requires estimating the error between the model and the empirical data. The error was calculated using the observed and model-generated counts of younger and older cases. We compared the averaged time series of each parameter set with the empirical counts using the sum of squares differences:
| \[ D=\sqrt{\sum_{i}(Y_{D}(i) - Y_{M}(i))^{2} + \sum_{i}(O_{D}(i) - O_{M}(i))^{2}}\] | \[(3)\] |
- \(Y_{D}(i)\) is the empirical number of reported cases among younger children (\([0, 5)\) years) in the data at time bin \(i\);
- \(Y_{M}(i)\) is the average number of reported cases among younger agents (\([0, 5)\) years) produced by the model at time bin \(i\);
- \(O_{D}(i)\) is the empirical number of reported cases among older children (\([5, 12)\) years) in the data at time bin \(i\);
- \(O_{M}(i)\) is the average number of reported cases among older agents (\([5, 12)\) years) produced by the model at time bin \(i\).
We used the sum of squares errors rather than the average because the length of the observed and simulated time series may be different. For example, the model may produce an outbreak with a long tail consisting of a low number of infections for a period during which no cases were observed in reality. The sum would accumulate these errors and penalize the model for the long tail while an average error could decrease when the model produces a long tail.
Our search space was four-dimensional (Table 2). We constructed the parameter intervals by manual experimentation. We reduced the parameter space by assuming that the effective contact probability in child care and school settings was equal to or larger than the one of community sites (\(p_{education} \geq p_{community}\)), representing the closer interactions in child care programs and schools.
| Parameter | Sampled values |
|---|---|
| \(p_{house}\) | [0.02, 0.07] with a step of 0.0025 |
| \(p_{education}\) | [0.002, 0.007] with a step of 0.0025 |
| \(p_{community}\) | [0.002, 0.007] with a step of 0.0025 for values below or equal to \(p_{education}\) |
| \(r\) | [0.1, 0.6] with a step of 0.025 |
The parameters were estimated in two steps.
In step 1, we conducted a crude estimation of the accepted area. We sampled each combination 50 times and produced an average infection curve for each. We then identified the region of small errors by accepting all the combinations that led to an error below 15 children (\(D < 15\)).
In step 2, we refined our estimation of the accepted area by decreasing the step size of each of the four parameters by half and sampling each combination 125 times. We accepted combinations that resulted in an error smaller than 12 children (\(D < 12\)).
Based on the accepted areas, we took the average of each parameter as our estimation and constructed the credible intervals (CI) by calculating the 2.5% and 97.5% percentiles (Table 3).
| Parameter | Description | Estimate (95% CI) |
|---|---|---|
| \(p_{home}\) | Effective contact probability in households | 0.03653 (0.02125, 0.06500) |
| \(p_{education}\) | Effective contact probability in child care programs and schools | 0.00359 (0.00300, 0.00425) |
| \(p_{community}\) | Effective contact probability in community sites | 0.00315 (0.00250, 0.00363) |
| \(r\) | Older children relative risk coefficient | 0.31524 (0.26250, 0.36250) |
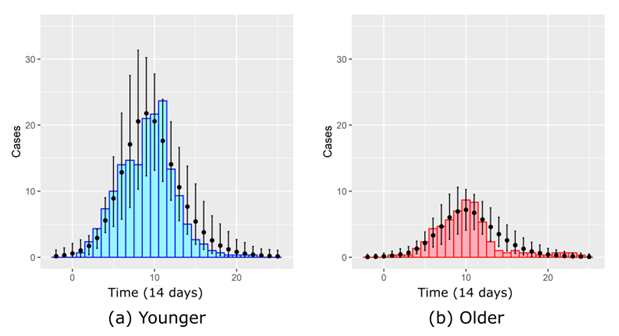
The average number of infections produced by the model for the selected parameters with the smoothed empirical counts is shown in Figure 4. The model counts are based on 1,000 simulated outbreaks. We see good qualitative correspondence even though the model tends to overestimate the number of cases after the peak. See the Appendix for estimations of the net and basic reproduction numbers. In the next section, we will use the parameterized model to study the efficacy of interventions.
Interventions Evaluation
Modeling interventions
The calibrated model can be used to estimate the effectiveness of interventions. In this study, we focused on interventions that can be taken by the NYC Health Department during an outbreak, including teams that visit child care programs and disseminate hand hygiene education. A meta-analysis has demonstrated that community-based hand hygiene education has a strong protective effect against gastrointestinal illnesses (RR: 0.69; 95% CI: 0.50, 0.95) and has a stronger effect when a non-antibacterial soap is used (RR: 0.61; 95% CI: 0.43, 0.88) (Aiello et al. 2008). Thus, we investigated how the adoption of handwashing practices initiated by hand hygiene education may reduce the number of infections. In addition, the NYC Health Code requires the NYC Health Department, regardless of whether an outbreak is ongoing, to temporarily exclude (keep from attendance) reported infectious children from child care programs.
In the model, each child care program is labeled as either visited or unvisited by a team. This label indicates whether hand hygiene education was disseminated. When a simulation begins, all child care programs are marked as unvisited, and during a simulation, a child care program can only be visited once. When a child care program is visited, the transmissibility of the pathogen within the child care program is reduced. We parameterized this reduction using the two estimations of the relative risk of hand hygiene education mentioned above. We incorporated the uncertainty in the relative risk estimation as follows: at the beginning of each simulation, we draw a relative risk from a log-normal distribution with mean \(rr_{mean}\) and standard deviation of \(rr_{std}\) (Altman 1991). \(rr_{std}\) is calculated using the published confidence intervals shown above (Aiello et al. 2008), assuming that the sampling distribution of relative risks logarithm is approximately normal. The sampled relative risk is upper-bounded by 1.
The interventions are modeled in six steps: (1) simulating reporting, (2) scheduling interviews, (3) conducting interviews, (4) simulating exclusions, (5) scheduling visits to child care programs, and (6) conducting visits to child care programs.
Step 1: Simulating reporting
Shigellosis cases are individually reportable by healthcare providers and laboratories (New York City Health Code Article 11). Among patients who are reported to the NYC Health Department, there is a delay between the illness onset date (which is obtained from the patient interview if the case is assigned for investigation) and the date the health department is first notified (typically by electronic laboratory reporting). This delay accounts for medical care-seeking, specimen submission, laboratory testing, and reporting. To quantify this delay between illness onset and reporting, we constructed the empirical distribution of delays based on 216 shigellosis cases among \(< 12\) year-old NYC residents (Figure 5a). We found that notification to the NYC Health Department occurred within five days of illness onset for 48% of cases, within nine days of illness onset for 81% of cases, and within 21 days of illness onset for 95% of cases. In the model, we assumed that the time of illness onset coincides with the moment an agent becomes infectious. An agent that acquires the infectious state has a probability of \(p_{report} = \frac{1}{33.3}\) to be reported (Scallan et al. 2011). If an agent is reported, a future time of notification is scheduled by sampling a random lag from the distribution. No action will be taken by the health department model regarding that agent until the notification time is reached.
Step 2: Scheduling interviews
NYC Health Department staff investigate a subset of notified shigellosis cases, whereby they attempt to interview patients or their caregivers by telephone to collect key information, including illness onset date and whether the patient attends a child care program. In the model, we defined \(p_{success}\) as the probability that a reported case is assigned for investigation and that the interview is successfully completed and all needed information for public health action is collected. The probability was estimated based on 121 <5 year-olds linked to the 2018–2019 shigellosis outbreak, of whom 57 (47%) were completely investigated. To evaluate the benefit of higher success probabilities, we considered additional values of \(p_{success}\) (see Table 5).
Among cases that are investigated, there is a delay between the date the NYC Health Department is first notified, and the date the patient interview is completed. These delays are related to staff workloads, patient accessibility, and the practice of conducting interviews only on weekdays. We quantified the distribution of these delays based on 107 shigellosis patients of any age linked to the 2018-2019 outbreak whose cases were completely investigated (Figure 5b). We found that interviews were conducted within seven weekdays of notification for 60% of cases, within 14 weekdays of notification for 82% of cases, and within 24 weekdays of notification for 96% of cases. In the model, the future times of interviews are scheduled by sampling a random lag from the distribution. As the NYC Health Department does not conduct interviews on Saturdays and Sundays, these days are skipped.

Step 3: Conducting interviews
Interviews are simulated on the scheduled day by tagging the reported agent as “interviewed.”
Step 4: Simulating exclusions
If a shigellosis patient is \(< 5\) years old and determined upon investigation to attend a child care program, then the NYC Health Code requires the NYC Health Department to exclude the patient from child care until the patient is no longer a risk to others based on submission of two consecutive negative stool samples (NYC Health Code Article 11.15, Carias et al. 2019). NYC Health Department staff suspect that patients are nearly always compliant with exclusion orders but are aware of occasional instances when excluded children prematurely return to child care, though this is not tracked systematically. In the model, if a younger agent enrolled in child care is still infectious at the time of the interview, the agent has a probability \(p_{compliance}\) to be excluded from the child care program (see Table 5 for investigated values). \(p_{compliance}\) represents the probability that the caregiver will comply with the NYC Health Department exclusion order. An excluded agent stays at the household during the exclusion period while other agents go to school or child care and return and mix in the household. The agent may stay at home with other young siblings who do not attend child care (unenrolled or other excluded siblings). The agent goes back to the child care program once recovered.
Step 5: Scheduling visits to child care programs
A majority of child care programs historically have consented to allow NYC Health Department staff to conduct hand hygiene education within a few days of the request based on logistical feasibility, but informal experience suggests that approximately 20% of facilities in this community decline the intervention. When the model is initialized, all child care programs are tagged as either cooperative or uncooperative. We use the parameter \(p_{coop}\) to represent the probability that a child care program will be cooperative. We consider \(p_{coop}\) to represent the cooperation probability after multiple attempts by health department staff. Thus, a child care program that refuses to cooperate (with probability \(1 - p_{coop}\)) is not visited during the simulation.
Successful interviews allow the health department to monitor the number of children reported with shigellosis within each child care program. In the model, we defined \(c_{childcare}\) as the number of interviewed children in a child care program that would lead to the scheduling of a visit for the dissemination of hand hygiene education at that child care program. Only child care programs that were neither previously visited during the outbreak period nor scheduled for a visit are considered. Once \(c_{childcare}\) or more interviewed children are identified in a child care program, the modeled NYC Health Department attempts to schedule a visit to that child care program. The time lag between the identification and the scheduled visit is sampled from an exponential distribution with a mean of \(m_{lag}\) days. Child care program visits are conducted on weekdays. We denote \(v_{daily}\) as the highest number of visits that can be conducted in a single day. If the sampled date is full, the visit is scheduled on the next available weekday (i.e., a weekday with less than \(v_{daily}\) scheduled visits). Note that the actual average time lag may be longer than \(m_{lag}\) when many visits are scheduled.
After scheduling a visit to all qualified child care programs each day, up to \(n_{extra}\) additional randomly selected child care programs are scheduled for a visit. The extra child care programs do not include any programs that had already been scheduled or visited, any uncooperative programs, nor any programs with less than \(n_{enrolled}\) enrolled children. The \(n_{enrolled}\) threshold ensures that smaller child care programs are not included in the additional visits. No more than \(v_{daily}\) visits can be scheduled per day. If possible, some or all the extra programs are scheduled for the same day as the program(s) that triggered the visit. Otherwise, they are scheduled on the next available day.
These extra child care programs are sorted by size; a program with many agents is visited earlier than one with few agents.
Step 6: Conducting visits to child care programs
Visits to child care programs are simulated on the scheduled day by tagging the child care program as “visited.” From that moment on, the effective contact probability used for the visited program is the product of \(p_{education}\) and the sampled relative risk.
Sampling the intervention space
The interventions are characterized using the nine parameters described above: \(rr_{mean}\), \(v_{daily}\), \(p_{coop}\), \(m_{lag}\), \(c_{childcare}\), \(n_{extra}\), \(p_{success}\), \(p_{compliance}\) and \(n_{enrolled}\) with the values presented in the Appendix (Table 5). We calculated all 17,280 combinations of parameter sets. Each set of the parameter combination was executed 1,000 times.
Analysis of interventions
The proportion of major outbreaks
Because the model begins with a single infectious agent, not all runs produce a major outbreak (when \(> 16\) reported cases have occurred) even though the reproduction number is above 1. All evaluated interventions began once one or more infected agents were detected in a child care program. Such detection is most likely to occur once a major outbreak has already started. For this reason, we did not expect any of our interventions to reduce the proportion of major outbreaks in the simulations. See the Appendix for a description of the statistical test for this hypothesis.
Evaluating intervention efficacy
The strictest intervention that we examined is based on the following parameters:
- A 100% success of interviews to ascertain child care attendance among reported cases (\(p_{success} = 1\))
- Full compliance by caregivers to temporarily exclude infectious children from child care programs (\(p_{compliance} = 1\))
- Minimum number of successfully interviewed cases in a child care program that triggers a visit threshold of 1 (\(c_{childcare} = 1\))
- Full cooperation by child care programs to participate in a hand hygiene education visit (\(p_{coop} = 1\))
- An average of one weekday lag between successful interview of a reported case attending a child care program and a scheduled program visit (\(m_{lag} = 1\))
- Maximum of four child care program visits per weekday (\(v_{daily} = 4\))
- An expected protective effect of hand hygiene education when non-antibacterial soap is used of \(rr_{mean} = 0.61\) (\(rr_{std} = 0.178\))
- Minimum child care program size threshold of 34 children for extra visits (\(n_{enrolled} = 34\))
- Six extra child care program visits scheduled per day (\(n_{extra} = 6\)).
These parameters led to an average efficacy of 23.8% (95% CI: 0.22, 0.25). In other words, the intervention reduced the total number of infections by 23.8%.
We can explore a less stringent scenario with a lower protective effect of hand hygiene education, lower cooperation probability of child care programs and caregivers, and longer delays (the three other parameters are the same as before):
- A 47% success of interviews to ascertain child care attendance among reported cases (\(p_{success} = 0.47\))
- 95% compliance by caregivers to temporarily exclude infectious children from child care programs (\(p_{compliance} = 0.95\))
- A probability of 80% cooperation by child care programs to participate in a hand hygiene education visit (\(p_{coop} = 0.8\))
- An average of two weekdays’ lag between successful interview of a reported case attending a child care program and a scheduled program visit (\(m_{lag} = 2\))
- An expected protective effect of hand hygiene education when non-antibacterial soap is not used of \(rr_{mean} = 0.69\) (\(rr_{std} = 0.163\))
- Minimum child care program size threshold of 40 children for extra visits (\(n_{enrolled} = 40\))
- Two extra child care program visits scheduled per day (\(n_{extra} = 2\))
This parameter set led to a lower average efficacy of 6.5% (95% CI: 0.053, 0.077).
It is reasonable to hypothesize that some of the parameters are more important than others in reducing the pathogen’s spread. To estimate the permutation importance of each of these parameters, we fit a random-forest regression (Wright et al. 2016). The total number of infections was used as the outcome variable, while the intervention parameters were used as predictors. See the Appendix for additional information on how the permutation importance was calculated. The importance of each intervention parameter is shown in Figure 6.
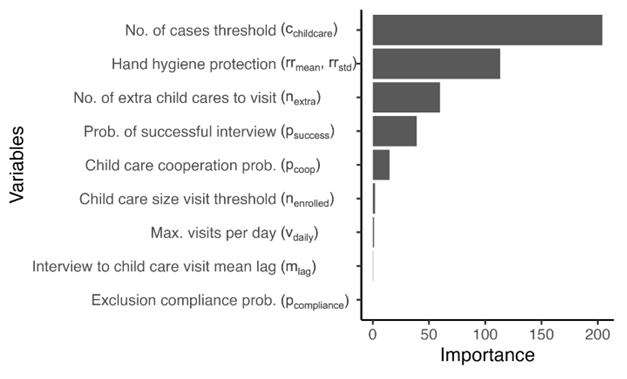
We found that the minimum number of reported cases that triggers a visit is the most important parameter, followed by the protective effect of hand hygiene education, the number of additional visits conducted, and the probability that an interview will be successful. Intervention characteristics like maximum visits per day (the visiting capacity) and the probability that a caregiver will comply and exclude the child from attending child care while infectious were found to have lower importance.
The mean efficacy of each of the parameters of the intervention is shown in Figure 7. For each plot, all other parameters are set to their optimal values. We see that reducing the number of cases that trigger a visit to a child care program from two to one increases the efficacy from 10% to 24%, while increasing the number of additional child care program visits from zero to four increases the efficacy by 10%. We can also see that an increase in successful interview probability from 47% to 70% increases the efficacy by 5%.
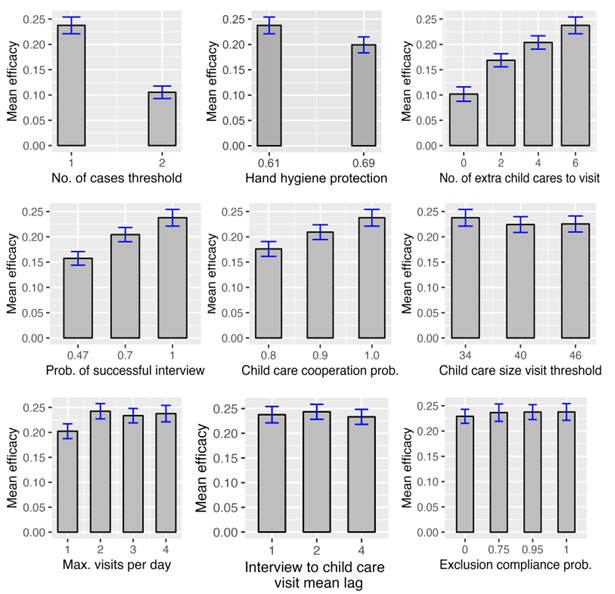
Parameters’ importance values may assist in choosing intervention scenarios that are feasible and effective by focusing on the central aspects of the interventions. For example, we can modify the previous scenario by incorporating the use of a non-antibacterial soap (\(rr_{mean} = 0.61\)) and increasing the extra number of scheduled visits to six (\(n_{extra} = 6\)). These modifications increase the efficacy from 6.5% to 11.8% (95% CI: 0.105, 0.131).
Discussion
We presented an agent-based model of Shigella transmission in Brooklyn’s Haredi communities. Agents represent children stratified by age and three types of mixing areas (households, child care programs or schools, and community sites) where transmission occurs. The model’s relative simplicity resulted in a low number of free parameters sufficient for the calibration of the model for the 2014-2015 outbreak that occurred in the communities. Including child care programs as places where transmission occurs allowed a straightforward representation of interventions that target child care programs. We presented scenarios of hand hygiene education dissemination during an outbreak by the public health authority by modeling steps the NYC Health Department has taken during previous outbreaks. The effects of different aspects of the interventions were evaluated by sampling the parameter space of interventions.
The model indicates that the efficacy of the interventions may be as high as 24% when all intervention parameters are at optimal values. However, as the optimal scenario may be unattainable in practice, we evaluated the importance of different parameters and found that some parameters influence the efficacy of the interventions more than others. The number of reported cases in a child care program that leads to a visit is highly important, as are the additional number of visits that are conducted in programs without known cases and incorporating the use of soap in hand hygiene education.
Interestingly, the maximum number of visits that can be conducted per day (the visit capacity) was found to be relatively unimportant. This finding is related to the low reporting proportion that reduces the number of cases observed and, in turn, reduces the number of visits to child care programs. In other words, the capacity is underutilized, and the outbreak can take off before sufficient visits are conducted. Being reactive and visiting child care programs only after infectious children are identified may be insufficient. As soon as it is determined that an outbreak may be underway, it might be beneficial to complement the visits triggered by reported cases and proactively use the capacity for additional visits to child care programs without reported cases. While the number of cases triggering a visit to a child care program was found to be the most important factor in controlling outbreaks, resource constraints during outbreaks might also preclude the health department from visiting programs when only single cases are identified. That is, lowering the visit threshold might be infeasible when many child care programs concurrently have reported cases.
The probability of child care programs to cooperate with the public health authority and the probability of a successful patient interview were also found to be important. This finding makes sense as these probabilities enable the dissemination of hand hygiene education, but the ability to increase these probabilities may be challenging in practice. Additional ways to creatively engage child care programs and schools to promote hand hygiene education during an outbreak will need to be considered, for example, by working with community partners to assist with hand hygiene education at facilities during an outbreak in place of a visit from public health authorities. Temporarily excluding infectious children from attending child care as required in the NYC Health Code was found to be less effective on its own than other considered interventions, possibly because of the short infectious period, and because by the time child care attendees were identified from patient interviews, they had already attended child care while infectious, allowing for Shigella introduction or continued transmission within programs.
The model is limited in several aspects. There is uncertainty regarding the values of some parameters and characteristics. For example, we assume a geometric distribution of the infectious and pre-infectious periods because of a lack of data. Different distributions may influence the model results (Krylova & Earn 2013). Uncertainty regarding the proportion of susceptible children at time 0 may also affect the results because data based on serum studies were unavailable.
We assumed that behavioral adaptations during the outbreak, such as increased household hygiene behavior, were limited and did not include them in the model. The only adaptation included is the removal of children from child care programs. The calibrated parameters may have absorbed the influence of such potential adaptations. Including such mechanisms is not difficult, but the associated parametrization may be challenging. The model includes basic demographic processes while keeping the size of the population constant. Agents aged 12 years old are removed and replaced by newborn susceptible agents, but the model assumes permanent immunity of recovered agents. These demographic assumptions may be reasonable when modeling one acute outbreak but may not be suitable for modeling multiple consecutive outbreaks over longer time scales. A list of additional limitations is offered in the Appendix.
The model can be modified for other aims, such as transmission among different communities, the study of Shigella vaccination programs once a vaccine is available, or the study of other pathogens that share similar transmission routes.
Acknowledgements
We thank community partners, as well as NYC Health Department staff who conduct interviews of reported shigellosis patients and health education specialists who conduct hand hygiene education in child care programs and schools. We thank Joshua M. Epstein for his contributions to the initial project discussions and for providing funds via NYU’s Agent-Based Modeling Laboratory. A preliminary version of this work was presented at the Annual Conference of the Council of State and Territorial Epidemiologists, West Palm Beach, Florida, June 12, 2018 (https://cste.confex.com/cste/2018/meetingapp.cgi/Paper/9509).Model Documentation
The model is available at: https://www.comses.net/codebase-release/ef59c50c-5ac0-4c8d-b673-8c3451e8d862/.Appendix
Reportable disease surveillance data
Cases of shigellosis are reportable by healthcare providers and laboratories to the NYC Health Department (New York City Health Code Article 11). The NYC Health Department Institutional Review Board reviewed the use of these data for this activity and deemed this work was public health surveillance that is non-research. We geocoded reported addresses of shigellosis patients \(< 12\) years old at specimen collection using the NYC Department of City Planning’s Geosupport System (Geographic Systems Section, Information Technology Division) to determine the census tract of residence (using 2010 boundaries) at the time of report.
Estimating the number of child care programs, schools, community sites, and agents
According to NYC Health Department Bureau of Child Care data, 263 City- and State-regulated child care programs existed in the area in 2017. However, we assumed that this is an underestimation as some programs are unregistered. Thus, we increased the number by 10% and created 289 child care programs. In 2017, 144 schools were estimated to be present in the area (Agudath Israel of America 2017) and 453 community sites, based on the number of synagogues (The Jewish Phonebook 2017). According to the NYC Health Department Bureau of Vital Statistics, the average number of births per year in the selected area was 6,600 between 2007 and 2015. The American Community Survey data indicate that 47.6% of the population that resided in the selected census tracts spoke either Yiddish or Hebrew at home (US Census Bureau). Therefore, we estimated the number of births per year that belong to the community as \(6,600 \times 0.476 = 3,141.6\). We assume that this number represents the number of children by year of age (i.e., \(3,141.6 \times 5 = 15,708\) \(<5\) year olds and \(3,141.6 \times 7 = 21,991\) \(5-<12\) year olds). This assumption allowed us to keep the population size constant while introducing new agents via births and removing agents who reach the age of 12 years. The model is quite flexible, and different assumptions about the target population can be incorporated as needed.
According to the Census of Jewish Day Schools in the United States, the number of children in Chasidic and Yeshiva world families was approximately 7.9 and 6.6 respectively (Schick 2000, Table 5). The census obtained these numbers by asking eighth-graders about the number of children in their families. We assumed that four of these 7.9 or 6.6 children are aged \(<12\) years old and set the average number of children \(<12\) years old in a household as four. In the model, we create one household for every four children and then assign agents randomly to households. However, this procedure results in a distribution of sizes in which a small fraction of households have a large number of children. We corrected this by assuming that the maximal number of children \(<12\) years old in a household is nine. Thus, instead of assigning an agent to a random household, we assign each agent to a random household that has fewer than nine children. This way, a household can have no more than nine agents. The small fraction of larger households (e.g., nine children in a household) may represent cohabitation of children of different families in one household unit.
Estimating the proportion of children with immunity at the start of an average outbreak
Monthly case counts were plotted and inspected visually to determine the outbreak and inter-outbreak (the time between the end of one outbreak and the start of the next) periods. Three outbreaks occurred during 2007–2017 (Figure 2). For each of the three outbreaks, we took the following steps:
- Generated a list of diagnosed cases, including birth dates
- Calculated the age of each infected child at the end of the outbreak
- Binned the ages into 24 age groups of 6-month intervals: \(\{[0,0.5), [0.5,1),\dots, [11.5,12)\}\)
- Produced a summary table of the total number of diagnosed cases by age group. Let \(T_{a,i}\) denote these counts of the number of diagnosed cases by age group \(a \in \{0, 0.5, \dots, 11.5\}\) at the end of the outbreak for outbreak \(I \in \{1, 2, 3\}\).
We converted the counts of diagnosed children (\(T_{a,i}\)) into the proportion of children of age group \(a\) who were infected (\(F_{a,i}\)) as follows:
| \[F_{a,i} = \frac{T_{a,i} \times k}{n \times r}\] | \[(4)\] |
- \(F_{a,i}\) is the proportion of children who were infected during outbreak \(i\) and were of age group \(a\) at the end of outbreak \(i\).
- \(T_{a,i}\) is the number of children who were diagnosed during outbreak \(i\) and were of age group \(a\) at the end of outbreak \(i\).
- \(k = 33.3\) is the estimated under-diagnosis multiplier for shigellosis in the U.S. (Scallan et al. 2011).
- \(n = 3,300\) is the half-year average number of births in the study area, 2007–2015 according to the NYC Health Department Bureau of Vital Statistics. The average number of yearly births is 6,600.
- \(r = 0.476\) is the proportion of persons speaking Yiddish or Hebrew at home, in the study area per the American Community Survey 2011-2015.
These proportions (\(F_{a,i}\)) were averaged across the three outbreak periods (\(F_a = \frac{F_{a,1} + F_{a,2} + F_{a,3}}{3}\)). \(F_a\) represents the average contribution of a single outbreak to the number of infected persons for the different age groups.
A visual inspection of case counts suggested that the period between the end of one outbreak and the end of the next outbreak was up to 3.5 years. Thus, a child belonging to age group \(a\) at the end of one outbreak used to belong to age group \(a - 3.5\) at the end of the previous outbreak (assuming that \(a \geq 3.5\)). Consequently, the number of outbreaks to which they were exposed depended on their age. We use \(F_a\) to estimate the cumulative effect of exposure to multiple outbreaks. We denote \(C_a\) as the average fraction of persons within age group \(a\) who were infected, taking into account all outbreaks having occurred during the group’s lifetime: \(C_a = F_{a} + F_{a-3.5} + \dots + F_{0}\)
By visual inspection, the inter-outbreak period (the time between the end of one outbreak and the start of the next) was approximately two years. As we would like the initial conditions to reflect the situation two years after an outbreak, we shifted \(C_a\) forward by two years (\(C'_a = C_a - 2\)), such that \([0,0.5)\) year-olds at the end of the prior outbreak were considered to be \([2, 2.5)\) year-olds after 2 years (at the start of the next outbreak), \([0.5, 1)\) year-olds would become \([2.5, 3)\) year-olds and so on, finishing with \([9.5, 10)\) year-olds who aged into \([11.5, 12)\) year-olds.
To estimate the fraction of children who are immune, we need to account for loss of immunity. At the start of the next outbreak, only 80% of \([2, 12)\) year-olds who had been infected and recovered at the end of the prior outbreak were assumed to retain their immunity (Cohen et al. 2014). Accordingly, we set the fraction of immune children as \(R_a = 0.8 \times C'_a\). As the model includes only two age groups, we averaged \(R_a\) within each age group: \(R_{[0,5)}\) and \(R_{[5,12)}\).
Estimation of the reproduction numbers
We estimated the net reproduction (\(R_{n}\)) and basic reproduction (\(R_{0}\)) numbers based on 100,000 simulations. For \(R_{n}\), we initiated the model using the estimated proportion of immune children, while for \(R_{0}\), all agents were initially susceptible with the exception of the first infectious agent. For each of the 100,000 realizations, we counted the number of agents that the infectious agent infected while not allowing any other agent to infect. The reproduction number estimation is the mean of the 100,000 counts. We find that \(R_{n} = 1.57\) (95% CI: 1.56, 1.59) and \(R_{0} = 1.62\) (95% CI: 1.61, 1.63). Thus, on average, the first infectious agent infects 1.57 agents given the initial proportion of susceptible that we use and 1.62 agents when all are susceptible.
The model and interventions parameters tables
| Parameter | Values | Source | NetLogo Variable |
|---|---|---|---|
| Mean infectious period | 7 days | Niyogi (2005), Joh et al. (2013), Shridhar et al. (2022) | mean-recovery-period |
| Mean pre-infectious period | 2 days | CDC (2020) | mean-incubation-period |
| Average number of children below the age of 12 in a household | 4 | See Appendix | household-mean-size |
| Number of child care programs | 289 | Agudath Israel of America (2017) and assumption | no-of-daycares |
| Number of schools | 144 | Agudath Israel of America (2017) | no-of-schools |
| Number of community sites | 453 | Agudath Israel of America (2017) | no-of-community-sites |
| Number of children by year of age | 3,141.6 | See Appendix | births-per-year |
| Parameter | Description | Values | Source | NetLogo Variable |
|---|---|---|---|---|
| \(p_{success}\) | The probability that an interview to ascertain child care attendance among reported cases is successful | 0.47*, 0.7**, 1.0** | *NYC Health Department data, **Assumption | prob-of-successful-interview |
| \(p_{compliance}\) | The probability that a caregiver will comply with a NYC Health Department order to temporarily exclude infectious child from attending child care | 0, 0.75, 0.95, \(1^{\dagger}\) | Assumption | exclusion-by-dohmh-prob |
| \(c_{childcare}\) | The minimum number of successfully interviewed cases in a child care program that triggers a hand hygiene education visit | 1, 2 | Assumption | no-of-case-threshold |
| \(p_{coop}\) | The cooperation probability of child care program to participate in a hand hygiene education visit | 0.8*, 0.9**, 1.0** | *NYC Health Department staff expert opinion, **Assumption | daycare-cooperation-prob |
| \(m_{lag}\) | The mean of the exponentially distributed lag of weekdays between successful interview of reported case attending child care program and scheduled visit to that program | 1, 2, 4 | Assumption | Interview-to-daycare-visit-mean-lag |
| \(v_{daily}\) | The maximum number of child care program visits per weekday that can be performed (the visit capacity) | 1, 2, 3, 4 | Assumption | max-visits-per-day |
| \((rr_{mean}, rr_{std})\) | The relative risk (\(rr_{mean}\)) of illness after hand hygiene education intervention, without and with use of non-antibacterial soap; the standard error (\(rr_{std}\)) of the relative risk estimate | Two estimations: Without soap (0.61, 0.178), With soap (0.69, 0.163) | Aiello et al. (2008) | ln-mean-hand-washing-rr, ln-std-hand-washing-rr |
| \(n_{enrolled}\) | The minimal number of enrolled children that makes an extra child care program eligible for a visit | \(34, 40, 46 ^{\mp}\) | Assumption | daycare-size-visit-threshold |
| \(n_{extra}\) | The number of extra child care programs to visit, if visits capacity allows | \(0, 2, 4, 6 ^{\diamond}\) | Assumption | no-of-nearby-daycare-to-visit |
Testing for a change in the proportion of large outbreaks
We tested the hypothesis that the proportion of major outbreaks is unaffected by the interventions. We tested this hypothesis by comparing the proportion of major outbreaks in each intervention (parameter set) with the no intervention scenario. For each of the 17,280 parameter sets, we constructed a 2 by 2 contingency table, counting the number of major outbreaks and the number of no outbreaks for the 1,000 simulations when the intervention is on and when the intervention is not used (the base scenario). We found that none of the parameter sets had a significant difference in the proportion of outbreaks with and without intervention. Chi-square tests and the Benjamini-Hochberg procedure were used to control the false discovery rate at 0.05. In the rest of the analysis, we only consider major outbreaks.
Estimating the importance of intervention parameters
To estimate the importance of each of the intervention parameters, we used the ranger package (Wright & Ziegler 2017) of R to fit a random-forest regression. The total number of infections was used as the outcome variable, while the intervention parameters were used as predictors. We used 70% of the runs for training and the rest for validation. A variable importance is estimated by calculating each tree’s out-of-bag prediction error (mean squared error). The values of each variable are permuted, and prediction accuracy is recalculated. For each tree, the permutation importance for the variable of interest is the difference between the original and permuted prediction accuracies. The average importance value of all trees in the random forest is the permutation importance of the variable (Wright et al. 2016).
Limitations
- We assume transmission is driven entirely by children, ignoring any effect of adult caregivers and food handlers.
- We assume no immigration into or emigration out of the study area, implying that all children were born and live their entire lives in the study area.
- We assume the population size and set of transmission sites are static over time.
- We assume transmission is sustained entirely within the community’s households, child care programs, schools, and community sites, with no travel or introductions of infection from outside the community after the simulation begins and no other important mixing sites.
- We assume children attend the same child care program and school year-round, ignoring different child care arrangements in the summer.
- We assume that transmission dynamics do not vary according to whether children are girls or boys, although children in this community are segregated by sex in child care programs and schools.
- We assume that once infection is introduced into any given household, child care program, school, or community site, all children at that location are potentially exposed with homogeneous mixing (e.g., no stratification by age in years, by diaper vs. toilet-trained status, nor by classroom).
- In counting infections, we do not distinguish according to whether they are symptomatic, tested, or ascertained by the health department. In fact, these distinctions affect transmission because symptomatic children are more likely to transmit because of hand hygiene issues with loose stools, some symptomatic children might be kept at home by parents while having diarrhea, and the health department can only exclude cases it ascertains.
- Based on two observed inter-outbreak periods between three outbreaks, we assume the inter-outbreak period is exactly two years. A longer inter-outbreak period would modify the model’s initial conditions by decreasing the proportion recovered and immune at the start of the modeled outbreak.
- We assume only one Shigella sonnei strain circulates within this community.
- In calibrating to empirical data, we assume no interventions during historical outbreaks.
- The size of the target population and the percentages of immune children were not measured directly. Inaccuracies may influence the efficacy estimations.
- We assume the under-diagnosis multiplier (\(k\)) does not change over time. In fact, a higher proportion of cases could be undiagnosed during the second half of the outbreak because once one symptomatic person in a household seeks health care and is tested and diagnosed, there may be limited utility of additional care seeking by that household.
- The efficacy estimations of the hand hygiene interventions are highly dependent on the estimations of hand hygiene education effect parameters (\(rr_{mean}\), \(rr_{std}\)).
References
AGUDATH Israel of America. (2017). Personal communication. Deborah Zachai, Director of Education Affairs.
AIELLO, A. E., Coulborn, R. M., Perez, V., & Larson, E. L. (2008). Effect of hand hygiene on infectious disease risk in the community setting: A meta-analysis. American Journal of Public Health, 98(8), 1372–1381. [doi:10.2105/ajph.2007.124610]
ALFASI, N., Flint Ashery, S., & Benenson, I. (2013). Between the individual and the community: Residential patterns of the Haredi population in Jerusalem. International Journal of Urban and Regional Research, 37(6), 2152–2176. [doi:10.1111/j.1468-2427.2012.01187.x]
ALTMAN, D. G. (1991). Practical statistics for medical research. New York, NY: Chapman & Hall.
ALUKO, S. K., Ishrati, S. S., Walker, D. C., Mattioli, M. C., Kahler, A. M., Esschert, K. L. V., Hervey, K., Rokisky Jr, J., Wikswo, M. E., Laco, J. P., Kurlekar, S., Byrne, A., Molinari, N. A., Gleason, M. E., Steward, S., Hlavsa, M. C., & Neises, D. (2022). Outbreaks of acute gastrointestinal illness associated with a splash pad in a wildlife park – Kansas, June 2021. Morbidity and Mortality Weekly Report, 71(31), 981. [doi:10.15585/mmwr.mm7131a1]
BOWEN, A., Eikmeier, D., Talley, P., Siston, A., Smith, S., Hurd, J., Smith, K., Leano, F., Bicknese, A., Norton, J. C., & Campbell, D. (2015). Outbreaks of Shigella sonnei infection with decreased susceptibility to azithromycin among men who have sex with men - Chicago and metropolitan Minneapolis-St. Paul, 2014. Morbidity and Mortality Weekly Report, 64(21), 597. https://www.cdc.gov/mmwr/preview/mmwrhtml/mm6421a7.htm
BRITTON, T. (2010). Stochastic epidemic models: A survey. Mathematical Biosciences, 225(1), 24–35. [doi:10.1016/j.mbs.2010.01.006]
CARIAS, C., Undurraga, E. A., Hurd, J., Kahn, E. B., Meltzer, M. I., & Bowen, A. (2019). Evaluation of the impact of shigellosis exclusion policies in childcare settings upon detection of a shigellosis outbreak. BMC Infectious Diseases, 19(1), 1–7. [doi:10.1186/s12879-019-3796-7]
CDC. (2001). Shigella sonnei outbreak among men who have sex with men - San Francisco, California, 2000-2001. Morbidity and Mortality Weekly Report, 50(42), 922-926. Available at: https://www.cdc.gov/mmwr/preview/mmwrhtml/mm5042a3.htm
CDC. (2020). Questions & answers Shigella. Retrieved April 11, 2022, from: https://www.cdc.gov/shigella/general-information.html
CDC. (2023). National outbreak reporting system dashboard. Accessed July 25, 2023. Available from: https://wwwn.cdc.gov/norsdashboard/.
CHATURVEDI, O., Masupe, T., & Masupe, S. (2014). A continuous mathematical model for Shigella outbreaks. American Journal of Biomedical Engineering, 4(1), 10–16. [doi:10.5923/j.ajbe.20140401.02]
CHEN, T., Leung, R. K. K., Zhou, Z., Liu, R., Zhang, X., & Zhang, L. (2014). Investigation of key interventions for shigellosis outbreak control in China. PLoS One, 9(4), e95006. [doi:10.1371/journal.pone.0095006]
COHEN, D., Bassal, R., Goren, S., Rouach, T., Taran, D., Schemberg, B., Peled, N., Keness, Y., Ken-Dror, S., Vasilev, V., Nissan, I., Agmon, V., & Shohat, T. (2014). Recent trends in the epidemiology of shigellosis in Israel. Epidemiology & Infection, 142(12), 2583–2594. [doi:10.1017/s0950268814000260]
COHEN, D., Korin, H., Bassal, R., Markovich, M. P., Sivan, Y., Goren, S., & Muhsen, K. (2019). Burden and risk factors of Shigella sonnei shigellosis among children aged 0-59 months in hyperendemic communities in Israel. International Journal of Infectious Diseases, 82, 117–123. [doi:10.1016/j.ijid.2019.02.031]
DE SCHRIJVER, K., Bertrand, S., Garitano, I. G., Van DEn Branden, D., & Van Schaeren, J. (2011). Outbreak of Shigella sonnei infections in the Orthodox Jewish community of Antwerp, Belgium, April to August 2008. Eurosurveillance, 16(14), 19838. [doi:10.2807/ese.16.14.19838-en]
EDWARD, S., Mureithi, E., & Shaban, N. (2020a). Shigellosis dynamics: Modelling the effects of treatment, sanitation, and education in the presence of carriers. International Journal of Mathematics and Mathematical Sciences, 2020, 3476458. [doi:10.1155/2020/3476458]
EDWARD, S., Shaban, N., & Mureithi, E. (2020b). Optimal control of shigellosis with cost-effective strategies. Computational and Mathematical Methods in Medicine, 2020, 9732687. [doi:10.1155/2020/9732687]
GARRETT, V., Bornschlegel, K., Lange, D., Reddy, V., Kornstein, L., Kornblum, J., Agasan, A., Hoekstra, M., Layton, M., & Sobel, J. (2006). A recurring outbreak of Shigella sonnei among traditionally observant Jewish children in New York City: The risks of daycare and household transmission. Epidemiology & Infection, 134(6), 1231–1236. [doi:10.1017/s0950268806006182]
GLUSHCHENKO, O. E., Prianichnikov, N. A., Olekhnovich, E. I., Manolov, A. I., Tyakht, A. V., Starikova, E. V., Odintsova, V., Kostryukova, E. S., & Ilina, E. I. (2019). VERA: Agent-based modeling transmission of antibiotic resistance between human pathogens and gut microbiota. Bioinformatics, 35(19), 3803–3811. [doi:10.1093/bioinformatics/btz154]
HERRERA, C. M., Schmitt, J. S., Chowdhry, E. I., & Riddle, M. S. (2022). From Kiyoshi Shiga to present-day Shigella vaccines: A historical narrative review. Vaccines, 10(5), 645. [doi:10.3390/vaccines10050645]
HEYMANN, D. L. (2008). Control of communicable diseases manual. American Public Health Association
HINES, J. Z., Pinsent, T., Rees, K., Vines, J., Bowen, A., Hurd, J., Leman, R., & Hedberg, K. (2016). Notes from the field: Shigellosis outbreak among men who have sex with men and homeless persons - Oregon, 2015–2016. Morbidity and Mortality Weekly Report, 65, 812–813. [doi:10.15585/mmwr.mm6531a5]
JOH, R. I., Hoekstra, R. M., Barzilay, E. J., Bowen, A., Mintz, E. D., Weiss, H., & Weitz, J. S. (2013). Dynamics of shigellosis epidemics: Estimating individual-level transmission and reporting rates from national epidemiologic data sets. American Journal of Epidemiology, 178(8), 1319–1326. [doi:10.1093/aje/kwt122]
KRYLOVA, O., & Earn, D. J. (2013). Effects of the infectious period distribution on predicted transitions in childhood disease dynamics. Journal of the Royal Society Interface, 10(84), 20130098. [doi:10.1098/rsif.2013.0098]
LAMPEL, K. A., & Sandlin, R. (2003). Shigella. In B. Caballero, L. C. Trugo, & P. M. Finglas (Eds.), Encyclopedia of Food Sciences and Nutrition. Amsterdam: Elsevier. [doi:10.1016/b0-12-227055-x/09004-0]
MATTISON, C. P., Calderwood, L. E., Marsh, Z. A., Wikswo, M. E., Balachandran, N., Kambhampati, A. K., Gleason, M. E., Lawinger, H., & Mirza, S. A. (2022). Childcare and school acute gastroenteritis outbreaks: 2009-2020. Pediatrics, 150(5), e2021056002. [doi:10.1542/peds.2021-056002]
NEW YORK CITY HEALTH CODE ARTICLE 11. Reportable diseases and conditions. Available at: https://www1.nyc.gov/assets/doh/downloads/pdf/about/healthcode/health-code-article11.pdf.
NIYOGI, S. K. (2005). Shigellosis. Journal of Microbiology, 43(2), 133–143.
PARTHASARATHY, A. (2013). Textbook of pediatric infectious diseases. London: JP Medical Ltd.
PIRUTINSKY, S., Cherniak, A. D., & Rosmarin, D. H. (2020). COVID-19, mental health, and religious coping among American Orthodox Jews. Journal of Religion and Health, 59, 2288–2301. [doi:10.1007/s10943-020-01070-z]
REW, V., Mook, P., Trienekens, S., Baker, K. S., Dallman, T. J., Jenkins, C., Crook, P. D., & Thomson, N. R. (2018). Whole-genome sequencing revealed concurrent outbreaks of shigellosis in the English Orthodox Jewish Community caused by multiple importations of Shigella sonnei from Israel. Microbial Genomics, 4(3), e000170. [doi:10.1099/mgen.0.000170]
SCALLAN, E., Hoekstra, R. M., Angulo, F. J., Tauxe, R. V., Widdowson, M. A., Roy, S. L., Jones, L. J., & Griffin, P. M. (2011b). Foodborne illness acquired in the United States - Major pathogens. Emerging Infectious Diseases, 17(1), 7. [doi:10.3201/eid1701.09-1101p1]
SCHICK, M. (2000). A census of Jewish day schools in the United States. Avi Chai Foundation, New York
SHRIDHAR, S. V., Alexander, M., & Christakis, N. A. (2022). Characterizing super-spreaders using population-level weighted social networks in rural communities. Philosophical Transactions of the Royal Society A, 380(2214), 20210123. [doi:10.1098/rsta.2021.0123]
SOBEL, J., Cameron, D. N., Ismail, J., Strockbine, N., Williams, M., Diaz, P. S., Westley, B., Rittmann, M., DiCristina, J., Ragazzoni, H., Tauxe, R. V., & Mintz, E. D. (1998). A prolonged outbreak of Shigella sonnei infections in traditionally observant Jewish communities in North America caused by a molecularly distinct bacterial subtype. The Journal of Infectious Diseases, 177(5), 1405–1409. [doi:10.1086/517825]
The Jewish Phonebook. (2017). Brooklyn, NY. 2017. App version available at: https://play.google.com/store/apps/details?id=com.info718&hl=en_US&gl=US.
TONI, T., Welch, D., Strelkowa, N., Ipsen, A., & Stumpf, M. P. (2009). Approximate Bayesian computation scheme for parameter inference and model selection in dynamical systems. Journal of the Royal Society Interface, 6(31), 187–202. [doi:10.1098/rsif.2008.0172]
U.S. Census Bureau. B16001: Language spoken at home by ability to speak English for the population 5 years and over.
VYNNYCKY, E., & White, R. (2010). An introduction to infectious disease modelling. Oxford: Oxford University Press.
WIKSWO, M. E., Kambhampati, A., Shioda, K., Walsh, K. A., Bowen, A., & Hall, A. J. (2015). Outbreaks of acute gastroenteritis transmitted by person-to-person contact, environmental contamination, and unknown modes of transmission - United States, 2009-2013. Morbidity and Mortality Weekly Report: Surveillance Summaries, 64(12), 1–16. [doi:10.15585/mmwr.ss6412a1]
WILENSKY, U. (1999). NetLogo. Center for Connected Learning and Computer-Based Modeling, Northwestern University, Evanston, IL. Available at: http://ccl.northwestern.edu/netlogo/.
WRIGHT, M. N., & Ziegler, A. (2017). ranger: A fast implementation of random forests for high dimensional data in C++ and R. Journal of Statistical Software, 77(1), 1–17. [doi:10.18637/jss.v077.i01]
WRIGHT, M. N., Ziegler, A., & König, I. R. (2016). Do little interactions get lost in dark random forests? BMC Bioinformatics, 17(1), 1–10. [doi:10.1186/s12859-016-0995-8]
ZHAO, Z., Yang, M., Lv, J., Hu, Q., Chen, Q., Lei, Z., Wang, M., Zhang, H., Zhai, X., ZHAO, B., Su, Y., Chen, Y., Zhang, X. S., Cui, J. A., Frutos, R., & Chen, T. (2022). Shigellosis seasonality and transmission characteristics in different areas of China: A modelling study. Infectious Disease Modelling, 7(2), 161–178. [doi:10.1016/j.idm.2022.05.003]