Mechanisms Behind Public School Enrollment Trends in School Choice Systems: The Case of Chile

, , ,
and
aUniversidad de O'Higgins, Chile; bArizona State University, United States of America; cUniversidad de Chile, Chile; dUniversidad Adolfo Ibáñez, Chile
Journal of Artificial
Societies and Social Simulation 27 (4) 2
<https://www.jasss.org/27/4/2.html>
DOI: 10.18564/jasss.5436
Received: 20-Nov-2023 Accepted: 04-Jul-2024 Published: 31-Oct-2024
Abstract
Market-based reforms in education have expanded worldwide, often raising questions about their impact on the strength and sustainability of the public education sector. In this paper, we explore how such “school choice” policies affected public school enrollment in Chile, a country where a nationwide school choice reform coincided with a decline in public enrollment. To better understand the factors driving the public enrollment decline, we develop an agent-based model representing the education system in Chile between 2004 and 2016. We calibrate our model to data from four cities and conduct simulation experiments that disentangle the impacts of the hypothesized explanations for the decline. Our analysis reveals the importance of an institutional factor largely outside the core of the school choice policy – the grade-span configuration of schools in each sector. It also suggests that creating a formal coordination mechanism among primary and secondary public schools, to ensure students graduating from a primary public school a seat at a secondary public school, may be a promising policy for strengthening public enrollment. Other implications for understanding the decline in Chilean public enrollment are also discussed.Introduction
Over the last decades, educational policies that provide households increased choice in schools have expanded worldwide and private education has grown in middle- and low-income countries (Elacqua et al. 2018; Verger et al. 2018). Advocates of such “school choice” policies argue that they benefit students by enriching the range of available options and by promoting competition among schools (Canals et al. 2019; Loeb & Valant 2020). While the aggressiveness with which school choice policies have been carried out varies across countries, even the most extreme market-oriented policies imply the continuity of the public sector (Ladd & Fiske 2020; Musset 2012; OECD 2020). As maintaining a healthy and sustainable public sector education system remains an important goal in most countries, a relevant question that arises with the growth of school choice policies relates to their impact on public school enrollment.
One country where school choice policies are thought to have a great impact on public school enrollment is Chile. Chile, a country where people can choose among public, private voucher, and private fee-paying schools, is an extreme example of a market-oriented school choice system (Ladd & Fiske 2020). Since the 80s, when market-based reforms were implemented, there has been a significant decline in public sector enrollment. Several explanations have been proposed for this decline, including hypotheses related to the larger availability of private voucher schools, a decrease in public school quality, among others (Bellei et al. 2010; Paredes & Pinto 2009; Raczynski et al. 2010; Zapata 2010). In practice, elements of several of those explanations likely operated simultaneously, making it difficult to isolate which policy and contextual features contributed most to the decline. Furthermore, enrollment is dynamic and depends on interdependent decisions. Families’ school choices – which depend on their geographic and social positions – can affect the decisions of others in their social network, leading to feedback processes that may reinforce the observed trends. Extrapolating outcomes from one context to another in such cases is extremely challenging (Maroulis et al. 2010).
To address such complexity, we developed an agent-based model (ABM) depicting Chile’s education system. This approach allows us to represent important aspects of the school choice process that are usually not explicitly modeled. It enables the representation of heterogeneous agents interacting, the existence of a social network through which they can influence each other, and geographic considerations related to selecting a school (Macal & North 2010). Importantly, it also allows us to focus on the changes in school enrollment over time.
Using an ABM to model school enrollment trends also offers at least two other advantages. First, it helps to address a methodological challenge: Many of the processes affecting public school enrollment in Chile are related to national policies that were simultaneously implemented in the whole country and, often, temporarily overlapped with each other. Consequently, empirical data lack the variance needed to isolate the effect of one policy or mechanism. In contrast, ABMs enable us to examine the impact of any single factor by simulating counterfactual scenarios where we modify one element at a time (Canessa et al. 2023).
Second, computational modeling aids in the theory-building process. Each model component must be precisely defined for translation into code, compelling us to sharpen and refine our hypotheses. Furthermore, the analysis of the model provides intuition about the consequences of different mechanisms. The theory strengthening and insights gained through this approach can guide future empirical analysis (Maroulis 2016).
Once we developed an ABM grounded in the Chilean school system, we calibrated it for four different cities using student, school, and geographic data from 2004-2016, and conducted simulation experiments that carefully isolated the role of policy design features and context factors on public school enrollment trends. Our simulation experiments revealed the potential importance of an institutional factor in determining public school enrollment decline often overlooked – the grade-span configuration of schools in each sector. Our analysis also suggests that creating a formal coordination mechanism among primary and secondary public schools, to ensure students graduating from primary public schools a seat at a secondary public school, may be a particularly promising policy for strengthening public sector enrollment.
Agent-Based Models for Education Enrollment
Education systems have several characteristics of complex systems – they are interconnected, path-dependent, affected by feedback loops, and have emergent properties (Ghaffarzadegan et al. 2017; Jacobson et al. 2019) – making them excellent candidates for investigation through agent-based modeling. Previous ABM work in education has studied higher education choices (Leoni 2022; Reardon et al. 2016, 2018), primary and secondary education enrollment (Díaz et al. 2019; Harland & Heppenstall 2012; Maroulis et al. 2014; Maroulis 2016; Millington et al. 2014; Stoica & Flache 2014), and sequential educational decisions (Manzo 2013). The most common aim of these studies is to understand the mechanisms behind a real-world pattern or to study the consequences of a current or potential public policy.
Research that studies the mechanisms behind real-world patterns often runs computational experiments with different mechanisms activated, looking to ascertain their contribution to a given outcome. For instance, Reardon et al. (2016) study the mechanisms leading to socioeconomic stratification between U.S. colleges, while Manzo (2013) explores the ones driving stratification between educational levels in France. For the case of the primary and secondary school system, Millington et al. (2014) investigate the mechanisms behind London’s empirical patterns about the relationship between students’ school performance, schools’ popularity, and students’ travel distance from home to school, and Harland & Heppenstall (2012) examine, for the case of England, different admission and school choice rules and their effect on students being correctly allocated to their schools.
Studies on public policy effects often simulate policy "treatments" or scenarios. For example, Leoni (2022) analyzes strategies aimed at increasing higher education enrollment in the Italian context, and Reardon et al. (2018) investigate socioeconomic affirmative action’s effect on the diversity of college enrollment in the US. This approach has been used in primary and secondary education to study the transition from a neighborhood-based to a school choice-based education system in the U.S. (Maroulis et al. 2014; Maroulis 2016). Of particular note is a study by Díaz et al. (2019), who adapted the model developed by Maroulis et al. (2014) to the Chilean context, and calibrated it for the capital city, Santiago. Díaz et al. (2019) used the model to analyze the implications of information asymmetries in traffic lights, a Chilean policy enacted to provide households with schools’ performance information.
In this paper, we contribute to this understanding of the public school enrollment decline in Chile by developing an empirically grounded model that incorporates several additional salient factors in the Chilean system, such as capacity constraints and student selection procedures, social network effects, demographics changes, and public policy interventions. Acknowledging that educational markets are geographic and that there is variation within the country, we calibrate our model separately for four different-sized Chilean cities. In this sense, our study relates to the two approaches described. It belongs to the first group as it aims to understand an empirical pattern -the public enrollment decline in Chile. It aligns with the second group of studies, as we conduct counterfactual experiments representing public policies that could have been applied.
The Chilean Educational Context
School sectors in the Chilean school system
In the 1980s, a set of market-oriented policies were put in place in Chile. A voucher-type student-based subsidy was introduced with the aim of encouraging schools to compete for students and spurring improvement in the quality and efficiency of the education system (Ladd & Fiske 2020). In addition, the administration of public schools was decentralized. These changes resulted in three main types of schools: public schools operated by municipalities and receiving public vouchers; private voucher schools, operated by private entities and also receiving public vouchers; and private fee-paying schools, both operated and funded by private tuition payments (Mizala & Torche 2012). A relevant feature of the Chilean school choice system is that students can apply to any school -regardless of their residential location. Also, until 2016, school applications were evaluated independently by each school1.
During the 1990s and 2000s, the core of the system remained unchanged but was subject to some modifications (Canals et al. 2019). Three changes were the most important. First, starting in 1993, private voucher schools were allowed to charge higher tuition2(Mizala & Torche 2012). Second, in 1997, the Jornada Escolar Completa law (JEC) (MINEDUC 1997), which intended to extend the school day, was approved and implemented nationwide. The reform included competitive public funds for public and private voucher schools to expand their infrastructure and build new schools in deprived areas. A regulation approved in 2004 allowed these funds also to be used for primary and secondary schools from those areas, aiming at extending their supply to both educational levels (MINEDUC 2004). Third, in 2008 the Preferential School Subsidy reform (SEP) transformed the flat voucher system into a means-tested one. With that reform, public and private voucher schools joining the SEP program received an extra per-student subsidy when enrolling economically disadvantaged students, conditional on offering those students tuition-free education. Schools’ enrollment into the means-tested voucher program is voluntary. These schools could also receive an additional subsidy for enrolling a high proportion of disadvantaged students (Mizala & Torche 2012).
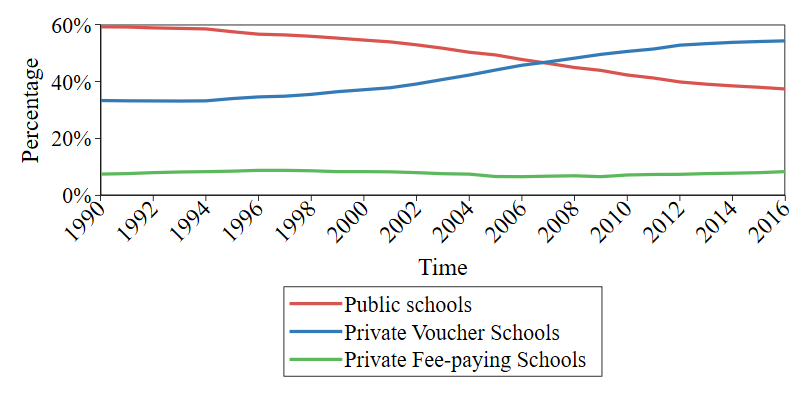
By 2016, 37% of Chilean students were studying at a public school, 54% at a private voucher school, and 8% at a private fee-paying school. Private fee-paying schools were characterized by higher tuition fees, students from higher socioeconomic status (SES), and higher average achievement on the System of Measurement of Education’s Quality (SIMCE, in its Spanish acronym), a national standardized achievement test. Private voucher schools had lower tuition and SIMCE scores and enrolled students from lower SES compared to fee-paying private schools. Public schools were mostly free of charge, enrolled students from lower SES, and had lower SIMCE scores than both private sector schools. As a result, in Chile, public schools are usually perceived as lower quality options when compared to private ones (Raczynski et al. 2010). However, once the differences in SES are controlled for, the disparities in SIMCE scores between public and private voucher schools become small or insignificant (Lara et al. 2011). School sectors also had different grade-span configurations. In 2016, 83% of public schools offered only primary education (grades 1-8), 10% only secondary education (grades 9-12) or primarily secondary education (grades 7-12), and 7% offered both education levels (grades 1-12). This contrasts with the other sectors. 51% of private voucher schools offered only primary education, while 39% offered both educational levels - an increase from 26% in 2004. Meanwhile, 85% of private fee-paying schools offered both educational levels3.
Following Chile’s market-oriented school reforms, public school enrollment declined while private voucher school enrollment increased (See Figure 1). Motivated by perceived inequities in the voucher system and public system abandonment, student protests led to structural reforms approved since 2015 to reduce the influence of the market (Bellei & Munoz 2023; Cummings et al. 2023). Those reforms included changes such as private voucher schools progressively becoming tuition-free, introducing a centralized application system to prevent the "cream skimming" of students, and the transfer of public schools’ administration from municipalities to new public entities that operate the schools of adjacent municipalities (MINEDUC 2019a, 2019b). Our analysis covers the period before the implementation of these reforms when the market role was preponderant.
Explanations for public school enrollment decline in Chile
In this section, we outline hypotheses related to the decline of public school enrollment in Chile. The first four hypotheses draw on the previous discussion about the Chilean case. The two last ones are additional explanations not emphasized in the literature. Each hypothesized explanation highlights a different element that may affect public enrollment and should be included in the model.
H1: Public enrollment decreased because the supply of private voucher schools increased vis a vis the supply of public schools. Scholars studying the decline in public school enrollment in Chile have pointed out that this decline is related to the incentives created by the nationwide voucher policy. Specifically, it has been argued that this policy produced an increase in the number of private voucher schools that, coupled with a limited capacity to open new public schools, led to a decline in public school enrollment (Bellei et al. 2010; Paredes & Pinto 2009). This explanation implies that the entry of new schools is a factor that should be included in the model (Element 1).
H2: Public enrollment decreased because public schools reduced their appeal. Evidence about family preferences in Chile associates public schools with lower quality and lower discipline, when compared to private ones, and with an increasing number of teacher strikes (Raczynski et al. 2010; Zapata 2010). Moreover, it has been shown that decreases in families’ satisfaction with school quality are associated with increases in the percentage of families switching schools (Canals 2016). Thus, a decrease in the appeal of public schools may have produced the reduction in public enrollment. This hypothesis implies that the academic performance of public schools is an important element to include in the model (Element 2).
H3: Public enrollment decreased because the population attending primary education has decreased.To the extent that sectors differ in the proportion of their supply that serves primary school grades, it has been proposed that changes in the number of school-aged children over time can impact enrollment trends. In Chile, population changes could have affected the enrollment trends, given that the number of primary school students may have dropped due to a decline in the birth rate observed during the last decades (World Bank 2022). As a result, public school enrollment could have suffered the most, as this sector offers primary education more frequently than the others (Canals et al. 2015; Paredes & Pinto 2009). This is especially true in rural areas, where primary education provision is mostly public (Núñez et al. 2015). This implies that the new primary student entry is potentially an important determinant of public sector enrollment (Element 3).
H4: Public enrollment decrease was reinforced by the SEP program. Considering that many private voucher schools have charged tuition since the 1993’s reform, low-income students had more limited school options. In this context, the SEP program introduced in 2008 allowed economically disadvantaged students to study for free in private voucher and public schools ascribed to the program. Despite the concern that the program might lead to a decline in public enrollment by encouraging students to switch to the private voucher sector, previous studies have failed to find large effects (Centro de Estudios MINEDUC 2015; Flores 2020; Navarro-Palau 2017). Still, the existence of the means-tested vouchers should be considered when examining changes to public enrollment in Chile (Element 4).
H5: Public enrollment decreased because in the public sector most students must switch schools to attend secondary education. Considering differences in the grade-span configuration of schools in each sector – likely related to the 2004 incentive to expand the educational levels offered by the schools and a limited public capacity for expansion (Bellei et al. 2010; MINEDUC 2004) –, we propose two reasons this may impact public school enrollment. First, as fewer public schools offer both educational levels, students from those schools are more frequently compelled to switch schools, having more chances to move to another school sector. Second, in the case of India, it has been stated that differences in grade-span configuration can impact cross-sector enrollment trends when parents prefer schools offering all grade levels (Juneja 2007; Mousumi & Kusakabe 2019). For contexts where most secondary education is private, Juneja (2007) proposed the “blocked chimney effect”: parents prefer schools with both primary and secondary education to reduce the risk of not finding a good school option when seeking secondary education, which results in a decline in public enrollment. Thus, Chilean parents may also prefer schools offering both educational levels - to avoid being forced to search again-, which could also harm the public sector. Consequently, grade-span configuration of schools in each sector is an important element to include in a model that examines changes in public enrollment (Element 5).
H6: Public enrollment decreased because the population’s SES increased. Wide international evidence has shown that high-SES families are more likely to choose private schools (Dixon et al. 2017; Farre et al. 2018; Lara et al. 2011; Parma 2022). As a consequence, changes over time in the socioeconomic composition of the population can impact public school enrollment trends. Considering that Chile’s GDP per capita and population’s average schooling years have increased over time (Mieres Brevis 2020), the population’s SES trend may have increased the number of families that can afford private voucher schools. Consequently, this could have produced a decrease in public school enrollment. Therefore, the SES trends of the population should also be included in the model (Element 6).
Methods
In this section, we describe the agent-based model used in the paper. We first present an overview of the model. This is followed by a description of Chilean school system data used in this study. We then explain how those data were used to calibrate the parameters in the model and conclude by presenting how we validated the output of the model. Additional details are provided in the Appendices (Model Description, Appendix A; Model Initialization, Appendix B; Model Calibration; Appendix C, Model Validation, Appendix D).
Model
The model consists of students and schools located on a grid that represents the geography of the particular city used for calibration (Figure 2). Each time period of the model represents one year. Each year, the students and schools make decisions and experience changes based on the rules and conditions articulated below. The model simulates the dynamics driving school enrollment for 12 years4,5.
Each school \(j\) has the following attributes:
- Geographic location.
- School sector (Public / Private Voucher / Private Fee-paying).
- Value-added (VA), which represents the school’s yearly contribution to students’ achievement.
- Selectivity (selective/non-selective school).
- Maximum capacity by grade level.
- Year of opening.
- Year of closing.
- Year of subscription to the SEP program.
- Probability of being known through public information (\(p_j\)).
- Grade-span configuration (1°- 4° grade levels / 1°- 6° grade levels / 1° – 8 ° grade levels / 5° - 12° grade levels / 7° - 12° grade levels / 9° - 12° grade levels / 1° - 12° grade levels)6.
- Mean achievement of enrolled students.
- Monthly tuition.
The model represents real schools and their experiences over the years of 2004-2016. Attributes 1-10 are therefore exogenously assigned to schools using a dataset that contains information for each school for each of those years, which we will refer to as the “school input data.” Attributes 11-12 are determined endogenously during the simulation.
In addition, the model represents a population of simulated students. Students have the following characteristics:
- Geographic location.
- Parents’ educational level (EL), measured on average schooling years.
- Academic achievement.
- Economically disadvantaged student, which indicates whether the student is considered eligible for free-tuition in schools participating in the SEP program.
- Budget restriction, defined by the maximum tuition that the student can afford.
- Preference class, a variable that groups students based on the schools’ variables that they value when choosing a school.
- Grade level.
- Current school.
- Choice-set, the set of schools that the student considers as an option when choosing school.
- Social Network, other students from whom a student can gain information about schools, and that can influence the student’s school choice.
Once a student appears in the model, attributes 1-6 are assigned, using synthetic data that is representative of their census block, or statistical models that were estimated outside of the simulation. Those attributes remain fixed over time. Attributes 7-10 are endogenously determined during the simulation and may vary throughout the student’s school life.
We initialize the model to replicate the 2004 Chilean school system. To do so, initial school attributes are based on city-specific data, and an initial set of students is simulated to mirror the 2004 school population of that city. Then, to simulate an initial state that is the result of the model itself, the model iterates until reaching a steady state. Refer to Appendix B for a detailed description of these initialization processes. Note that our analysis focuses on the enrollment trends between said steady state and the simulation of the year 2016. Therefore, as it is commonly done, the initial transient phase – embedded in our setup process – is neglected (Bargigli et al. 2016).
Figure 3 presents an overview of one iteration of the model, which represents a school year. In one iteration, the following four main phases sequentially occur.
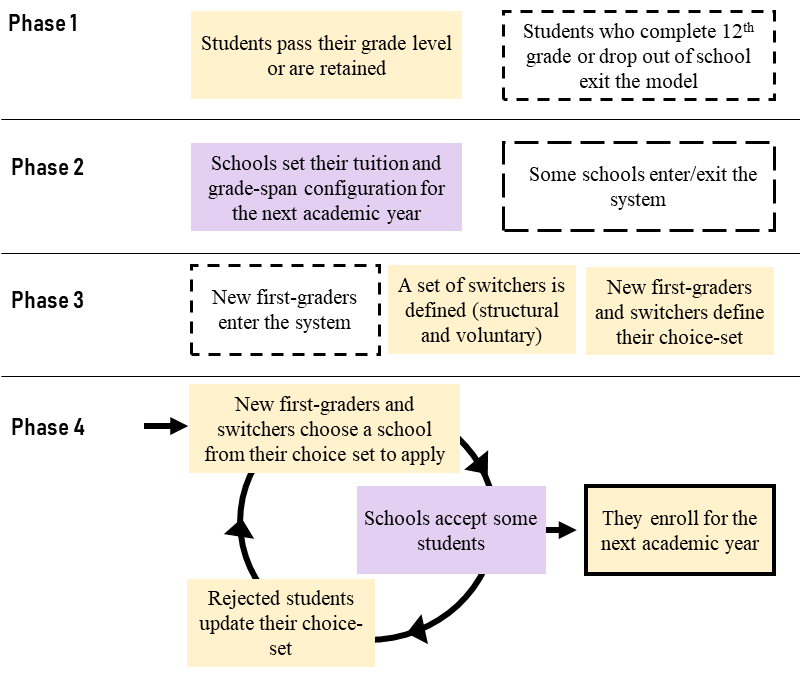
Phase 1. Students experience an academic year
Students update their achievement in time \(t\) (\({A_{i,t}}\)) following Equation 1. Their achievement level depends on their previous achievement (\({A_{i,t-1}}\)), the value-added of their current school (\({VA_j}\)), the parameters \({\alpha_{ach}}\) and \({\beta_{ach}}\), and a random error \({\epsilon_{ach}}\).
| \[ A_{i,t}=\alpha_{ach}+\beta_{ach}A_{i,t-1}+VA_j+\epsilon_{ach}, \epsilon_{ach}\sim N(0,s_{ach}^2)\] | \[(1)\] |
Very low-achieving students are not promoted to the next grade - at each grade level, schools retain \(r\%\) of students. Students are also at risk of dropping out of school, with a probability that depends on their grade level and whether or not they were retained (See Appendix A, Equation 5 for details). Students who are promoted in the 12th grade and students who drop out exit the system.
Phase 2. Schools define their offerings for the next academic year
Schools that charge tuition update their monthly tuition. The fee charged by a school \(j\) from sector \(s\), will be updated by following Equation 2, where \({\alpha_{Ts}}\) and \({\beta_{Ts}}\) are parameters that depend on the school’s sector, and \({\epsilon_{Ts}}\) is a random error whose distribution depends on the school’s sector.
| \[ Fee_{j,s,t}=\alpha_{Ts}+\beta_{Ts}Fee_{j,s,t-1}+\epsilon_{Ts}, \epsilon_{Ts}\sim N(0,s_{Ts}^2)\] | \[(2)\] |
Additionally, for any given year, schools in the actual data that entered and exited the system, or changed their grade-span configuration, also do so in the simulation.
Phase 3. Students identify and evaluate potential schools
Three categories of students must look for a school to enroll: 1) Students whose current school does not offer their next required grade level or their school closed (structural switches). 2) New students entering the system, which will enroll in first grade for the first time. 3) Students who decide to leave their current school even if they have the option to stay (voluntary switches). The probability that a student does so is given by the switching probability, \(sp_{s,rs}\), and depends on the student’s school sector, \(s\), and retention status, \(rs\) (See details in Appendix A, Phase 3). Students who do not switch schools enroll in their current school for the next academic year. This allows schools to update their available capacity for each grade level.
Students looking for a school define a choice-set of schools they will explicitly consider as an option. This follows the model from Canals et al. (2022), where a student becomes aware of schools in three ways: They receive public information about schools, which depends on each school’s propensity to be known through public information (\(p_j\)). They become aware of schools located at a distance \(T\) km or less from their home. They gather information from their social network, becoming aware of the previous schools of students to which they are connected. To do so, each student becomes directly connected with \(n\) other students7. They are more likely to become connected with students whose parents have similar educational levels, a tendency governed by a parameter \(\theta\) (Detail in Appendix A, Equation 10). A student’s choice-set is then defined as all the schools of which they are aware that offer the grade level they require and that they can afford.
Students calculate the propensity to choose each school from their choice-set, which can be considered a measure of the relative desirability of each school and depends on several variables. It is important to note that schools’ value-added is not observable by students, and thus, they do not consider it directly when choosing a school. Instead, students can observe the mean achievement of the school’s students, which can be thought of as a publicly available mean score for a school on a standardized achievement test. Such a measure can affect the relative desirability of a school for a given student.
Students are categorized into classes with different preferences. The propensity of student \(i\), in preference class \(c\), to prefer school \(j\) from its choice-set is given by Equation 3, and depends on the distance from home to school (\(D_{ij}\)), the difference between the educational level of their household and the school’s households (\(SD_{ij}\))8, mean achievement of the school’s students (\(MA_{j}\)), school selectivity (\(Sel_{j}\)), a variable indicating whether someone in their social network attends said school (\(SP_{ij}\))9 and a variable indicating whether the school’s grade-span configuration allows a primary school student to finish secondary education in the same school (\(FS_{ij}\)). \(\beta_{3}\),\(\beta_{4}\), \(\beta_{5}\) and \(\beta_{6}\) are coefficients with equal value for every student, and \(\beta_{c1}\) and \(\beta_{c2}\) vary depending on the student’s preference class.
| \[ V_{i,c,j}=\beta_{c1}D_{ij}+\beta_{c2}MA_{j}+\beta_{3}FS_{ij}+\beta_{4}Sel_{j}+\beta_{5}SP_{ij}+\beta_{6}SD_{ij}, c \in {1,2}\] | \[(3)\] |
Phase 4. Students apply to schools and schools select applicants
The following application and enrollment processes are repeated until everyone is enrolled:
- Students apply to one school of their choice-set, which is probabilistically selected based on their propensity to choose the schools from the set. The probability of school \(j\) in choice set \(CS_i\) of being chosen by student \(i\) is proportional to their desirability and given by Equation 4.
\[ P[i \; apply \; to \; j \mid j \in CS_i] = \frac{e^{V_{i,c,j}}} {\sum_{l \in CS_i} e^{V_{i,c,l}} } \] \[(4)\] - Schools select students from among their applicants. Non-selective schools consider all applicants eligible, while selective schools only consider those that meet their academic requirements. Schools with enough capacity accept all the eligible applicants; schools with not enough capacity choose among them. In the case of non-selective schools, this selection is modeled as a random sampling, while selective schools select students with a probability proportional to the student’s achievement level.
- Students who did not find a school discard the school that rejected them from their choice-set.
If by the end of the process, there are unenrolled students with empty choice sets, they are enrolled in schools using a process described in Appendix A (Phase 4, step 4).10
Data
We used school, student and block datasets to initialize, calibrate and validate the model for four Chilean cities, all of which experienced a decrease of the public enrollment between 2004 and 2016: Salamanca, Vallenar, Punta Arenas, and Osorno. Table 1 summarizes some characteristics of the cities in those years, evidencing important variations in the public school enrollment decay, size, and socioeconomic characteristics11.
The model was initialized using data for the year 2004, but for calibration and validation purposes, we used 2004-2016 data12. The Ministry of Education of Chile provided school and student administrative data, and also data from the Survey of School Choice 2016 (Encuesta de Elección Escolar 2016). Agencia de Calidad de la Educación (the Chilean Educational Quality Agency) provided the SIMCE datasets, containing standardized achievement test scores, socioeconomic variables, and other students’ and schools’ characteristics. Information about the cities’ blocks or groups of blocks comes from the National Population and Housing Census conducted by the National Institute of Statistics of Chile (INE, by its Spanish acronym).
| City | Osorno | Punta Arenas | Vallenar | Salamanca | |||||
|---|---|---|---|---|---|---|---|---|---|
| Region | Region de los Lagos | Región de Magallanes y de la Antártica Chilena | Región de Atacama | Región de Coquimbo | |||||
| Year | 2004 | 2016 | 2004 | 2016 | 2004 | 2016 | 2004 | 2016 | |
| Total enrollment1 | 31,035 | 27,399 | 24,025 | 20,744 | 11,566 | 9,647 | 3,066 | 3,585 | |
| Enrollment in 1st grade1 | 2,396 | 2,245 | 1,905 | 1,815 | 828 | 870 | 200 | 278 | |
| Average parents' schooling years2 | 6.8 | 12.2 | 7.2 | 13.1 | 7.1 | 12 | 7 | 11.6 | |
| Percentage of economically disadvantaged students1 | 48.1 | 26.1 | 59.6 | 46.6 | |||||
| Total number of schools1 | 69 | 69 | 41 | 41 | 21 | 21 | 8 | 10 | |
| Schools by sector (%)1,3 | Public schools | 30.4 | 30.4 | 58.5 | 56.1 | 81 | 81 | 25 | 30 |
| Private voucher schools | 63.8 | 63.8 | 24.4 | 29.3 | 14.3 | 14.3 | 75 | 70 | |
| Private fee-paying schools | 5.8 | 5.8 | 17.1 | 14.6 | 4.8 | 4.8 | 0.0 | 0.0 | |
| Enrollment by sector (%)1 | Public schools | 51.3 | 38 | 60.3 | 50 | 80.3 | 74.4 | 58.4 | 19.6 |
| Private voucher schools | 40.8 | 52.2 | 28.2 | 37.6 | 17.8 | 22.4 | 41.6 | 80.4 | |
| Private fee-paying schools | 7.9 | 9.9 | 11.4 | 12.5 | 2 | 3.2 | 0.0 | 0.0 | |
| Standardized achievement test scores by sector2,4 | Public schools | -0.04 | -0.02 | -0.24 | -0.31 | -0.13 | -0.32 | 0.1 | -0.71 |
| Private voucher schools | 0.09 | 0.11 | 0.37 | 0.06 | -0.24 | 0.43 | 0.17 | -0.2 | |
| Private fee-paying schools | 1.12 | 0.84 | 0.45 | 0.52 | 1.24 | 1.27 | |||
| Public schools by grade-span configuration (%)1 | Only primary education | 71.4 | 71.4 | 70.8 | 65.2 | 76.5 | 76.5 | 50 | 66.7 |
| Only or mostly secondary education | 23.8 | 28.6 | 29.2 | 26.1 | 17.6 | 23.5 | 50 | 33.3 | |
| Both primary and secondary education | 4.8 | 0 | 0 | 8.7 | 5.9 | 0 | 0 | 0 | |
| Private voucher schools by grade-span configuration (%)1 | Only primary education | 59.1 | 54.5 | 30 | 16.7 | 33.3 | 33.3 | 66.7 | 28.6 |
| Only or mostly secondary education | 22.7 | 11.4 | 10 | 0 | 0 | 0 | 0 | 0 | |
| Both primary and secondary education | 18.2 | 34.1 | 60 | 83.3 | 66.7 | 66.7 | 33.3 | 71.4 | |
| Private fee-paying schools by grade-span configuration (%)1 | Only primary education | 0 | 0 | 14.3 | 0 | 0 | 0 | ||
| Only or mostly secondary education | 0 | 0 | 0 | 0 | 0 | 0 | |||
| Both primary and secondary education | 100 | 100 | 85.7 | 100 | 100 | 100 | |||
Model calibration
The parameters were calibrated using data at the school-, student-, or block-levels. Sector-level variables -which were used for model validation- were not used to calibrate the model. The calibration process was carried out separately for each city. Appendix C provides details about the calibration processes for the parameters of each of the model rules, the specific datasets used, and the parameters found for each city. We provide an overview below.
Equations 1, 2, and 3, were calibrated by estimating statistical or econometric models. Equation 1, that governs student achievement progression, was estimated with hierarchical linear models using data of students’ scores in the SIMCE tests taken in the 4th, 8th and 10th grade levels. Equation 2, which models school tuition changes, was estimated through autoregressive models using schools’ tuition information included in administrative datasets. Equation 3, which gives student preferences for schools, was estimated through a latent class logit model using data from the Survey of School Choice 2016, where parents listed the schools they were aware of and their most preferred schools. The latent class logit model also identified membership to the preferences classes used in Equation 3 (See Appendix B, Equation 19).
The probabilities of switching schools for students who could have attended their next grade level in the same school (\(sp_{s,rs}\)) and the percentage of retained students (\(r\)) were calculated directly from the data. We used administrative longitudinal data to make yearly calculations, and then averaged them into a single value. The distance threshold for being aware of schools (\(T\)), the number of connections in students’ social network (\(n\)), and the propensity for those connections to be to other students with similar EL (\(\theta\)), were calibrated by optimizing a version of the model the was initialized with actual students from 2016. A genetic algorithm was used to choose values that minimized the difference between the choice sets simulated by the model and the actual choice-sets reported by students in the Survey of School Choice 2016 (Canals et al. 2022).
Model validation
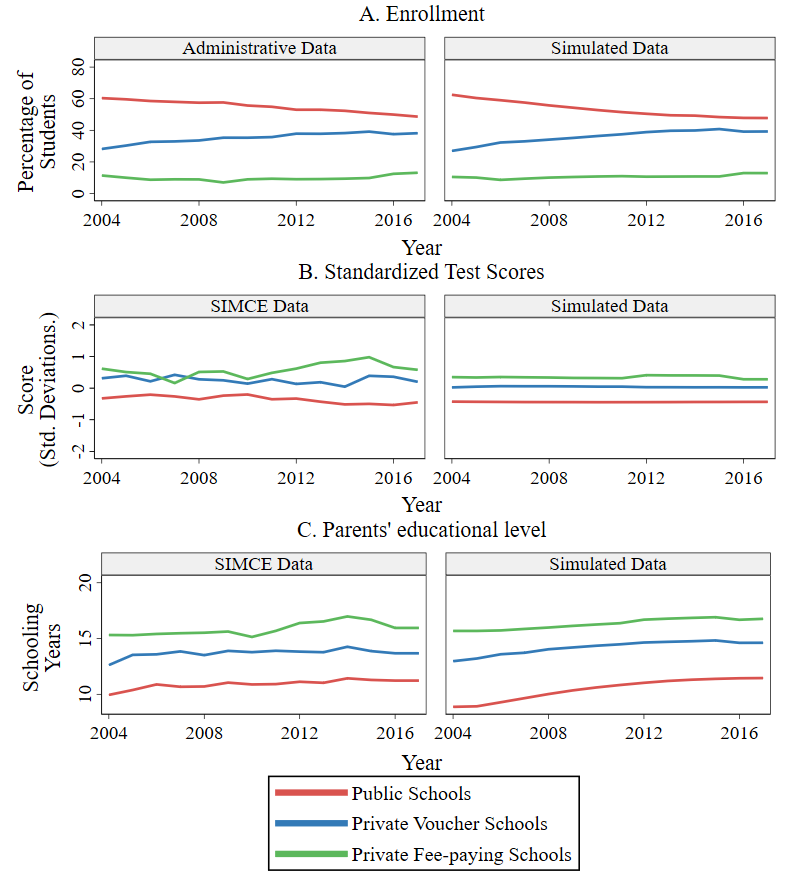
Once the model was calibrated for each city, we validated it by examining how well its output matched the temporal trends of three variables that were not part of the calibration: school sectors’ enrollment, standardized achievement test scores13, and EL (measured in parents’ schooling years). For that purpose, we initialized the model in the year 2004 and ran 300 simulations covering the period from 2004 to 2016; we call these simulations baseline scenario. Then, we compared the empirical trends of these variables to the simulated baseline scenario by school sector. Note that each of the three variables used for matching purposes are aggregate estimations that do not depend on a single model rule; instead, they depend on the interaction of many of them, such as the process of families becoming aware of schools, families applying to schools, schools’ selecting applicants, among others. Note also that each of those model rules was independently calibrated, and without using aggregated variables by sector as a reference.
Figure 4 portrays the trends of these three variables for the city of Punta Arenas, using average values across the 300 model runs. The figure demonstrates that the average behavior of the model represents the general patterns quite well, albeit with some differences in magnitude and smoothness. This confirms that the model achieves relational equivalence, effectively reproducing the relationships observed in reality. To see other cities’ trends, please refer to the trend plots available in Appendix D.
Experiments
To examine the role of the elements identified above in shaping public sector enrollment, for each of them, we designed one or two experiments that modify selected aspects of the baseline scenario. This resulted in 10 total simulation scenarios, including the baseline. For each city and experiment, we ran 300 simulations for the period 2004-2016; this comprised almost 12,000 model runs14. We then analyzed the experimental output by calculating the deviation between the public enrollment decrease in the baseline and each counterfactual scenario. A brief description of the simulation experiments conducted is presented below. Appendix E includes further details about how each experimental scenario was modeled.
Element 1: Entry of new schools
- Experiment 1: No change in the number of schools by sector. The number of schools by sector remains stable since 2004, with no school entry and exit to the school system.
- Experiment 2: Public sector reacting to demand. Every year, a new public school is opened in the most deprived area of the city.
Element 2: Academic performance of public schools
- Experiment 3: Public schools decreasing their value-added. Every public school decreases its value-added by 0.03 standard deviations per year.
- Experiment 4: Public schools increasing their value-added. Every public school increases its value-added by 0.03 standard deviations per year.15
Element 3: New primary students entry
- Experiment 5: No change in the number of students entering to the school system. The number of students entering first grade remains stable since 2004.
Element 4: Mean-tested vouchers
- Experiment 6: Non-Implementation of SEP Program. No schools sign into the SEP Program during the whole period.
Element 5: Grade-span configuration of schools in each sector
- Experiment 7: Stable educational levels offered by schools. Schools do not change their grade-span configuration over time.
- Experiment 8: Coordination of public schools to offer primary and secondary education. Each primary public school establishes a partnership with a nearby public secondary school. This partnership guarantees that students who successfully complete the highest grade level offered at the primary school are promptly enrolled in the next grade level at the secondary school.
Element 6: Population’s SES trends
- Experiment 9: Stable socioeconomic status of the population. The average population’s EL and the geographic distribution of the population remain unchanged over time16.
Simulation analysis
To compare the different elements, for each experiment \(i\), we estimated the Public Enrollment Difference between 2004 and 2016 \(PED_i\). Being \(pe_{2004}\) and \(pe_{2016}\) the percentage of public enrollment in 2004 and 2016, respectively, \(PED_i=pe_{2016}-pe_{2004}\), indicating the percentage points (p.p.) that the public enrollment varied during the specific period. In the baseline scenario (BE), which mirrors the real trends, Osorno, Punta Arenas, Vallenar and Salamanca experience a public enrollment variation (\(PED_{BE}\)) of -10.9, -14.6, -6.8 and -28.7 p.p., respectively. We assessed the impact of each experiment on public enrollment, measured as \(I_i=PED_i-PED_{BE}\).
Results
Analysis of the elements driving public school enrollment
Figure 5 illustrates the impact \(I_i\) of each simulation experiment on public enrollment for each city. Considering that in the baseline scenario the public enrollment decreased in all the cities, \(I_i>0\) indicates that the experiment resulted in an increase in public enrollment or a less pronounced decay compared to the baseline scenario. Conversely, \(I_i<0\) indicates that the experiment led to a greater decrease in public enrollment compared to the baseline scenario. Refer to Appendix F to see the impact on private enrollment, to Appendix G to see enrollment differences between 2004 and 2016 by school sectors and to Appendix H to see public enrollment trends by experiment over time.
Figure 5 shows that, in general, the grade-span configuration of schools in each sector (Element 5) has the greatest effect on public enrollment, although with variation across cities. A policy design where public schools coordinate to guarantee a seat at a public secondary school for students graduating from a public primary school, as it is represented in E8, is the experiment that impacts the public enrollment decrease the most in the simulations for Osorno and Vallenar (10.9 and 3.9 p.p. of impact, respectively). In the simulations for Punta Arenas, it is the experiment with the second biggest impact (7.0 p.p.) and for Salamanca, has a rather large impact (10.4 p.p.). These impacts reflect an important reduction in the public enrollment drop. In fact, under this simulated scenario, the public enrollment in Osorno remained stable during the period 2004-2016, instead of dropping by 10.9 p.p. as in the baseline scenario; in Punta Arenas and Vallenar, the drop was around half that of the baseline scenario (7.6 and 2.9 p.p. drop in E8 and 14.6 and 6.8 p.p. in the baseline scenario, respectively); and, in Salamanca, the public enrollment decreased 18.3 p.p., quite less than in the baseline scenario (28.7 p.p.).
The other experiment related to this element, E7, where the educational levels offered by the schools remained stable between 2004 and 2016, is the experiment that had the largest impact on public enrollment for Salamanca (23.2 p.p.), producing a 5.5 p.p. public enrollment drop versus a 28.7 p.p drop observed in the baseline scenario. In the simulations for Osorno and Punta Arenas, E7 is the experiment with the second and third biggest impact on public enrollment (impact of 5.5 and 3.3 p.p., respectively). E7 has only a marginal effect in the simulation for Vallenar. This is likely because Vallenar is the only city where the share of private voucher schools offering both primary and secondary education did not increase over time in the period analyzed (see Table 1).

Figure 5 also shows that the socioeconomic composition of the population (Element 6), had a substantial effect on public enrollment. Experiment E9 simulated what would have happened if the SES of the population in each city, instead of increasing over time, had remained stable. In our simulations for Punta Arenas, the city with the population with the highest SES -i.e., highest EL and lowest proportion of economically disadvantaged students (see Table 1), E9 is the experiment that most impacted public enrollment. Public enrollment in Punta Arenas under this scenario dropped 3.0 p.p. instead of 14.6 p.p. (I =11.6 p.p.). In the simulations for Osorno and Vallenar, the SES of the population is the element that generated the highest impact aside from grade-span configuration (I =4.5 and I =1.7 p.p., respectively). In Osorno this corresponds to a reduction of the public enrollment 6.4 p.p. compared to the baseline scenario of 10.9 p.p.; in Vallenar, a reduction of 5.1 p.p. compared to a baseline of 6.8 p.p. For Salamanca, this experiment has almost zero impact. The likely explanation for this is that Salamanca is the only city where every school is free of charge, making even the students with the tightest budget constraint able to attend private voucher schools. Therefore, an increase in population SES has practically no effect.
The entry of new schools (Element 1) had effects that widely varied across cities. Surprisingly, in the simulations for Punta Arenas, where the percentage of private voucher schools is higher in 2016 compared to 2004 (see Table 1), E1 and E2 generated only small effects. This is also true for Vallenar, where the percentage of schools by sector was the same in 2004 and 2016. In contrast, the simulations for Salamanca and, to a lesser extent, Osorno, exhibited changes in enrollment trends in experiments E1 and E2. In Salamanca, a small town with few schools (see Table 1), the number of schools by sector is the second most important element affecting public enrollment. In the scenario with a public sector that reacts to the demand by opening new schools (E2), public enrollment decreased 15.7 p.p., quite less than in the baseline scenario of 28.7 p.p. (I = 13.0 p.p.). Meanwhile, in the scenario where the number of schools by sector does not change over time (E1), the impact is 4.9 p.p.. In Osorno, the impact of Element 1 is observed in the experiment where the public sector reacts to demand (E2), producing an impact of 2.7 p.p.
The generally small impact of the increase of new public supply (E2) in most cities can best be understood by considering all the conditions that must be met for enrollment in a new school. As a result, a small number of students enter a new school in its first year. Taking for example the city of Osorno, in 2005 -the year when the first new public school was opened in this experiment- 23% of the students across all the runs were looking for a new school (first graders and students switching schools). Of those, only 2% included the school in their choice-set17 and 1% applied to it and got accepted.
The reasons for not observing impacts in Vallenar and Punta Arenas require considering the details of each context. In the case of Vallenar, the public enrollment is already at a very high level, making a substantial percentage increase less likely. In Punta Arenas, the small effect of increasing public school supply is likely related to its size and socioeconomic composition. Punta Arenas is larger than Vallenar and Salamanca, so a smaller percentage of students become aware of each new school as it enters. The population in Punta Arenas also has a higher SES when compared to Osorno, making it less willing to move towards the public school sector (see Table 1).
Variations in public schools’ academic performance (Element 2) also affected public enrollment, but with an effect of less than 1.5 p.p. in most cases. The only exception is the simulation for Salamanca, where an increase in public schools’ value-added (E4) produced a public enrollment drop of 17.0 instead of 28.7 p.p. producing an aggregated impact of 11.7 p.p. This might be related to the fact that the initial difference between private vouchers’ and public schools’ standardized test scores was smaller for Salamanca than the other cities (see Table 1), and thus when incrementing their value-added public schools became ‘good schools’ relative to private-voucher ones sooner.
Regarding the new primary student entry to the school system (Element 3), the cities had experienced a diversity of trends in the actual 2004-2016 data (see Table 1). Osorno and Punta Arenas are cities where the number of students entering the school system decreased over time, while the opposite happened in Vallenar and Salamanca. Regarding the magnitudes, Osorno, Punta Arenas, and Vallenar only experienced small changes, while Salamanca experienced a much larger change (39%, see Table 1). Consequently, when these trends were compared to E5 that held the population constant, a meaningful impact was only observed for Salamanca (I=-3.8 p.p.).
Finally, the introduction of means-tested vouchers (Element 4), has only a tiny effect on public enrollment in the simulations for Osorno, Punta Arenas, and Vallenar (with E6 producing impacts between -1 and 1 p.p.), suggesting that the SEP program did contribute substantially to the public enrollment decline. Like with the impact of new public school entry, this is probably related to the number of students whose school choice decisions can be impacted in any given year. By definition, the SEP program is only targeted to a subset of all students. Taking the example of Punta Arenas in the baseline scenario, in 2008, the year when the program started, 28% of simulated students were economically disadvantaged, but only 22% of those were looking for a school that year. This implies that among the entire student population 6% were disadvantaged students who engaged in the school search process. Of that 6%, 31% included at least one private voucher school participating in the SEP Program in their choice-set, and 7% applied and got accepted in one of them. Taking into account that the program started in 2008, it is difficult to observe a large aggregate impact by 2016.
Boundary conditions
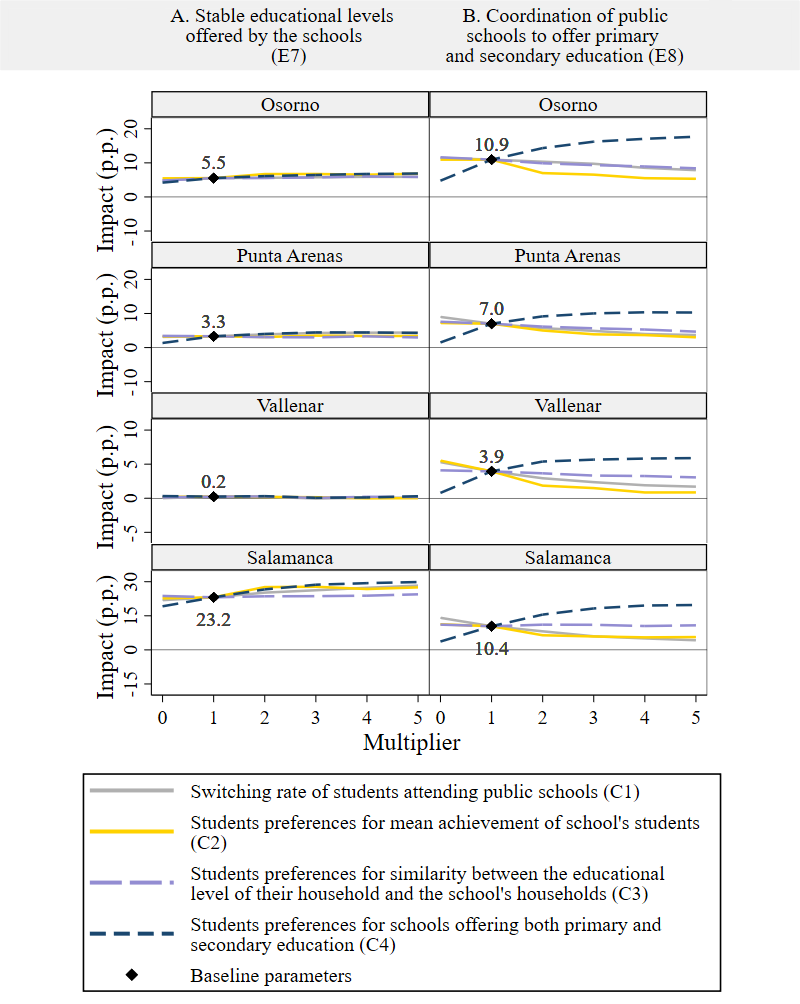
The most notable element affecting public enrollment in our simulation is the grade-span configuration of schools in each sector (Element 5). In what follows, we attempt to identify the conditions where that is no longer true in the model – i.e., the conditions for which the two experiments that feature grade-span configuration as the primary element, E7 and E8, do not produce an impact on public sector enrollment. In general, we find that the impact of grade-span configuration of schools on public school enrollment is very robust to a wide variety of changes chosen with the purpose of eliminating it.
Specifically, we considered additional experimental conditions, where we modified one of four model parameters at a time: the switching rate of students attending public schools (condition C1), the students’ preference regarding the mean achievement of school’s students (condition C2), their preference for the proximity between their parents’ educational level and that of the school’s students (condition C3), and their preference for schools offering both primary and secondary education at the same school (condition C4). In each condition, we changed the relevant parameter in the baseline scenario by multiplying its baseline value by 0, 2, 3, 4, or 5 to nullify or amplify its effect, and recreated the baseline scenario leaving all other parameters the same. To distinguish this altered baseline scenario from the actual baseline scenario for a set of conditions, we refer to it as Experiment 0 (E0). For example, the switching probably in Osorno for retained students in the public sector, \(sp_{p,r}\), in the baseline scenario is 0.308 (Appendix C, Table 4). As part of our analysis of condition C1, we created five alternative values of this parameter, one for each multiplier. This resulted in five corresponding E0 scenarios that could be used as the baseline comparison group when re-running experiments E7 and E818. For every condition, we conducted 300 runs of E0, and experiments E7 and E8. This resulted in 18,000 additional simulation runs (300 runs \(\cdot\) 3 experiments \(\cdot\) 5 multipliers \(\cdot\) 4 modified parameters). Figure 6 shows those results.
The results for experiment E7 are robust to even extreme changes in the assumptions about C1-C4. For example, even when there is no preference at all for schools offering both primary and secondary grade levels (0 multiplier, C4), the final 12-year impact on public enrollment decline remains positive. The only city where the impact fell below 0 is Vallenar (I=-0.04, for multiplier 3, C1 and I=-0.02 for multiplier 4, C2). However, this is a city where the educational levels offered by the schools only changed a little over time (see Table 1), so the impact in the baseline condition (multiplier 1, C1-C4) was very small to begin with.
The impacts also remain positive across conditions C1-C4 for experiment E8, but the variance in impacts across assumptions is much greater. As the switching rate increases (C1), students place more emphasis on schools’ mean achievement (C2) and the proximity between their parents’ educational level and that of the school’s students (C3), the smaller the impact of coordinating primary and secondary grades in the public sector. On the other hand, the more students value the schools offering both primary and secondary education (C4), the larger the impact. Nullifying that preference however (0 multiplier, C4), does not eliminate the positive impact of public sector coordination to offer both educational levels (4.8, 1.5, 0.8 and 3.7 p.p. of impact for Osorno, Punta Arenas, Vallenar and Salamanca, respectively, experiment E8). Similarly, a high switching rate can reduce the impact of the coordination of the public sector on the public enrollment decline, but still, even having five times more students in the public sector deciding to switch (5 multipliers, C1) cannot suppress the impact of this measure.
Discussion
To gain a deeper understanding of the consequences of school choice policies on public school enrollment, it is essential to disentangle the simultaneous mechanisms at play. Educational systems are complex (Ghaffarzadegan et al. 2017; Jacobson et al. 2019; Maroulis et al. 2010), making it hard to isolate the different contextual and policy design features that may affect public school enrollment trends. To overcome this obstacle, and aligned with the literature that uses calibrated agent-based models to study the primary and secondary education system (Díaz et al. 2019; Harland & Heppenstall 2012; Maroulis et al. 2014; Maroulis 2016; Millington et al. 2014), we developed an agent-based model grounded in the context of Chile, a country with an extensive and longstanding voucher policy. Our empirically grounded ABM provided a realistic representation of the Chilean educational system, enabling us to reach concrete conclusions about this particular case. By simulating the interacting factors that impact school enrollment over time, our model also allowed us to delve into a historical pattern of a controversial subject in Chilean education: the decrease in public school enrollment. Moreover, by calibrating the model separately to multiple cities, our approach allowed us to illustrate how the same mechanisms can differently impact different contexts.
Our study contributes to interpreting the public enrollment decline in Chile in multiple ways. First, we add a new structural consideration – differences in the school grade-span configuration by sector – to existing explanations for the decline of public school enrollment in Chile. In fact, our model suggests that changes in grade span configuration would likely have been the most effective factor in reducing the decline in public school enrollment in the Chilean cities we consider in the analysis. This conclusion is not only based on the importance of this element in our simulation experiments, but it is also consistent with the observed behavior of schools during the period analyzed. In contrast to public schools that face many restrictions and difficulties in expanding their supply (Bellei et al. 2010), many private voucher schools began offering the full range of grade levels instead of only primary or secondary education between the years of 2004 and 2016. Moreover, this disparity was likely exacerbated by an amendment to the JEC law approved in 2004 that allowed schools to use competitive public funds to expand the educational levels they offered. The allocation decision for these funds included a favorable assessment of infrastructure projects to which the applicant school also contributed with its own resources. Consequently, although public schools could also have applied for the funding, their ability to secure fund awards may have been limited.
Our finding about the relevance of the grade-span configuration of schools of each sector is aligned with the study of Juneja (2007) for the case of India. She pointed out that the families’ preference for schools offering both primary and secondary education at the same school can contribute to a lower public school enrollment, especially in contexts where most of the secondary school supply is private. We add to that insight by demonstrating that even in contexts without such a preference, the degree of coordination between primary and secondary public school supply can still have a meaningful impact on public school enrollment. This is because grade-span configuration governs the timing when most families choose schools. As fewer public schools offer both educational levels, students from those schools are more frequently forced to switch schools, generating more opportunities to choose a different school sector. At the same time, schools offering only secondary education may struggle to attract students who are already enrolled in another school that offers the full range of grade levels. Thus, bridging the provision of primary and secondary education – either by providing both educational levels in the same school or by creating a coordination mechanism between primary and secondary schools – is a potentially powerful action that school sectors can use to attract and retain students.
Second, our analysis also highlights that there is not a single explanation for the aggregate public enrollment decline observed in Chile. Instead, the impact of the school choice policy on public enrollment depends on a combination of policy design features and contextual characteristics. This is evidenced by the fact that only changing one element at a time in our simulations cannot account for the entire public enrollment decline in Chile. For example, with respect to explanations related to the demand for public schooling, previous research about the Chilean case has suggested that there has been a decrease in public schools’ appeal and quality affecting public enrollment (Raczynski et al. 2010; Zapata 2010). It has also been argued that relative demand for public schools may have decreased on account of a decrease in the number of students entering primary education (Núñez et al. 2015). Our simulations isolating the role of the elements related to those explanations – academic performance of public schools (Element 2) and the new primary students entry (Element 3) – imply that each of those elements alone is not a robust driver of the public enrollment trends.
Furthermore, the most important factor in determining public school enrollment, other than grade-span configuration of the schools, likely varied across cities. Our simulation experiments suggest that the population’s SES trends (Element 6) were likely an important factor in a city like Punta Arenas, which reached a higher socioeconomic status, while the entry of new schools (Element 1) was likely a more important element in Salamanca, a smaller city. This diversity across cities underscores how the aggregate trends observed in Chile result from complex processes happening at different places, each characterized by distinct sizes, initial states, and population trends, all of which help produce effects of varying magnitude.
Third, our study aligns with existing research on the Preferential School Subsidy Reform (SEP), which transformed the flat voucher system into a means-tested one. Prior research has found small or null effects of this policy on public school enrollment (Centro de Estudios MINEDUC 2015; Flores 2020; Navarro-Palau 2017). In our simulations, we did not observe much of an effect of the introduction of the SEP Program. It is hard for a policy affecting only a fraction of students to significantly influence aggregate enrollment trends.
In interpreting the findings of our study, it is necessary to note an important limitation. Although our analysis of the boundary conditions in Figure 6 indicates that grade-span configuration is likely a generally applicable mechanism affecting enrollment trends, caution is warranted in extrapolating to contexts outside of Chile. Nonetheless, our findings have implications for future research. In particular, given the magnitude and persistence of the effect of the grade-span configuration of each sector suggested by our model, at a minimum, it is important for future research to take this institutional feature into account when examining the reasons for differences in educational enrollment across sectors, and school choice decisions.
Additionally, our identification of the importance of grade-span configuration suggests a rather straightforward and inexpensive prescription for those concerned with strengthening public sector enrollment in Chile, as well as other school systems that have implemented school choice reforms: the creation of a formal mechanism for coordination among primary and secondary public schools to ensure students graduating from public schools a seat at a secondary public school. One could view such a mechanism as analogous to policies that attempt to “nudge” behavior by changing the architecture of choice without restricting the ability to choose (Grimmelikhuijsen et al. 2017; Tummers 2022). Families could still apply to the secondary school of their choice but with the security of a guaranteed option.
Regardless of the specific policies pursued, our study illustrates that any policy prescription within a school choice system aimed at strengthening public school enrollment will likely take time. In almost all our simulation experiments, enrollment changes were gradual. This is because the proportion of families switching schools or choosing a school for the first time is small in any given year, creating an inertia in the school system. This inertia can give policymakers time to react to the trends observed in the school system, but it also requires paying close attention to incremental changes that can accumulate into larger ones over time.
Lastly, our model could serve as a starting point for other public policy analyses. As we pointed out earlier, since 2015, Chile has implemented several structural reforms, aiming to reduce the role of the market in education (Bellei & Munoz 2023; Cummings et al. 2023). Other researchers can easily modify our model to represent the changes introduced by these reforms - such as banning student selection and charging tuition at private voucher schools- and projecting their long-term consequences.
Acknowledgements
The authors acknowledge the support from (i) the National Agency for Research and Development (ANID) / Scholarship Program / DOCTORADO NACIONAL/ 2017 – 21170290, (ii) the ANID/PIA/Basal Funds for Centers of Excellence FB0003, and (iii) the ANID / FONDECYT Postdoctorado Nacional 2024 / N° 3240004. This research was also partially supported by (iv) the supercomputing infrastructure of the National Laboratory for High Performance Computing Chile (NLHPC, ECM-02) at the Faculty of Physical and Mathematical Sciences, Universidad de Chile, and (v) the high-performance computing infrastructure from Research Computing at Arizona State University. Their contribution is gratefully acknowledged.
This research used the SIMCE data set, coming from the Agencia de Calidad de la Educación, from Chile, schools’ and students’ data coming from the Chilean Ministry of Education, and block’s data coming from the National Institute of Statistics of Chile (INE) as data sources. We thank these three institutions for providing access to this information. All the outcomes of the study are the sole responsibility of the authors and do not reflect the opinion of the mentioned institutions.
Finally, we would like to thank the anonymous reviewers, the participants at the 2024 ASU CTDS HYU C2S2 International Mini-Conference, the 2023 Center for Advanced Research in Education (CIAE) Seminar series at Universidad de Chile, the 2021 Social Simulation Conference, the 2021 WERA Virtual Focal Meeting and the 12° Yearly meeting of the Sociedad Chilena de Políticas Públicas (Public Policy Society of Chile) for their valuable comments.
Appendix A: Model Description
We developed an ABM that represents a city’s school system using the Netlogo multi-agent programmable modeling environment v. 6.2.1 (Wilensky 1999). The model consists of students and schools located on a grid that represents the geography of a particular city. The city area is divided into patches, small squares representing smaller geographic areas. Patches have two attributes: population and EL. Students and schools have different attributes detailed in the main text (see Methods, Model Section). The model requires Geographic Information System (GIS) input data of schools and city areas (blocks or groups of blocks) to initialize and update some schools’ and students’ characteristics.
Each time period of the model represents one year. Each year, the students and schools make decisions and experience changes based on the rules and conditions articulated below. The model simulates the dynamics driving school enrollment for the period 2004-2016. Each iteration includes five phases; each of them involves several processes.
Phase 1. Students experience an academic year
- Students update their achievement following Equation 1. The resulting achievement level is bounded within the interval [-4, 4].
- Schools grade their students. In each grade level, they promote to the next grade level the \(1-r\) of students with the highest academic achievement.
- Students who passed 12th grade level graduate and disappear from the model.
- Some students dropout probabilistically, depending on their grade level (\({g_i}\)) and whether they have passed or failed. The probability of school dropout is given by Equation 5, where \({\alpha_{pass}}\), \({\alpha_{fail}}\) and \({\beta_{fail}}\) are parameters. Students that dropout disappear from the model.
\[ P[dropout] = \left\lbrace \begin{array}{ll} \alpha_{pass} & if \; student \; passed \\ \alpha_{fail}e^{g_i\beta_{fail}} & if \; student \; failed \end{array} \right. \] \[(5)\]
Phase 2. Schools define their offerings for the next academic year
- Schools that charge tuition update their monthly tuition by following Equation 2. The new tuition is then bounded to the range [0,50] in the case of public schools, [0,100] in the case of private voucher schools and [0,500] in the case of private fee-paying schools. Tuition-free schools keep their tuition at 0.
- Some schools open and close. If a school closing date in the school input data matches the simulated year, the school closes, disappearing from the model; if its opening date matches the forthcoming year, the school appears in the model.
- Some schools change the educational levels they offer. Based on model input data providing the sequence of the school’s grade-span configuration, the schools update their educational levels offered if the forthcoming year’s grade-span configuration is different from the current one.
Phase 3. Students identify and evaluate potential schools
- Students promoted to a grade level that is not offered by their current school or whose school closed, set their current school as an empty variable.
- Some students decide to leave their current school even if they have the option to stay. The probability that a student does so is given by a switching probability \(sp_{s,rs}\) that depends on the students’ school sector, \(s\), and retention status \(rs\). Specifically, we distinguish three retention statuses: students who were retained, students who were promoted in 8th grade (the last grade level of primary education), and students who were promoted in any other grade. The switching probability values \(sp_{s,rs}\) vary for each of these three groups within each of the three sectors, resulting in a total of 9 different values (3 groups \(\cdot\) 3 sectors). Students who decide to switch set their current school as an empty variable, while those who do not, keep their current school as it is.
- New students who will enter first grade next year appear in the model. Their number is a function of time \(t\), and it is obtained by estimating Equation 6, where \({\beta_{ns0}}\), \({\beta_{ns1}}\) and \({\beta_{ns2}}\) are parameters, and \({\epsilon_{ns}}\) is a random error. The value obtained by that equation is then multiplied by \(p_{sample}\) – a parameter indicating the percentage of the students’ population of the city that is simulated in the model- and rounded.
\[ ns=\beta_{ns0}+\beta_{ns1}(t+1)+\beta_{ns2}{(t+1)}^2+\epsilon_{ns}, \epsilon_{ns}\sim N(0,s_{ns}^2) \] \[(6)\] To set the student location, each new student is randomly assigned to a patch using a roulette wheel selection process where a patch’s probability of being chosen is proportional to its population data. Being \(pop_k\) the population data of a patch \(k\), and being \(K\) the set of patches, the probability of a patch \(k\) being selected as the student’s location will be given by Equation 7.
\[ P[k \; is \; selected]=\frac{pop_k}{\sum_{m \in K} pop_m} \] \[(7)\] The educational level reached by the student’s parents (EL) is measured in schooling years. New students’ EL depends on \(EL_{gl}\), a global variable indicating the new population’s average EL, whose value is set by using Equation 8. It depends on the time (\(t\)), and \({\beta_{el0}}\), \({\beta_{el1}}\), \({\beta_{el2}}\) parameters. The new \(EL_{gl}\), is then bounded to the range [0,22]. A student \(i\), located in patch \(k\), set their \(EL_i\) using Equation 9, where \(dEL_k\) is the deviation of patch \(k\)’s EL from the average EL, and a parameter \(s_{el}\) which indicates the standard deviation of the population’s EL. New students set their academic achievement, preference class, type (economically disadvantaged student or not), and budget constraint by following the same processes as the initial student population (see Appendix B, Initialization of Students Section).
\[ EL_{gl}=\beta_{el0}+\beta_{el1}(t+1)+\beta_{el2}{(t+1)}^2 \] \[(8)\] \[ EL_{i,k}=EL_{gl}+s_{el}\cdot dEL_{k} \] \[(9)\] Students switching schools and entering 1st grade level form their choice-set. To do so, following the model developed by Canals et al. (2022), they become aware of schools. First, students become aware of each school \(j\) with a school-specific probability \(p_j\). Second, they become aware of schools located at a distance \(T\) kms. or less from their home. Third, students become directly connected with other students from whom they will learn their previous school19. To which students a certain student will connect depend on their EL and is determined using a roulette wheel selection. The probability of a student \(l\) of being selected to be linked with student \(i\), will be given by Equation 10, where \(H\) is the set of students, \(\theta\leq0\) is a parameter and \(SD_{il}\) is the social distance between \(i\) and \(l\), measured as the absolute value of their EL difference.
\[ P[l \; being \; selected \; to \; be \; linked \; with \; i]=\frac{w_{i,l}}{\sum_{m\neq i \in H} w_{i,m}}, w_{i,l}=\frac{e^{\theta SD_{il}}}{1+e^{\theta SD_{il}}} \] \[(10)\] A student’s choice-set is then defined as all of the schools of which they are aware that offer the grade level they require and that they can afford20.
- Students calculate the propensity to choose each school of their choice-set, by following Equation 3.
Phase 4. Students apply to schools and schools select applicants
- Students apply to one school of their choice-set by following Equation 4.
- Schools select students from among their applicants. All students applying to non-selective schools are considered eligible. Students applying to selective schools are considered eligible only if they meet some academic requirements. This happens with a probability given by Equation 11, where \(p_{sel}\) is a parameter reflecting the probability of having applied to a selective school, P[\(R_i\)=1] is the student’s probability of being rejected by a school because of its academic requirements, \(A_i\) is the student academic achievement, \(Sec_i\) is a dummy variable with value 1 when the student is applying to secondary education and 0 otherwise, and \(\beta_{sel0}\), \(\beta_{sel1}\) and \(\beta_{sel2}\) are parameters. Non-eligible applicants are automatically rejected.
\[ \begin{split} \begin{gathered} P[R_i=0| i \; applied \; to \; a \; selective \; school] = 1 - \frac{P[R_i=1]} {p_{sel}}, \\ P[R_i=1]=\frac{e^{\beta_{sel0}+\beta_{sel1}A_i+\beta_{sel2}Sec_i}} {1+e^{\beta_{sel0}+\beta_{sel1}A_i+\beta_{sel2}Sec_i}} \end{gathered} \end{split} \] \[(11)\] Schools with enough seats available in a grade level accept all the eligible applicants. If a non-selective school does not have enough capacity for all the eligible applicants, it randomly selects until filling its capacity. If a selective school is in the same situation, it fills its vacancies by randomly choosing applicants based on their academic achievement. A roulette wheel selection process is used to select students. Being \(H_j\) the set of students applying to the selective school \(j\), the probability of a student \(i\) of being selected, is given by Equation 12.
\[ P[i \; is \; selected \; by \; j] = \frac{A_i+4} {\sum_{m \in H_j} A_m+4} \] \[(12)\] - Students who did not find a school discard the school that rejected them from their choice-set.
- Steps 1-3 are repeated until everyone is enrolled, or all the unenrolled students have empty choice sets. If there are still unenrolled students with empty choice-sets by the end of the process, they are allocated. If possible, they are assigned to the closest affordable non-selective school that has available capacity. Otherwise, they are assigned to the nearest non-selective public school that offers their required grade level.
Phase 5. Patches update their population data
To update the population data of patches, for a given area \(A\) (block or groups of blocks) identified in the input data, Equation 13 is applied, being \(pop_{A,t}\) the population data from the area \(A\) in time \(t\), \(\beta_{pop0}\), \(\beta_{pop1}\) and \(\beta_{pop2}\) parameters, and \(\epsilon_{pop}\) a random error. Then, for each patch \(k \in A\), Equation 14 is applied.
| \[ pop_{A,t}= \beta_{pop0}+\beta_{pop1}pop_{A,t-1}+\beta_{pop2}pop_{A,t-1}^2+\epsilon_{pop}, \epsilon_{pop}\sim N(0,s_{pop}^2)\] | \[(13)\] |
| \[ pop_k = \frac{pop_{A,t}} {\# patches \in A}\] | \[(14)\] |
Appendix B: Model Initialization Process
Model Initialization depends on a set of parameters and the schools’ and city areas’ GIS input datasets. The model sets school and patches initial characteristics using the input data, and then a student population is simulated.
Initialization of schools
To initialize the schools, the following initial attributes come directly from the GIS data: Geographic location, School Sector, Grade-span configuration, Value-added,21 Mean achievement of enrolled students,22 Monthly tuition, Selectivity, Year of opening, Year of school closing, Year of subscription to SEP program, Probability of being known through public information, and historical sequence of grade-span configuration. In addition, school \(j\)’s maximum capacity by grade is set based on its maximum capacity data \(MCD_j\), following Equation 15. Ceiling is a function that gives the smallest integer greater than or equal to its argument, and \(p_{sample}\) is a parameter representing the percentage of the student population of the city that is simulated. Only schools that were opened in the year 2004, the first simulated year, are represented in the model; the rest of them will appear later, based on their year of opening.
| \[ MC_{j} = max(1, ceiling(MCD_j, p_{sample}))\] | \[(15)\] |
Initialization of patches
Patches setup is based on the GIS data of a city, which includes three variables: an ID to identify the area, population data, and EL data. During the initialization, a given patch \(k\) that belongs to an area \(A\) will acquire a population value following Equation 14, with \(pop_{A,t}\) being the area’s population coming from the GIS data. It will also get a value in the variable \(dEL_k\) representing the distance between the patch’s EL and the average EL of the population, measured in standard deviations. The value will be given by Equation 16, where \(EL_A\) is the area’s SES coming from the GIS data, \(mEL_{pop}\) and \(sEL_{pop}\) are, respectively, the mean and standard deviation of the population’s EL, both of which are estimated using the area’s EL data, weighted by their population.
| \[ dEL_k = \frac{EL_A -mEL_{pop}} {sEL_{pop} }\] | \[(16)\] |
Initialization of students
After the schools and patches setup is done, an initial population of students is simulated. The model includes twelve parameters indicating the number of students that attended each grade in the city in 2004 (\(q_1,q_2,…,q_{12}\)), and each school \(j\) has data indicating which percentage of 2004 enrollees attended the school (\(pe_j\)). Being (\(GL_j\)) the set of grade levels offered by school \(j\), \(C\) the set of schools in the city, \(pe_{j,g}\) the percentage of a city’s students attending grade level \(g\) in school \(j\), Equation 17 is used to create \(ne_{j,g}\) students of grade \(g\) for each grade level that school \(j\) offers.
| \[ ne_{j,g} = max\left(1,p_{sample}q_g \frac {pe_{j,g}} {\sum_{l \in C} pe_{l,g}}\right), pe_{j,g}=\frac {pe_jq_g} {\sum_{l \in GL_j} q_l}\] | \[(17)\] |
New students acquire several variables. First, the EL of a new student attending school \(j\) would be randomly assigned following a normal distribution with mean \(EL_j\) and standard deviation \(sEL_{sch}\), being \(EL_j\) the educational level of the school’s students coming from the GIS data and \(sEL_{sch}\) a model parameter23. Second, each student is located in a patch a distance \(d\) from their school. The distance \(d\) is randomly set by a gamma distribution with parameters \(\alpha_{dist}\) and \(\lambda_{dist}\). Given a set of patches located at a distance \(d\) from school \(j\), the specific patch is selected using a roulette wheel selection process, with a probability of being chosen proportional to its population data. Being \(pop_k\) the population data of a patch \(k\), and being \(K\) the set of patches located at a distance \(d\) from school \(j\), the probability of a patch \(k\) of being selected as the student’s location will be given by Equation 18. If there is no patch with \(pop_k\)>0 at a given distance, a new distance is set, and the process is repeated until the student is located.
| \[ P[k \; being \; selected \; as \; student's \; location]=\frac{pop_k}{\sum_{m \in K} pop_m }\] | \[(18)\] |
Third, new students acquire the following other initial characteristics based on their EL.
- Students’ academic achievement is simulated as a random variable with a given correlation \(\rho\) with students’ EL.
- Each student \(i\) gets one of two possible preference classes, with a probability of belonging to class 1 given by Equation 19, where \(\alpha_{class}\) and \(\beta_{class}\) are parameters.
\[ P[class_i=1]=\frac{e^{\alpha_{class}+\beta_{class}EL_i}} {1+e^{\alpha_{class}+\beta_{class}EL_i}} \] \[(19)\] - Students may randomly become economically disadvantaged, with a probability given by Equation 20 and \(\beta_p\) are parameters.
\[ P[disadv_i=1]=\frac{e^{\alpha_p+\beta_pEL_i}}{1+e^{\alpha_p+\beta_pEL_i}} \] \[(20)\] - Students are randomly assigned a budget constraint. The maximum monthly tuition that they can afford will be given by Equation 21, where \(\beta_{bc0}\), \(\beta_{bc1}\) and \(\beta_{bc2}\) are parameters and \(\epsilon_{bc}\) is a random error.
\[ BC_i=max(0,\beta_{bc0}+\beta_{bc1}EL_i+\beta_{bc2}disadv_i+\epsilon_{bc}),\epsilon_{bc} \sim N(0,s_{bc}^2) \] \[(21)\]
Simulation of the initial state
Then, to simulate an initial state that is the result of the model itself, we followed the following processes:
- Updating agents’ characteristics: We run twelve model iterations, with only two differences from a regular iteration: (i) The number of new students created in each iteration is \(p_{sample}q_g\), with \(q=12\) in the first iteration, \(q=11\) in the second one, and so on, until being \(q=1\). (ii) Every student passes their grade level. These two modifications allow us to keep the number of students by grade stable. After the twelve iterations, the whole population was generated by the model’s rules.
- We repeated step 1 five more times, recording the mean squared error, which is measured as the mean squared difference in the schools’ percentage of enrollment before and after each application of step 1. We also recorded the moving average of the three last mean squared errors.
- If the moving average of the mean squared error is \(\leq1\%\), the process stops. Otherwise, step 1 is repeated until the moving average of the mean squared error \(\leq1\%\). If step 1 is repeated 50 times, and the moving average of the mean squared error is still >\(1\%\), the simulation stops reporting that the setup process failed.
Appendix C: Calibration and Estimation of Model Parameters
In this appendix, we describe the estimation and calibration of model parameters. Tables 3 and 4, at the end of this Appendix, show a summary of these processes and the calibrated parameters for each city, respectively. Unless mentioned otherwise, calibration and estimation processes were made separately for each city.
Student’s achievement progression
Parameters from Equation 1, which models the students’ achievement and schools’ value-added, were estimated using data from students who took SIMCE tests both in 4th grade and 8th grade or both in 8th grade and 10th grade since 200224. Students’ Math and Language SIMCE test scores were standardized by year, and then averaged by student. Given that the SIMCE test is not taken in every grade level, we cannot directly estimate the parameters of Equation 1. Thus, we made yearly estimations of the hierarchical linear models given by Equations 22 and 23, where \(A_{i,g}\) is the achievement of student \(i\) in grade \(g\), \(u_{j,g}\) is school \(j\)’s random effects for grade \(g\), \(a_g\),\(b_g\) and \(s_g\) are parameters and \(e_g\) an error term that depends on the grade \(g\).
| \[ A_{i,10}= a_{10}+b_{10}A_{i,8}+u_{j,10}+e_{10}, e_{10} \sim N(0,s_{10}^2)\] | \[(22)\] |
| \[ A_{i,8}= a_{8}+b_{8}A_{i,4}+u_{j,8}+e_{8}, e_{8} \sim N(0,s_{8}^2)\] | \[(23)\] |
To get the parameters of Equation 1, we looked for an equivalence between it and Equations 22 and 23. For the case of 10th grade, Equation 1 implies that:
| \[\begin{aligned} A_{i,10} = & \alpha_{ach}+\beta_{ach}A_{i,9}+VA_j+\epsilon_{ach} \\ A_{i,10} = & (\alpha_{ach}+VA_j+\epsilon_{ach})(1+\beta_{ach})+\beta_{ach}^2A_{i,8} \end{aligned}\] | \[(24)\] |
Therefore, making an equivalence between Equation 1 and 24, we can establish that:
| \[ \begin{aligned} a_{10} = & \alpha_{ach} (1 +\beta_{ach}) \\ b_{10} = & \beta_{ach}^2 \\ u_{j,10} = & VA_j (1+\beta_{ach}) \\ e_{10} = & \epsilon_{ach}(1 +\beta_{ach}) \\ s_{10}^2 = & s_{ach}^2(1 +\beta_{ach}^2) \end{aligned}\] | \[(25)\] |
A similar procedure for the case of 8th grade allows us to establish that:
| \[ \begin{aligned} A_{i,8} = & (\alpha_{ach}+VA_j+\epsilon_{ach})(1+\beta_{ach}+\beta_{ach}^2+\beta_{ach}^3)+\beta_{ach}^4A_{i,4} \\ a_{8} = & \alpha_{ach} (1 +\beta_{ach}+\beta_{ach}^2+\beta_{ach}^3) \\ b_{8} = & \beta_{ach}^4 \\ u_{j,8} = & VA_j (1+\beta_{ach}+\beta_{ach}^2+\beta_{ach}^3) \\ e_{8} = & \epsilon_{ach}(1 +\beta_{ach}+\beta_{ach}^2+\beta_{ach}^3) \\ s_{8}^2 = & s_{ach}^2(1 +\beta_{ach}^2+\beta_{ach}^4+\beta_{ach}^6) \end{aligned}\] | \[(26)\] |
Using the yearly estimations of Equation 22, we used Equation 25 to estimate parameters \(\alpha_{ach}\), \(\beta_{ach}\) and \(s_{ach}^2\), and the value-added \(VA_{j}\) for each year, and averaged those estimations to have a 10th grade mean value. We followed the same process for 8th grade (using the estimation of Equation 23, and Equation 26). Finally, we averaged the mean values for 8th and 10th grades, obtaining the final parameters and school’s value-added.
Student’s probability of being retained and dropout
To estimate the probability of being retained (\(r\)), we calculated the yearly relative frequency of students who failed their grade level using students’ achievement and enrollment administrative datasets for the years 2004-2017. Then, we averaged those values into a single value. To estimate parameters of Equation 5, we used the same datasets to calculate the yearly relative frequency of dropping out for students who passed and those who failed their grade level. For the case of students who passed, we averaged those values to set the \(\alpha_{pass}\) parameter. For the ones who failed, as there was wide variation across grade levels, we fitted an exponential function (using OLS) to the data of dropout rate by grade level, estimating \(\alpha_{fail}\) and \(\beta_{fail}\), Equation 5’s parameters.
School’s tuition progression
To estimate the parameters of Equation 2, we used schools’ tuition data for the period 2004-2017. In most cities, there were no public schools charging tuition, and therefore, all parameters (\(\alpha_{Ts}, \beta_{Ts}\) and \(\epsilon_{Ts}\)) were set to zero. In the cities and sectors where some schools charge tuition, considering only the schools that charged tuition during the period, for each sector, we estimated a Model AR(1) through OLS to predict schools’ fees. In all cases, the variances of the error term \(s_{Ts}^2\) are assumed to be equal to ones of the residuals.
Probability of switching schools for students not forced to
Parameter \(sp_{s,rs}\) indicates the probability of switching school for students who are not forced to, depending on the sector of their school \(s\), and whether they failed, passed 8th grade level, or passed another grade. The parameter values were calculated using students’ enrollment and achievement administrative data for the period 2004-2017. Specifically, they were measured as the average of the yearly relative frequency of switching of each student set.
Progression of number of students entering the first grade level
Parameters of Equation 6 were estimated through OLS and using students’ enrollment data for the period 2004-2017. The variance of the error term \(s_{ns}^2\) is assumed to be equal to the one of the residuals. \(p_{sample}\) parameter is set in the minimum percentage, such that the initial simulated population was at least =Min(600, 30 \(\cdot\) number of schools). This is a sample size large enough to have a considerable number of students by school and small enough to prevent excessive computation time.
Student’s process of becoming aware of schools
The parameters related to the process of becoming aware of school options (the distance threshold \(T\), the number of connections \(n\), and the homophily parameter \(\theta\) were calibrated by following the approach of Canals et al. (2022). We used their model of awareness set formation allowing the students to become aware of schools through three mechanisms (Geographic Proximity, Public Information, and Social Interactions). The model was initialized with actual student data coming from Survey of School Choice 2016, and then, a genetic algorithm was used to calibrate the parameters. The aim was to choose parameter values that minimized the difference between the choice sets simulated by the model and the actual choice-sets reported in the survey. To do so, we used the loss function and search parameters proposed by the authors.
Progression of population’s EL
Using data from students who took the SIMCE test in 4th, 8th, 10th grades during 2002-2018, we obtained the average parents’ schooling years of students. Using said data, we estimated Equation 8 through OLS. In addition, we calculated the standard deviation of parents’ schooling years by year, and we set the parameter \(s_{el}\) (of Equation 9) as their mean value.
Student’s probability of belonging to class 1 and propensity to choose a school
Parameters from Equation 19, which governs the students’ preference class, and Equation 3, which determines the propensity to choose a school, were jointly estimated through maximum likelihood using a Latent Class Logit Model, and assuming two classes of agents25. We used data from the Survey of School Choice 2016, which has data about families’ actual choice-set, their most preferred school, their location, and parents’ schooling years. The mean achievement of the school’s students was measured as the average of Math and Language SIMCE test, previously standardized.
Student’s probability of meeting the requirements of a selective school
To estimate the parameters of Equation 11, we used data from the survey for the parents of students who took the SIMCE test, where they were asked about why they chose their children’s schools. They were allowed to select as many options as they wanted, including "because they were rejected by another school"26. Then, we used maximum likelihood to estimate a logit model to predict the probability of having been rejected by a school. Student achievement \(A_i\) was measured by the average of Math and Language SIMCE test, previously standardized by year. The additional parameter \(p_{sel}\) was estimated as the relative frequency of parents’ choosing as a first option a selective school in the Survey of School Choice 2016.
Area’s progression of population data
Parameters of Equation 13 were estimated through OLS, relying on data from 1992, 2002, and 2012 Chilean Population and Housing Census. For Osorno and Punta Arena we used data from areas that correspond to groups of blocks. For the case of Vallenar and Salamanca, the smallest cities, as there are too few areas in the whole city, we used block data.
Initial number of students by grade level
The parameters \(q_1,q_2,\dots,q_{12}\) used in Equation 17, which indicate the initial number of students by grade level, were directly calculated from the students’ enrollment dataset of 2004.
Initial standard deviation of the EL of students attending a school
We used SIMCE data from 4th, 8th and 10th grade students of the years 2005, 2004 and 2003, respectively. We measured a student’s EL as the average schooling years of their parents. To estimate the parameter \(sEL_{sch}\), first, we estimated the standard deviation of the students’ EL by school, grade, and year. Then, we averaged the estimated standard deviations.
Student’s initial distance to school
To obtain the two parameters of the gamma distribution that defined the distance between the student’s home and school in the model initialization (\(\alpha_{dist}\) and \(\lambda_{dist}\)), we fitted a gamma distribution, through maximum likelihood, to the distribution of the students’ distance to their school. To do so, we used data from the Survey of School Choice 2016 of households whose children were currently attending the school system.
Correlation between initial students’ academic achievement and EL
To get parameter \(\rho\), we estimated the correlation between the 4th-grade standardized test scores and the parents’ schooling years by year (See note 24 for data details). Then, we set \(\rho\) as the average value.
Student’s probability of being an economically disadvantaged student
Parameters from Equation 20 that model the probability of being an economically disadvantaged student were estimated through a logit model, using maximum likelihood. To do so, we used administrative data about economically disadvantaged students (priority students) and data from students who took the SIMCE test in 4th grade, 8th grade, and 10th grade between 2012 and 201627. SIMCE datasets include the parents’ schooling years; we used the average schooling years of the parents to measure a student’s EL.
Student’s budget constraint
To calibrate the parameters of Equation 21, which sets the students’ budget constraint, we used data from Survey of School Choice 2016, which included the three most preferred schools from each household, combined with 2016 administrative data about priority students, restricting the sample to surveyed households whose children were already in the school system. Survey data was weighted to match some characteristics of the actual population of the cities because it was a non-self-weighting sample. We conducted a single calibration process using all the surveyed households’ data instead of making a calibration process separately for each city. Therefore, every city will have the same parameter values for this equation28.
Parameters of Equation 21, were calibrated by minimizing a loss function through a genetic algorithm (GA) implemented in RStudio 1.1.463. For calibration purposes, we define a household’s “observed budget constraint” as the maximum monthly tuition among the three most preferred schools reported in the survey, measured in 2017 CLP (1,000 CLP 2017 = 1.6 USD of the same year)29. The process of calibrating the parameters was based on simulating an observed budget constraint with candidate parameters and comparing them with the observed budget constraint from the survey data. Given a set of candidate parameters, we simulate the observed budget constraint following two steps. First, we predict students’ budget constraint using Equation 21, the data, and the candidate parameters. Second, considering only the schools located in a household’s city, we set their simulated observed budget constraint at the schools’ maximum monthly tuition that they can afford with their predicted budget constraint.
The quality of the candidate solution was measured by a loss function given by Equation 27 and with a [-1,0] range; -1 indicates a perfect match between simulated and survey data, and zero the opposite. \(BC_0, p_0\) and \(p_e\) are the observed budget constraint, the percent of households whose observed budget constraint is zero, and the percent of households whose observed budget constraint is larger than 110,000 CLP in the survey data, while \(BC_{0, simul}, p_{0, simul}\) and \(p_{e, simul}\) are the same estimated with the simulated data. Table 2 shows the parameters used in the GA with the aim of finding the set of parameters minimizing the Loss Function.
| \[ LF = \frac {-corr(BC_{0, simul},BC_0)+(abs(p_{0, simul}-p_0)-1)+(abs(p_{e, simul}-p_e)-1)} {3}\] | \[(27)\] |
| Search algorithm’s parameters | |
|---|---|
| Parameter name | Parameter name |
| Mutation rate | 20% |
| Mutation fraction (mf)* | 20% |
| Population size | 1000 |
| Selection criteria | Tournament selection |
| Number of tournaments | 50 |
| Stop-Criteria | 1000 iterations |
| Population model | Constant population size. |
| New population corresponds to the top candidate solutions considering both the previous generation and their offspring. | |
| Range of parameters of a candidate solution** | |
| Parameter | Range |
| \(\beta_{bc0}\) | [-100,100] |
| \(\beta_{bc1}\) | [0,100] |
| \(\beta_{bc2}\) | [-100,0] |
| \(s_{bc}\) | [5,50] |
| Process | Calibration process | Data source |
|---|---|---|
| Student’s achievement progression | Hierarchical linear model (Maximum likelihood) | Students’ SIMCE Scores 2002-20181 |
| Student’s Probability of Being Retained | Annual average of the relative frequency of student passing their grade level. | Student achievement, and Student enrollment 2004-20172 |
| Student’s Probability of Dropout | For students who passed their grade level: annual average of the relative frequency of dropout. | Student achievement, and Student enrollment 2004-20172 |
| For students who failed their grade level: Exponential regression (OLS) | ||
| School’s tuition progression | Autoregressive model (OLS) | Shared Funding 2004-20172 |
| Probability of switching schools for students not forced to | Annual average relative frequency of students switching schools | Student achievement, and Student enrollment 2004-20172 |
| Progression of number of students entering the first grade level | Quadratic regression (OLS) | Student enrollment dataset 2004-20172 |
| Student’s process of becoming aware of schools | Genetic Algorithm (Canals et al. 2022) | Survey of School Choice 20162 |
| Progression of population’s EL | For standard deviation of students’ EL: Annual average of standard deviation of parents’ schooling years. | Survey for parents and guardians (SIMCE) 2002-20181 |
| For average EL of the new population: Quadratic regression (OLS) | ||
| Student’s probability of belonging to preference class 1 and Propensity to choose a school | Latent class logit model (Maximum likelihood) | Survey of School Choice 20162 |
| Student’s probability of meeting the requirements of a selective school, conditional to having applied to said school | For probability of applying to a selective school: Relative frequency of parents choosing a selective school as the first option. | Survey of School Choice 20162, Survey for parents and guardians (SIMCE) 2009-20121 and Students’ SIMCE Scores 2009-20121 |
| For probability of not meeting a selective school's academic requirements: Logit model (Maximum likelihood) | ||
| Area’s progression of population data | Quadratic regression (OLS) | Chilean Population and Housing Census 1992, 2002 and 20123 |
| Initial number of students by grade level | Count of enrollees | Student enrollment 20042 |
| Initial Standard deviation of the EL of students attending a school | Average standard deviation of the EL of students | Survey for parents and guardians (SIMCE) 2003-20051 |
| Student’s initial distance to school | Fitting gamma distribution (Maximum Likelihood) | Survey of School Choice 20162 |
| Correlation between initial students’ academic achievement and EL | Correlation | Survey for parents and guardians (SIMCE) 2002-2013 and Students’ SIMCE Scores 2002-20131 |
| Student’s probability of being an economically disadvantaged student | Logit model (Maximum likelihood) | Survey for parents and guardians (SIMCE) 2012-20161 and Priority and SEP Beneficiary Students 2012-20162 |
| Student’s budget constraint | Genetic Algorithm | Survey of School Choice, and Priority and SEP Beneficiary Students 20162 |
| Process | Parameter | Osorno | Punta Arenas | Vallenar | Salamanca | |
|---|---|---|---|---|---|---|
| Student’s achievement progression (Equation 1) | \(\alpha_{ach}\) | 0.003 | -0.034 | -0.073 | -0.029 | |
| \(\beta_{ach}\) | 0.832 | 0.837 | 0.82 | 0.87 | ||
| \(s_{ach}\) | 0.365 | 0.368 | 0.361 | 0.338 | ||
| Student’s probability of being retained | \(r\) | 0.0688 | 0.0371 | 0.0379 | 0.0507 | |
| Student’s probability of dropout (Equation 5) | \(\alpha_{pass}\) | 0.015 | 0.011 | 0.008 | 0.009 | |
| \(\alpha_{fail}\) | 0.01 | 0.008 | 0.012 | 0.017 | ||
| \(\beta_{fail}\) | 0.247 | 0.305 | 0.29 | 0.233 | ||
| School’s tuition progression (Equation 2)1 | \(\alpha_{Tp}\) | 0.4 | 0 | 0 | 0 | |
| \(\beta_{Tp}\) | 0.583 | 0 | 0 | 0 | ||
| \(s_{Tp}\) | 1.09 | 0 | 0 | 0 | ||
| \(\alpha_{Tv}\) | 1.55 | 7.785 | 0.559 | 0 | ||
| \(\beta_{Tv}\) | 0.915 | 0.851 | 0.985 | 0 | ||
| \(s_{Tv}\) | 7.722 | 10.308 | 2.216 | 0 | ||
| \(\alpha_{Tf}\) | 63.31 | 34.85 | 32.746 | 0 | ||
| \(\beta_{Tf}\) | 0.4758 | 0.69 | 0.728 | 0 | ||
| \(s_{Tf}\) | 5.575 | 14.427 | 5.252 | 0 | ||
| Probability of switching schools for students not forced to1,2 | \(sp_{p,r}\) | 0.308 | 0.258 | 0.227 | 0.294 | |
| \(sp_{p,p8}\) | 0.023 | 0.186 | 0.031 | 0.139 | ||
| \(sp_{p,po}\) | 0.067 | 0.084 | 0.071 | 0.078 | ||
| \(sp_{v,r}\) | 0.365 | 0.444 | 0.257 | 0.352 | ||
| \(sp_{v,p8}\) | 0.187 | 0.183 | 0.06 | 0.288 | ||
| \(sp_{v,po}\) | 0.097 | 0.073 | 0.036 | 0.073 | ||
| \(sp_{f,r}\) | 0.316 | 0.388 | 0.514 | 0 | ||
| \(sp_{f,p8}\) | 0.061 | 0.121 | 0.066 | 0 | ||
| \(sp_{f,po}\) | 0.047 | 0.085 | 0.058 | 0 | ||
| Progression of number of students entering the first grade level (Equation 6) | \(p_{sample}\) | 0.074 | 0.052 | 0.058 | 0.2 | |
| \(\beta_{ns0}\) | 11864093.27 | 5835721.74 | 4479041.63 | 373858.47 | ||
| \(\beta_{ns1}\) | -11798.888 | -5794.583 | -4456.103 | -376.384 | ||
| \(\beta_{ns2}\) | 2.934 | 1.4389 | 1.109 | 0.095 | ||
| \(s_{ns}\) | 65.03 | 36.38 | 26.87 | 16.6 | ||
| Student’s process of becoming aware of schools | \(T\) | 0.7 | 0.97 | 0.43 | 0.51 | |
| \(n\) | 8 | 7 | 13 | 19 | ||
| \(\theta\) | -1.85 | -2.1 | -1.49 | -1.39 | ||
| Progression of population’s EL (Equations 8 and 9) | \(s_{el}\) | 3.61 | 3.14 | 3.22 | 3.04 | |
| \(\beta_{el0}\) | -43711.75 | -74273.78 | -45760.04 | -34234.15 | ||
| \(\beta_{el1}\) | 43.409 | 73.9 | 45.493 | 33.965 | ||
| \(\beta_{el2}\) | -0.011 | -0.018 | -0.011 | -0.008 | ||
| Student’s probability of belonging to preference class 1 and Propensity to choose a school (Equations 3 and 19) | \(\alpha\) | 0.173 | -3.055 | 0.803 | 2.203 | |
| \(\beta\) | 0.085 | 0.205 | -0.084 | -0.124 | ||
| \(\beta_{11}\) | 0.455 | -1.883 | -0.925 | 0.046 | ||
| \(\beta_{21}\) | -5.099 | 0.412 | 0.55 | 31.022 | ||
| \(\beta_{12}\) | -0.214 | 1.135 | -0.165 | -0.566 | ||
| \(\beta_{22}\) | 3.923 | -0.344 | 1.497 | 165.05 | ||
| \(\beta_{3}\) | 1.45 | 1.311 | 1.255 | 1.418 | ||
| \(\beta_{4}\) | 0.604 | 0.216 | 0.146 | -1.8 | ||
| \(\beta_{5}\) | 1.769 | 1.848 | 0.75 | 1.926 | ||
| \(\beta_{6}\) | -0.259 | -0.175 | -0.214 | -0.186 | ||
| Student’s probability of meeting the requirements of a selective school, conditional to having applied to said school (Equation 11) | \(p_{sel}\) | 0.902 | 0.852 | 0.764 | 0.464 | |
| \(\beta_{sel0}\) | -4.111 | -3.985 | -4.061 | -4.631 | ||
| \(\beta_{sel1}\) | -0.537 | -0.468 | -0.334 | -0.521 | ||
| \(\beta_{sel2}\) | 1.04 | 0.627 | 0.438 | 0.257 | ||
| Area’s progression of population data (Equation 13) | \(\beta_{pop0}\) | 177.91 | 143.347 | 2.312 | 2.957 | |
| \(\beta_{pop1}\) | 0.865 | 0.9 | 0.918 | 0.936 | ||
| \(\beta_{pop2}\) | 0.00003 | 0.00002 | 0.0008 | 0.0004 | ||
| \(s_{pop}\) | 105.737 | 81.644 | 5.646 | 7.092 | ||
| Initial number of students by grade level | \(q_1\) | 2408 | 1905 | 828 | 200 | |
| \(q_2\) | 2333 | 1981 | 913 | 231 | ||
| \(q_3\) | 2412 | 1885 | 929 | 213 | ||
| \(q_4\) | 2451 | 1939 | 863 | 238 | ||
| \(q_5\) | 2535 | 1960 | 917 | 233 | ||
| \(q_6\) | 2544 | 2069 | 970 | 223 | ||
| \(q_7\) | 2613 | 2130 | 1058 | 261 | ||
| \(q_8\) | 2558 | 2026 | 1025 | 239 | ||
| \(q_9\) | 3457 | 2331 | 1159 | 379 | ||
| \(q_{10}\) | 3080 | 2199 | 1035 | 317 | ||
| \(q_{11}\) | 2615 | 1885 | 997 | 283 | ||
| \(q_{12}\) | 2056 | 1715 | 872 | 249 | ||
| Initial Standard deviation of the EL of students attending a school | \(sEL_{sch}\) | 2.68 | 2.57 | 2.5 | 2.64 | |
| Student’s initial distance to school | \(\alpha_{dist}\) | 1.527 | 1.846 | 2.088 | 2.295 | |
| \(\lambda_{dist}\) | 1.427 | 0.975 | 0.618 | 0.342 | ||
| Correlation between initial students’ academic achievement and EL | \(\rho\) | 0.328 | 0.328 | 0.336 | 0.265 | |
| Student’s probability of being an economically disadvantaged student (Equation 20) | \(\alpha_p\) | 2.917 | 2.204 | 3.745 | 2.17 | |
| \(\beta_p\) | -0.252 | -0.278 | -0.295 | -0.205 | ||
| Student’s budget constraint (Equation 21) | \(\beta_{bc0}\) |
-146.013 | ||||
| \(\beta_{bc1}\) | 18.921 | |||||
| \(\beta_{bc2}\) | -42.168 | |||||
| \(s_{bc}\) | 16.654 | |||||
Appendix D: Model Validation
Figure 4 in the main text shows the real and the simulated trends for the city of Punta Arenas using the calibrated model in the baseline scenario. The following pictures display the corresponding results for the other cities.
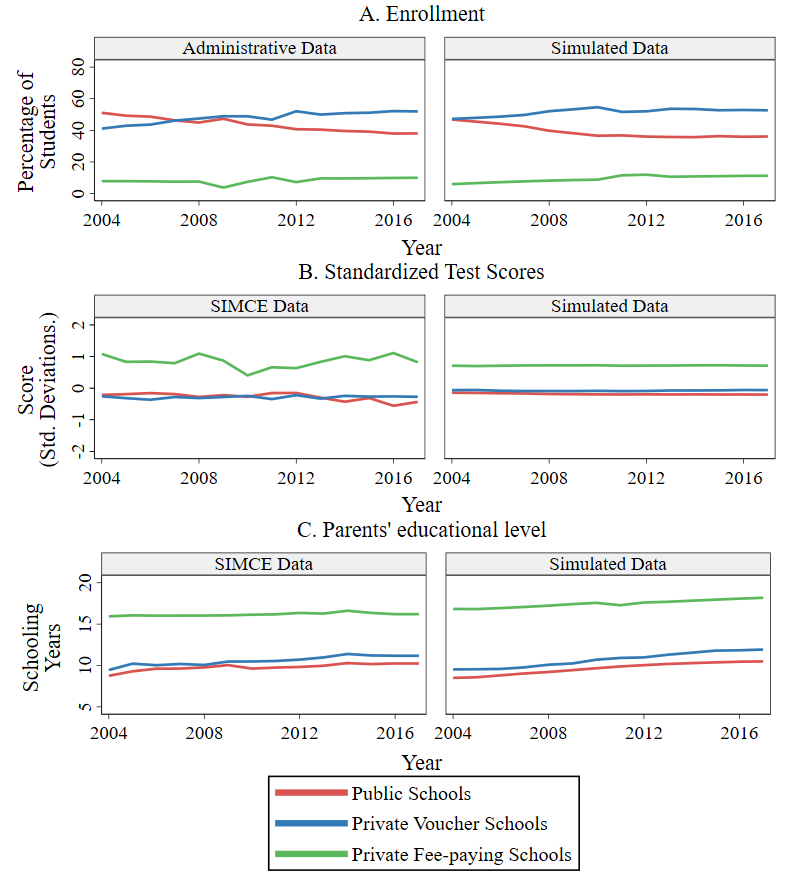
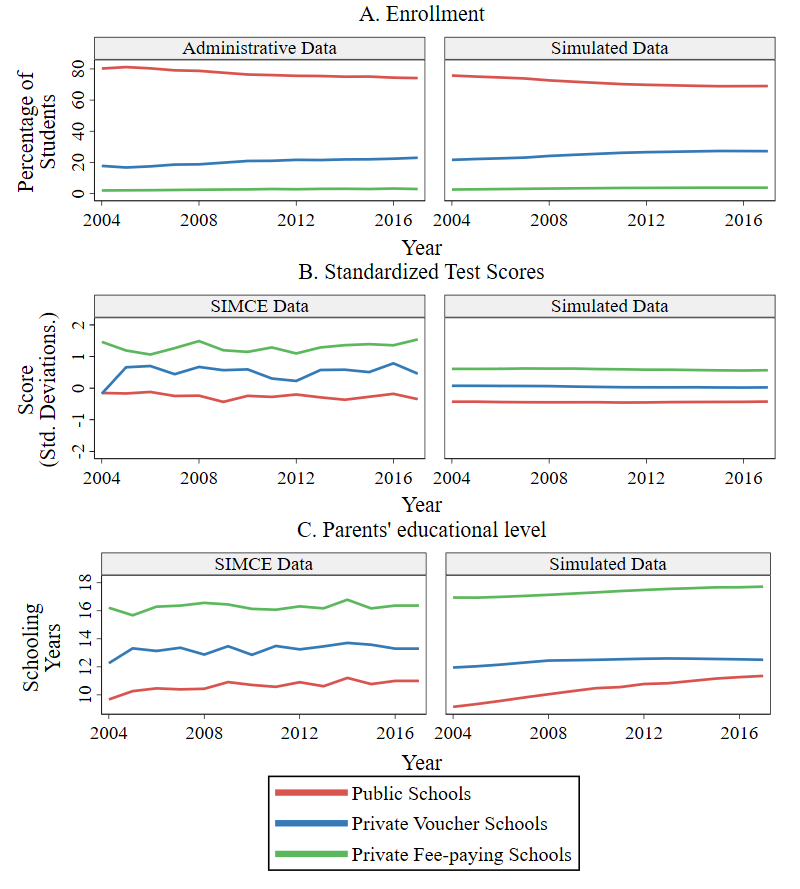
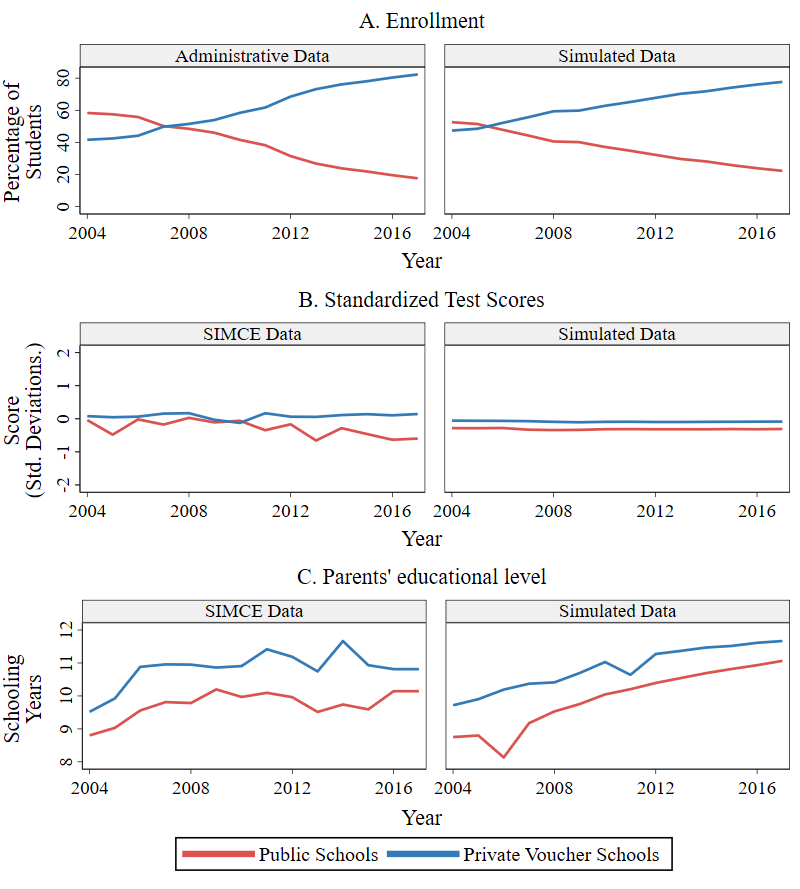
Appendix E: Simulation Experiments’ Details
Experiments 3, 4, 5, 6 and 7 were described in detail in the main text; however, the remaining experiments need further explanation.
Experiment 1: Stable number of schools by sector
The number of schools by sector remains stable since 2004. To do so, schools neither close nor change their sector over time, and no new schools are created.
Experiment 2: Public sector reacts to the demand
In every iteration, a new public school is opened. To avoid affecting other characteristics of the public sector, the new school is a copy of a random public school but located in a new place30. To define the new location, we use the concept of a patch’s neighborhood, defined as the area located at a distance\(\leq 1.5T\) from the patch. If there are patches without a single school in their neighborhood, the new school will be located in the patch of that set that has the highest number of students. If every patch has at least one school in its neighborhood, the new school will be located in the patch with the highest ratio between the number of students and the number of schools in its neighborhood. In either case, if multiple patches have the highest value, one of them will be randomly selected.
Experiment 8: Coordination of public schools to offer primary and secondary education
In experiment 8, public schools can create partnerships between them. In every iteration, if any primary public school does not have a partner secondary school, it will search for one. To do so, it will identify the set of public secondary schools with a compatible grade-span configuration that could absorb its enrollment. Schools offering 1°-4° grade levels will have no compatible schools as no public schools offer 5°-12° grade levels; thus, they will be excluded from creating partnerships. Public schools offering 1°-6° and 1°-8° grade levels will be considered compatible with schools offering 7°-12° and 9°-12° grade levels, respectively. A compatible secondary school can absorb a primary school \(j\)’s enrollment if its vacancies by grade level, minus the sum of its current partner schools’ vacancies is larger or equal to \(j\)’s vacancies by grade level. From the compatible public schools that can absorb a primary school’s enrollment, it will choose the closest one to create a partnership. Once a partnership is created, none of the involved schools will change their grade-span configuration over time.
The creation of a partnership will have two implications. First, in each iteration, once a student passes the last grade level offered by a primary school that has a partnership with a school that offers secondary education, they will immediately enroll for the next grade level at the primary school’s partner school. Independent of this, the student may decide to switch to another school based on the standard switching school rule. Second, when families determine their propensity to choose the schools from their choice-set (Equation 3), they will consider that primary schools with partnerships allow them to ensure a seat both in primary and secondary education.
Experiment 9: Stable socioeconomic status of the population
The average population’s EL and the geographic distribution of the population remain the same. To do so, the population’s average EL global variable \(EL_{gl}\), is never updated. In addition, patches do not update their population data. This was necessary because student’s EL depends both on \(EL_{gl}\) and the patch’s EL. Therefore, even if \(EL_{gl}\) is stable, if the population data from the patches is updated, the number of students coming from each patch would vary. Consequently, an increase in the population of low EL patches would lower the aggregate EL level, while an increase in the population of high EL patches would raise the aggregate EL level.
Appendix F: Experiments’ Impact on Private Enrollment
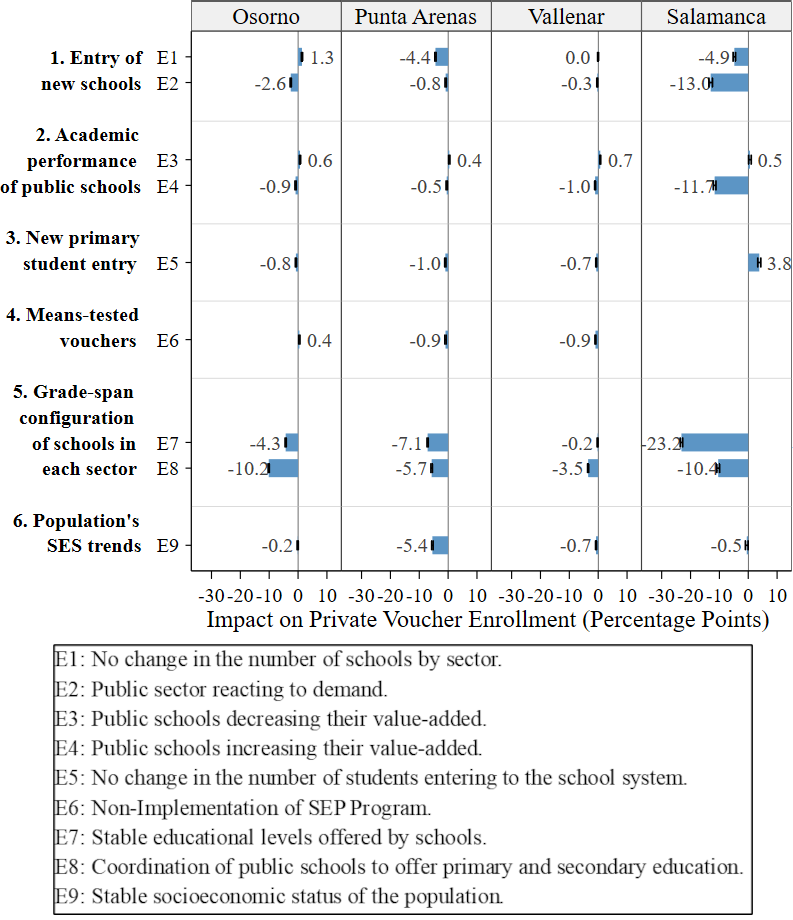
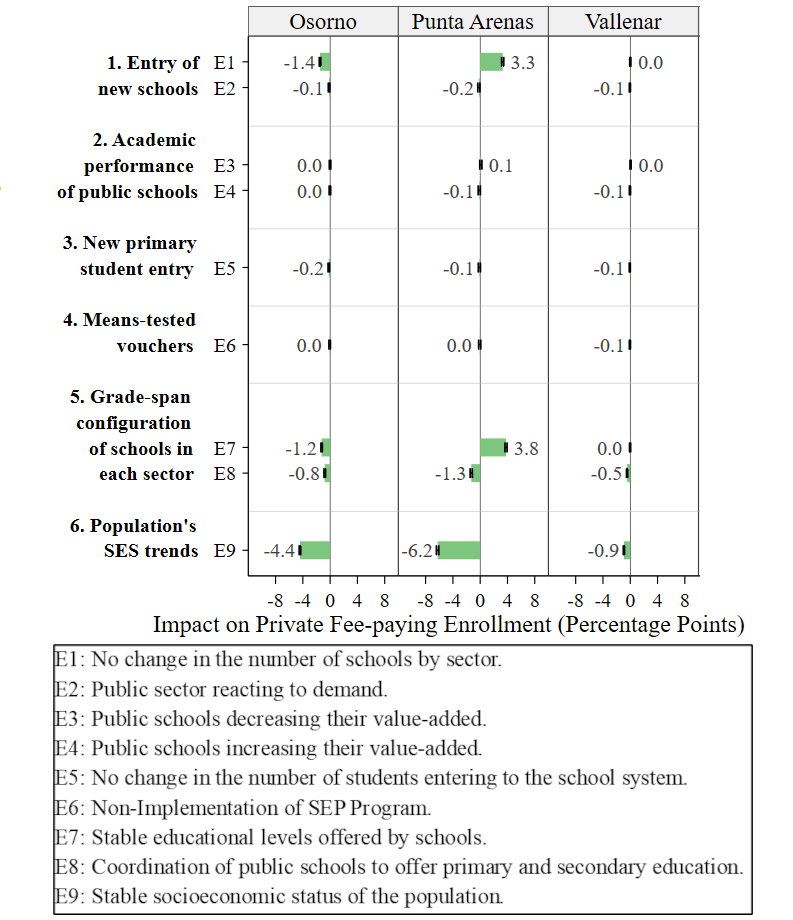
Appendix G: Experiments’ Enrollment Difference by Sector
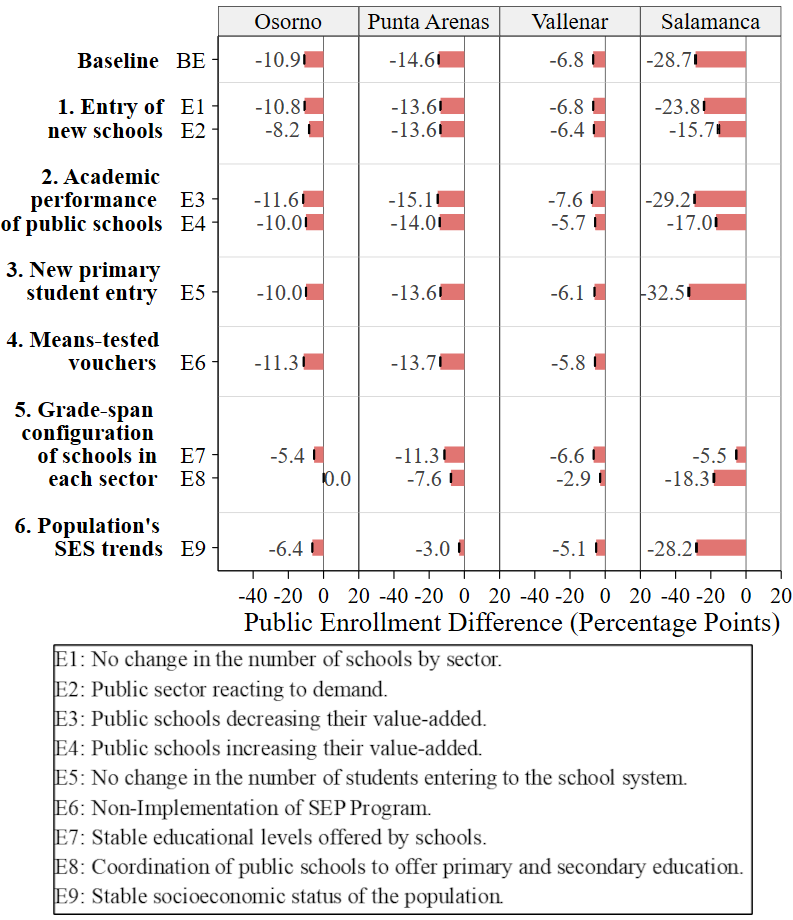
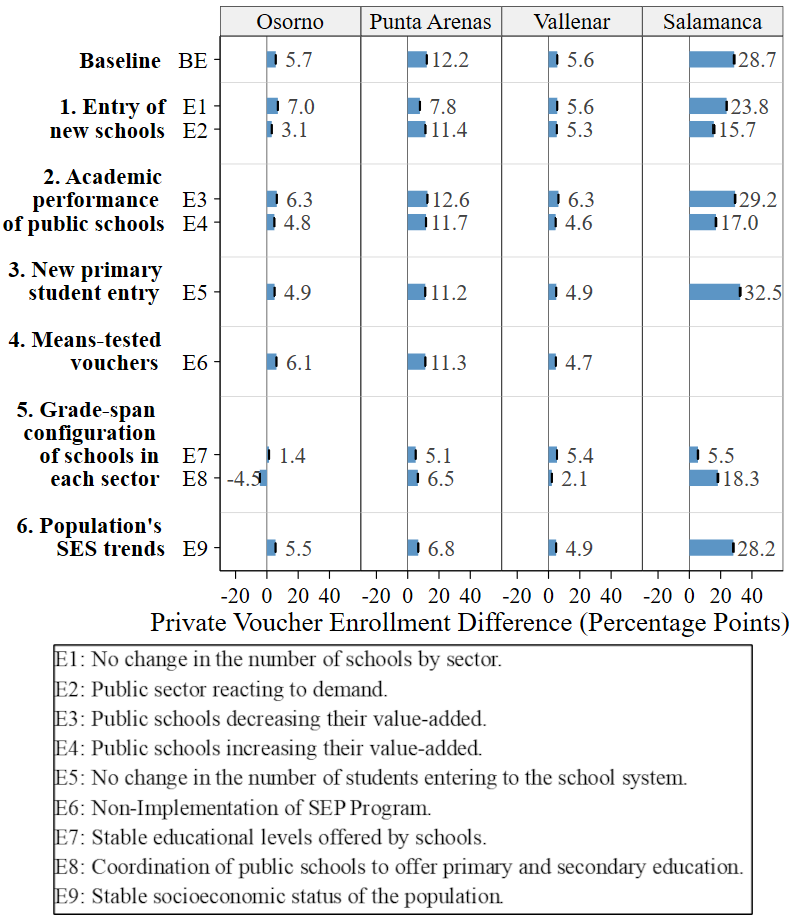

Appendix H: Experiments’ Public Enrollment Over Time
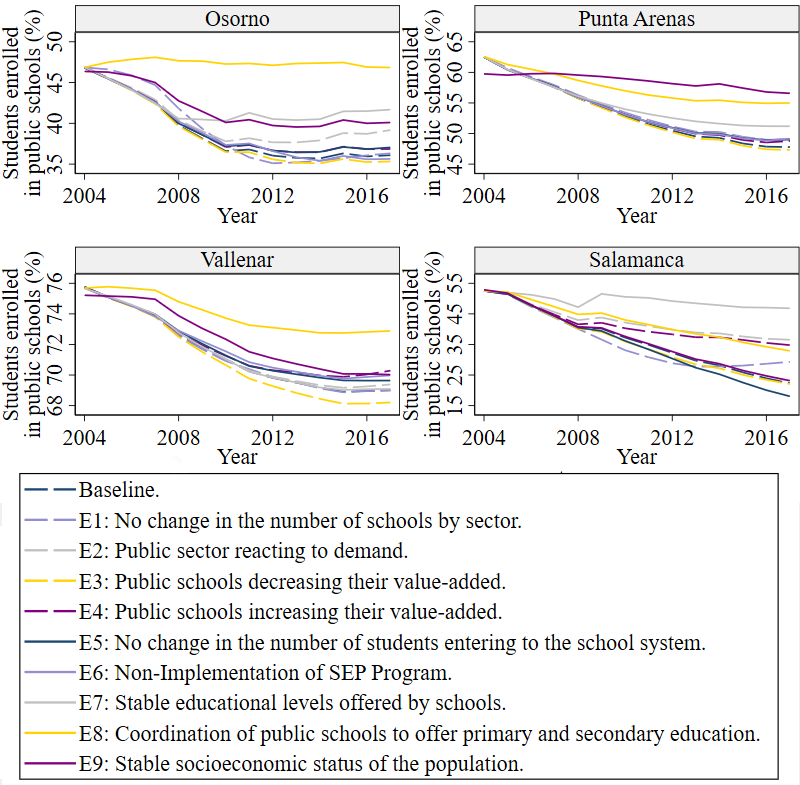
Notes
- Selective schools usually consider students’ previous transcripts and/or require entrance tests to assess students’ achievements.↩︎
- Since 1988, private voucher schools were allowed to charge tuition, but the 1993 reform increased the maximum tuition allowed. The law establishes that when private voucher schools charge tuition, they receive a lower voucher amount; with the 1993 reform, this reduction was diminished, weakening the incentives to offer free education. This law also allowed secondary public schools to charge tuition in cases where they had the approval of the parents, but very few schools did so.↩︎
- Authors calculations based on data provided by Ministry of Education and Agencia de Calidad de la Educación.↩︎
- The model can be easily adapted to simulate the enrollment trends for a longer period, but in this case, we used it to study the school enrollment in Chile for the period 2004 to 2016.↩︎
- The NetLogo code for the model can be accessed via the CoMSES Computational Model Library: https://www.comses.net/codebases/a03bcb4e-733c-41d0-b3ec-e4035b06faf4/releases/1.0.0/↩︎
- The options of grade-span configurations were defined based on the empirical configurations.↩︎
- Students looking for a school for the first time will connect to \(n\) students. Students who have looked for a school before will have \(x\leq n\) number of connections because some old connected students might have disappeared from the model; thus, they will create \(n-x\) new links.↩︎
- \(SD_{ij}=abs(EL_j-EL_i)\), where \(EL_{j}\) is the average EL of the parents of the students that attended school \(j\) the last academic year and \(EL_{i}\) is the educational level of the student’s parents.↩︎
- An alternative and appealing way of operationalizing peer effects is to consider the proportion of connected students attending to a given option (e.g., Leoni (2022) and Manzo (2013)). Unfortunately, we did not have the data needed to calibrate the model using this measure (we only identified if a student knew someone in the school and not how many of their contacts attended that school), so we chose an approach that we could easily calibrate using our survey data.↩︎
- This is typically a small number of students. In a model iteration, the median percentage of students who end up attending a school outside of their choice set ranges from 0% to around 4.1%, depending on the city↩︎
- Based on census data from 2017, Osorno, Punta Arenas, Vallenar and Salamanca had 147,666, 123,403, 45,298, and 13,520 inhabitants, respectively. Between 2003 and 2016, birth rates per 1,000 population dropped in the provinces where the four cities are located (from 14.2 to 12.2 in Osorno’s province, from 13.4 to 11.5 in Punta Arena’s, from 14.7 to 13.3 in Vallenar’s and from 13.5 to 11.6 in Salamanca’s (Instituto Nacional de Estadisticas 2005, 2018). However, as shown in Table 1, during the period 2004-2016, the number of first-grade students only declined in Osorno and Punta Arenas.↩︎
- In some specific cases where there was not enough data for the period 2004-2016, we incorporated data from other years to calibrate some of the model’s rules. See Appendix C for further details.↩︎
- In the model, the equivalent to a school’s standardized achievement test score is the mean achievement of its students.↩︎
- Experiment 6 was not simulated for the case of Salamanca. Thus, the number of runs was \(11,700\) \((3 \cdot 10 \cdot 300 + 1 \cdot 9 \cdot 300).\)↩︎
- Note that by the end of experiments 3 and 4 simulations, the cumulative change in public schools’ value-added amounts to 0.36 standard deviations. Considering that the gap between the schools with the highest and lowest value-added is 0.45, 0.4, 0.35, and 0.16, in Osorno, Punta Arenas, Vallenar, and Salamanca, respectively, this scenario drastically changes the relative position of a school’s quality. Moreover, it also changes the public schools’ quality relative to private voucher schools: private voucher schools, on average, exhibit value-added between 0.01 and 0.12 standard deviations higher than their public counterparts, depending on the city. In Experiment 3 that number is in the range of 0.21 to 0.31 standard deviations. Conversely, in Experiment 4, the mean public schools’ value-added is between 0.09 and 0.18 standard deviations above that of private voucher schools.↩︎
- This creates a stable proportion of economically disadvantaged students and similar budget constraints for students born in different years. Given that the students of the initial population attending different grades might have different average EL, the average population’s EL is fixed to match the average EL of 6th-grade students in 2004 for the whole simulation.↩︎
- Note that to be part of the choice set, the school has to offer the grade-level that the student requires and the student has to receive information about it and be able to afford it.↩︎
- Estimates of Equation 3 in the baseline scenario resulted in different signs across preference classes for \(\beta_{c2}\). To avoid a situation where applying a multiplier resulted in increasing divergence across preference classes, in experimental condition C2, we adjusted students’ preferences regarding schools’ mean achievement to guarantee that every student values this particular feature positively. More specifically, for each preference class, we set the parameter equal to the value from the class that placed the highest importance on this variable; then, this parameter was multiplied by 0, 2, 3, 4, or 5.↩︎
- See note 7.↩︎
- Students can afford schools whose tuition is lower or equal to their budget constraint. Economically disadvantaged students also can afford schools that were participating in the SEP program in said year. Additionally, we discard the previous school from the choice set, to avoid a student who decided to switch school choosing again the same school. If there were a student with an empty choice set, the model includes their closest affordable school that offers the grade level required in their choice set.↩︎
- Appendix C, in the section "Student’s Achievement Progression" describes how we estimated schools’ value-added.↩︎
- Measured as the average students’ score in Math and Language standardized achievement tests.↩︎
- Although the educational level of a school’s initial students comes from a normal distribution, the value of EL changes during the setup procedure in order to match the spatial distribution of the variable in a particular city. Both this EL variable and the economically disadvantaged attribute determine the student’s budget constraint. Consequently, the distribution of student’s ability to pay for schooling becomes right-skewed. See details in Appendix A, Phase 3, step 3.↩︎
- We used data from the student cohorts that took the test both in 4th and 8th grades, which correspond to those who were in 4th grade in the years 2005, 2007, 2009, 2010, 2011, or 2013, and students who took it both in 8th and 10th grade, corresponding to those attending 8th grade in the years 2002, 2004, 2008-2014.↩︎
- The survey’s sample size by city was not large enough to assume more classes.↩︎
- We used data from students who took SIMCE test in 4th, 8th or 10th grade between 2009 and 2012 because this is the only period of time where the survey included the necessary question.↩︎
- 2012 is the first considered year because it is the first year where the SEP program was in place for every grade level.↩︎
- Given that restricting the survey data to the cases we could link with administrative data decreased the sample size by city, this allowed us to have more reliable parameters’ calibration. This implies the assumption that the relation between the type of student (economically disadvantaged student or not) and their EL with the budget constraint does not vary across the country.↩︎
- We call it “observed” because if a household is willing to pay \(X\) for a tuition we can only observe \(X\) if there is a school with a said price; otherwise, we will observe a value lower than \(X\).↩︎
- The randomly selected school to be copied cannot be one of these new schools created in previous iterations of the model.↩︎
References
BARGIGLI, L., Caiani, A., Riccetti, L., & Russo, A. (2016). A simple model of business fluctuations with heterogeneous interacting agents and credit networks. In A. Caiani, A. Russo, A. Palestrini, & M. Gallegati (Eds.), Economics with Heterogeneous Interacting Agents. A Practical Guide to Agent-Based Modeling. Berlin Heidelberg: Springer. [doi:10.1007/978-3-319-44058-3_2]
BELLEI, C., González, P., & Valenzuela, J. P. (2010). Fortalecer la educación pública: Un desafío de interés nacional. In C. BELLEI, D. Contreras, & J. P. Valenzuela (Eds.), Ecos de la revolución Pingüina. Santiago, Chile: Pehuén.
BELLEI, C., & Munoz, G. (2023). Models of regulation, education policies, and changes in the education system: A long-term analysis of the Chilean case. Journal of Educational Change, 24(1), 49–76. [doi:10.1007/s10833-021-09435-1]
CANALS, C. (2016). Choice system en Chile: Determinantes del cambio de escuela. Calidad En La Educación, 45, 174–206. [doi:10.4067/s0718-45652016000200006]
CANALS, C., Aguirre, C., Blanco, C., Fábrega, F., Mena, C., & Paulus, N. (2019). El "Voucher" a la chilena. Reflexiones sobre elección escolar y financiamiento educacional. Estudios Pedagógicos, XLV(1), 137–150. [doi:10.4067/s0718-07052019000100137]
CANALS, C., Maroulis, S., Canessa, E., Chaigneau, S., & Mizala, A. (2022). Mechanisms underlying choice-set formation. The case of school choice in Chile. Social Science Computer Review, 41(5). [doi:10.1177/08944393221088659]
CANALS, C., Meneses, F., & Serra, C. (2015). Aspectos geográficos de los cambios de estudiantes entre establecimientos escolares. Estudios de Política Educativa, 1.
CANESSA, E., Chaigneau, S., & Marchant, N. (2023). Use of agent-Based modeling (ABM) in psychological research. In T. Veloz, A. Khrennikov, B. Toni, & R. Castillo (Eds.), Trends and Challenges in Cognitive Modeling. An Interdisciplinary Approach Towards Thinking, Memory and Decision-Making Simulations (pp. 7–20). Berlin Heidelberg: Springer. [doi:10.1007/978-3-031-41862-4_2]
CENTRO de Estudios MINEDUC. (2015). El efecto de la Ley SEP en la distribución de la matrícula escolar respecto a su dependencia. Available at: https://biblioteca.digital.gob.cl/handle/123456789/257.
CUMMINGS, P. M. M., Mizala, A., & Schneider, B. R. (2023). Chile’s Inclusion Law: The arduous drive to regulate an unequal education system, 2006-19. Educational Review, 2023. [doi:10.1080/00131911.2023.2234661]
DIXON, P., Humble, S., & Toole, J. (2017). How school choice is framed by parental preferences. Economic Affairs, 37(1), 53–65. [doi:10.1111/ecaf.12214]
DÍAZ, D. A., Jiménez, A. M., & Larroulet, C. (2019). An agent-based model of school choice with information asymmetries. Journal of Simulation, 15(1–2), 130–147.
ELACQUA, G., Iribarren, M. L., & Santos, H. (2018). Private schooling in Latin America: Trends and public policies. [doi:10.18235/0001394]
FARRE, L., Ortega, F., & Tanaka, R. (2018). Immigration and the public-private school choice. Labour Economics, 51(184), 184–201. [doi:10.1016/j.labeco.2018.01.001]
FLORES, B. (2020). Estimating the effects of school subsidies targeted at low-Income students: Evidence from Chile. Series de Documentos de Trabajo, Facultad de Economía y Negocios, Universidad de Chile.
GHAFFARZADEGAN, N., Larson, R., & Hawley, J. (2017). Education as a complex system. Systems Research and Behavioral Science, 34(3), 211–215. [doi:10.1002/sres.2405]
GRIMMELIKHUIJSEN, S., Jilke, S., Olsen, A. L., & Tummers, L. (2017). Behavioral public administration: Combining insights from public administration and psychology. Public Administration Review, 77(1), 45–56. [doi:10.1111/puar.12609]
HARLAND, K., & Heppenstall, A. J. (2012). Using agent-Based models for education planning: Is the UK Education System agent based? In A. J. Heppenstall, A. T. Crooks, L. M. See, & M. Batty (Eds.), Agent-Based Models of Geographical Systems (pp. 481–498). Berlin Heidelberg: Springer. [doi:10.1007/978-90-481-8927-4_23]
INSTITUTO Nacional de Estadísticas. (2005). Anuario de estadísticas vitales 2003. Santiago, Chile.
INSTITUTO Nacional de Estadísticas (2018). Estadísticas vitales. Informe anual 2016. Santiago, Chile.
JACOBSON, M. J., Levin, J. A., & Kapur, M. (2019). Education as a complex system: Conceptual and methodological implications. Educational Researcher, 48(2), 112–119. [doi:10.3102/0013189x19826958]
JUNEJA, N. (2007). Private management and public responsibility of education of the poor: Concerns raised by the ’Blocked Chimney’ theory. Contemporary Education Dialogue, 5(1), 7–27. [doi:10.1177/0973184913411153]
LADD, H. F., & Fiske, E. B. (2020). International perspectives on school choice. In M. Berends, A. Primus, & M. G. Berlin Heidelberg: Springer (Eds.), Handbook of Research on School Choice (pp. 87–100). London: Routledge. [doi:10.4324/9781351210447-7]
LARA, B., Mizala, A., & Repetto, A. (2011). The effectiveness of private voucher education. Educational Evaluation and Policy Analysis, 33(2), 119–137. [doi:10.3102/0162373711402990]
LEONI, S. (2022). An agent-Based model for tertiary educational choices in Italy. Research in Higher Education, 63(5), 797–824. [doi:10.1007/s11162-021-09666-4]
LOEB, S., & Valant, J. (2020). Economic perspectives on school choice. In M. Berends, A. Primus, & M. G. (Eds.), Handbook of Research on School Choice (pp. 3–16). London: Routledge. [doi:10.4324/9781351210447-1]
MACAL, C. M., & North, M. J. (2010). Tutorial on agent-based modelling and simulation. Journal of Simulation, 4(3), 151–162. [doi:10.1057/jos.2010.3]
MANZO, G. (2013). Educational choices and social interactions: A formal model and a computational test. In E. Birkelund (Ed.), Class and Stratification Analysis (pp. 47–100). Leeds: Emerald Group Publishing Limited. [doi:10.1108/s0195-6310(2013)0000030007]
MAROULIS, S. (2016). Interpreting school choice treatment effects: Results and implications from computational experiments. Journal of Artificial Societies and Social Simulation, 19(1), 7. [doi:10.18564/jasss.3002]
MAROULIS, S., Bakshy, E., Gomezc, L., & Wilensky, U. (2014). Modeling the transition to public school choice. Journal of Artificial Societies and Social Simulation, 17(2), 3. [doi:10.18564/jasss.2402]
MAROULIS, S., Guimerà, R., Petry, H., Stringer, M. J., Gomez, L. M., Amaral, L. A. N., & Wilensky, U. (2010). Complex systems view of educational policy research. Science, 330(6000), 38–39. [doi:10.1126/science.1195153]
MIERES Brevis, M. (2020). La dinamica de la desigualdad en Chile: Una mirada regional. Revista de Análisis Económico, 35(2), 91–133. [doi:10.4067/s0718-88702020000200091]
MILLINGTON, J., Butler, T., & Hamnett, C. (2014). Aspiration, attainment and success: An agent-Based model of distance-Based school allocation. Journal of Artificial Societies and Social Simulation, 17(1), 10. [doi:10.18564/jasss.2332]
MINEDUC. (1997). Ley 19532. Crea el regimen de jornada escolar completa diurna y dicta normas para su aplicación.
MINEDUC. (2004). Ley 19979. Modifica el régimen de Jornada Escolar Completa diurna y otros cuerpos legales.
MINEDUC. (2019a). Ley 20845. De inclusión escolar que regula la admisión de los y las estudiantes, elimina el financiamiento compartido y prohíbe el lucro en establecimientos educacionales que reciben aportes del estado.
MINEDUC. (2019b). Ley 21040. Crea el sistema de educación pública.
MIZALA, A., & Torche, F. (2012). Bringing the schools back in: The stratification of educational achievement in the Chilean voucher system. International Journal of Educational Development, 32(1), 132–144. [doi:10.1016/j.ijedudev.2010.09.004]
MOUSUMI, M. A., & Kusakabe, T. (2019). The dilemmas of school choice: Do parents really “choose” low-fee private schools in Delhi, India? Compare, 49(2), 230–248. [doi:10.1080/03057925.2017.1401451]
MUSSET, P. (2012). School choice and equity: Current policies in OECD countries and a literature review. OECD Education Working Papers.
NÚÑEZ, C. G., Cubillos, F., & Solorza, H. (2015). El cierre de las escuelas rurales en Chile: La escuela desplazada al no lugar. Arquitectonics: Mind, Land & Society, 27, 107–113.
OECD. (2020). PISA 2018 Results. Effective policies, succesful schools. Volume V. OECD Publishing. Available at: https://www.oecd.org/publications/pisa-2018-results-volume-v-ca768d40-en.htm
PAREDES, R. D., & Pinto, J. I. (2009). ¿El fin de la educación pública en Chile? Estudios de Economía, 36(1), 47–66. [doi:10.4067/s0718-52862009000100003]
PARMA, A. (2022). Who choose private schools in a free choice institutional setting? Evidence from Milan. Italian Journal of Sociology of Education, 14(3), 255–282.
RACZYNSKI, D., Salinas, D., De la Fuente, L., Hernández, M., & Lattz, M. (2010). Hacia una estrategia de validación de la educación pública municipal: Imaginarios, valoraciones y demandas de las familias (informe final de investigación). Fondo de Investigación y Desarrollo en Educación, Ministerio de Educación.
REARDON, S. F., Baker, R., Kasman, M., Klasik, D., & Townsend, J. B. (2018). What levels of racial diversity can be achieved with socioeconomic-Based affirmative action? Evidence from a simulation model. Journal of Policy Analysis and Management, 37(3), 630–657. [doi:10.1002/pam.22056]
REARDON, S., Kasman, M., Klasik, D., & Baker, R. (2016). Agent-based simulation models of the college sorting process. Journal of Artificial Societies and Social Simulation, 19(1), 8. [doi:10.18564/jasss.2993]
STOICA, V. I., & Flache, A. (2014). From Schelling to schools: A comparison of a model of residential segregation with a model of school segregation. Journal of Artificial Societies and Social Simulation, 17(1), 5. [doi:10.18564/jasss.2342]
TUMMERS, L. (2022). Nudge in the news: Ethics, effects, and support of nudges. Public Administration Review, 83(5), 1015–1036. [doi:10.1111/puar.13584]
VERGER, A., Moschetti, M., & Fontdevila, C. (2018). The expansion of private schooling in Latin America: Multiple manifestations and trajectories of a global education reform movement. In K. J. Saltman & A. J. Means (Eds.), The Wiley Handbook of Global Educational Reform. Hoboken, NJ: John Wiley & Sons. [doi:10.1002/9781119082316.ch7]
WILENSKY, U. (1999). NetLogo. Center for Connected Learning and Computer-Based Modeling, Northwestern University, Evanston, IL. Available at: http://ccl.northwestern.edu/netlogo/
WORLD Bank. (2022). Birth rate, crude (per 1,000 people) - Chile. Available at: https://data.worldbank.org/indicator/sp.dyn.cbrt.in?locations=CL.
ZAPATA, I. (2010). El impacto del paro de profesores en la matrícula de los establecimientos municipales. of Economics, Pontificia Universidad Católica de Chile, PhD Thesis.