A Behavioural Agent-Based Model for Housing Markets: Impact of Financial Shocks in the UK

, , ,
and
aUniversity of Glasgow, United Kingdom; bUniversity of Surrey, United Kingdom
Journal of Artificial
Societies and Social Simulation 27 (4) 5
<https://www.jasss.org/27/4/5.html>
DOI: 10.18564/jasss.5518
Received: 26-Jan-2024 Accepted: 03-Oct-2024 Published: 31-Oct-2024
Abstract
The housing market in the UK features a mortgaging system where interest rates are either fixed for short periods (typically 2 or 5 years) or varied to track interest rates of the Bank of England base rate. The reactions of home buyers and investors to changes in the mortgage rate have impacts on the buy-to-let housing market, and this in turn impacts tenants who are renting from private landlords. Such reactions become more significant when there are financial shocks, as occurred in 2022, which create chain events that can affect house prices and rents. To explore the dynamics of the UK housing market, we introduce an Agent Based Model (ABM) featuring interactions between the mortgage, buy-to-let and rental housing markets. We use the model to understand the effects of interest rate and maximum loan-to-value shocks. The ABM demonstrates the complex associations between such shocks, house prices and rents. It shows that a sudden increase in mortgage interest rates decreases housing prices and steeply increases rent prices within 5 years. It also shows that a sudden decrease of the loan-to-value ratio significantly decreases housing prices.Introduction
Housing is a critical sector of the economy that encompasses a significant portion of households’ wealth and income. Mortgaging systems are commonly applied to finance house purchases, creating interconnections between financial markets and housing markets (Campbell 2013). Across different economies, the mortgaging financial restrictions in terms of Loan-To-Value (LTV) ratios, interest rates and the temporality of agreed rates vary. The UK housing market — similar to Australia, Ireland and Spain — is structured around short term fixed rate or variable rate mortgages depending on the type of purchase (Cloyne et al. 2019; Lea 2010). Home buyers mostly acquire repayment mortgages (repayments pay towards interest and borrowed capital), whereas investors in the Buy-To-Let (BTL) market predominantly acquire interest-only mortgages (repayments pay towards interest), whereas both investors and home buyers have access to fixed interest rates mortgages for typically 2 to 5 years after which the repayments are updated based on the current interest rates. These temporal ties between interest rates and mortgages create short-term spillover effects between financial and housing markets. The underlying behavioural dynamics of the actors within the housing market play a role in shaping these spillover effects — this in turn affects the decisions of such actors. It is therefore challenging to understand the impacts of financial shocks on housing markets without considering home buyers’, investors’ and tenants’ behaviours.
To address this challenge, we introduce an Agent Based Model (ABM) featuring the interactions between the market actors within three segments of the housing market: mortgage, BTL and rental markets. The ABM is an extension of Gilbert et al. (2009)‘s housing model. It adds: (1) a rental and a BTL housing market; (2) tenants and investors; and (3) interactions that allow agents to shift between being a tenant, a home buyer and an investor over their life time. We make assumptions informed by the current UK housing market about interest rates, maximum LTV ratios and the behaviours of agents. We use the ABM to investigate the effect of agents’ behaviours on the housing market conditions when financial shocks occur. A set of experiments are structured with sudden changes to (1) interest rates and (2) LTV. These experiments are inspired by the recent shocks in the UK financial markets and the relatively sudden increase in interest rates (Chowdhury & Mosley 2023). We assess the house prices, rents, the number of sellers and buyers in the market and the number of households in the simulation. The model shows changes in housing prices and rents driven by agents’ behaviours in reaction to changes in interest rate and LTV. It also shows a lag effect in some cases between changes in house prices and their spillover into rents. With such findings, we aim to showcase the relevance of modelling the behaviours of actors in the UK housing market. We also aim to highlight some expected trends in the UK housing market while respecting that the ABM is an exploratory model rather than one closely calibrated to a specific locality.
In the next section, we provide a brief background description of the UK housing market with a focus on the English market procedures. We also introduce ABMs and their relevance to modelling housing markets. In the Model Description section, we introduce the ABM following the template proposed by Dilaver & Gilbert (2023). We highlight the aim of the model, its state variables, the agents’ intentions, actions and interactions, and the temporality of the model. We then introduce the parameters of the ABM experiments and frame them as exploratory scenarios within the UK housing market. In the Results section, we describe the model outcomes and highlight the chain of events that lead to them. Finally, in the Conclusion, we reflect on the interconnections between the financial and housing markets, and we highlight some model limitations and ways forward for further research.
Background
The housing market in England, UK
Within the UK, the regulations and procedures differ between the four nations. We focus on the English housing market for consistency. The UK housing market is structured around fixed-rate and variable mortgage interest rate regulations. It is characterised by a high frequency of selling and buying houses depending on the households’ financial situation ("climbing the housing ladder") commonly without a bidding process; for instance in 2021-2022, only 14 percent of households in the UK had been living in their currently owned home for less than 3 years (DLUHC 2022). Based on the type of buyers, the UK housing market can be divided into an investors’ BTL market and a home buyers’ market. Home buyers enter the market once they have (1) enough capital to cover a deposit for their home and (2) an income that can sustain paying for a mortgage. The amount of capital needed for a purchase is set by mortgage providers who offer different LTV ratios and interest rates. The LTV is the proportion of the market price of a house that a buyer can take as a loan (i.e., as a mortgage). In England, LTV ranges can be as high as 95 percent (Bank of England 2023c). Lower LTV ratios can be acquired if households qualify and have enough capital to cover more than 5 percent of the value of the house. The mortgage has to be repaid over an agreed period. During the early 2000s, this was usually 25 years; however, longer periods are becoming more common — in 2019, more than 40 percent of the mortgages for first time home buyers in the UK were for more than 30 years (UK Finance 2019). During the agreed period, the mortgage is paid in monthly installments that include interest. The interest paid depends on the Bank of England’s (BoE) official base interest rates, the deposit and the mortgage duration. During the first 2 to 10 years of the mortgage, it is common to have a fixed interest rate; approximately 50 percent of the agreed mortgages in 2019 started with a fixed rate for at least 5 years (Bank of England 2020). After the fixed rate period, the interest rate varies depending on the BoE’s base rate unless the home buyer reaches a new fixed rate agreement with the mortgage provider (remortgaging).
BTL investors purchase houses to rent them to tenants, with the intention of making an income from the difference between the rent and their interest payments, and also possibly accumulating capital if house prices go up. BTL mortgages were introduced in 1996, and they now constitute 9 percent of mortgages (Bank of England 2023a). The key differences from home owners’ mortgages are the rent requirements, LTV and interest rates. Securing a BTL mortgage requires proving that the expected rent from the purchased house can cover the repayments in addition to housing maintenance costs. The rent to repayment ratio ranges from 125 to 167 percent depending on the tax paying rate of the landlord — the majority of lenders require the rent is 145 percent of the value of monthly repayments (Bank of England 2023a). The LTV ratios are lower in the BTL market where mortgage providers require a deposit between 25 and 40 percent of the value of the house (Bank of England 2023c). The interest rate values are slightly higher than in the mortgage market. For instance, in September 2023, the average mortgage rate was 5.24 percent for home buyers and 5.62 percent for prospective landlords (Bank of England 2023c).
The financial link between the BoE base interest rates and mortgage rates creates potential spillover effects in housing markets during financial shocks. It also affects how home buyers and landlords make their house purchase decisions. Housing market simulations, particularly ABMs concerned with such markets, are a useful tool to explore and analyse housing market dynamics. We introduce such ABMs hereafter.
Agent-based models and housing markets
ABMs are a useful tool for modelling markets as a collection of interactions between individuals/groups with agency that exchange commodities. These models are capable of representing interactions between market actors with different degrees of granularity (Parker et al. 2012). Within housing and land market ABMs, the granularity depends on how buyers and sellers are represented and how the bidding process is implemented. They can be categorised into four levels based on how buyers, sellers and bidding are represented: (1) non-budget bound buyers only (e.g. Brown et al. 2004); (2) non-budget bound buyers with bidding (e.g. Ligmann-Zielinska 2009); (3) budget bound buyers restricted by sellers’ prices (e.g. Gilbert et al. 2009; Axtell et al. 2014; Gamal et al. 2023); and (4) bidding budget bound buyers restricted by sellers’ prices (e.g. Magliocca & Walls 2018; Zhuge & Shao 2018). The market abstraction level, alongside agents’ heterogeneity, affects the model outcomes in terms of price values and spatial distributions (Huang et al. 2013).
The choice of the level of market abstraction depends on the context of applying an ABM and its development aims. Aims can include understanding market interactions (Pangallo et al. 2019), making market predictions (Evans et al. 2021) and exploring policy scenarios (Filatova et al. 2011). ABMs concerned with housing inherit these broad aims and market representation levels, with the residential units being the non-homogeneous commodity of exchange. They can be grouped into two categories: data-informed and data-driven ABMs.
Data-informed ABMs are based on empirical evidence and expert judgements to determine the behaviour of agents. While housing ABMs in this category may be loosely based on real housing markets (e.g. Ge & Furtado 2023; Bonakdar & Roos 2023), they do not aim to mirror any actual empirical market. Examples are models that explore the links between housing and labour markets (Ge & Furtado 2023), demographic configurations (Bonakdar & Roos 2023), residential development plans (Prunetti et al. 2021) and house price patterns (Gilbert et al. 2009; Korn & Yilmaz 2022). Data-driven ABMs are strictly calibrated with data to fit an application in a specific context (Jiang et al. 2021). The outcomes and patterns from such models are not transferable as the interactions and market behaviours are context specific (Tarne et al. 2022). The aims of these models can overlap with exploratory ones (e.g. Harré et al. 2021), although in most cases they focus on policy testing (Laliotis et al. 2020; Ozel et al. 2019).
Macroprudential policies have been a focus for empirical housing ABMs. These ABMs aim to identify the impact of financial policies on prices, rents and homeowners’ wealth/debt. In doing so, they structure the financial macroeconomic dimensions of housing markets, including interest rates and maximum LTVs, and frame agent behaviours around a set of financial restrictions. These restrictions are due to the limited income and wealth of agents that dictate their capacity to acquire mortgages based on the interest rates and LTVs. These ABMs have been implemented in numerous contexts and tested across many policies. To exemplify, Geanakoplos et al. (2012) and Axtell et al. (2014) have introduced a data driven US housing market ABM where they illustrate how changes in LTV triggered the US housing crisis. Ge (2014) and Ge (2017) developed a US housing market ABM to identify the reasons for the collapse of housing prices between 2007 and 2009. This ABM tests the dynamics between lenient mortgaging policies and the emergence of housing bubbles. Mérő et al. (2023) calibrated a housing ABM for the Hungarian housing market. The model tests the impacts of construction cost shocks in parallel to fiscal policies to support families. Cokayne (2019) applied a calibrated ABM to the Danish housing market. The model investigates the effectiveness of interest rate and LTV restrictions, and concludes that stricter incorporation of fiscal policies reduces house price fluctuations.
Such ABMs have also been implemented in the UK. Baptista et al. (2016) developed a data driven ABM for the UK housing market. The ABM includes agents interacting in rent, mortgage and buy-to-let housing markets. The model investigates the impacts of limiting the Loan To Income (LTI) values, and shows that this shortens housing price bubbles cycles. The model was extended to conduct policy experiments relating to LTV caps on first-time buyers, second-time buyers and subsequent ones (Tarne et al. 2022). It shows that LTV caps significantly impact wealth distributions leading to higher economic inequalities. Another extension added age restrictions to examine the effects on LTV and LTI policies, while simplifying the dynamics around interest payments and deposits (Carro et al. 2023). The extension shows that LTI limit policies can spillover in terms of pricing to the rent market. While these UK housing ABMs explore LTV and LTI policies, they do not consider the impacts of exogenous interest rate shocks on the housing market.
An exogenous financial shock that significantly affected interest rates and LTV occurred in the UK in 2008. This shock significantly increased the proportion of households opting for higher band LTV mortgages. For instance, due to the decrease in housing prices in 2008, 17 percent of the households with secured debt had an effective LTV above 75 percent — compared to only about 7 percent in 2005 (Hellebrandt et al. 2008). More recently, the UK financial markets have experienced large changes in interest rates (Chowdhury & Mosley 2023), resulting in a rise in mortgage interest rates for new two-year fixed rate mortgages from 1.57 percent in January 2022 to 5.94 percent in September 2023 (Bank of England 2023b). Further, revert-to-rate mortgage (i.e., reverting to current rate after the fixed rate period ends) interest rates increased from 3.67 percent in January 2022 to 8.05 percent in November 2023 (Bank of England 2023c). The last time such high borrowing costs were experienced in the UK was in 1998 when mortgage interest rates reached a peak of 8.87 percent. The more recent high rates were coupled with historically high house prices, reaching a mean of £291,385 in September 2023 (Office for National Statistics 2023b). The behaviours and reactions of landlords, tenants and homeowners in such conditions remain unexplored within the UK fixed rate mortgage system. Against this background, it is timely to introduce an ABM simulating interest rates and LTV shocks in the UK housing market to investigate their impacts on households’ finances and house prices.
Model Description
The ABM is intended to help with investigating the impact of financial shocks on house prices resulting from agent behaviours. The model has been developed in NetLogo (Wilensky 1999) as an extension to Gilbert et al. (2009). The model structure and agent behaviours are informed by the characteristics of the UK housing market — with a market constituted of budget bound buyers acquiring residential units without a bidding process. The agents interact within an abstract square grid representing land units. Details of the agents, their behaviours and interactions are described hereafter.
Agents
The model includes two types of agents: (1) households; and (2) realtors.1 Households represent family units that occupy houses. There are two types of households: (a) those who are buying their house using a mortgage (or who have had a mortgage that is now paid off); and (b) those who are renting from a private landlord (housing associations and public (local authority) landlords are not included in the model). Mortgage households occupy a ‘mortgage house’, and rental households occupy a ‘rent house’. Houses represent spatial entities with no agency that can be occupied by households. Each house takes up a square of the model space, and each square can include one house at most. Mortgage houses are owned and occupied by a household agent (owner). Rent houses are owned by a mortgage household (considered as the landlord of the rent house) and occupied by another rent household (the tenant). Landlord agents must own both their homes and the house or houses that they rent out. Households can switch types under specific conditions, and they can modify the types of houses as mentioned in the "Actions and Interactions" section. Realtors represent estate agents who assess the price of the houses that they sell and put them on the market initially at that price. They have access to records that retain information about their previous transactions (sales, purchases and house prices) in the housing market.
State variables and heterogeneity
Households, houses, realtors and records each have a set of state variables, and the ABM includes a set of global variables as described in Table 1.
| State variable | Label | Description | Type | ||
|---|---|---|---|---|---|
| Household | income* | Yearly income | int | ||
| capital | \(c\) | Total accumulated savings | int | ||
| my-ownership* | Set of owned houses | list{house} | |||
| my-house* | Currently occupied house | house | |||
| mortgage | \(m\) | Remaining mortgage of each house in my-ownership | list{float} | ||
| paid-mortgage | \(\mu\) | The amount of paid mortgage for each house in my-ownership | list{float} | ||
| repayment | \(a\) | Repayment per time step for each house in my-ownership | list{float} | ||
| rate-duration | Agreed number of time steps for the mortgage interest rate | int | |||
| rent | \(r\) | Rent paid for my current house | float | ||
| propensity* | Willingness of a household will invest in the housing market | float | |||
| market | Housing market the household is currently in as a buyer | str | |||
| Realtor | locality* | Awareness radius of realtors for houses | int | ||
| memory* | Number of previous years a realtor is aware of | int | |||
| mean-price | \( \tilde{p} \) | Mean price of houses within the locality | float | ||
| mean-rent | \( \tilde{r} \) | Mean rent of houses within the locality | float | ||
| House | price | \(p\) | Price of the house in the last market transaction | float | |
| rent | \(r\) | Rent price of the house in the last market transaction | float | ||
| my-owner* | Household owning the house | household | |||
| my-occupier* | Household currently occupying the house | household | |||
| for-sale? | Whether the house is offered for sale or not | boolean | |||
| for-rent? | Whether the house is offered for rent or not | boolean | |||
| age | Number of time steps the house has been in the system | int | |||
| demolish-age | Age at which the house is demolished | int | |||
| Record | house | House exchanged during a market transaction | house | ||
| time | Run step at which the house has been exchanged | int | |||
| price | \(p\) | Price of the house at exchange | float | ||
| rent | \(r\) | Rent price of the house at agreeing tenancy | float | ||
| Global | interest-rate | \(I.s\) | Annual interest rate on borrowing money | float | |
| propensity-threshold | propensity required for a rich household to invest in the housing market | float | |||
| occupancy-ratio | Ratio of houses occupied at initialisation | float | |||
| owners-to-tenants | Ratio of households owning a house to households on a tenancy | float | |||
| LTV | \(L\) | Maximum loan to value ratio on buying a house | float | ||
| mortgage-duration | \(d\) | Maximum mortgage duration in years | int | ||
| rate-duration-M | Maximum fixed rate duration on a normal mortgage | int | |||
| rate-duration-BTL | Maximum fixed rate duration on a buy-to-let mortgage | int | |||
| mean-income | \(\tilde{y}\) | Mean income of new households | float | ||
| wage-increase | \(W\) | Percentage of wage rise per year | float | ||
| affordability | \(\alpha\) | Maximum portion of capital used to spend on housing commodities | float | ||
| savings-M | Percentage of yearly income mortgage households save | float | |||
| savings-R | Percentage of yearly income rent households save | float | |||
| homeless-period | Maximum steps a household can remain homeless before exiting | int | |||
| on-market-period | Maximum steps a household can remain on the market | int | |||
| cool-down-period | Minimum steps a household must spend before re-entering the market | int | |||
| search-length | Number of houses a household considers when buying a house | int | |||
| construction-rate | Percentage of houses built yearly | float | |||
| entry-rate | Percentage of households randomly entering the system | float | |||
| exit-rate | Percentage of households randomly exiting the system | float | |||
| realtor-territory | Radius of the realtor’s locality | int | |||
| price-drop-rate | Percentage of prices decrease per step for houses on the market | float | |||
| rent-drop-rate | Percentage of rents decrease per step for houses on the market | float | |||
| savings-threshold-M | \(\omega\) | Factor controlling the ‘relatively rich’ threshold of mortgage households | float | ||
| evict-threshold-M | \(\beta\) | Factor controlling the ‘relatively poor’ threshold of mortgage households | float | ||
| savings-threshold-R | \(\lambda\) | Factor controlling the ‘relatively rich’ threshold of rent households | float | ||
| evict-threshold-R | \(\gamma\) | Factor controlling the ‘relatively poor’ threshold of mortgage households | float | ||
| steps-per-year | Number of steps representing each year in the model runs | int | |||
| * indicates external variables at initialisation | |||||
Households are assigned a type, a state describing whether their mortgage is fully paid or not and an income when they are introduced into the model. Their incomes are random values drawn from a gamma distribution — which approximates the distribution of income in the UK (Office for National Statistics 2024b). The initial income is then used to determine the household’s initial capital, the repayments of their mortgage or their rent, and these in turn are used to assign a price to the house in which the household lives (for details, see below). This initialisation procedure ensures that income, capital, rents, and house prices are all heterogeneous between households and are coherent for a given household. Realtors have unique spatial locations, and there are heterogeneous sets of houses within each realtor’s locality.
Intentions
A household’s intention is to keep occupying a house and avoid being homeless. Their intention extends to investing in the housing market under specific income and capital conditions (see "Actions and Interactions"). A realtor’s intention is to value house prices and rents when requested by households.
Actions and interactions
We follow the actions of each agent type at initialisation and during the runs separately. The interactions between the agents are highlighted where relevant.
Households
Households at initialisation are assigned a type and an income. They are then assigned starting values of: (1) the amount of capital they hold; (2) the house or houses they own or rent; and (3) the mortgage or rent they pay.
First, households calculate their capital as a multiple of their income as shown in Equation 1.
| \[ c_{i,t_0} = y_{i,t_0} . \eta_i\] | \[(1)\] |
Second, mortgage households randomly select one house of type mortgage to occupy, and they randomly add a set of houses of type rent to their ownership. The households update the ‘my-owner’ variable of the houses accordingly. This only stops once all houses have been assigned an owner household.
Third, to set prices, mortgage households calculate the highest repayment they can afford by comparing it to the income they are willing to spend on housing commodities as shown in Equation 2. They then determine the maximum mortgage they can pay while considering their maximum repayment and the duration of the mortgage following Equation 3. This formula is derived from Kohn (1990)’s calculation for the repayments as a function of the interest rate, the duration and the borrowed amount (see "Maximum mortgage calculation"). Based on the this maximum mortgage and the maximum loan-to-value ratio, the households calculate the deposit they have to pay according to Equation 4.
| \[ a_{i,{t_0}} = \frac{y_{i,{t_0}}.\alpha_i}{s}\] | \[(2)\] |
| \[ M_{i,{t_0}} = \frac{a_{i,{t_0}}}{I_{t_0}}.(1 - (1 + I_t)^{-d_{t_0}.s})\] | \[(3)\] |
| \[ D_{i,{t_0}} = M_{i,{t_0}} . (\frac{1}{L} - 1)\] | \[(4)\] |
Rent households calculate the rent they will be charged. Following a similar logic to Equation 2, the rent households use their spending on housing commodities to dictate the highest rent they can pay as shown in Equation 5.
| \[ b_{i,{t_0}} = \frac{y_{i,{t_0}}.\alpha_i}{s}\] | \[(5)\] |
Mortgage and Rent households then assign prices and rents for their respective houses as shown in Equations 6 and 7. Mortgage houses are assigned a price equivalent to their owners’ mortgage as calculated in Equation 3. Rent houses are assigned a rent equivalent to the highest rent the tenant can pay as long as this is higher than the owner’s repayments. Otherwise, the rent is set to the owner’s repayments, and tenants update their income to match the new rent.
| \[ p_{j|i} = M_{i,t_0} + D_{i,{t_0}}\] | \[(6)\] |
| \[\label {eq:6} r_{j|i,i^*} = \begin{cases} b_{i^*,t}\text{ ,} & \text{if } b_{i^*,t} > a_{i,t} \\ a_{i,t}\text{ ,} & \text{otherwise} \end{cases}\] | \[(7)\] |
| \[ y_{i^*} = \frac{r_{j|i,i^*}.s}{\alpha}\text{ ,} \quad \text{if } r_{j|i,i^*} = a_{i,t}\] | \[(8)\] |
Mortgage households are then assigned their actual current mortgage as a proportion of the price taking into account the loan-to-value ratio as shown in Equation 9.
| \[ m_{i,j} = L.p_j\] | \[(9)\] |
During the runs, existing households: (1) check their finances; (2) join a housing market if their finances allow it; and (3) may exit from the system if they have been unable to find a house — exiting households are not automatically replaced, rather there is an immigration rate which generates new households (immigrants) every time step. Immigrant households: (1) enter the system; and (2) join a housing market.
In more detail, existing mortgage households check their financial status considering their mortgages, repayments, normal incomes and incomes from rent. They check the two conditions in Equation 10, that: (a) their capital is higher than the median deposit needed given the median value of all their current mortgages and (b) their residual income can cover a new repayment equal to the the median of the current repayments. If these conditions are satisfied, the household is considered ‘relatively rich’. Relatively rich households have a high income and capital compared to the cost of their own house(s). This puts them in a position to become buyers in the housing market. The mortgage households also check whether their repayment is higher than their annual income including any income from rents (Equation 11). If this condition is satisfied, the household is considered ‘relatively poor’. Relatively poor households struggle with their housing finances and are in danger of defaulting on their mortgage or rent leading to possible eviction.
| \[ \begin{cases} c_{i,t} > \omega.\tilde{m}_{i,J,t}.(1-L_t) \text{ ,} & \text{where } j\in{J} \\ y_{i,t} + ((\sum_{j=1}^{n}r_{i,j}).s.\alpha_i) - \sum_{j=1}^{n}a_{i,j,t} > \tilde{a}_{i,J,t}.s \text{ ,} & \text{where } j\in{J} \end{cases}\] | \[(10)\] |
| \[ \sum_{j=1}^{n}(a_{i,j,t}.s) > \beta.\alpha_i.(y_{i,t}+\sum_{j=1}^{n}(r_j.s)) \\\] | \[(11)\] |
Relatively rich mortgage households invest in the housing market if \(w_i>\Omega\) where \(w_i\) is the probability a household invests in the housing market and \(\Omega\) is the desired investors to non-investors ratio in the model. Relatively poor mortgage households act on the basis of the number of houses they own. If the household owns one house only, the household offers the house for sale and joins the rental market. If the household owns more than one house, the household selects the house yielding the lowest surplus rent compared to its repayment. This house is evicted and placed on the rent market with an initial requested rent equal to at least the mortgage repayment of that house. After a defined period of time, if no tenant makes an offer on the house, the mortgage household decides to sell one of its owned houses on the market to increase its capital. It selects the house yielding the highest expected profit when sold on the mortgage housing market, as shown in Equation 12.
| \[ f_{i,j^*} = \begin{cases} \max_{j\in{J_{i|v}}}{(p_j - m_{i,j})} \text{ ,} & \text{if } J_{i|v}\neq\phi \\ \max_{j\in{J_{i|r}}}{(p_j - m_{i,j})} \text{ ,} & \text{otherwise} \end{cases}\] | \[(12)\] |
Rent households consider their financial situation by looking into their income, capital, expected mortgages, expected repayment and rent. They consider whether their capital is higher than the expected deposit for the house they occupy given the current LTV ratio as shown in Equation 13. If that is satisfied, they are classified as relatively rich. They also check if their rent is higher than their income as shown in Equation 14. If this is the case, they are considered to be relatively poor.
| \[ c_{i,t} > \lambda.p_{j|i}.(1-L_t)\] | \[(13)\] |
| \[ r_{j|i}.s > \gamma.\alpha.y_{i,t}\] | \[(14)\] |
Relatively rich rent households join the mortgage housing market aiming to become home owners. Relatively poor rent households join the rental market to search for a more affordable rent house.
Finally, households who do not have a house to occupy (i.e., homeless households) get discouraged from the market and leave the system after a defined period of time. Households who own a house and are on the market intending to move get discouraged after a period of time. However, they enter a cool down period before they can re-enter the housing market. The cool down state can only be terminated early in cases where the household become relatively poor or homeless. In that case, they ignore the cool down period and immediately enter the housing market.
New households entering the system are initialised with a type and an income, and they follow Equation 1 to calculate their capital. Mortgage immigrant households enter the mortgage housing market, whereas rent immigrant households enter the rent housing market. In subsequent time steps, they follow the process described above. This implies that they exit the system if they do not find a house for a defined period.
Realtors
Realtors evaluate the prices and rents of houses according to Equation 15 and Equation 16. They ensure that prices and rents do not significantly increase to more than double the previous price or decrease to less than half the previous price. It should be noted that these situations only occur in cases of extreme exogenous financial shocks during the runs.
| \[ p_{j,k,t+1} = \begin{cases} 2p_{j,t} \text{ ,} & \text{ if } \frac{\tilde{p}_{J_k}}{p_{j,t}} > 2 \\ \frac{p_{j,t}}{2} \text{ ,} & \text{ if } \frac{\tilde{p}_{J_k}}{p_{j,t}} < \frac{1}{2} \\ \tilde{p}_{J_k} \text{ ,} & \text{ otherwise} \end{cases}\] | \[(15)\] |
| \[ r_{j,k,t+1} = \begin{cases} 2r_{j,t} \text{ ,} & \text{ if } \frac{\tilde{r}_{J_k}}{r_{j,t}} > 2 \\ \frac{r_{j,t}}{2} \text{ ,} & \text{ if } \frac{\tilde{r}_{J_k}}{r_{j,t}} < \frac{1}{2} \\ \tilde{r}_{J_k} \text{ ,} & \text{ otherwise} \end{cases}\] | \[(16)\] |
Realtors decay the price of unsold mortgage houses currently on the market as shown in Equation 17 and similarly decay the rent of vacant rental properties according to Equation 18. This ensures that unaffordably high prices and rents decrease until households on the markets can make purchases.
| \[ p_{j,t+1} = \rho.p_{j,t}\] | \[(17)\] |
| \[ r_{j,t+1} = \rho.r_{j,t}\] | \[(18)\] |
Houses
At initialisation, house prices and rents are assigned according to Equation 6 and Equation 7. During the runs, realtors assign prices and rents following Equation 15 and Equation 16.
New houses are constructed at every time step, the number being proportional to the number of the houses in the system. The new houses are put on the mortgage market, and the realtors assign them prices during the market transactions. The demolition of a house is triggered if the house age is greater than its expected lifetime (a duration set at the time of its construction using a random exponential).
Records
Records save the details of transactions in the housing market. A record is created once a house is bought or sold to record the price/rent and time step.
Temporality
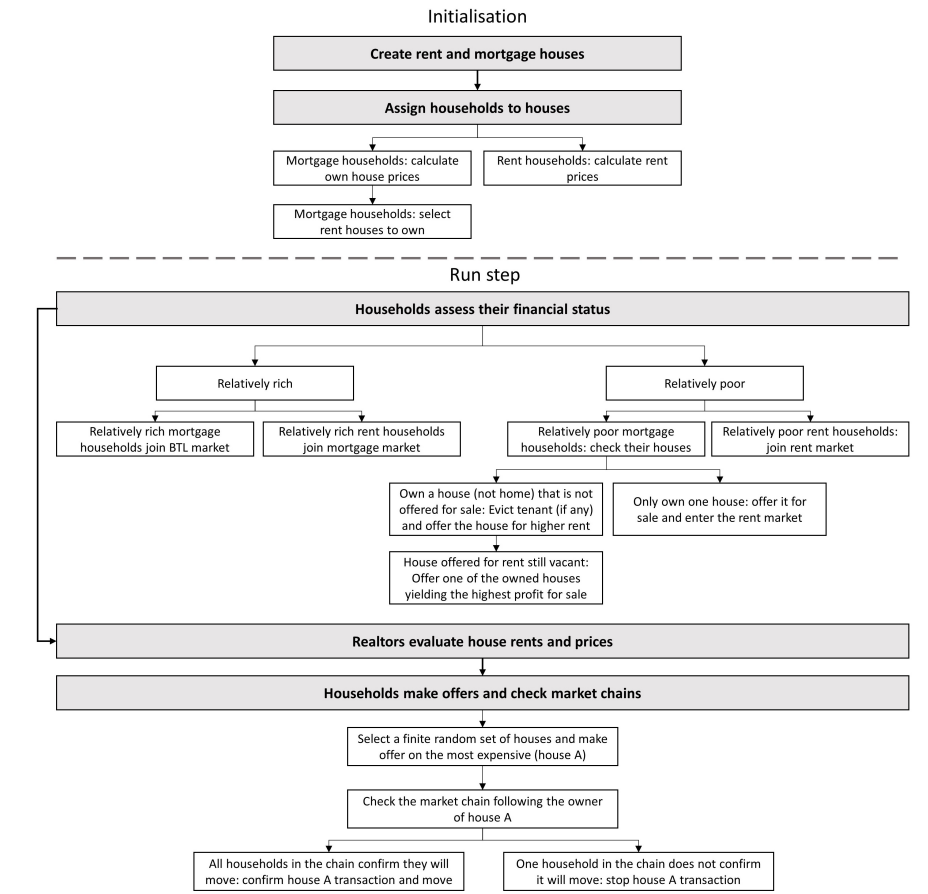
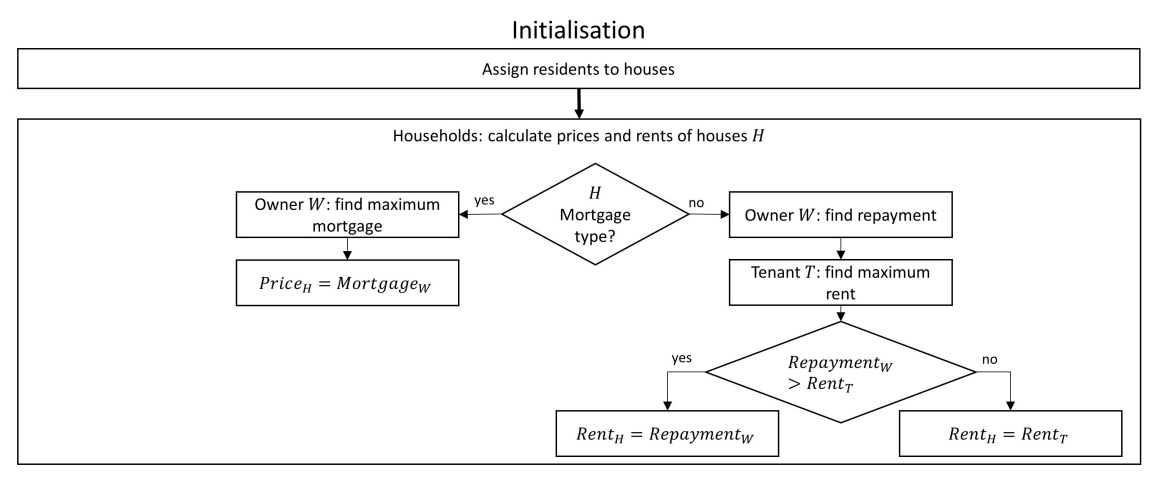
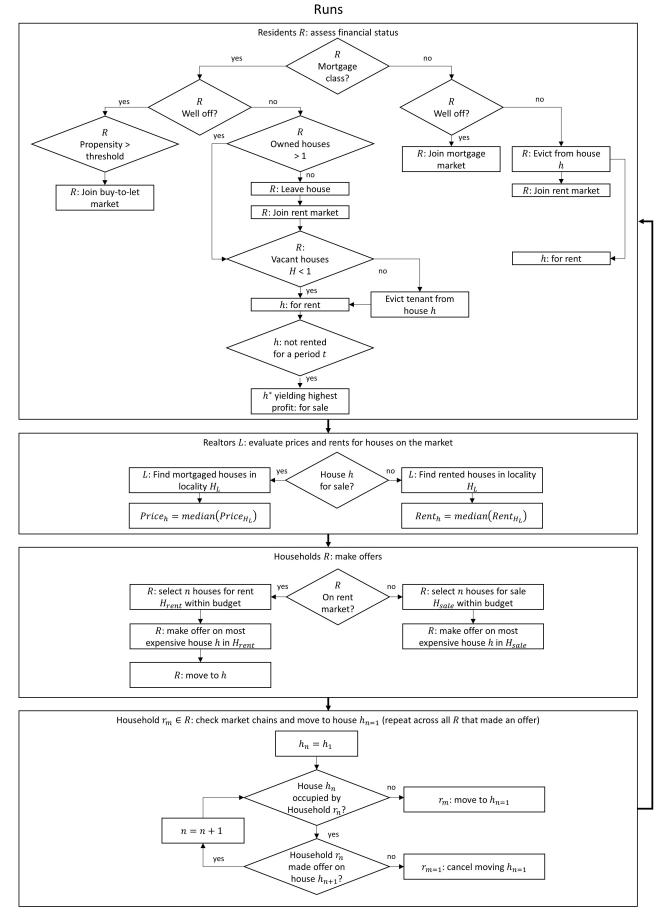
Time is advanced during model runs in steps. The number of steps per year \(s\) remains constant. At each time step, the agents make decisions and trigger actions such as moving house. Figure 1 is a flow chart showing the ABM initialisation and run schedules. More detailed flowcharts are provided in the Appendix in Figures 5 and 6.
At initialisation, houses are constructed and assigned a type (mortgage house or rent house). Households are then assigned randomly to a house, and this dictates the household’s type (owner-occupier or renter). Each household calculates the price or rent of its house (Equations 6 and 7). Each rent house is then randomly assigned to a landlord, chosen from the households occupying a mortgage house as an owner.
During the run, first, households assess their financial status. They check their capital, repayments and rents to assess whether they are relatively rich or relatively poor. Relatively rich mortgage households enter the BTL market. Relatively rich rent households enter the mortgage market to buy a home. Relatively poor mortgage households check whether they are a landlord owning a house other than their own. If not, they offer their home for sale. If they are able to sell, they leave their home and enter the rental market intending to become tenants. If they own other houses, and none of their owned houses are currently offered for sale, they choose one to put on the mortgage market. They select the one yielding the highest amount by comparing the house’s remaining mortgage to its realtor valuation price. If the house is rented, they evict the tenant before putting the house on the market.
Second, realtors evaluate all the houses on the rent and mortgage markets (Equations 17 and 18).
Third, households on the mortgage and BTL market make offers on the houses. Starting from the households on the mortgage market followed by those on the BTL market, each household randomly selects a limited number of houses within their budget. That household then selects the most expensive house and makes an offer to purchase it. The house is then withdrawn from the market as "sold subject to contract". This implies that households on the mortgage markets (home buyers) are prioritised during the market clearing process compared to those on the BTL market (investors).
Fourth, the households making the offers check the market chains before finalising the transaction. Consider a household making an offer on house \(A\). If house \(A\) is not occupied, there is no chain to check so the household confirms the purchase and moves to the house. If house \(A\) is occupied, its owner checks if it had made an offer on another house. If it made an offer on house \(B\) for instance, the market chain for house \(B\) must be checked — that is, whether house \(B\) is occupied or not and whether its owner made an offer on another house. If this last household in the chain confirms they will move to a new house, all the households in that chain can make their purchases (including the ones purchasing houses \(A\) and \(B\)).
Finally, once all the confirmed market transactions are made, households receive their income and accumulate capital. Households failing to make transactions remain on the market to try again in the next time step.
Experiments
We carry out a set of experiments to explore the effect of LTV ratios and interest rates shocks. We monitor: (1) the number of houses and households in the system, (2) the number of households on the markets; (3) house prices and rents; and (4) wealth — defined as the capital and the paid portion of the price(s) of owned house(s).
For all the experiments, we use an abstract square space that does not represent a real geographical location. Instead, house locations and realtors locations are stochastically generated for every run. This implies that the observed results are not driven by dynamics that are a unique outcome of a particular spatial initialisation structure. However, spatial clusters of high and low rents emerge across all the runs as shown in "spatial outcomes". Geo-spatial effects can be further explored by using a space representing an existing geographical location; however, this is beyond the focus of this study. The abstract space is 64 land units long and 64 wide. These dimensions are large enough to allow the market dynamics to occur and lead to consistent outcomes without requiring too much computational time (see the Appendix).
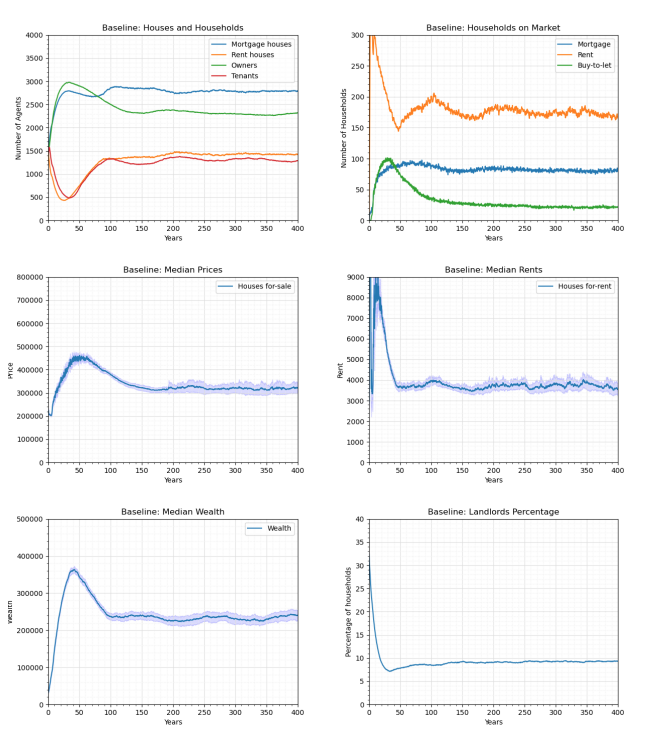
We initialise the model with the global parameters shown in Table 2. The incomes of households are drawn from a random gamma distribution truncated above and below £15,000 and £45,000 (mean £30,000). The houses are initially generated on 70 percent of the land units (i.e., 2956 initial houses), and the houses are randomly distributed in terms of their type and location as shown in Figure 2. We run the model through a stability phase for 200 years before presenting any results to ensure that the ABM reaches stable ratios of rent houses, mortgage houses, tenants and owners (see the Appendix). This helps to isolate the outcomes of the experiments from the dynamics of reaching market stability due to the initial random distribution of agents. At year 300, the interest rates and LTV ratios are modified as shown in Table 3. We let the ABM run for 100 more years (until year 400) to allow for a long enough period to observe the effects of the financial shocks.
| Parameter | Value | Source | ||
|---|---|---|---|---|
| interest-rate (\(I_t\)) | 3.7% | (Bank of England 2023a) | ||
| propensity-threshold | 0.2 | Yields 9% landlords to total population as per Figure 11-D3 (Benham and Reeves 2023) | ||
| occupancy-ratio | 95% | |||
| owners-to-tenants | 50% | |||
| LTV (\(LTV_t\)) | 90% | (Bank of England 2023a) | ||
| mortgage-duration | 25 | |||
| rate-duration-M | 2 to 5 | (Cloyne et al. 2019) | ||
| rate-duration-BTL | 1 to 5 | (Bank of England 2023b; Mortgages for Business 2020) | ||
| mean-income | 30000 | (Office for National Statistics 2023a) | ||
| wage-increase | 0 | (Office for National Statistics 2024a) | ||
| affordability (\(\alpha\)) | 33% | |||
| savings-M | 20% | |||
| savings-R | 5% | |||
| homeless-period | 5 | |||
| search-length | 5 | |||
| construction-rate | 0.6% | (Department of Levelling Up, Housing and Communities 2023) | ||
| entry-rate | 4% | |||
| exit-rate | 2% | |||
| realtor-territory | 16 | |||
| price-drop-rate | 3% | |||
| rent-drop-rate | 3% | |||
| savings-threshold-M (\(\omega\)) | 2 | |||
| evict-threshold-M (\(\beta\)) | 1 | |||
| savings-threshold-R (\(\lambda\)) | 2 | |||
| evict-threshold-R (\(\gamma\)) | 1 | |||
| steps-per-year | 4 | |||
| The values of parameters with no stated sources are assumptions by the authors | ||||
| Experiment | Label | Parameter | Value | |
|---|---|---|---|---|
| Interest rate increase at year 300 | Interest rise | \(I_0\) | 3.7% | |
| \(I_{300}\) | 8% | |||
| Interest rate decrease at year 300 | Interest decline | \(I_0\) | 8% | |
| \(I_{300}\) | 3.7% | |||
| LTV decrease at year 300 | LTV decline | \(L_0\) | 90% | |
| \(L_{300}\) | 69% | |||
| LTV increase at year 300 | LTV rise | \(L_0\) | 60% | |
| \(L_{300}\) | 74% | |||
Results
The results for each experiment are shown after the initial stability phase at year 300. As mentioned, we apply a financial shock at year 300, and then run the model until year 400 to reach a post-shock stable state. We run each experiment 20 times, and we present the mean values of the results at each time step. For rents, prices and wealth we show the range of the outcomes across the runs over a 95 percent confidence interval (e.g., Figure 3-C1). We do not represent the confidence interval in any graphs with more than one plotted outcome for readability. The observed trends immediately after the shock are economically significant and consistent; they lead to changes in purchase ability and decisions across the runs of each experiment. For the first two experiments, about the effect of interest rate shocks, we use the values 3.7 percent and 8 percent reflecting recent revert-to-mortgage rate changes in the UK. For the second two experiments, showing the effect of LTV shocks, we use LTV values of 60 percent and 90 percent as they represent the most commonly applied mortgage bands recently available in the UK housing market — noting that households in the UK can access lower LTV if they qualify and can pay a higher deposit. We set the LTV shock values to 74 percent and 69 percent because they represent the highest and lowest median LTVs across all mortgages in the UK since 2016 (Financial Conduct Authority 2024; Statista 2024). We describe the outcomes focusing on: (1) the median prices of houses offered for sale; and (2) the median rents of houses offered for rent. All prices and rents mentioned are means of median prices for the houses in the system. We also clarify the behavioural dynamics leading to the outcomes referring to: (1) the ratios of house types; (2) the number of home owners and tenants; and (3) the number of households on the mortgage and rental markets. For detailed results, see Figure 3 and Figure 4. Note that the outcome prices and rents are nominal in the ABM as wage rises and increases in spending in non-housing commodities are not simulated. This means that the ABM outcomes are already adjusted for inflation relative to the initialisation point. We further explore the impact of increasing wages on inflating the prices and rents in the within a pattern oriented modelling approach.
Interest rate experiments
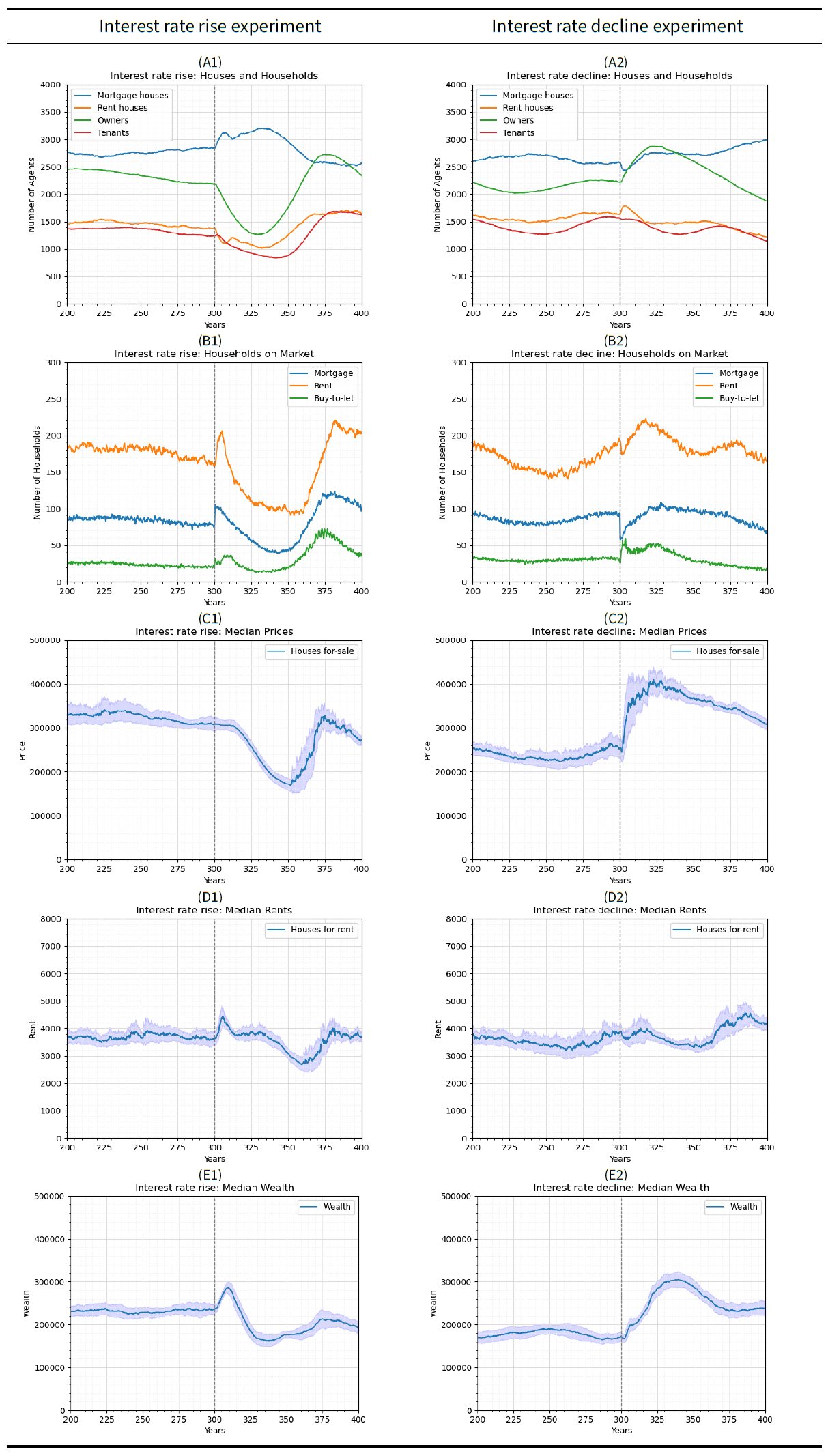
In the interest rate rise experiment, house prices (Figure 3-C1) decrease 10 years after increasing interest rates at year 300. The median price of houses offered for sale decreases for 50 years from approximately £308,000 to £172,000 (a 44.2 percent decrease) at year 350.2 The prices recover for 25 years increasing to £328,000 (90.7 percent increase) at year 375. The prices of houses for sale then enter a "periodic stable state" with waves of increase and decrease in prices (see "Periodic stabiltiy phase" for more details). The observed initial decrease in prices occurs because of the impact of interest rates on current mortgages and the maximum mortgage a new buyer can acquire. An increase in interest rate increases current repayments making home owners and landlords less likely to be ‘relatively rich’ to join the mortgage or BTL housing market. It also pushes some of them to become ‘relatively poor’, which puts more houses for sale. Relatively poor landlords evict tenants and put the houses for sale, whereas homeowners either join the mortgage market to downgrade their house and decrease repayments or sell their home, join the rent market and become tenants. These dynamics create a situation where more households join the mortgage market leading to an increase in the number of households on that market from 74 to 99 by year 303 (Figure 3-B1). Even when households are able to join the mortgage or BTL housing market, they require lower maximum mortgage values (see Equation 3) due to the high interest rates. The low borrowing capacity makes these households incapable of buying houses with sale prices set before the interest shock. As a result, houses for sale remain on the market for longer periods, allowing prices to decay. Households remain on the mortgage and the BTL housing markets either until prices are low enough for them to cover the repayments or until they get discouraged. This explains the observed slight increase in the number of households staying on the BTL market from 21 to 34 by year 310.
Rents for rent houses on the market (Figure 3-D1) increase after a lag of 3 years. They rise from £3620 to £4340 from year 303 to 305. Rents then decrease by year 315 to £3770. They then remain stable until year 335, after which they gradually decrease for 25 years reaching a minimum of £2720 at year 360. They recover to £4150 by the end of the simulation. The increase in rent prices between years 300 and 305 is explainable through a chain of events starting from landlord behaviours. The increase in interest rates leads to increases in the repayments of landlords who react by increasing rents to cover the extra costs. This directly increases rents and risks making some tenants relatively poor leading to evictions. The increase in rents and evictions of tenants have three effects: (1) the number of households in the rental market increases from 160 to 203 within 5 years; and (2) landlords struggle to find tenants who can afford the higher rents making landlords unable to cover the repayments of their vacant houses. These landlords are forced to put their vacant houses for sale rather than rent them to cover their mortgage repayment. This increases the percentage of the mortgage houses in the system from 67.23 percent to 73.33 percent from year 300 to 305. With the total number of houses in the system not increasing, this creates a situation of low numbers of houses offered for high rents and a high demand for rent houses with lower rents (due to high number of evicted households on the rental housing market). This forces landlords to reduce the rent to find tenants, which leads the observed decrease in median rent to £3770 by year 305. Hence, only landlords with a high enough income to cover their higher repayments without increasing rent significantly keep their BTL houses on the rent market. This dynamic highlights spillover effects from the mortgage and BTL housing market prices to rent prices due to variable and short-term interest rate changes. After year 315, rent prices change in reaction to the periodic changes in housing prices. Decreasing prices until year 350 means that more landlords can afford houses on the BTL market without having to enforce high rents. However, as housing prices stop decaying, higher prices force some landlords to increase rent to cover the repayments.
Wealth increases after a lag of 3 years similar to rents. The median wealth (Figure 3-E1) rises from £248,220 to 284,925 from year 303 to year 310, after which it decreases to £163,610 by year 340. It then recovers to £213,550 by year 375 after which it slightly decreases. The initial increase in median wealth is linked to higher rents that: (1) allow landlords to accumulate more wealth; and (2) push the poorest tenants outside of the system. After year 310, wealth decreases in reaction to the steep decrease in prices, which implies that all owners become poorer as the values of their houses decrease. The recovery of wealth later is also a reflection of the increase in the price of houses.
In the interest rate decline experiment, although house prices are significantly affected after the interest rate decreases, rents remain relatively unaffected. The median price of houses for sale (Figure 3-C2) increases from £252,830 to a peak of £409,000 (a 62.3 percent increase) from year 300 to 323. The price decreases to approximately £309,600 by the end of the run — prices then enter a periodic stable state in longer runs. The observed increase in prices is linked to (a) the decrease in households on the mortgage housing market (from 94 to 61) and simultaneously (b) the increase in households on the BTL market (from 32 to 53). Decreasing interest rates increases the maximum mortgage buyers can secure. This makes households more capable of buying houses at the prices set before the shock as the markets are yet to react. Therefore, households already in the mortgage and BTL markets become capable of purchasing more expensive houses. Further, some households become relatively rich and join these markets. The price offering process prioritises home buyers compared to BTL buyers. Hence, households on the mortgage market acquire houses more quickly and leave the market. In contrast, households on the BTL market remain on the market for longer periods until they face less competition from the home buyers. These dynamics allow less time for houses to remain on the market for prices to decay, which pushes house prices upwards.
Rents slightly decrease immediately after the decrease in interest rate. The median rent price of houses offered for rent (Figure 3-D2) decreases from £3860 at year 300 to £3660 at year 305, and they recover to £3845 by year 310. The immediate decrease in rent is because many tenants become relatively rich and enter the mortgage market to buy houses at lower interest rates. Subsequently, these tenants leave their rented houses and move to their recently purchased homes. This creates a system with a high number of vacant houses offered for rent with fewer households on the rent market (a decrease from 192 to 167 households). Houses offered for rent remain on the market for longer leading to a decay in median rents. However, rent prices recover quickly as the increase in prices by year 310 forces landlords to stop decreasing rents below their repayments. This remains the case until housing prices start to decay by year 320, which allows landlords to offer their houses for lower rents. These dynamics between the years 300 and 320 include a shift in the percentage of owners (from 58.75 to 66.93 percent) and tenants (from 33.07 to 41.25), alongside a significant increase in house prices. This puts the rent prices into a periodic stability phase after year 320 (see "Periodic stabiltiy phase").
Wealth increases after a minor decrease for 2 years. The median wealth (Figure 3-E2) decreases from £172,450 to £166,970 by year 302. It increases to £304,270 by year 340 after which it decreases to £231,200 by year 375 and remains stable. The initial minor decrease in wealth is due to the decrease in rents. Landlords accumulate less capital as tenants move from rent houses to new homes. After year 302, this is countered with a significant increase in house prices which increases the wealth of all the owners in the system. Wealth then decreases in reaction to the decrease in prices by year 330. The median wealth appears stable towards the end of the runs as higher rents make landlords richer, which counters the loss in wealth due to the decreasing prices.
Comparing the interest rate experiments, there is an asymmetry in changes in prices and rents despite the similar magnitude of changes in interest rate. For prices, this is because an increase in interest rate can directly force owners to become relatively poor leading to quick evictions, and this disrupts the market. In contrast, a decrease in interest rates cannot cause forced evictions, which leads to a smoother change in prices as new buyers take advantage of the lower interest rates. For rents, the asymmetry is due to the condition that landlords need to cover their repayment from their rent. In cases of interest rate rise, landlords directly intervene in setting rents high enough to cover their repayments. However, with an interest rate decline, landlords are not directly incentivised to decrease rents. This leaves the changes in rents to the realtors and the decay process due to the supply and demand dynamics in the model.
Loan to value ratio experiments
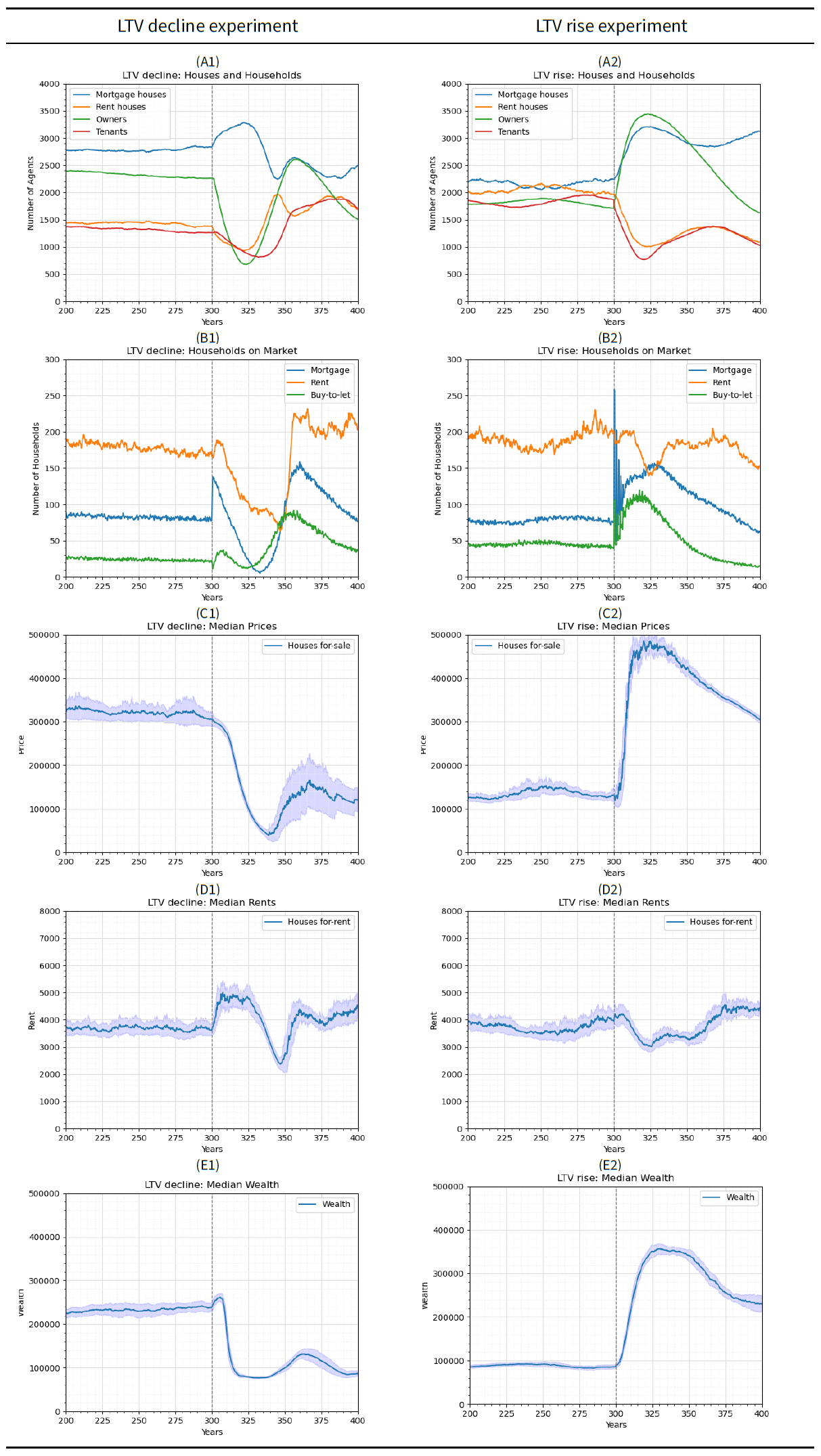
In the LTV decline experiment, house prices decrease with a decrease in LTV, whereas rents increase. The median price of houses for sale (Figure 4-C1) decreases from £305,840 to £41,970 by year 340 (an 86.28 percent decrease). The median price recovers to £154,200 by year 365. The steep decrease in prices occurs due to lower borrowing capacity with an LTV decrease. Given that the capital of households remain relatively similar after the shock, the households become less able to purchase an expensive house. More households remain on the mortgage housing market in search for an affordable house — leading to an increase of households on the mortgage housing market immediately after the shock from 79 to 136. Households already in the system do not join the BTL or mortgage housing markets because of the stricter conditions required to become ‘relatively rich’. On the long run, this contributes to a decrease in the number of households on the mortgage housing market from 136 to 5 (a 96.32 percent decrease). These dynamics remain in place until the prices of houses decay to a level that households can afford given the lower LTVs. During that decay phase, many households fail to find houses, get discouraged and leave the system, leading to a decrease in the population from 3521 to 1560 by year 325 as shown in Figure 4-A1. This severe population drop leads to later waves of prices and population changes with a periodic stability state as mentioned in the "Periodic stabiltiy phase" section.
Rent values increase immediately after the shock. The median rent prices of houses offered for rent (Figure 4-D1) increases from £3615 to £4850 by year 308. Rents remain stable until year 325 after which they decrease to £3130 (a 35 percent decrease). They then recover to £4390 by year 360, and following this they enter a periodic stable state. The initial increase in median rents is due to the lack of supply of rent houses — triggered by the decrease in the landlords’ ability to buy houses. This remains the case until year 325 when more households on the BTL market successfully buy houses and offer them for rent. This creates the first excess supply of houses for rent since year 302. New landlords buying at lower prices are not incentivised to request high rents to cover their repayments. This leads to a significant decrease in rents in alignment with the decrease in prices until year 345. Rents then increase with an increase in prices as landlords require higher rents to cover the higher repayment. The rents then enter a periodic stable state similar to the prices.
Wealth initially increases slightly after the shock, followed by a significant decrease. The median wealth (Figure 4-E1) increases from £238,060 to £260,580 (a 9.46 percent increase) by year 305. It then decreases to £81,350 (a 68.78 percent decrease) by year 320. A wave of wealth increase is observed afterwards with a peak of £130,020 at year 365. The increase in wealth right after the shock is due to landlords having higher rent that leads to the accumulation of capital in parallel to excluding tenants who cannot afford such rents. Wealth then decreases in alignment with the decrease in prices which affects owners’ wealth. The later wave of increase in wealth also aligns with a wave of increase in prices.
In the LTV rise experiment, the mean price of houses for sale (Figure 4-C2) increases from years 300 to 315 from approximately £132,320 to £459,940. The observed increase in prices is due to the higher borrowing capacity associated with quick market clearing. Higher LTV allows households to have higher mortgages with the same amount of capital. Hence, more mortgage households and tenants become ‘relatively rich’ and enter the market leading to observed spikes in the number of households on the mortgage and BTL markets. The spikes occur because the very high demand means not all households will be able to find a house before they are discouraged. These discouraged households keep re-entering the market until they are able to make a successful offer. The households on the mortgage market are prioritised during transactions compared to those on the BTL market. Hence, households on the mortgage housing market tend to find houses more quickly, leading to a quicker decrease in the magnitude of the observed spikes for the mortgage market compared to the BTL market. Aside from such spikes, the number of households on the mortgage market increases from 76 to 152 by year 325, as tenants accumulate the capital needed to become ‘relatively rich’. The number of households on the BTL market also increases from 41 to 109 by year 315. This high demand leads to a quick clearing of the houses without giving room for prices to decay, contributing to an overall increase in prices. This remains the case until year 325 when prices reach a level aligned with the mortgages households can secure (£484,990) given the higher LTV. Accordingly, the median price decreases until the end of the run while the numbers of households in the BTL and mortgage housing markets also decrease. Lower numbers of households on the mortgage and BTL markets imply a lower demand for mortgage houses which allows prices to decay. Beyond this, the prices enter a periodic stability phase associated with periodic fluctuations in the ratios of owners to tenants as partly observed in Figure 4-A2 (see "Periodic stabiltiy phase" for more details).
The median rent decreases after the shock, from £3950 to £3023 by year 325. This is because tenants become relatively rich with less capital, leading to a decrease in the number of tenants from 1863 to 827 by year 325. With the high number of households in the BTL market, the supply of houses for rent remains higher than the demand — despite households on the BTL not being prioritised compared to home buyers during the offering process. This implies houses remain longer on the rent market allowing rents to decay. After year 325, rents increase slightly from 3023 to 3454 by year 335 as prices reach their peak and landlords become forced to increase rents to cover their repayments. Rents then enter a periodic stability phase with associated periodic waves of changes in the number of owners and tenants.
Wealth changes in alignment with changes in prices. The median wealth increases from £86,260 to £350,605 by year 325 due to an increase in prices during the same period from £132,320 to£484,990. Median wealth then decreases to £230,405 by the end of the run in alignment with a similar decrease in median prices to £307,025.
By comparing the LTV rise and decline experiments, there are minor asymmetries in changes in prices and major ones for rents. For prices, the minor asymmetry is because an LTV rise leads to a significantly higher change in the number of households on the mortgage and BTL market. That is, the number of households joining the markets due to the LTV rise is higher than those leaving in case of an LTV decline of a similar magnitude. This leads to a sharper increase in prices for the LTV rise experiments. For rents, the asymmetry is due to the interaction of two dynamics: (1) the rent houses supply and demand; and (2) the restriction that landlords cover their repayments with rents. The LTV shock in both cases affects the supply and demand in the rental market, leading to the immediate changes with relatively similar magnitude. However, the rents then interact with rising and declining prices which put different restrictions on the landlords. Increases in prices force new landlords to increase prices to cover higher repayments, whereas decreases in prices leave the changes in rents to the realtors’ valuation and the decay process. Collectively, this leads to asymmetric results in rents.
Conclusion
Understanding the relation between housing market outcomes and the behaviours of its actors is challenging, particularly in variable mortgage rate systems such as the UK housing market. In the context of the UK, considering such cases is timely given the recent financial shocks and their potential spillover effects on housing markets. We have contributed by illustrating a behavioural ABM to explore the consequences of different LTV and interest rate shocks. The ABM code in NetLogo and Python is available at the Github repository https://github.com/YahyaGamal/UK-housing-ABM-version-18.4.2-Public and at https://www.comses.net/codebase-release/b1fa635a-cb84-49c9-a582-0a7f0e7b5207/. These include a version with a simplified user interface for usage in the NetLogoWeb app.
The model is an extension to Gilbert et al. (2009); it explicitly represents the rental and BTL markets while considering the behaviours of landlords, tenants and investors. This makes it useful to understand the spillover effects between rents and housing prices and to explore the effects of financial shocks on households. We demonstrate this through two sets of experiments: one focusing on interest rate shocks and another on LTV shocks.
The interest rate experiments show that a sudden rise in interest rates leads to a decrease in house prices and an increase in rents. House prices decrease until buyers can secure the mortgages required for a purchase. Rents increase as landlords require higher rents to cover higher mortgage repayments. The experiments also show that a sudden decrease in interest rates increases prices and decreases rents. Buyers become able to acquire higher mortgages and this pushes prices upwards. The change in interest rate also affects investors who purchase houses to let, increasing the supply in the rental market. The increase in supply then leads to a reduction in market rents.
The LTV experiments show that prices decrease and rents increase with a sudden decrease in LTV. House prices decrease until the buyers’ capital can cover the deposit required for a mortgage. Rents increase as the investors in the housing market can no longer afford to buy houses, which decreases the supply of houses offered to let. The experiments also highlight that a sudden rise in LTV has the opposite effect. An LTV rise increases housing prices significantly because more buyers become able to afford mortgage deposits — this increases demand and subsequently increases prices. With home buyers being prioritised over investors, the number of houses being purchased by owner-occupiers increases compared to the number of houses offered to let. This creates shortages in the rental market leading to a short period of increase in rents.
The outcomes show that the model is a useful tool for exploring housing market behaviours. However, the ABM comes with a set of limitations embedded in the assumptions made when abstracting the essential features of the housing market. First, the model assumes the mortgage rates are similar for the BTL and owner-occupier housing market (including for first time buyers and investors), yet this is not the case in reality. Second, the model does not simulate leasehold tenures. Third, there is no consideration of the public housing market and the effect of the government’s investment in housing on prices and rents. Finally, the housing transaction procedures occur without a bidding process. This lack of bidding is typical of the English housing market except when the market conditions are changing very quickly — when there can be ‘gazumping’ (making a higher offer for a house than someone whose offer has already been accepted by the seller and thus succeed in purchasing the property).
In future research, we aim to simulate further aspects of the housing market, and to extend the experiments to reflect real events in the UK housing market. We will include geo-spatial factors which will affect households’ selection of houses to buy and rent and realtors’ house valuations. This extension will allow the model to explore the formulation of spatial clusters based on house prices and demographic properties. We also plan to extend the model to include a bidding process when acquiring houses so that we can test the extent to which this contributes to the exclusion of poorer households from the market. For the ABM experiments, we will formulate cases that represent historic events related to changes in LTV and interest rates — for instance, the 2008 financial crisis.
Acknowledgements
The work was made possible by ESRC’s on-going support for the Urban Big Data Centre [ES/L011921/1 and ES/S007105/1].Notes
- In the UK, these are called estate agents, but we have named them realtors to avoid confusion with the agents in the model↩︎
- This observation qualitatively aligns with Gilbert et al. (2009)’s ABM results that show an immediate decrease in prices by 43 percent after increasing interest rates by 3 percent.↩︎
Appendix
In this section, first, we present an extended set of parameters as implemented in the ABM NetLogo code. Second, we clarify in further detail the derivation of Equation 3 shown in the "Model Description" section. Third, we show detailed flowcharts for the scheduling of the model during the initialisation and runs. Fourth, we present the results of a baseline experiment to highlight the market stability process. Fifth, we provide a set of experiments using different grid sizes to justify the selection of a 64x64 grid in the main document. Sixth, we apply a pattern oriented modelling approach to highlight the ability of the model to replicate data-informed patterns and to generate different patterns under variable financial conditions. Seventh, we present the results of a sensitivity analysis for a selected set of input parameters. Finally, we highlight the formulation of spatial neighbourhoods of high and low prices/rents.
Extended ABM parameters
The state parameters shown in Table 1 are relevant for describing the model. Further parameters listed in Table 4 are used in the ABM for technical purposes.
| State variable | Label | Description | Type | ||
|---|---|---|---|---|---|
| Household | myType | type of household (“mortgage" or”rent") | str | ||
| income-rent | income from rent per time step | float | |||
| income-surplus | residual income after spending on housing commodities | float | |||
| mortgage-initial | value of initial mortgage | float | |||
| my-rent | rent to pay at each time step (zero for homeowners) | float | |||
| homeless | count of the number of time steps that this owner has been without a house | int | |||
| made-offer-on | house that this owner wants to buy/rent | house | |||
| date-of-acquire | time step at which my-house was bought/rented | int | |||
| on-market? | currently on the market or not | boolean | |||
| Realtor | my-houses-rent | the houses in the realtor’s territory for rent | list{houses} | ||
| my-houses-sold | the houses in the realtor’s territory for sale | list{houses} | |||
| sales-rent | the last few houses for rent that the realtor has evaluated | list{houses} | |||
| sales-sold | the last few houses for sale that the realtor has evaluated | list{houses} | |||
| House | myType | type of house (“mortgage" or”rent") | str | ||
| local-realtors | the local realtors of the house | list{realtor} | |||
| date-for-sale | last time step at which the house was offered for sale | int | |||
| date-for-rent | last time step at which the house was offered for rent | int | |||
| my-realtor | the realtor evaluating the house if it is offered for sale or rent | realtor | |||
| offered-to | household that has made an offer to buy/rent this house | household | |||
| offer-date | time step at which an offer was made to buy/sell this house | int | |||
| rented-to | the tenant household for this house | household | |||
| rent-date | time step at which the house was rented | int | |||
| G | \(G\) | hot-spot index for this house (see ) | float | ||
| Global | ticksPerYear | the number of time steps simulated per year | int | ||
| density | the housing density in the model space at initialisation | float | |||
| investors | the ratio of households willing to become landlords if they are relatively rich | float | |||
| houseMeanLifetime | the mean number of years before the house is demolished | int | |||
| capitalMortgage | \(\eta\) | the capital to income ratio for mortgage households at initialisation | float | ||
| capitalRent | \(\eta\) | the capital to income ratio for rent households at initialisation | float | ||
| stampDuty? | enforce stamp duty payments or not | boolean | |||
Maximum mortgage calculation
To identify the maximum mortgage a household can cover (Equation 3), we start with an equation for repayment calculation. Kohn (1990) provides Equation 19 which accounts for the decrease of the proportion of the repayments used for interest as the household pays off the core loan over the mortgage period.
| \[ a_i = \frac{I_i.M_i}{1 - (1 + I_i)^{-d.n}}\] | \[(19)\] |
Transforming this formula to have the mortgage \(M_i\) as a function of the repayment \(a_i\) yields the following:
| \[ M_i = \frac{a_i}{I_i}.(1 - (1 + I_i)^{-d.n})\] | \[(20)\] |
Model scheduling
Figures 5 and 6 show detailed flow charts for initialisation and each run step. These flowcharts correspond to the process described in the "Temporality" section in the main document.
Baseline experiment
The results of a baseline experiment are shown in Figure 7. The experiment shows the process of reaching a stable number of houses and the proportions of houses of each type. The proportions are sensitive to: (1) the income of individuals; (2) the Loan To Value ratio (LTV); (3) the interest rate; and (4) propensity threshold to invest in the housing market (see "Sensitvity"). We observe that the proportions have become stable by year 200, which justifies applying the shocks after that time in the experiments — the stability phase is further discussed in the "Sensitvity" section.
Grid size effects
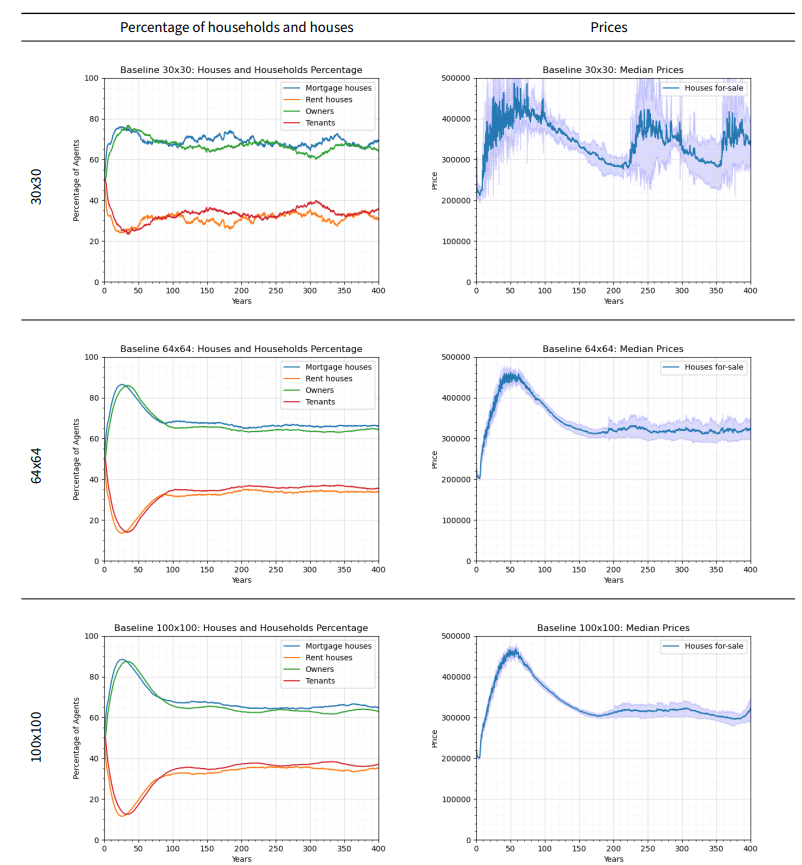
To test the effect of varying the grid size on the model outcomes, we run the baseline experiment on a 30x30, 64x64 and a 100x100 grid. We run each experiment 20 times, and we show the prices of houses and the percentages of houses and households in the system in Figure 8.
Generally, increasing the grid size decreases the fluctuations in the outcomes. In the 30x30 grid, market dynamics lead to proportionately major changes in the number of households in the system and this has a major effect on prices. These in turn create chains of events that lead to waves of peaks and troughs in the ABM outcomes. In case of a financial shock, it becomes challenging to distinguish between the effects of the grid size and the LTV/interest changes. The 64x64 grid results show very minor waves of increase and decrease in prices which are less significant in magnitude compared to changes due to financial shocks. The 100x100 grid results show the least fluctuations in outcomes after the model is stable; however, this comes at a cost in run times. The run times using a laptop with an Intel core i5-1245U processor for a 10 step run are approximately 1.08 seconds, 3.8 seconds, and 38.9 seconds for the 30x30, 64x64 and 100x100 grids respectively. Thus, compared to the 30x30 grid run time, the 100x100 grid takes 31 times as long to run, and the 64x64 grid takes 3.5 times as long. Given this trade-off, we use a 64x64 grid to understand the market dynamics without unacceptable run times.
Outcome patterns under variable financial conditions
We use the Pattern Oriented Modelling (Grimm 1994) approach to validation to test the ability of the model to generate patterns under different conditions reflecting expected trends. As with the main document experiments, we structure the discussion around interest rate shocks and LTV shocks. We start with two data-informed hypotheses and then check to what extent the model outcomes align with the hypotheses under different wage rise, mortgage rate and LTV conditions. We also reflect on the extent to which the simulated patterns align with the results in Gilbert et al. (2009) where relevant.
Interest shock
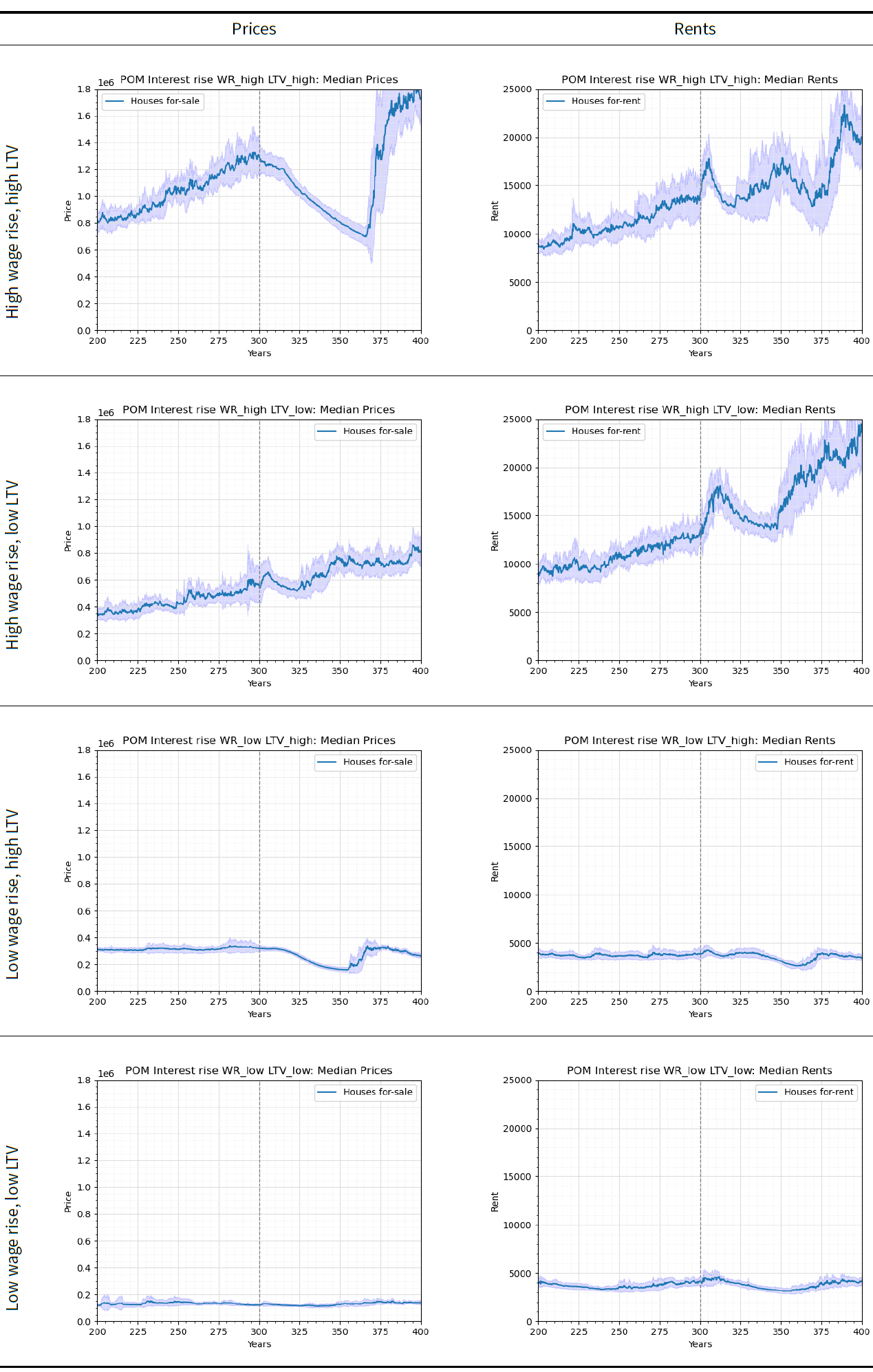
For interest rate shocks, we start with a hypothesis that an interest rate rise should quickly stagnate housing prices and lead to a decrease within one to two years. This is supported empirically with a recorded minor decrease in the UK house prices from September 2022 to September 2023 by 1 percent (Office for National Statistics 2023b), after years of continuous increase. We then run the ABM with an interest rise shock at year 300 under different annual wage rise and LTVs as shown in Table 5 (the other parameters follow the values shown in Table 2 in the main document). The outcomes shown in Figure 9 are then used to check the extent to which the ABM replicates a pattern of immediate decrease in prices.
| Experiment | Parameter | Value |
|---|---|---|
| All experiments | \(I_0\) | 3.7% |
| \(I_{100}\) | 8% | |
| Interest rise (\(I\)) , high wage rise (\(W\)), high LTV (\(L\)) | \(W\) | 0.5% |
| \(L\) | 90% | |
| Interest rise (\(I\)) , high wage rise (\(W\)), low LTV (\(L\)) | \(W\) | 0.5% |
| \(L\) | 60% | |
| Interest rise (\(I\)) , low wage rise (\(W\)), high LTV (\(L\)) | \(W\) | 0% |
| \(L\) | 90% | |
| Interest rise (\(I\)) , low wage rise (\(W\)), low LTV (\(L\)) | \(W\) | 0% |
| \(L\) | 60% | |
The low wage rise and high LTV experiment is the closest to the UK conditions during the recent interest rate increase. In that experiment, the prices decrease immediately after the shock, matching what is observed in reality and in Gilbert et al. (2009)’s ABM — Gilbert et al. (2009) notes that an interest shock from 7 percent to 10 percent decreases prices by 43 percent. Rents also immediately react with an increase which is similar to that currently observed in the UK. A similar trend is also observed in the case of high wage rise, but with a higher magnitude of price drops and a lower magnitude of rise in rent. In contrast, the experiments with low LTVs show an opposite trend for prices where they increase immediately after the shock. However, rents remain unaffected. This shows that the ABM carries further potential to explore different conditions under which financial shocks occur. The experiments can be more strictly informed from real contexts to have a more context-specific understanding of the impact of interest shocks.
LTV shock
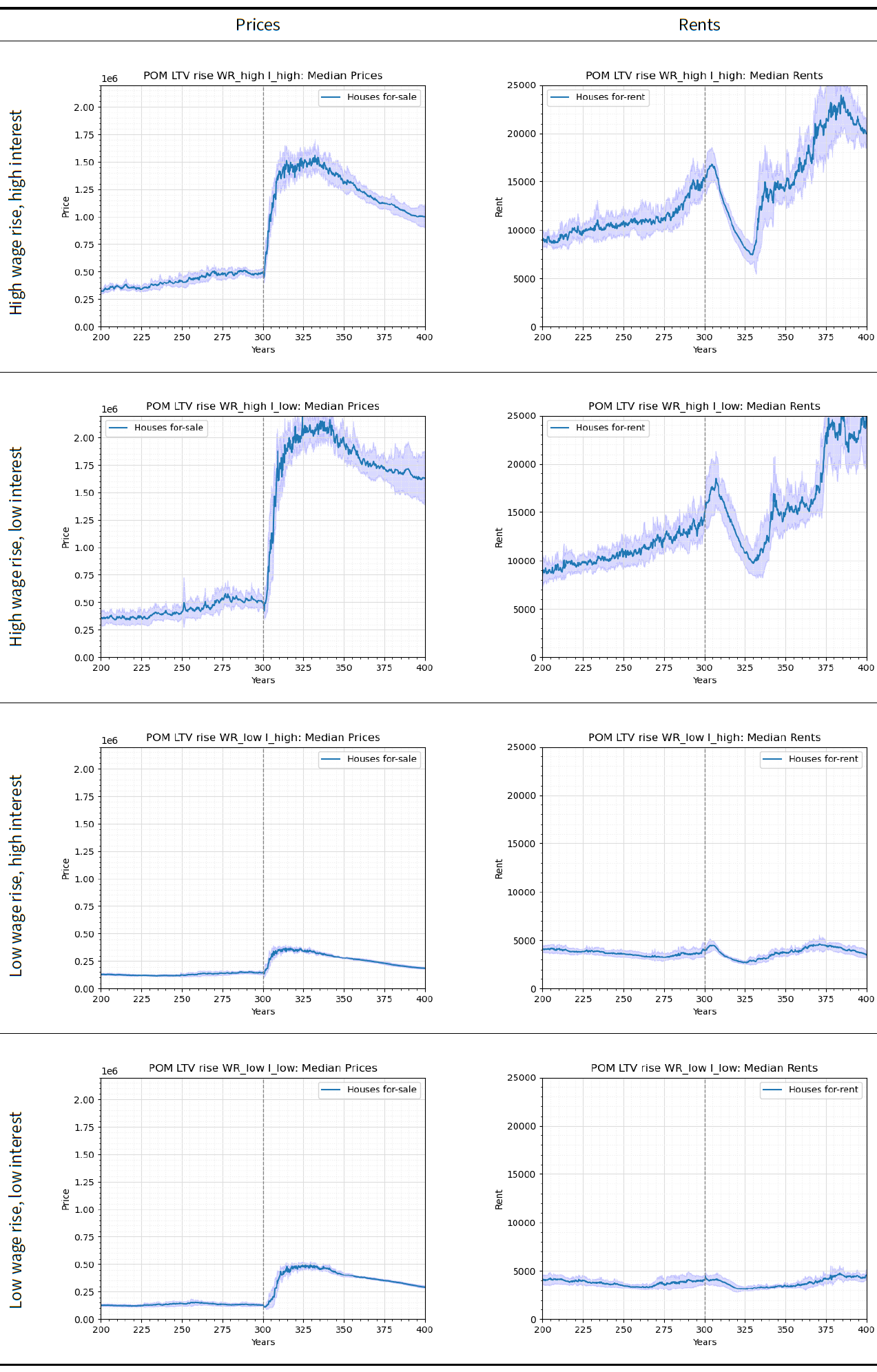
For the LTV shocks, our hypothesis is that an increase in LTV increases housing prices immediately after the shock. Historically, the UK has experienced a gradual increase in prices since April 2012 (Office for National Statistics 2023b) associated with an increase in LTV for first-time-buyers from 75 to 85 percent between 2009 and 2018. We apply an LTV rise shock at year 300 in the ABM runs with different levels of interest rate and annual wage increase as shown in Table 6. The results in Figure 10 are used to check whether the patterns stated in the hypothesis are replicated in the model outcomes.
| Experiment | Parameter | Value |
|---|---|---|
| All experiments | \(L_0\) | 60% |
| \(L_{100}\) | 90% | |
| LTV rise (\(L\)) , high wage rise (\(W\)), high interest (\(I\)) | \(W\) | 0.5% |
| \(I\) | 8% | |
| LTV rise (\(L\)) , high wage rise (\(W\)), low interest (\(I\)) | \(W\) | 0.5% |
| \(I\) | 3.7% | |
| LTV rise (\(L\)) , low wage rise (\(W\)), high interest (\(I\)) | \(W\) | 0% |
| \(I\) | 8% | |
| LTV rise (\(L\)) , low wage rise (\(W\)), low interest (\(I\)) | \(W\) | 0% |
| \(I\) | 3.7% | |
The low wage rise and low interest rate experiment is close to the environment in the UK between 2009 and 2018. Its results show that prices and rents increase after an LTV rise shock. However, this should be approached with caution as the LTV shock is applied suddenly in the runs unlike the gradual LTV increase in the UK. The rest of the experiments show similar trends of prices and rents increasing with different magnitudes. The high wages and high interest rate increase the magnitude of the rise in prices and rents, with wages having more effect on prices and interest rates having a greater effect on rents. This variability in the magnitude of outcomes highlight further potentials of extending the experiments to explore financial shocks in different sets of financial environments.
Sensitivity analysis
We test the sensitivity of the model using a one-parameter-at-a-time approach. We do not aim to provide an exhaustive systematic sensitivity analysis here, rather we show the effect of a set of relevant input parameters for contextualising the ABM. We select four parameter: (A) mean income; (B) interest rate; (C) LTV ratio; and (D) propensity threshold. We use the base experiment to apply a set of runs while varying the values of the input parameter under analysis as shown in Table 7. For each value, the ABM is run 20 times, and the means are calculated at every time step for: (1) median price of houses offered for sale; (2) median rent of houses offered for rent; and (3) percentage of landlords in the population (see Figure 11). Hereafter, we discuss the magnitude of change in the outcomes, and we highlight the waves of increase and decrease during the stability phase — which we label as the ‘periodic stability phase’.
| Input parameter | Values |
|---|---|
| Mean income | {20000, 25000, 30000, 35000} |
| Interest rate | {4, 5, 6, 7} |
| Loan-to-value ratio | {60, 70, 80, 90} |
| Propensity threshold | {0.2, 0.4, 0.6, 0.8} |
Outcome values
The prices are highly sensitive to the mean income, interest rates and LTVs (Figures 11-A1, 11-B1 and 11-C1 respectively). Increasing income or decreasing interest rates allows households to cover higher repayments leading to higher mortgages, which increases prices. Increasing LTV allows households to acquire higher loans with the same capital leading to higher prices. In all cases, the prices change with similar magnitudes across similar increments of change in the input parameters. The propensity to invest only affects the waves of change in the prices. This is later discussed in the "Periodic stability phase" subsection.
The rents are only sensitive to the mean incomes (Figure 11-A2). This is because at initialisation, the rents are set to the maximum the tenants can pay given their income. Hence, higher incomes directly increase rents. In contrast, higher interest rates and lower LTVs do not affect the income of tenants leading to no changes in rents (Figures 11-B2 and 11-C2). It is relevant to note that at different LTV and interest rate initialisations, the repayments are kept lower than the income of owners as previously stated. Hence, landlords do not force increases in rent to cover their repayments. Similar to prices, the propensity to invest only affects the periodic increases and decreases in rents.
The percentage of landlords in the population is highly sensitive to changes in propensity. Propensity thresholds of 0.2 and 0.8 result in approximately 9 percent and 22 percent landlords respectively (Figure 11-D3). This is expected as a propensity of 0.8 implies that 80 percent of the households will make the decision to enter the BTL market when they become relatively rich. LTV changes have less of an effect on the percentage of landlords with its values ranging between 5 percent and 9 percent across all the runs with different LTV values (Figure 11-C3). The percentage of landlords is not sensitive to changes in mean income or interest rate (Figures 11-A3 and 11-B3). This is because the ratio of the investors is sensitive to the time households take to enter the BTL market from initialisation; i.e, the first 50 years of the runs. Changes in LTV significantly decrease the required capital compared to the income of households. This allows households to reach the capital thresholds more quickly and enter the BTL markets. Changes in interest rate keeps the repayments and required capital within the maximum financial ability of households, and it compensates with changing prices at initialisation so that repayments match the incomes. This does not change the required capital for entering the BTL market, and accordingly does not change the percentage of landlords. Increasing mean income increases the accumulation of capital, however it also increases the initial capital of households at initialisation. This implies that the prices are adjusted to require higher capital at higher mean incomes. Hence, the required time for accumulating the required capital remains the same across different input mean incomes.
Periodic stability phase
The periodic stability phase is a state that the ABM enters with repeated waves of increase and decrease in prices with a stable frequency and magnitude. To explain the dynamics of such phase, we start from the first peak observed in a run. At that point, the prices/rents reach the highest value that households on the market can pay leading to decaying prices in the following years. At the next observed trough, the prices/rents become low enough for households to make offers. This decreases the delay effect which allows for higher transaction prices on the market. Higher transaction prices increase the mean prices/rents that realtors consider when valuating houses. Subsequently, higher valuations are made which further increases the mean rents realtors consider. This price/rent increase reinforcement process remains in place until the valuations reach a (second) peak that households can pay. The whole process is then repeated in a way similar to the starting point at the first peak. The magnitude of the fluctuations is directly affected by the changes in the numbers of households in the system and the number of households on the housing markets at each peak. This makes it possible to enter this state after a financial shock has affected the numbers of households on the market as pointed out in the Results section.
The periodic stability phase is highly sensitive to changes in the propensity to invest (Figures 11-D1, 11-D2 and 11-D3). At a propensity threshold of 0.2, the waves in the changes of all the outcomes are minor. These waves become apparent in prices and rents at a propensity threshold of 0.4. Increasing the propensity threshold to 0.6 increases the frequency of the waves, particularly for prices (Figure 11-D1). Beyond that, increasing propensity does not significantly affect the magnitude or frequency of the waves. These observations are explained by the increase in the number of investors in the BTL housing market as a direct result of increasing the propensity thresholds. This reinforces the waves of change in prices as previously discussed, which in turn affects rents.
Otherwise, the periodic stability phase is less sensitive to changes in LTV, interest rates and mean income. Changes in these input parameters affect the starting point of the stability phase, which leads to the occurrence of the waves at different time steps.
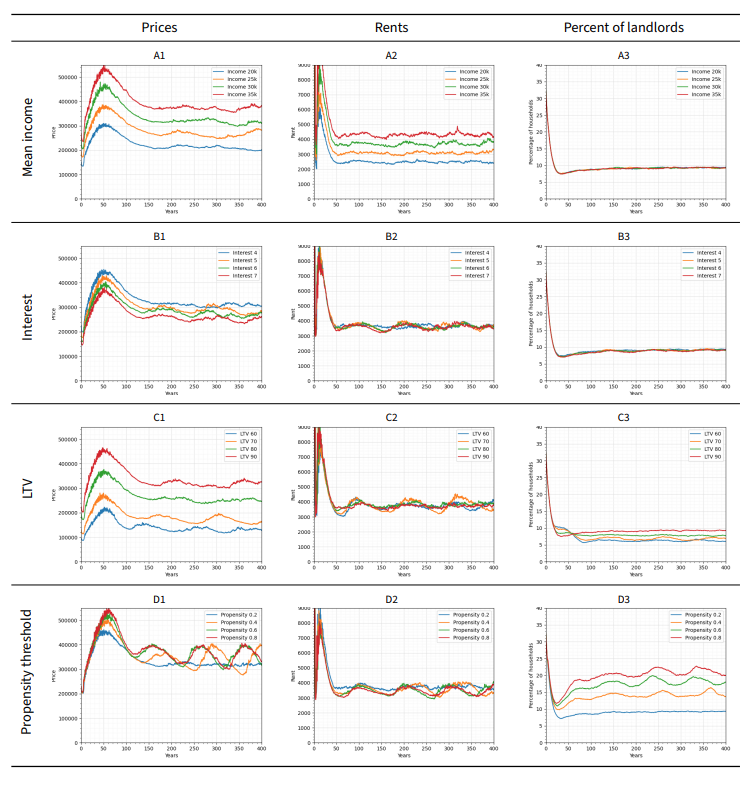
Spatial outcomes
The ABM prices are dictated by realtors with specific spatial locations and a spatial awareness radius. During the runs, areas controlled by specific realtors end up with different price ranges. This drives the formulation of spatial clusters of high prices over the runs presented in the paper. We apply a hot spot analysis comparing the price of each house to: (a) the mean prices of all houses in the system; and (b) the mean prices of spatially proximate houses. This generates a spatial correlation z-value as shown in Equation 21.
| \[ G_j = \begin{cases} \frac{\sum_{j'=1}^m(w_{j'|j}.p_{j'})-\bar{p}_{J_s}.\sum_{j'=1}^m w_{j'|j}} {\sqrt{(\frac{\sum_{j'=1}^mp_{j'}^2}{m} - (\bar{p}_{J_s})^2) . \frac{m.\sum_{j'=1}^m w_{j'|j} - (\sum_{j'=1}^m w_{j'|j})^2}{m-1}}} \text{, } & \text{where } j,j'\in{J_s} \\ \\ \frac{\sum_{j'=1}^n(w_{j'|j}.r_{j'})-\bar{r}_{J_r}.\sum_{j'=1}^n w_{j'|j}} {\sqrt{(\frac{\sum_{j'=1}^nr_{j'}^2}{n} - (\bar{r}_{J_r})^2) . \frac{n.\sum_{j'=1}^n w_{j'|j} - (\sum_{j'=1}^n w_{j'|j})^2}{n-1}}} \text{, } & \text{where } j,j'\in{J_r} \end{cases}\] | \[(21)\] |
We assume that \(w_{j'|j} = \frac{1}{8}\) for the houses in the Moore neighbourhood of \(j\), whereas \(w_{j'|j} = 0\) for all the other houses. A sample spatial analysis for a run of 150 steps with the baseline parameters is shown in Figure 12.
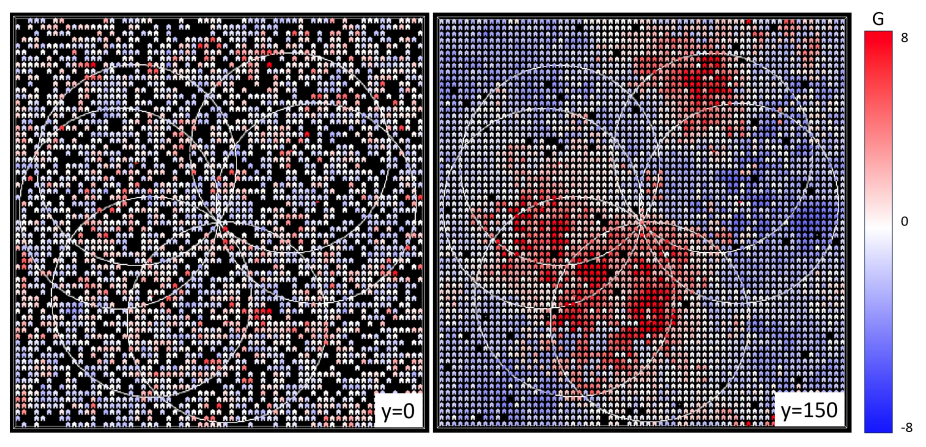
References
AXTELL, R., Farmer, D., Geanakoplos, J., Howitt, P., Carrella, E., Conlee, B., Goldstein, J., Hendrey, M., Kalikman, P., Masad, D., Palmer, N., & Yang, C. Y. (2014). An agent-Based model of the housing market bubble in Metropolitan Washington, D.C. Deutsche Bundesbank Conference - Housing Markets and the Macroeconomy: Challenges for Monetary Policy and Financial Stability [doi:10.2139/ssrn.4710928]
BANK of England. (2020). Why are more borrowers choosing long-term fixed-rate mortgage products? Available at: https://www.bankofengland.co.uk/bank-overground/2020/why-are-more-borrowers-choosing-long-term-fixed-rate-mortgage-products
BANK of England. (2023a). The buy-to-let sector and financial stability. Available at: https://www.bankofengland.co.uk/quarterly-bulletin/2023/2023/the-buy-to-let-sector-and-financial-stability
BANK of England. (2023b). Financial stability report: December 2023. Available at: https://www.bankofengland.co.uk/financial-stability-report/2023/december-2023
BANK of England. (2023c). Quoted interest rates data. Available at: https://www.bankofengland.co.uk/statistics/visual-summaries/quoted-household-interest-rates
BAPTISTA, R., Farmer, J. D., Hinterschweiger, M., Low, K., Tang, D., & Uluc, A. (2016). Macroprudential policy in an agent-based model of the UK housing market. Bank of England working Paper No. 619 [doi:10.2139/ssrn.2850414]
BENHAM and Reeves. (2023). UK’s landlord hotspots revealed – City of London home to the highest number per capita. Available at: https://www.benhams.com/press-release/london-property-market/uks-landlord-hotspots-revealed-city-of-london-highest-per-capita/
BONAKDAR, S. B., & Roos, M. (2023). Dissimilarity effects on house prices: What is the value of similar neighbours? Journal of Economic Interaction and Coordination, 18(1), 59–86. [doi:10.1007/s11403-022-00370-9]
BROWN, D., Page, S., Riolo, R., & Rand, W. (2004). Agent-based and analytical modeling to evaluate the effectiveness of greenbelts. Environmental Modelling & Software, 19(12), 1097–1109. [doi:10.1016/j.envsoft.2003.11.012]
CAMPBELL, J. Y. (2013). Mortgage market design. Review of Finance, 17(1), 1–33.
CARRO, A., Hinterschweiger, M., Uluc, A., & Farmer, J. D. (2023). Heterogeneous effects and spillovers of macroprudential policy in an agent-based model of the UK housing market. Industrial and Corporate Change, 32(2), 386–432. [doi:10.1093/icc/dtac030]
CHOWDHURY, R., & Mosley, M. (2023). Spotlight 1: The impact of rising interest rates on housing costs. Available at: https://www.niesr.ac.uk/wp-content/uploads/2023/08/JC737-NIESR-Outlook-Summer-2023-UK-Spotlight-SA.pdf?ver=mJ0roErpYKisAHYpNPph
CLOYNE, J., Huber, K., Ilzetzki, E., & Kleven, H. (2019). The effect of house prices on household borrowing: A new approach. American Economic Review, 109(6), 2104–2136. [doi:10.1257/aer.20180086]
COKAYNE, G. (2019). The effects of macro-prudential policies on house price cycles in an agent-based model of the Danish housing market. Danmark Nationalbank working paper no. 138
DEPARTMENT of Levelling Up, Housing and Communities. (2023). Dwelling stock estimates, England: 31 march 2022. Available at: https://www.gov.uk/government/statistics/dwelling-stock-estimates-in-england-2022/dwelling-stock-estimates-england-31-march-2022
DILAVER, Ö., & Gilbert, N. (2023). Unpacking a black box: A conceptual anatomy framework for agent-Based social simulation models. Journal of Artificial Societies and Social Simulation, 26(1), 4. [doi:10.18564/jasss.4998]
DLUHC. (2022). English housing survey 2021 to 2022: Household moves - Fact sheet. Department of Levelling Up, Housing and Communities. Available at: https://www.gov.uk/government/statistics/english-housing-survey-2021-to-2022-household-moves-fact-sheet/english-housing-survey-2021-to-2022-household-moves-fact-sheet
EVANS, B. P., Glavatskiy, K., Harré, M. S., & Prokopenko, M. (2021). The impact of social influence in Australian real estate: Market forecasting with a spatial agent-based model. Journal of Economic Interaction and Coordination, 18(1), 5–57. [doi:10.1007/s11403-021-00324-7]
FILATOVA, T., Voinov, A., & van der Veen, A. (2011). Land market mechanisms for preservation of space for coastal ecosystems: An agent-based analysis. Environmental Modelling and Software, 26(2), 179–190. [doi:10.1016/j.envsoft.2010.08.001]
FINANCIAL Conduct Authority. (2024). Mortgages product sales data dashboards. Available at: https://www.fca.org.uk/data/product-sales-data/mortgages-dashboards
GAMAL, Y., Pinto, N., & Iossifova, D. (2023). The role of procedural utility in land market dynamics in Greater Cairo: An agent based model application. Environment and Planning B: Urban Analytics and City Science, 51(4). [doi:10.1177/23998083231207077]
GE, J. (2014). Who creates housing bubbles? An agent-based study. In S. J. Alam & H. V. D. Parunak (Eds.), Multi-agent-based simulation xiv (pp. 143–150). Berlin Heidelberg: Springer. [doi:10.1007/978-3-642-54783-6_10]
GE, J. (2017). Endogenous rise and collapse of housing price: An agent-based model of the housing market. Computers, Environment and Urban Systems, 62, 182–198. [doi:10.1016/j.compenvurbsys.2016.11.005]
GE, J., & Furtado, B. A. (2023). Modelling urban transition with coupled housing and labour markets. Environment and Planning B: Urban Analytics and City Science, 51(3). [doi:10.1177/23998083231186623]
GEANAKOPLOS, J., Axtell, R., Farmer, J. D., Howitt, P., Conlee, B., Goldstein, J., Hendrey, M., Palmer, N. M., & Yang, C. Y. (2012). Getting at systemic risk via an agent-based model of the housing market. American Economic Review, 102(3), 53–58. [doi:10.1257/aer.102.3.53]
GILBERT, N., Hawksworth, J. C., & Swinney, P. A. (2009). An agent-Based model of the English housing market. Technosocial Predictive Analytics Association for the Advancement of Artificial Intelligence Spring Symposium Technical Report SS-09-09
GRIMM, V. (1994). Mathematical models and understanding in ecology. Ecological Modelling, 75–76, 641–651. [doi:10.1016/0304-3800(94)90056-6]
HARRÉ, M. S., Eremenko, A., Glavatskiy, K., Hopmere, M., Pinheiro, L., Watson, S., & Crawford, L. (2021). Complexity economics in a time of crisis: Heterogeneous agents, interconnections, and contagion. Systems, 9(4).
HELLEBRANDT, T., Young, G., & Waldron, M. (2008). The financial position of British households: Evidence from the 2008 NMG Research survey. 2008 NMG Research survey
HUANG, Q., Parker, D. C., Sun, S., & Filatova, T. (2013). Effects of agent heterogeneity in the presence of a land-market: A systematic test in an agent-based laboratory. Computers, Environment and Urban Systems, 41, 188–203. [doi:10.1016/j.compenvurbsys.2013.06.004]
JIANG, N., Crooks, A., Wang, W., & Xie, Y. (2021). Simulating urban shrinkage in Detroit via agent-based modeling. Sustainability, 13(4), 1–22. [doi:10.3390/su13042283]
KOHN, R. E. (1990). A capital budgeting model of the supply and demand for loanable funds. Journal of Macroeconomics, 12(3), 427–436. [doi:10.1016/0164-0704(90)90006-v]
KORN, R., & Yilmaz, B. (2022). House prices as a result of trading activities: A patient trader model. Computational Economics, 60(1), 281–303. [doi:10.1007/s10614-021-10149-y]
LALIOTIS, D., Buesa, A., Leber, M., & Población, J. (2020). An agent-based model for the assessment of LTV caps. Quantitative Finance, 20(10), 1721–1748. [doi:10.1080/14697688.2020.1733058]
LEA, M. (2010). International comparison of mortgage product offerings. Research Institute for Housing America
LIGMANN-ZIELINSKA, A. (2009). The impact of risk-Taking attitudes on a land use pattern: An agent-Based model of residential development. Journal of Land Use Science, 4(4), 215–232. [doi:10.1080/17474230903220386]
MAGLIOCCA, N. R., & Walls, M. (2018). The role of subjective risk perceptions in shaping coastal development dynamics. Computers, Environment and Urban Systems, 71, 1–13. [doi:10.1016/j.compenvurbsys.2018.03.009]
MÉRŐ, B., Borsos, A., Hosszú, Z., Oláh, Z., & Vágó, N. (2023). A high-resolution, data-driven agent-based model of the housing market. Journal of Economic Dynamics and Control, 155.
MORTGAGES for Business. (2020). Distribution of buy-to-let mortgages by term preferences. Available at: https://www.statista.com/statistics/1121084/distribution-of-buy-to-let-mortgages-by-term-preferences/
OFFICE for National Statistics. (2023a). Employee earnings in the UK: 2023. Available at: https://www.ons.gov.uk/employmentandlabourmarket/peopleinwork/earningsandworkinghours/
OFFICE for National Statistics. (2023b). UK house price index: September 2023. Available at: https://www.ons.gov.uk/economy/inflationandpriceindices/bulletins/housepriceindex/september2023
OFFICE for National Statistics. (2024a). Average weekly earnings in Great Britain: April 2024. Available at: https://www.ons.gov.uk/employmentandlabourmarket/peopleinwork/employmentandemployeetypes/.
OFFICE for National Statistics. (2024b). Population estimates for the UK, England, Wales, Scotland, and Northern Ireland: Mid-2022. Available at: https://www.ons.gov.uk/peoplepopulationandcommunity/populationandmigration/populationestimates/
OZEL, B., Nathanael, R. C., Raberto, M., Teglio, A., & Cincotti, S. (2019). Macroeconomic implications of mortgage loan requirements: An agent-based approach. Journal of Economic Interaction and Coordination, 14(1), 7–46. [doi:10.1007/s11403-019-00238-5]
PANGALLO, M., Nadal, J. P., & Vignes, A. (2019). Residential income segregation: A behavioral model of the housing market. Journal of Economic Behavior and Organization, 159, 15–35. [doi:10.1016/j.jebo.2019.01.010]
PARKER, D. C., Brown, D. G., Filatova, T., Riolo, R., Robinson, D. T., & Sun, S. (2012). Do land markets matter? A modeling ontology and experimental design to test the effects of land markets for an agent-Based model of ex-Urban residential land-Use change. In A. J. Heppenstall, A. T. Crooks, L. M. See, & M. Batty (Eds.), Agent-Based Models of Geographical Systems (pp. 525–542). Dordrecht: Springer Netherlands. [doi:10.1007/978-90-481-8927-4_26]
PRUNETTI, D., Dettoto, C., Idda, C., Innocenti, E., Ling, Y., & Vinciguerra, C. M. (2021). ABM/LUCC of a complex economic system of land and home markets facing an intense residential development. 2021 IEEE Symposium Series on Computational Intelligence, SSCI 2021 - Proceedings [doi:10.1109/ssci50451.2021.9660189]
STATISTA. (2024). Median loan-to-value (LTV) ratio for mortgage sales in the United Kingdom (UK) from 2016 to 2023. Available at: https://www.statista.com/statistics/1077616/median-loan-to-value-ratio-for-mortgage-sales-in-the-united-kingdom/
TARNE, R., Bezemer, D., & Theobald, T. (2022). The effect of borrower-specific loan-to-value policies on household debt, wealth inequality and consumption volatility: An agent-based analysis. Journal of Economic Dynamics and Control, 144. [doi:10.1016/j.jedc.2022.104526]
UK Finance. (2019). The changing shape of the UK mortgage market: Emerging themes. Available at: https://www.ukfinance.org.uk/system/files/The-changing-shape-of-the-UK-mortgage-market-FINAL-ONLINE-Jan-2020.pdf
WILENSKY, U. (1999). NetLogo. Northwest University, Center for Connected Learning and Computer-Based Modeling (CCL). Available at: http://ccl.northwestern.edu/netlogo/
ZHUGE, C., & Shao, C. (2018). Agent-based modelling of purchasing, renting and investing behaviour in dynamic housing markets. Journal of Computational Science, 27, 130–146. [doi:10.1016/j.jocs.2018.05.007]