This paper presents an agent-based simulation model of protest activity. Agents are located in a two dimensional grid and have limited ability to observe the behavior of other agents in the grid. The model is used to explore questions inspired by research on different theories of individual motivation and the so-called theory of critical mass. The simulations describe individuals who support an effort to change a policy, but acting in support of that effort is costly. When the marginal effect of participation reaches a certain level, people are more likely to get involved. With certain configurations of parameter values, the simulations produce no sustained widespread participation in protest regardless of the presence of activists; under other conditions high levels of protest are usually sustained, even without activists. However, the addition of a surprisingly small group of activists radically changes the aggregate behavior of the model under some conditions, making high and sustained protest possible when it otherwise would not have been.

Keywords:

Critical Mass; Protest; Simulation; Social Movements; Swarm

"Only a few were our people; the rest just seemed to come from nowhere. You could tell by the way they acted that it was all new to them. They sure weren't hard-core demonstrators" (Agapito Aquino, quoted in Johnson 1987, 83).

Introduction

1.1

On the night of February 22, 1986, Agapito Aquino, brother of slain Philippine opposition leader Benigno Aquino, and Jaime Sin, archbishop of Manila, broadcast calls over Manila's Catholic radio station asking for volunteers. They wanted citizens to march to Camp Aguinaldo, and there to form a human wall of defense, protecting Defense Minister Juan Ponce Enrile and his group of rebels from the Philippine military.

1.2

At 11:00 p.m. Aquino waited at the arranged meeting point with a group of six followers. People began to arrive at 11:15. It took fifteen minutes for the group to grow from 200 to 2000; by 11:45 it was 10,000 strong, and 15,000 marched to the camp shortly after midnight (Johnson 1987).

1.3

The group was not devoid of activists; Aquino was a leader of several demonstration groups and Sin deployed Manila's legions of nuns. These nuns and veteran demonstrators formed the core of what became a four-day series of street protests that involved millions of people and helped to overthrow one of the world's most durable regimes. But the vast majority of people involved were ordinary citizens who belonged to no organization at all. Further, so far as we know, they did not receive any personal incentive in return for participating.

1.4

In this paper, we attempt to ascertain the conditions under which protest actions of that sort can develop. We begin with a discussion of the literature on protest. To explore our ideas, we create a computer simulation model of individual beliefs and behaviors. The results indicate that, under certain settings of the parameters, a small group of agents whose only resource is commitment, or the propensity to protest and keep protesting, can lead by example, producing a large and sustained protest in which most participants are not members of the original group. In our simulation, the conditions that make this possible are those that pertained in Manila in 1986: sufficient population density and communications to enable each person to observe the behavior of a fairly large group of others, and relatively high resistance by the regime to the protesters' demands.

Framing the Problem

2.1

One of the most significant problems for theoretical and empirical research into social protest and revolution is the collective action problem (Olson 1965). Protest movements face a free-rider problem. Even though all members of a society might want to get rid of their government, or significantly change it in some way, the Olsonian logic seems to predict that nothing will happen, unless a leader appears who can offer people something selective in return for participating. Gordon Tullock was one of the first political economists to extend this logic to its fullest: "The public good aspects of a revolution are of relatively little importance in the decision to participate" (Tullock 1971, p. 92). Instead, Tullock contended that the effort to obtain private goods--a personal share of the benefits of political change--was the prime motivation.

2.2

Many scholars have been reluctant to accept this explanation for the willingness of individuals to participate. Some of the reluctance is based on empirical grounds (Muller and Opp 1986). Partly because of the empirical shortcomings of the private goods explanation for protest, other theorists have proposed models that emphasize a social ``success motivation'' that individuals might hold. The success motivation theories claim that people act because they think their participation will have an impact on the end result (Fireman and Gamson, 1979; Finkel, Muller, Opp 1989; Obershall 1980). Oberschall contends that the probability of success in a protest movement has an S-shaped curve which depends on the number of protesters (1980). When the number of participants is either very small or very large, the individual impact is small because the collective effort is very likely either to fail or to succeed without an additional contributor. In the middle ranges, however, individuals think the chances that they will tip the scale are higher and they are therefore more likely to participate.

2.3

Marwell and Oliver pursued this notion in a series of studies using computer simulation. They advanced the ``theory of the critical mass.'' Their fundamental assumption was that the collective action problem could be overcome if (1) individual impact is rising in some portion of the ``production function'' and (2) a ``critical mass'' of highly resourceful and interested individuals exists whose contributions push the collectivity into the ``right part'' of the curve, thus making it profitable for others to join. The ``critical mass'' studies explored the effects of different production functions, interest and resource heterogeneity (Oliver, Marwell and Teixeira 1985), group size (Oliver and Marwell 1988), characteristics of social networks (Marwell, Oliver, and Prahl 1988), selection strategies (Prahl, Marwell and Oliver 1991), cliques (Marwell and Oliver 1991), and all of the above (Marwell and Oliver 1993).

2.4

The theory of the S-shaped curve implies that protest can occur if the dynamical sequence of events is ``just right.'' This is one of the major points in the theory proposed by Timur Kuran. Kuran proposes a threshold model (Granovetter 1973; Schelling 1978) of preference revelation, one in which people reveal their disapproval of a regime only when they believe that a sufficiently high percentage of other people in the society also disapprove (Kuran 1989, 1991, 1995). One of Kuran's contentions with which we agree strongly is that objective social conditions can set the stage for protests to arise, but they do not in any substantial way help us to understand when and how discontent is eventually manifested. Rather, discontent is eventually manifested through a complicated chain of individual interactions which cannot be predicted with a high degree of precision.

2.5

Kuran leaves open several questions for analysis. First, there is the problem of limited information. Kuran contends, quite rightly, that an unpopular political regime ``has an incentive to discourage independent polling and discredit surveys that reveal unflattering information'' (1991, p. 21). However, in his formal analysis, Kuran proceeds to propose a protest model in which citizens have complete information about the views expressed by others. We propose to develop an alternative perspective, one in which individuals are only able to perceive the discontent expressed by others within a well-demarcated field of vision (neighborhood). It is interesting to ask whether this new assumption that agents are ``myopic'' will significantly change the prediction of the model. Second, through a computer analysis, we want to offer some insights into the conditions into which a ``prairie fire'' of discontent can be started and propagated. Like Kuran, we believe that protests can be triggered by the introduction of a relatively small number of activists who behave differently. This is a person for whom the cost of ``dissent may be outweighed by the satisfaction he derives from being true to himself'' (1991, p. 19). The computer model yields some new insights into the dynamics of the process.

2.6

There is an alternative explanation of protests based on ``information cascades.'' Most notable is Lohmann's (1994) study of political upheaval in East Germany between 1989 and 1991. The information cascade model claims that citizens are unsure whether their government is bad or not. As they observe discontent, they increasingly think that their political regime is undesirable. The details of the East German case are not our main point of interest, but we have some serious doubts about the empirical relevance of that account. Our model supports an alternative treatment offered by Przeworski (1991). The collapse of the East European regimes was not caused by the diffusion of information about the unattractiveness of the regimes; many people already thought the regimes were bad. What diffused was information about the probability that the regime would give in. People were "updating their probabilities of success" (Prezworski 1991, pp. 3-4). The information cascade model, like Kuran's threshold model, presupposes that people can observe the behavior of all other people in coordinating their actions. Our model of behavior with myopic agents is, of course, based on quite a different view of the situation.

2.7

The model we present has a number of novel features. We implement an agent-based model in which individual behavior inherits the S-shape of the ``success motivated'' models. We explore the impact of limited information about the behavior of other people. We explore the background possibilities of success-motivated protest, and then explain the conditions under which the addition of a small group of dedicated activists who lead only by example can make a difference. In our emphasis on heterogeneity in an agent-based framework, the research strategy has an element in common with other recent projects on social construction (Lustick 2000; Lustick and Miodownik 2000).

2.8

While the implications of the model are rich and point in many directions for future study, the most important points are the following. First, because success-motivated protest occurs when individuals perceive the probability of success as being in its mid-range, all parameters that affect it have nonlinear and interactive effects. Second, the introduction of heterogeneity in the types of agents--including some agents who protest consistently regardless of the behavior of others--can have a dramatic impact on the level of collective action observed. Sometimes, when a society of discontented people exhibits no tendency to express its discontent, the addition of a few consistently active individuals can lead to widespread protest.

An Agent-Based Simulation Model

3.1

One strength of the agent-based modeling approach is that one can consider rich, empirically meaningful theories of individuals as well as various conditions under which they might interact. Nevertheless, to preserve some theoretical clarity, we pitch the model at a rather abstract level. The agents are located in two-dimensional space that might roughly be thought of as the map of a city or state. We have typically considered models that are represented by a 40-by-40 grid of cells. In this report, we allow the grid to ``wrap around'' to form a torus (as a result, no agent is ``on the outside edge'' of the world). The model diverges from a typical cellular automata model in one vitally important way. Although each cell of the grid has eight neighboring cells, each cell can hold any number of agents, or it might hold none at all.

3.2

In our model, time passes in discrete steps. At each iteration, each agent has the opportunity to join or withdraw from a collective protest action. To avoid peculiar effects due to repetition of the model, we have taken two modeling strategies. First, the order in which agents act is randomly shuffled after each iteration. Second, each agent's action is registered in the environment immediately. (That is to say, the models we describe here are all asynchronous in nature). The code for the model is freely available under the terms of the GNU Greater Public License. The computer model was written in Objective-C using libraries from the Swarm Simulation System version 2.1.1. It is available at http://lark.cc.ukans.edu/~pauljohn/Swarm/MySwarmCode/activists-20020412.tar.gz

3.3

An agent's behaviors consist of observing all the cells within a specified radius in order to measure the proportion of other agents that are contributing to a collective action, and then contributing (or not). Each agent performs both of its behaviors before the next agent, rather than all agents looking, then all agents acting.

The Agents' Beliefs and Propensities

3.4

Activists are agents who will protest no matter what happens. Their propensities are quite simple as a result.

3.5

The ordinary citizens, however, are a bit more interesting. Our plan is to focus on the impact of individual perceptions and interdependence without imposing too many distracting ad hoc assumptions. In this pursuit, we are adhering to the kiss principle (``keep it simple, stupid!'' Axelrod 1997, p.5). The intention is to lay bare the assumptions and implications of the ``success motivation'' theories. Our objective is to understand enough about political upheaval in the world of ordinary agents and then to appreciate the introduction of activists at a later stage.

3.6

Suppose that all of these ordinary agents desire the same goal and all are motivated by the desire to help the movement succeed. As proposed by Oberschall (1980), they believe that the probability of success is an S-shaped curve, which we have represented by the logistic relationship:

Probability  of  success=

1 1+e(a-bX)

(1)

or, equivalently,

Probability  of  success=

1 1+e-(-a+bX)

(2)

We assume that b>0, indicating that the proportion of agents who are participating (X), has a positive effect on the probability of success. The effect of adding a protester is maximized when the proportion of agents protesting is a/b, so the constraint that 0 < a/b < 1 assures that the maximum does not exist at either extreme. This assures that the curve is thus S-shaped.

3.7

The spatial element of the simulation arises because we believe that, during times of political upheaval, people don't typically have comprehensive information about the state of the political situation. Rather, they can observe the behavior of people within a limited neighborhood of their personal experience. In this project, we explore the implications of the idea that agents project from their local observations to formulate expectations about the larger political framework. The agent lacks the information to make the calculations described in Equation 1 with perfect accuracy; its information is strictly local. The agent does not know how many agents are currently protesting throughout the society, but rather has knowledge only of people within a given radius of vision. The agent is able to gauge the proportion of others who are taking action within that radius.

3.8

We proceed with the hypothesis that each agent assumes that its locality is typical. In doing so, the agent estimates the probability of successful collective action as described in Equation 1, except that the proportion of visible agents protesting (x) is put in place of the aggregate proportion protesting (X).

3.9

Since each agent is motivated solely by the desire to help the movement succeed, the agent's probability of protesting is the greatest in the mid-ranges of this relationship, where the individual's marginal impact is the greatest. This implies that the probability of individual participation, P_i(x) , is proportional to the slope of the relationship that the individual perceives between the level of protest and the probability of success:

	(3)

In the simulation models described below, we suppose there is a constant of proportionality, k , such that

	(4)

The constant of proportionality k is constrained to assure that P_i(x)<1 , making this model of individual behavior probabilistic.

  Parameters of the ordinary success-motivated agent

3.10

The grid on which the agents are randomly arranged is 40-by-40. As we explore the model of ordinary success-motivated agents, we can adjust the population level (the number of agents distributed over the 1600 cells), the vision radius of the agents (which determines the number of cells in all directions that are taken into account by the agent), as well as the parameters which govern the response of the political regime, a and b , and the constant of proportionality, k.

3.11

The parameter a is a ``nuisance'' parameter, in the sense that none of our results hinge on its particular value. That parameter determines the probability that the political regime will give the protesters what they want, even if no level of protest action manifests itself. That is to say, even if the level of participation is 0, there is still a possibility, however small, that the goal desired by the agents will be achieved. The probability of that occurring is 1/1+e^a . In all of the experiments recorded here, we held a constant at 8, implying that agents believe the probability of success when no one visible is protesting is 0.0003.

3.11

The responsiveness or resistance of the political regime is one of the parameters in which we are interested. The parameter, b, is important because it determines how rapidly the probability of success responds to changes in protest participation. In particular, we have focused on the idea of ``regime resistance,'' which is represented by the ratio a/b. If the level of protest equals a/b, then the probability of success is 0.5, and the impact of adding an additional protester is at its maximum. If a/b is a very small number, the political system is acutely responsive, while if the number is higher, it means that the regime ignores protest until it rises to a higher level. Our experiments used values of 1/20, 1/14, 1/8, and 1/2. The individual's effort makes the most difference for success at this protest level, and thus it is here that each agent's likelihood of protesting is at its maximum.

3.12

We adjusted the free parameter k so that the maximum probabilities of protesting remained the same in all experiments. For each value of a/b, k was set so that the maximum probability of protesting for any agent at any time would be 0.99. The agent's probability of protesting when there are no visible protesters was the same across all experiments: it is 0.0013.

Summary of the Model Design

3.13

The code for this model is freely available and we encourage readers to inspect it. The sequence of events in the model is orchestrated as follows.

1. The regime resistance coefficient is set at a constant value.
2. A sample of N agents is created and assigned at random (uniform distribution) to positions in the grid.
3. At each time step, the following occurs:

• The list of agents is shuffled.
• Each agent measures protest within its vision radius, calculates the proportion of people who are protesting, and decides whether to protest (see 4).
• Each agent's behavior is immediately registered in the environment of all succeeding agents.

In the model we report here, the agents never move about in the grid and new agents are never created after the simulation has begun.

Results

The Behavior of Ordinary Agents

4.1

We have observed may interesting patterns while exploring the behavior of agents in this model. At its core, the success-motivation has a confounding sort of nonlinearity: agents will not join if it is ``too hot'' or ``too cold,'' but rather ``just right'' (with apologies to Goldilocks). Because agents are most likely to protest when they believe they will make a difference, the probability of success cannot be too high or too low, or they will refuse to act. Vision radius and population both determine the number of others an agent can see. If an agent can see too few others, then even a small number of visible protesters has an inordinate effect on the agent's visible proportion protesting and thus on the perceived probability of success, moving it far above the range of highest protest propensity for the agent. If the agent sees too many others, one or two protesters are too small a proportion of the visible total to bring the probability of success up into its mid-range, and again the agent is reluctant to contribute.

4.2

Because the aggregate patterns of protest depend on a complicated interplay of individual perceptions and social behaviors, a great deal of variety is observed across a set of simulations. In many runs of the model, ``nothing happens.'' There are small seeds of social action, but nothing beyond random individual expressions of discontent. In other runs, however, it is apparent that there are quite complicated dynamics, as a protest movement grows rapidly. The results are difficult to summarize neatly, but we have settled on the strategy of running the model for 1000 iterations and then calculating the summary statistics, such as mean and maximum levels of protest observed across that time period.

4.3

Regime resistance values tested were 1/20, 1/14, 1/8, and 1/2. Variations in two other parameters were considered as well. We used different population sizes ranging from 200 to 1000 by increments of 200. And while we gave all agents in any single experiment the same vision radius, we experimented with seven different radii ranging from one to seven by increments of one. Thus in some experiments agents were very myopic, seeing only nine of the 1600 cells on the grid; in others they were fairly far-sighted and capable of seeing 225 cells, with the remainder of experiments in between the two extremes. There are 140 combinations of these parameter values, and we started our investigations by running five experiments with different random seeds at each configuration, creating a total of 700 experiments. Each experiment lasted for 1000 iterations.

4.4

In order to convey the relationship between the parameters and the outcomes of the simulations, we begin with a meta analysis of the results. Table 1 shows ordinary least squares regression results for a model in which the dependent variable is the mean protest level during a 1000-iteration experiment and the independent variables are these parameters and interactions among them. Population, vision radius, and regime resistance all have positive effects on the level of protest if those parameters are set at small values, while the signs of the squared terms indicate that the effect diminishes and then turns negative.

Table 1: Effects of Regime Resistance (a/b), Population, and Vision on Mean Protest Level

Variable	OLS estimate	t-stat
a/b	161.799	17.829
Population	0.027	8.478
Vision Radius	9.593	22.229
(a/b) Squared	-250.362	-17.926
Population Squared	-0.00000606	-2.682
Vision Radius Squared	-0.661	-15.132
(a/b)*Population	-0.039	-5.951
(a/b)*Vision Radius	-8.537	-8.806
Population * Vision Radius	-0.004	-10.378
(a/b)*Population * Vision Radius	0.007	4.885
Constant	-27.254	-18.195
R2	.71
N	700

4.5

The complicated and nonlinear logic of success-motivated protest is seen plainly in the effect of the regime resistance parameter. Regime resistance has an effect similar to population and vision. If the parameter b is very small, then no amount of protest will matter, and people don't join, since the regime is highly resistant to the forces of change. As b is increased, then resistance (a/b) goes down, and the willingness to join rises. However, once resistance drops to a certain level, then only a small number will ever protest. When the agents perceive that even a small percent protesting might succeed, then many agents will not join the effort. On the other hand, if regime resistance is too high, the agent perceives success as too remote, even if he or she sees some others protesting.

4.6

Predictably, the effects of population level (which determines density) and the agent's vision radius (which is, in effect, perceived density) interact with one another. Suppose agents can see only a few other agents. Then a single act of protest will convince all agents within vision that the level of protest, as a proportion of citizens, is high. If regime resistance is low, others do not protest because they think that their contribution would be unnecessary. Adding additional agents, however, causes the density of local environments to rise. A single agent's expression of discontent is not enough to convince the others that the regime will respond favorably without their additional contribution. In this middle range of population, then, we have the possibility that protest can spread by drawing new participants who believe they are making a difference. When the population becomes extremely dense, however, then individual agents again conclude that their personal contribution would be insufficient to affect the regime.

4.7

In the following sections, we restrict our attention to a setting in which the agents are limited in their vision. However, we have conducted simulations in which the agents have a full vision of the grid. For example, suppose each agent has a vision radius of 19. If there are no activists, and the population in the grid exceeds 2000, then the average level of protest observed is never greater than one percent. That is to say, the protest observed reflects the occasional individual outburst, but no self-sustaining pattern of protest develops. At the lowest level of regime resistance, 1/20, then, a densely populated society of agents with high vision radius is not likely to exhibit much protest.

4.8

From these simulations, we have formulated some opinions about the conditions under which the addition of a few activists ought to make a difference. Since the presence of activists can only increase but not decrease the other agents' estimates of the probability of success, activists should help to promote protest only when the perceived probability of success is too low. This happens when agents can see too many other agents or when the regime is too resistant to protester demands. We would not expect activists to make a difference when the population or vision radius is low, or when the regime is prone to giving the protesters what they want.

Just a few activists can have a major impact, if conditions are right.

4.9

To verify the reasoning above we create a new type of agent, the activist, that protests during every iteration. The activist is otherwise identical to the other agents, meaning that it can influence others only by example, not by reward or punishment. We experimented with a number of models, but we found some of the most interesting results when just a few activists were introduced as a tightly concentrated group, so we placed them all in the same cell in the center of the grid. To begin, we ran 700 new experiments with the same parameter values as in our original simulations, but now with ten activists in the center cell. Then we repeated these experiments with twenty activists, giving us a total of 2100 experiments to compare, including the original set. For ease of presentation, we held population constant at 600 to create Table 2, which shows the difference that twenty activists make at each level of vision and regime responsiveness.

Table 2: Means of Average Protest Level During Each Experiment

			Vision
Regime Resistance	N. of Activists		1	2	3	4	5	6	7
1/2	0		0.9	0.0	0.0	0.0	0.0	0.0	0.0
1/2	20		0.8	00.1	01.0	02.7	05.1	17.8	01.5
1/8	0		0.2	18.2	19.6	19.9	19.7	18.1	3.8
1/8	20		0.2	18.1	19.2	19.3	19.1	16.2	16.0
1/14	0		0.0	4.9	14.1	13.4	13.6	13.5	13.6
1/14	20		0.0	4.6	13.8	13.0	13.0	12.7	13.0
1/20	0		0.0	0.1	10.8	10.1	10.5	10.4	10.9
1/20	20		0.0	0.0	11.0	9.9	10.2	09.9	10.0

Entries are means of average protest levels observed across 5 experiments, each of which lasted 1000 iterations. Population is fixed at 600. Regime resistance is a/b, the protest level that makes probability of success = 0.5.

4.10

As expected, activists make a difference when the regime is highly resistant to protester demands and when vision radius is high, in the upper right cells of the table. At these values the agents think the probability of success is too low, and a few activists can raise it into the region where they think their own effort will be worthwhile. However, activists do seem to be more effective at vision radius 6 than 7, provided regime resistance is very high. This indicates that their ability to overcome perceptions of a low probability of success is somewhat limited as well.

Illustration of the impact of activists.

4.11

To better illustrate the dynamics of a model with some activists, we present a comparison of the graphs of protest growth and snapshots of the grids from several runs of the model. During our research, we conducted many simulations with varying population, regime resistance, and vision radius. For illustration purposes, we have selected a series of runs of the model in which the population is 688, regime resistance is 1/20, and the vision radius of the agents is 6. Figure 1a shows the graph of protest growth during 1000 iterations of that model when there are no activists. Figure 1b is a snapshot of the grid during iteration 269 of the same experiment. 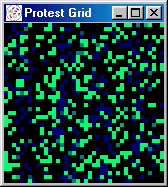It is color coded so that black cells are empty, dark blue represents an occupied cell with low protest, and bright green indicates high protest levels.

---

Figure 1: Low Regime Resistance (a/b = 1/20 )

[ Protest Levels]

[Grid Snapshot]

---

4.12

The low regime resistance in Figure 1 produces a saturation effect; even a small amount of visible protest is sufficient to make agents believe that the probability of success is too high to make their contribution worthwhile. The result is small clusters of protest distributed fairly evenly across the grid.

---

Figure 2: Effect of Activists with Low Regime Resistance (a/b = 1/20 )

[Protest Level]

[Grid Snapshot]

---

4.13

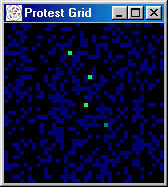
The snapshot in Figure 1 is not atypical; the individual protesters change constantly, but the general pattern does not. If we add activists into a world with a very responsive government, the impact is not too great. Figure 2 illustrates what happens when we run the same experiment again, but this time with 20 activists added to the center cell. (Again, the picture of the grid in panel b was taken on iteration 269, a representative iteration.) The activists make almost no difference. Protest does not grow because the regime is too responsive to the protesters' wishes and the probability of success rises too quickly in response to protest; adding activists actually exacerbates this problem slightly. Individuals who might join and pitch in are discouraged because only a small amount of collective effort is needed and because others appear willing to provide it. The region around the center cell in panel b has lower protest than it otherwise would, because agents there have no interest in helping a cause that seems almost sure to succeed anyway.

---

Figure 3: High Regime Resistance (a/b = 1/2)

[Protest Levels]

[Grid Snapshot]

---

4.14

Activists are more likely to make a difference if the regime's resistance to the protesters' demands is increased. Figure 3 illustrates a sample run in which there are no activists and regime resistance is increased to 1/2. There is almost no protest activity at all. There are occasional individual agents who randomly express their opinions, but they are not sufficient in number to persuade others to join up. The protest seems a lost cause.

4.15

When regime resistance is high, adding a few activists can make a big difference because activists raise the probability of success significantly in their neighborhood, and the new, more hopeful estimation spreads. In Figure 4, we present a graph which shows the level of protest rises in a way that is indicative of contagion. This model is the same as the one represented in 3, but it introduces 20 activists in the center cell. For 240 iterations the presence of the activists has almost no effect. Then (apparently at random) protest begins to spread, growing in spurts to 60 percent. Figures 5 and  6 present a series of snapshots of the protest grid during iterations 251-260, 300, 450, 500, and 1000.

---

Figure 4: Effect of Activists with High Resistance (a/b = 1/2)

[Protest Levels]

---

---

Figure 5: Grid Snapshots Illustrating Role of Activists

[iteration: 251]	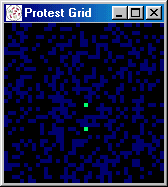[iteration: 252]	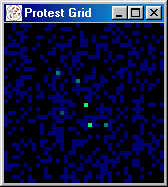[iteration: 253]
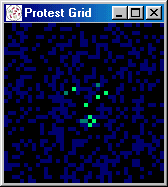[iteration: 254]	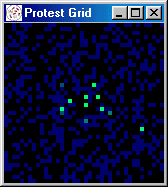[iteration: 255]	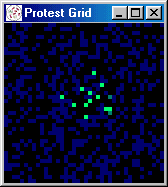[iteration: 256]
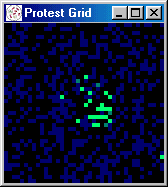[iteration: 257]	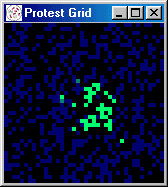[iteration: 258]	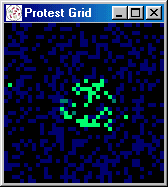[iteration: 259]

---

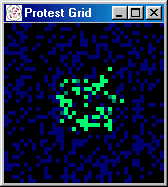Figure 6: Grid of Snapshots Illustrating Role of Activists (cont)

[iteration: 260]	[iteration: 300]	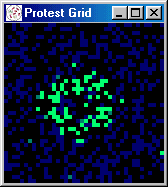[iteration: 450]
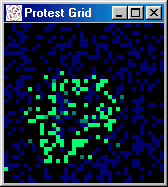[iteration: 500 ]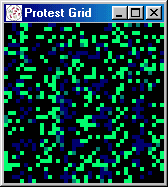	[iteration: 1000]

---

4.16

There are limits to what the activists can overcome, however. Raising the vision radius discourages the development of protest because the apparent probability of success remains low and the agents fail to respond to the activists. In Figures 7 and 8, we illustrate one run of the model in which the vision radius is raised to 7, while holding regime resistance at the already high value of 1/2. Again, we took snapshots of the grid at iteration 269. The run without activists is shown in Figure 7. In Figure 8, we illustrate the result of inserting 20 activists to the center cell. It has no apparent effect. This run is representative of a broader set of simulations.

---

Figure 7: High Vision Radius

[Protest Levels]

[Grid Snapshot]

---

Figure 8: Activists in a Model with High Vision Radius

[Protest Levels]

[Grid Snapshot]

---

Variability Across Model Runs

4.17

The level of observed protest depends on a complicated pattern of individual interactions. As such, one should expect that repetition of the model under a particular set of parameters will produce a variety of observed behaviors. Sometimes the protest movement coalesces at the beginning of the timeline, sometimes at the end, and sometimes never at all.

4.18

To convey a sense of the variability of results across runs, and to highlight the impact of activists on the observed level of unrest, we have collected the results of a final set of replications. We have fixed the vision radius of the agents at 7 and regime resistance at 1/2. We vary the population level between 4 and 1000, and assign three different values for the number activists: 0, 10, or 20. There are thus 250 runs of the model, one at each population level, for each of the three settings for the activists variable, resulting in a total of 750 runs. To summarize each simulation, we collected the average level and the maximum observed level of protest.

4.19

The scatterplots summarizing these results are presented in figures 9 and 10. Note that the observed levels of political unrest for low and medium population values are quite variable across runs. Random variations in the positioning of agents and the detailed sequencing of individual behaviors accounts for the observed variation.

4.20

Some additional points are worth emphasizing. Success-motivated protest movements do not materialize when the level of population density is high. When density is high, citizens can see many other citizens and they are never convinced that the level of existing protest is high enough to cause them to feel personal efficacy and join in. Random expressions of protest do not cause a bandwagon effect to commence. It is not likely that an agent will decide to protest simply because a few others are doing so. In order to generate self-sustaining levels of protest with these levels of population and vision, the level of regime resistance must be significantly lower.

4.21

In the middle ranges of population density, however, the addition of some activists can make a big difference some of the time. Note, for example, that when the population is 400, then the addition of 20 activists can cause high levels of unrest some of the time. With no activists protest means never exceed 5 percent at populations over 20; with twenty activists means of 10 percent or more are common if the population is no higher than 550. Protest maxima tell the same story, but do a better job of revealing the dampening effect of population.

---

Figure 9:

---

Figure 10:

---

Conclusion.

5.1

The purpose of this research project is to develop theory and explore its implications. The conditions of the simulation are simplified and abstracted to focus attention on a few key variables. We are motivated to pursue the S-shaped curve hypothesis and the importance of activists by some notable anecdotal accounts of protest movements, such as the events in Manila in 1986. We do not think the predictions of these simulation models will map one-for-one onto any particular historical sequence of events. Moreover, since one of the major points of emphasis has been the unpredictable nature of individual interaction which drives political protest, we think it would be inappropriate to try to make such an empirical stretch.

5.2

Our simulation results show that when the probability of favorable government response is in a middle range, a few consistent activists can make the difference in a society of success-motivated individuals. We discussed a number of parameters in the agent-based model that can make the recipe ``just so.'' The effects of key parameters such as regime resistance, vision, and population are nonlinear and highly interactive, but they contribute to dynamics that provide a simple explanation for when activists make a difference and when they will have no effect.

5.3

Success-motivated individuals will contribute to success only when their effort can be expected to matter. Sometimes the individuals can see too many others, or the regime is too resistant to change, and individuals who do see a few protesters will conclude that their own effort would be wasted in a losing cause. Under such conditions, a few activists can make a big difference. But their power to overcome perceptions of hopelessness is not without limits.

5.4

As a final contribution and spur to further research, our study invites investigation of situations where success-motivated collective action is stymied by an overly responsive regime. The idea that raising the probability of success can cause collective action to grow is well-established (e.g. Przeworski 1991, 3-4). This frequently occurred in our simulations. But what about the opposite dynamic? Are there situations where reducing regime responsiveness actually increases collective action? Do religious or environmental groups experience easier recruitment during the ascendancy of their political opponents, for example? Our study predicts that, at least some of the time, they should do so.

References