Sujai Kumar and Sugata Mitra (2006)
Self-Organizing Traffic at a Malfunctioning Intersection
Journal of Artificial Societies and Social Simulation
vol. 9, no. 4
<https://www.jasss.org/9/4/3.html>
For information about citing this article, click here
Received: 07-Mar-2006 Accepted: 07-Jul-2006 Published: 31-Oct-2006
 Abstract
AbstractIn many social situations, decisions made by individuals lead to external effects that may be very regular, even without a global coordinator. In traffic, these decisions concern when to accelerate or brake, to overtake or to enter a busy multi-lane road, while trying to get ahead as fast as possible, but safely, under the constraints imposed by physical limitations and traffic rules. At times these behaviours give rise to very regular traffic patterns, as exemplified by the universal characteristics of moving traffic-jam fronts or synchronized congested traffic. These phenomena are in contrast with usual social dilemmas, where cooperation in order to achieve a desirable collective behaviour hinges on having small groups or long time horizons.

|

|
| Figure 1. a) Overview of intersection, showing traffic flows, unsimulated lanes, and how vehicles wait at, and cross the intersection. b) The same intersection, as seen on Google Earth (download placemark at http://www.ylog.org/complex/traffic/kumar-mitra-selforg-traffic-malfunctioning-intersection.kml) | |

|
| Figure 2. Close-up of intersection, showing distance travelled by a vehicle when moving straight or turning across the intersection |

|
| Figure 3. Close-up of intersection. The darker colours show patches in the intersection which are either at a traffic light, or are crossed by more than one traffic flow |

|
| Figure 4. signal-type: Normal; signal-cycle-time: 60 time-steps; car-density: 1.0, wait-time-limit 60 time-steps |

|
| Figure 5. signal-type: Normal; signal-cycle-time: 60 time-steps; car-density: 1.0. Same parameters as Fig. 4, except that the plot window is 60 time-steps instead of 20 |

|
| Figure 6. signal-type: Normal; signal-cycle-time: 120 time-steps; car-density: 1.0. Same parameters as in Fig. 4, with the signal-cycle-time doubled |
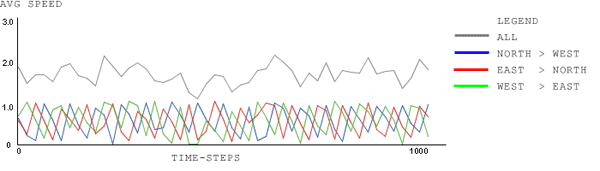
|
| Figure 7. signal-type: Normal; signal-cycle-time: 60 time-steps; car-density: 0.1. Same parameters as in Fig. 4, with the car-density reduced |

|
| Figure 8. Gridlock configuration with no further movement possible |

|
| Figure 9. signal-type: Normal; wait-time-limit: 40 time-steps; signal-cycle-time: 180; car-density: 1.0 |

|
| Figure 10. signal-type: Normal; wait-time-limit: 55 time-steps; signal-cycle-time: 180; car-density: 1.0; plot-window: 60 time-steps |

|
| Figure 11. signal-type: North-Green, Rest Red; wait-time-limit: 120 time-steps; car-density: 1.0, plot-window: 40 time-steps; signal-cycle-time is immaterial as this is a malfunctioning signal |

|
| Figure 12. signal-type: North-Green, Rest Red; wait-time-limit: 120 time-steps; car-density: 1.0, plot-window: 40 time-steps; 2000 to 4000 time-steps |

|
| Figure 13. signal-type: North-Green, Rest Red; wait-time-limit: 120 time-steps; car-density: 1.0, plot-window: 40 time-steps; 4000 to 6000 time-steps |

|
| Figure 14. Proportion of runs that ended in gridlock for differing wait-time-limits, for signal-type: "North-Green, Rest Red", and traffic density 1.0 |
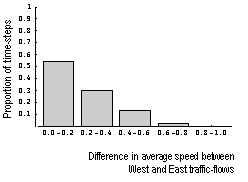
|
| Figure 15. Distribution of absolute differences in average speed for East and West traffic flows, for each time-step, across 100 runs, with wait-time-limit 120 time-steps |
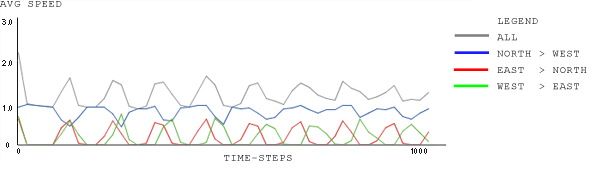
|
| Figure 16. signal-type: North-Green, Rest Red; wait-time-limit: 90 time-steps; car-density: 1.0 |

|
| Figure 17. signal-type: North-Green, Rest Red; wait-time-limit: 30 time-steps; car-density: 1.0 |

|
| Figure 18. signal-type: All-Green; wait-time-limit: 120 time-steps; car-density: 1.0, plot-window: 20 time-steps |

|
| Figure 19. signal-type: Stop rule; wait-time-limit: 120 time-steps; car-density: 1.0, plot-window: 20 time-steps |

|
| Table 1. Comparisons between three signal-types |
One possible limitation of the model is that each vehicle is physically too simple — it does not even account for varying vehicle velocities. In addition, all vehicles have exactly the same size. Varying these physical aspects of the vehicles could have an interesting effect on how often jams and gridlocks occur and how fast they dissolve. For example, different sized vehicles might cause gridlocks because smaller vehicles might fill the gaps between larger vehicles and prevent any further movement. On the other hand, smaller vehicles might be able to better utilize small gaps in order to escape a jam, and thus contribute to clearing the gridlock.
An infinite range of behavioural variations is possible. We have only considered one kind of behaviour where lawless drivers jump traffic lights when their vehicles stay stopped for a time-period longer than their wait-time-limit.
One behaviour that is often observed around the world but not accounted for in this model is the tendency for vehicles to change lanes when confronted with congestion in their own lane, or to change direction altogether and choose a different route.
Following the terminology of the classic Prisoner's Dilemma, drivers in India sometimes even switch to the lane going in the opposite direction because they want the immediate benefit of 'defecting', without appreciating the cumulative long-term effect of 'cooperating' with other vehicles.
Such behaviours would be interesting to model but it is difficult to see how they would lead to self-organizing behaviour.
Our simulation is only applicable to a three-way intersection where the traffic lights might freeze in a particular configuration. However, modelling other breakdown or malfunctioning situations — such as lane closures on a narrow mountain road, or the complete absence of traffic signals at a large intersection, could throw up some interesting insights as well into whether traffic might be able to flow efficiently in those cases as well in the absence of a regulatory system.
CAMAZINE, S., Deneubourg, J. L., Franks, N., Sneyd, J., Theraulaz, G., & Bonabeau, E. (2001) Self-organization in biological systems. Princeton University Press.
FEWELL, J. H. (2003). Social insect networks. Science, 301:1867-1870.
GERSHENSON, C. (2005). Self-organizing traffic lights. Complex Systems, 16(1): 29-53
GERSHENSON, C. and Heylighen, F. (2003) When can we call a system self-organizing? In Banzhaf, W., Christaller, T., Dittrich, P., Kim, J. T., & Ziegler, J. (eds), Advances in Artificial Life, 7th European Conference, ECAL 2003, Dortmund, Germany. pp. 606-614. Springer.
HELBING D and Schreckenberg M (1999) Cellular automata simulating experimental properties of traffic flow. Physical Review E, 59:2505-2508.
HELBING D. (2001) Traffic and related self-driven many-particle systems. Review of Modern Physics, 73(4):1067-1141.
HELBING, D. and HUBERMAN, B. (1998). Coherent moving states in highway traffic. Nature, 396:738-740.
HERRMANN M. and Kerner B. S. (1998) Generalized force model of traffic dynamics. Physica A, 255:163-188.
HOOGENDOORN, S. P. and Daamen, W (2004). Self-organization in walker experiments. In Proceedings Traffic and Granular Flow Conference (to be published).
KAUFFMAN, S. (1993). Origins of order: Self-organization and selection in evolution. Oxford University Press.
KOSHI M., Iwasaki M., Ohkura I. (1983) Some findings and overview on vehicle flow characteristics. In Hurdle V. F. et. al (eds.), Proceedings of 8th International Symposium on Transportation and Traffic Theory, (University of Toronto Press, Toronto, Ontario). p. 403.
KUMAR S. (2006) NetLogo simulation of self-organizing traffic at a malfunctioning intersection. Centre for Research in Cognitive Systems, retrieved 27 February 2006, http://ylog.org/complex/traffic/sot-2006-07-01-1930.html
LIGHTHILL M. J. and Whitham G. B. (1955) On Kinematic Waves. II. A theory of traffic flow on long crowded roads. Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences, 229(1178):317-345.
NAGATANI, T. (2002) The physics of traffic jams. Reports on Progress in Physics, 65:1331-1386.
NAGEL K. and Schreckenberg M. (1992) A cellular automaton model for freeway traffic. J. Phys. I France, 2:2221-2229.
SPALL, J. C. and Chin, D. C. (1997), Traffic-responsive signal timing for system-wide traffic control. Transportation Research, Part C, 5:153-163.
TREIBER, M. Helbing, D. (2001) Microsimulations of freeway traffic including control measures. Automatisierungstechnik, 49:478-484.
WILENSKY U. (1999) NetLogo. Center for Connected Learning and Computer-Based Modeling, NorthEastern University, Evanston, IL, retrieved 27 February 2006, http://ccl.northwestern.edu/netlogo/.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2006]